华为OD机考算法题:数字加减游戏
目录
题目部分
解读与分析
代码实现
题目部分
| 题目 | 数字加减游戏 |
| 难度 | 难 |
| 题目说明 | 小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字 s 变成数字 t 。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减,分别为 a, b (a≠b),其中 b 没有使用次数限制。 请问小明最少可以用多少次 a,才能将数字 s 变成数字 t 。 题目保证数字 s 一定能变成数字 t。 |
| 输入描述 | 输入的唯一一行包含四个正整数s,t,a,b(1≤s,t,a,b≤ |
| 输出描述 | 输出的唯一一行包含一个整数,表示最少需要使用多少次 a 才能将数字 s 变成数字 t。 |
| 补充说明 | 无 |
| ------------------------------------------------------ | |
| 示例 | |
| 示例1 | |
| 输入 | 1 10 5 2 |
| 输出 | 1 |
| 说明 | 初始值 1 加一次 a 变成 6,然后加两次 b 变成 10,因此 a 的使用次数为 1。 |
| 示例2 | |
| 输入 | 11 33 4 10 |
| 输出 | 2 |
| 说明 | 11 减两次 a 变成 3,然后加三次 b 变成 33,因此 a 的使用次数为 2 次。 |
解读与分析
题目解读:
由于 a 加一次后再减一次等于 0,在这里需要计算最少次数,所以我们不必做既加又减的操作。同时,也假设 b 也只做一种操作,也不存在既加又减的情况。
在这个前提下,此题要求在 s 的基础上,加减若干次 a,再加减若干次 b,最后得到 t。
本质上,由 s 变成 t ,与 由 t 变成 s相比,加减 a 、b 的次数是一样的,无非就是逆向操作,加变减,减变加。
更进一步思考,s 变成 t,与 ( s + 1) 变成 ( t + 1 ) 也是一样的,其实就是发生 | s - t | 差值的变化。
分析与思路:
由于 s、t 是固定值,我们假设 n = | s - t |。
此题可以转变为:一个原始数据,加或减a 若干次(假设为 x),加或减 b 若干次(假设为 y),产生的变化为 n 。
此题有 3 种情况:
1. a * x - b * y = n
2. b * y - a * x = n
3. a * x + b * y = n
其中,x、y 均为正整数。
这 3 个等式可以做如下转换。
1. a * x - b * y = n y =
2. b * y - a * x = n y =
3. a * x + b * y = n y =
其中, 第 1 个 和 第 3 个 可以合并成 y = 。
在 y = 和 y =
这两个等式中,它们的分母都能被 b 整除,这意味着这两个等式可以转换成:
1. ( a * x ) % b = n % b
2. ( a * x ) % b = ( b - n % b) % b
这两个等式的右边都是常数。此题进一步简化:找出最小的 x,使其满足以上 2 个条件中的任意一个。
x 的取值范围是多少呢?由于等式对 b 进行取模操作,即意味着当 x == 0 等同于 x == b, x == 1 也等同于 x == ( b + 1)。直观地看, x 的取值范围为 0 ≤ x < b。
更进一步,假设 a、b 的最小公倍数是 L,那么 a 加 次与 b 加
次是相等的,因此 x 的取值范围可以进一步缩小到 0 ≤ x <
。
那么,此题就可以简化成,把 x 从 0 到 ,代入到等式
1. ( a * x ) % b = n % b
2. ( a * x ) % b = ( b - n % b) % b
中,当这两个等式中任意一个成立时,x 的值即是最小的值。
题目中提到,“题目保证数字 s 一定能变成数字 t”,那我们在遍历时,无需去计算 的值,必定会在
之前求出 x 的值。
更进一步,先求 a 与 b 的最大公约数(设为 C1),再求 n 与 b 的最大公约数(C2),接着求 C1 和 C2 的最大公约数(设为 C),那么等式就变成了:
1. ( * x ) %
=
%
2. ( * x ) %
= (
-
%
) %
此时, 与
的最小公倍数变为原来的
,x 的范围进一步缩小。
但是,写代码的时候完全不必关心这些。尽管 x 的取值范围进一步缩小,x 的值不会发生改变,从 0 开始遍历,遍历的次数仍旧不会发生改变。
此题空间复杂度为 o(1)。由于输入数字最大不超过10的5次方,运行时间很短。
代码实现
Java代码
import java.util.Scanner;/*** 数字加减游戏* * @since 2023.09.08* @version 0.1* @author Frank**/
public class NumPlusMinusGame {public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {String input = sc.nextLine();String[] numbers = input.split( " " );processNumPlusMinusGame( numbers );}}private static void processNumPlusMinusGame( String numbers[] ){int s = Integer.parseInt( numbers[0] );int t = Integer.parseInt( numbers[1] );int a = Integer.parseInt( numbers[2] );int b = Integer.parseInt( numbers[3] );int n = Math.abs( s - t );// 当modValue1 可能等于 modValue2,如 modValue1 等于0 或 等于 b/2 的情况。int modValue1 = n % b;int modValue2 = ( b - n % b ) % b;int i = 0;while( true ){int tmpModValue = ( a * i ) % b;if( tmpModValue == modValue1 || tmpModValue == modValue2 ){System.out.println(i);return;}i ++;}}
}JavaScript代码
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;
void async function() {while (line = await readline()) {var numberArr = line.split(" ");processNumPlusMinusGame(numberArr);}}();function processNumPlusMinusGame(numberArr) {var s = parseInt(numberArr[0]);var t = parseInt(numberArr[1]);var a = parseInt(numberArr[2]);var b = parseInt(numberArr[3]);var n = Math.abs(s - t);// 当modValue1 可能等于 modValue2,如 modValue1 等于0 或 等于 b/2 的情况。var modValue1 = n % b;var modValue2 = (b - n % b) % b;var i = 0;while (true) {var tmpModValue = (a * i) % b;if (tmpModValue == modValue1 || tmpModValue == modValue2) {console.log(i);return;}i++;}}(完)
相关文章:
华为OD机考算法题:数字加减游戏
目录 题目部分 解读与分析 代码实现 题目部分 题目数字加减游戏难度难题目说明小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字 s 变成数字 t 。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减…...

WPF命令
在设计良好的Windows应用程序中,应用程序逻辑不应位于事件处理程序中,而应在更高层的方法中编写代码。其中的每个方法都代表单独的应用程序任务。每个任务可能依赖其他库。 使用这种设计最明显的方式是在需要的地方添加事件处理程序,并使用各…...
Unity中Shader的屏幕抓取 GrabPass
文章目录 前言一、抓取1、抓取指令2、在使用抓取的屏幕前,需要像使用属性一样定义一下,_GrabTexture这个名字是Unity定义好的 前言 Unity中Shader的屏幕抓取 GrabPass 一、抓取 1、抓取指令 屏幕的抓取需要使用一个Pass GrabPass{} GrabPass{“NAME”} 2、在使用…...
手撕 队列
队列的基本概念 只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 队列用链表实现 队列的实现 队列的定义 队列…...
【autodl/linux配环境心得:conda/本地配cuda,cudnn及pytorch心得】-未完成
linux配环境心得:conda/本地配cuda,cudnn及pytorch心得 我们服务器遇到的大多数找不到包的问题一,服务器安装cuda和cudnn使用conda在线安装cuda和cudnn使用conda进行本地安装检查conda安装的cuda和cudnn本地直接安装cuda和cudnn方法一&#x…...
macOS Ventura 13.5.2(22G91)发布,附黑/白苹果镜像下载地址
系统介绍(下载请百度搜索:黑果魏叔) 黑果魏叔 9 月 8 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.5.2 更新(内部版本号:22G91),本次更新距离上次发布隔了 21 天。 本次更新查…...

vue 子组件向父组件传递参数 子传父
子组件中写: this.$emit(RowCount,res.data.RowCount); 父组件中写: getMFGLRowCount(val){ //父组件中的方法: 接收子组件传过来的参数值赋值给父组件的变量 //this.totalCount val; alert("这…...

自然语言处理学习笔记(八)———— 准确率
目录 1.准确率定义 2.混淆矩阵与TP/FN/FP/TN 3. 精确率 4.召回率 5.F1值 6.中文分词的P、R、F1计算 7.实现 1.准确率定义 准确率是用来衡量一个系统的准确程度的值,可以理解为一系列评测指标。当预测与答案的数量相等时,准确率指的是系统做出正确判…...
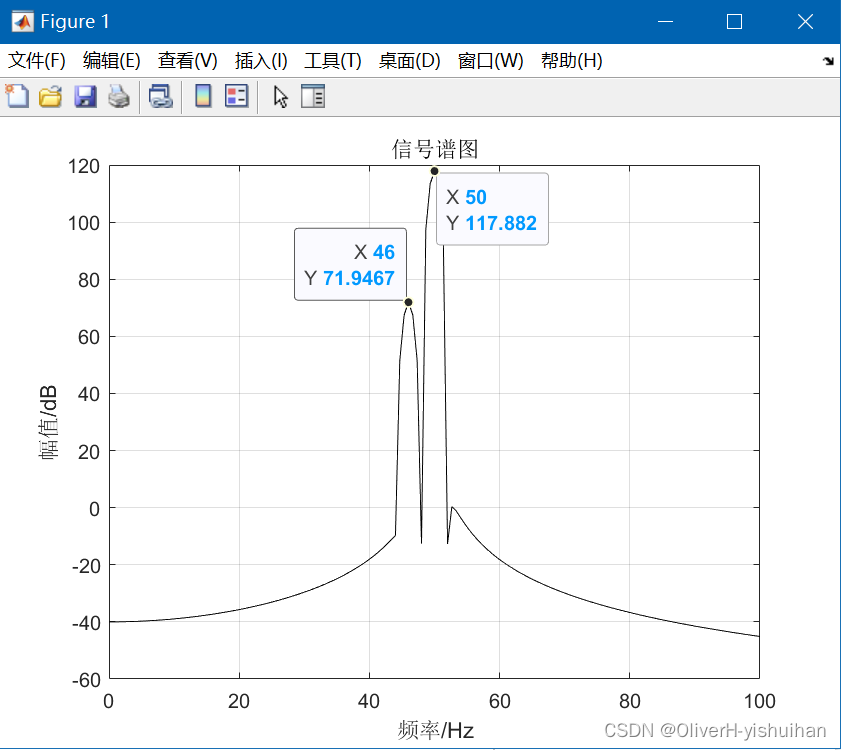
Matlab 如何选择窗函数和 FFT 的长度
Matlab 如何选择窗函数和 FFT 的长度 1、常用的四种窗函数 对于实际信号序列,如何选取窗函数呢?一般来说,选择第一旁瓣衰减大,旁瓣峰值衰减快的窗函数有利于緩解截断过程中产生的頻泄漏问题。但具有这两个特性的窗函数࿰…...

node.js下载安装环境配置以及快速使用
目录 一、下载 二、安装 三、测试安装是否成功 四、配置环境 五、测试配置环境是否成功 六、安装淘宝镜像 七、快速上手 1、建立一个自己的工作目录 2、下载工作代码 八、各种配置文件匹配问题入坑 九、总结 一、下载 Node.js 中文网 想选择其他版本或者其他系统使用…...
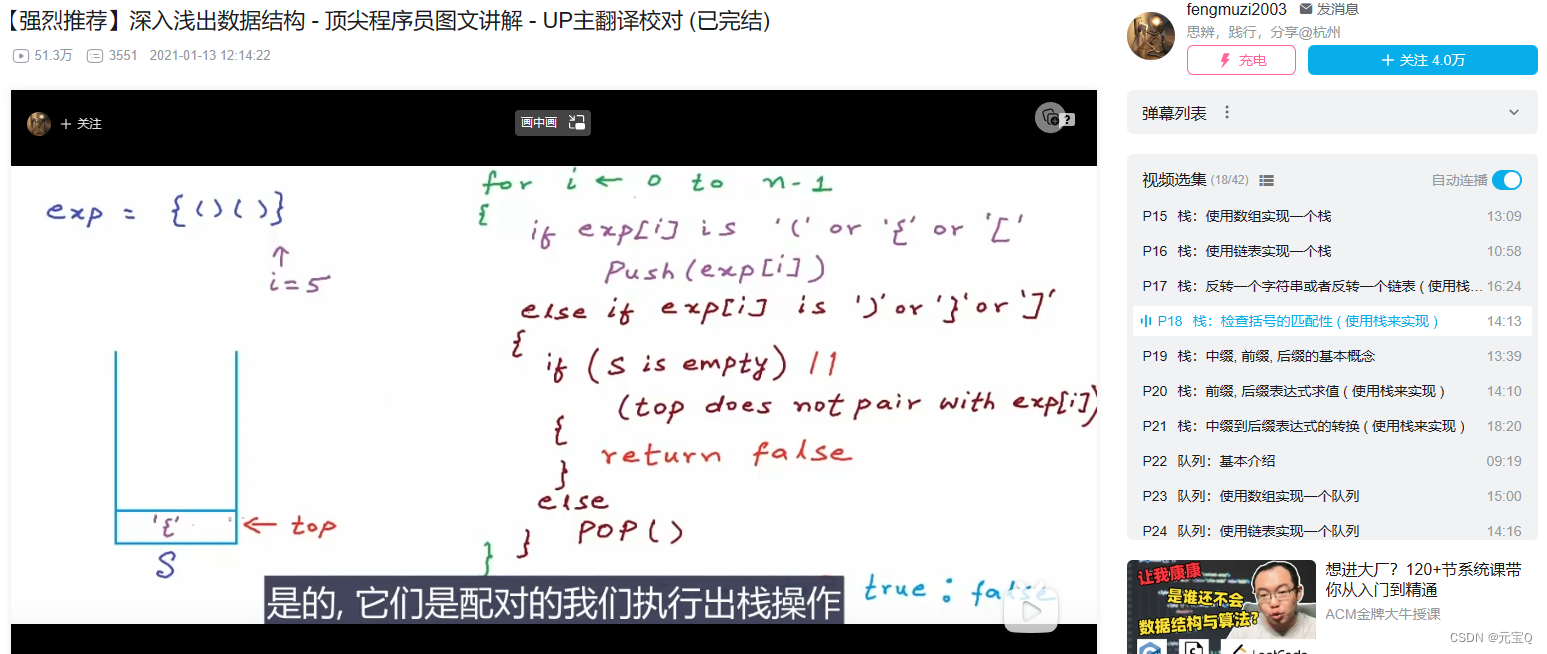
使用栈检查括号的合法性 C 实现
使用栈检查括号的合法性 思路讲解:首先从数组数组0下标开始,如果是左括号直接无脑压入栈,直到出现右括号开始判断合法与否。遇到右括号分两种情况,第一种是空栈的情况,也就是说我们第一个字符就是右括号,那…...

小白备战大厂算法笔试(四)——哈希表
文章目录 哈希表常用操作简单实现冲突与扩容链式地址开放寻址线性探测多次哈希 哈希表 哈希表,又称散列表,其通过建立键 key 与值 value 之间的映射,实现高效的元素查询。具体而言,我们向哈希表输入一个键 key ,则可以…...

云原生Kubernetes:pod基础
目录 一、理论 1.pod 2.pod容器分类 3.镜像拉取策略(image PullPolicy) 二、实验 1.Pod容器的分类 2.镜像拉取策略 三、问题 1.apiVersion 报错 2.pod v1版本资源未注册 3.取行显示指定pod信息 四、总结 一、理论 1.pod (1) 概念 Pod是ku…...
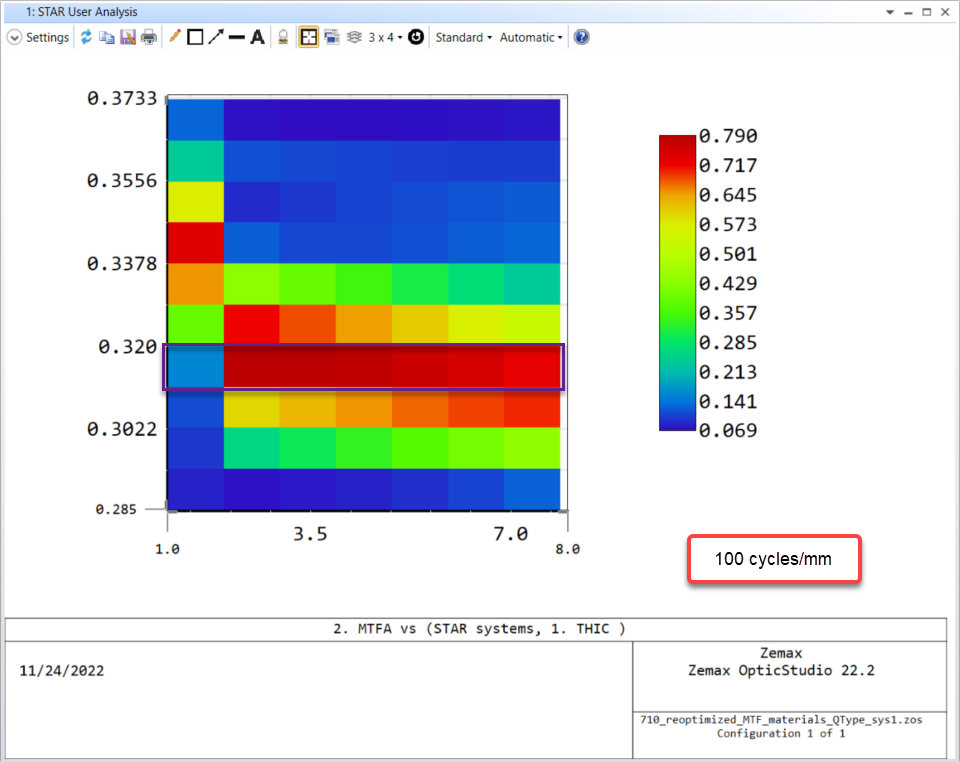
Ansys Zemax | 手机镜头设计 - 第 3 部分:使用 STAR 模块和 ZOS-API 进行 STOP 分析
本文是 3 篇系列文章的一部分,该系列文章将讨论智能手机镜头模组设计的挑战,从概念、设计到制造和结构变形的分析。本文是三部分系列的第三部分。它涵盖了使用 Ansys Zemax OpticStudio Enterprise 版本提供的 STAR 技术对智能手机镜头进行自动的结构、热…...

CSP-J初赛复习大题整理笔记
本篇全是整理,为比赛准备. 在这里插入代码片 #include<cstdio> using namespace std; int n, m; int a[100], b[100];int main() {scanf_s("%d%d", &n, &m);for (int i 1; i < n; i)a[i] b[i] 0;//将两个数组清0,这…...
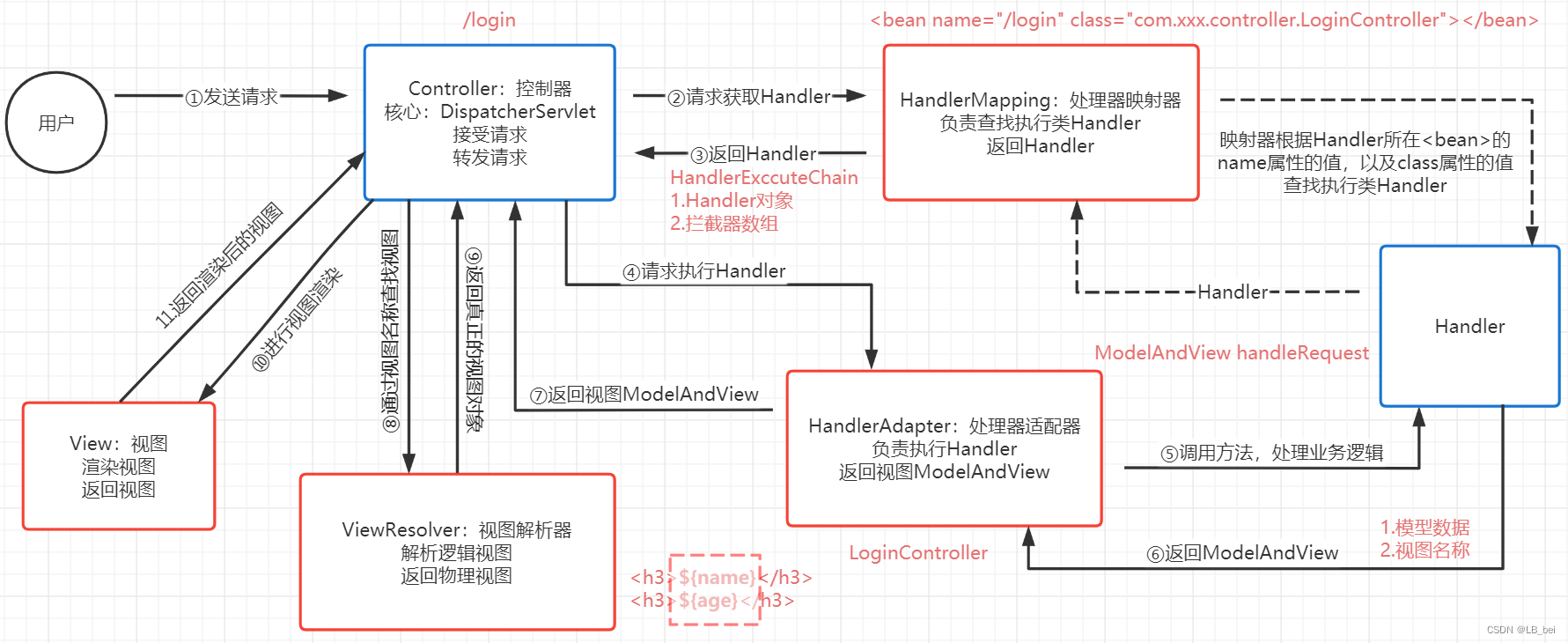
面试题 ⑤
1、TCP与UDP的区别 UDPTCP是否连接无连接,即刻传输面向连接,三次握手是否可靠不可靠传输,网络波动拥堵也不会减缓传输可靠传输,使用流量控制和拥塞控制连接对象个数支持一对一,一对多,多对一和多对多交互通…...

硅谷课堂1
文章目录 P1 项目概述P2—P12 MybatisPlus知识回顾P8 MybatisPlus实现逻辑删除P9 QueryWrapper使用P14 项目后端模块介绍P15 项目后端环境搭建P50—P53 整合腾讯云对象存储1、整合腾讯2、腾讯云示例3、讲师头像上传-后端代码P54—P60 课堂分类管理1、课堂分类查询2、课程分类导…...

第6节-PhotoShop基础课程-认识选区
文章目录 前言1.认识选区1.选区原理1.普通选区2.高级选区 2.功能用途1.抠图2.修图3.调色 3.关键操作(手术与屠宰的区别)2.加选(shift 是快捷键)3.减选(Alt是快捷键)4.交集(2,3合起来…...

SQLServer如何获取客户端IP
SQLServer如何获取客户端IP 很多用户询问如何通过SQLServer获取客户端IP从而定位一些问题,比如链接泄露,其实主要是利用几个相关视图,如下给出一些SQL方便用户排查 当前链接 SELECT CONNECTIONPROPERTY(PROTOCOL_TYPE) AS PROTOCOL_TYPE,CO…...

爬虫数据清洗可视化实战-就业形势分析
基于采集和分析招聘网站的数据的芜湖就业形势的调查研究 一、引言 本报告旨在分析基于大数据的当地就业形势,并提供有关薪资、工作地点、经验要求、学历要求、公司行业、公司福利以及公司类型及规模的详细信息。该分析是通过网络爬虫技术对招聘网站的数据进行采集…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
