【蓝桥杯每日一题】前缀和算法

🍎 博客主页：🌙@披星戴月的贾维斯
🍎 欢迎关注：👍点赞🍃收藏🔥留言
🍇系列专栏：🌙 蓝桥杯
🌙我与杀戮之中绽放，亦如黎明的花朵🌙
🍉一起加油，去追寻、去成为更好的自己！
蓝桥杯倒计时 45天

提示：以下是本篇文章正文内容，下面案例可供参考

---

🍎、前缀和

🍉、前缀和的简单概念

前缀和算法分为一维和二维，一维前缀和可以很快速的求序列中某一段的和。而二维前缀和可以快速求一个矩阵中某个子矩阵的和。

一维前缀和的图解：

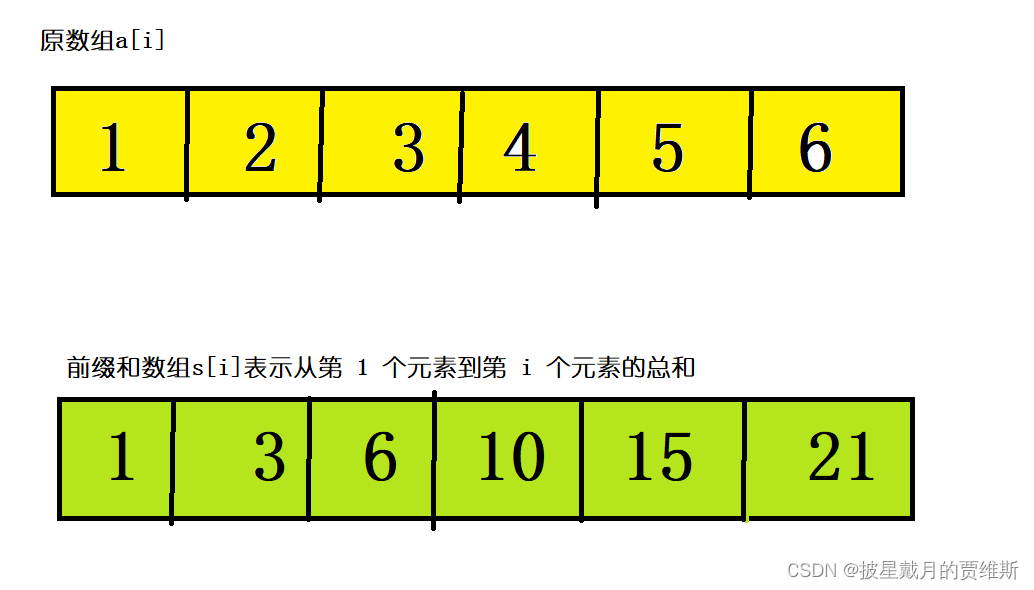
前缀和数组的计算方法：前缀和数组s[i]是由原数组a[i]递推而来的
即：s[i] = s[i - 1] + a[i]

🍎、例题分析

🍇、（AcWing）前缀和

分析题意：每次询问查询的是原数组l - r区间内的和， 因此我们可以设置一个原数组a和一个前缀和数组

代码示例：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010;
int a[N];//原数组
int s[N];//前缀合数组
int n, m;int main ()
{cin >> n >> m;for(int i = 1; i <= n; i++) {scanf("%d", &a[i]);s[i] = s[i - 1] + a[i];}while(m --){int l , r;cin >> l >> r;printf("%d\n", s[r] - s[l - 1]);}return 0;
}

解法2：因为本题不需要用到原数组a,则可以直接创建一个前缀和数组s,并且原数组a上 L - R 区间内的值就是前缀和数组 s[R] - s[L - 1];
代码示例：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int m, n;
int s[100010];
int main ()
{cin >> n >> m;for(int i = 1; i <= n; i++){scanf("%d", &s[i]);s[i] += s[i - 1];}while(m --){int ans = 0;int l, r;cin >> l >> r;ans = s[r] - s[l - 1];cout << ans << endl;}return 0;
}

🍇、（AcWing）子矩阵的和 二维前缀和

图解二维前缀和的公式


代码示例：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int a[N][N], s[N][N];
int n, m, q;
int main ()
{cin >> n >> m >> q;for(int i =  1; i <= n; i++)for(int j = 1; j <= m; j++){scanf("%d", &a[i][j]);s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];//计算二维前缀和}while(q --){int x1, x2, y1, y2;//计算每一次结果cin >> x1 >> y1 >> x2 >> y2;int ans = s[x2][y2] - s[x1 -1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 -1];cout << ans << endl;}return 0;
}

🍇、（AcWing）截断数组

算法：前缀和 + 枚举

**分析题意：枚举第二刀i处。

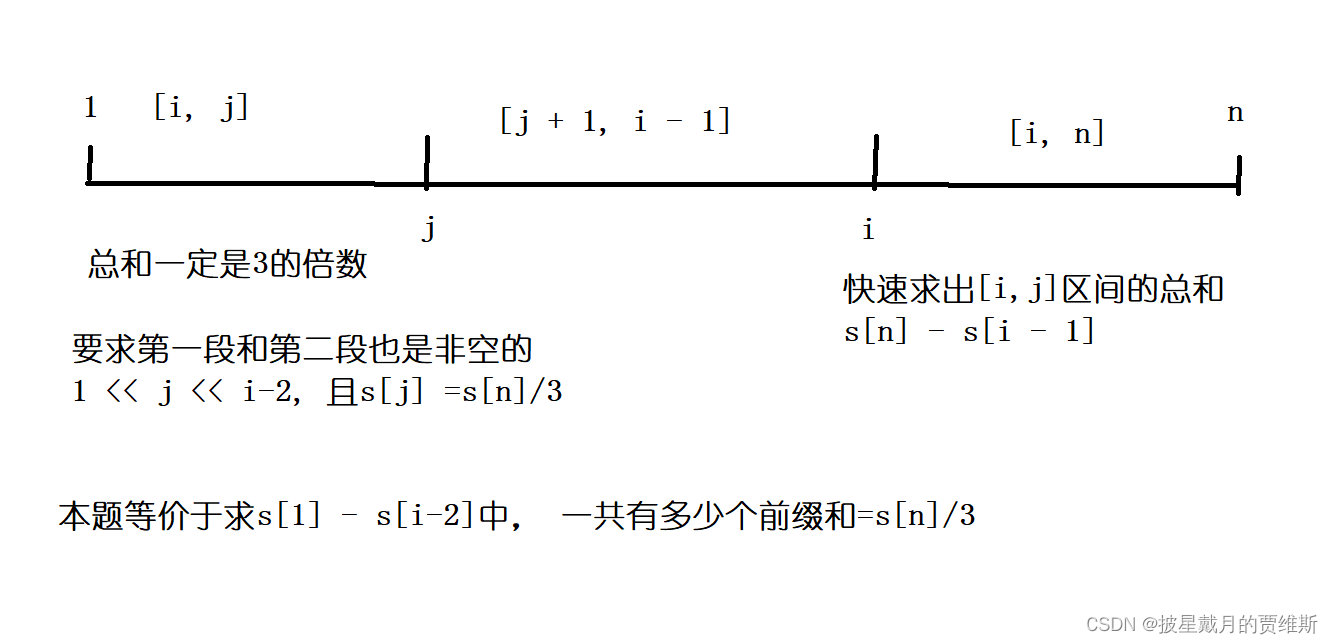
代码示例：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int s[N];
int main ()
{cin >> n;for(int i =1; i <= n; i++){int x;scanf("%d", &x);s[i] = s[i - 1]  + x; //处理前缀和数组s[i]}if(s[n] % 3) //提前判断结束条件{cout << "0" << endl;return 0;}LL res = 0;//因为答案可能爆intfor(int i = 3, cnt = 0; i <= n; i++){if(s[i - 2] == s[n] / 3) cnt++;if(s[n] - s[i - 1] == s[n] / 3) res += cnt; //s[n] - s[i - 1]是计算i - n区间的总和}printf("%lld\n", res);return 0;
}

---

🍎、总结

    本文简要介绍了前缀和的简要概念和几道前缀和的经典例题，希望大家读后能有所收获！