2023-9-8 求组合数(二)
题目链接:求组合数 II

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;
const int mod = 1e9 + 7;
const int N = 100010;// 阶乘,阶乘的逆
int fact[N], infact[N];LL qmi(int a, int k, int p)
{int res = 1;while(k){if(k & 1) res = (LL) res * a % p;a = (LL) a * a % p;k >>= 1;}return res;
}int main()
{fact[0] = infact[0] = 1;for(int i = 1; i < N; i++){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;}int n;cin >> n;while(n--){int a, b;cin >> a >> b;cout << (LL) fact[a] * infact[b] % mod * infact[a - b] % mod << endl;}return 0;
}
相关文章:

2023-9-8 求组合数(二)
题目链接:求组合数 II #include <iostream> #include <algorithm>using namespace std;typedef long long LL; const int mod 1e9 7; const int N 100010;// 阶乘,阶乘的逆 int fact[N], infact[N];LL qmi(int a, int k, int p) {int res…...

k8s service的一些特性
文章目录 Service分发负载的策略同一端口通过不同协议暴露Headless Service的负载分发策略 Service分发负载的策略 大家都知道,一个service可以对应多个pod,那么一定要有一些方法来把service接收到的请求(负载)转发到pod上。 一般…...

C++中std::enable_if和SFINAE介绍
作为一个标准的C++模板类,我们先看下enable_if的定义: // STRUCT TEMPLATE enable_if template <bool _Test, class _Ty = void> struct enable_if {}; // no member "type" when !_Testtemplate <class _Ty> struct enable_if<true, _Ty> { //…...
华为OD机考算法题:数字加减游戏
目录 题目部分 解读与分析 代码实现 题目部分 题目数字加减游戏难度难题目说明小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字 s 变成数字 t 。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减…...

WPF命令
在设计良好的Windows应用程序中,应用程序逻辑不应位于事件处理程序中,而应在更高层的方法中编写代码。其中的每个方法都代表单独的应用程序任务。每个任务可能依赖其他库。 使用这种设计最明显的方式是在需要的地方添加事件处理程序,并使用各…...
Unity中Shader的屏幕抓取 GrabPass
文章目录 前言一、抓取1、抓取指令2、在使用抓取的屏幕前,需要像使用属性一样定义一下,_GrabTexture这个名字是Unity定义好的 前言 Unity中Shader的屏幕抓取 GrabPass 一、抓取 1、抓取指令 屏幕的抓取需要使用一个Pass GrabPass{} GrabPass{“NAME”} 2、在使用…...
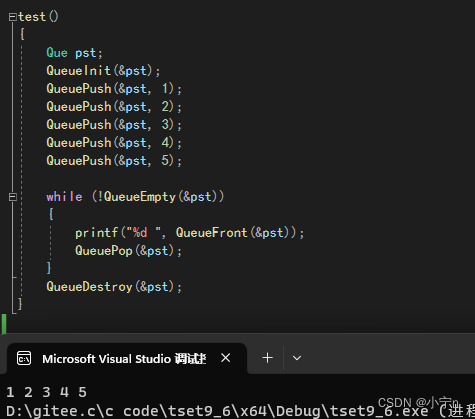
手撕 队列
队列的基本概念 只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 队列用链表实现 队列的实现 队列的定义 队列…...
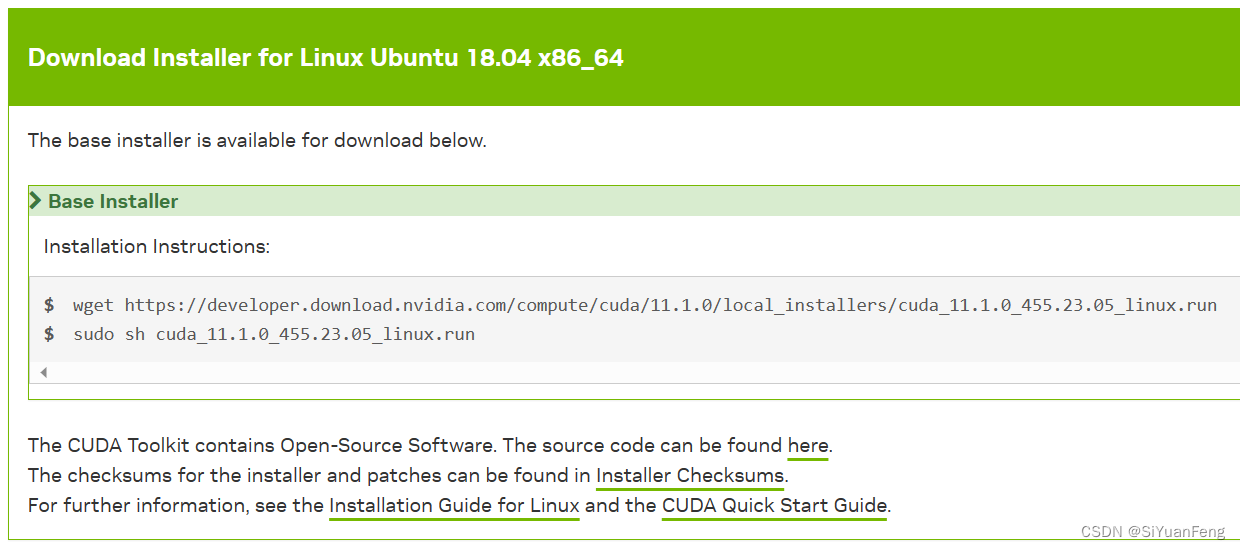
【autodl/linux配环境心得:conda/本地配cuda,cudnn及pytorch心得】-未完成
linux配环境心得:conda/本地配cuda,cudnn及pytorch心得 我们服务器遇到的大多数找不到包的问题一,服务器安装cuda和cudnn使用conda在线安装cuda和cudnn使用conda进行本地安装检查conda安装的cuda和cudnn本地直接安装cuda和cudnn方法一&#x…...
macOS Ventura 13.5.2(22G91)发布,附黑/白苹果镜像下载地址
系统介绍(下载请百度搜索:黑果魏叔) 黑果魏叔 9 月 8 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.5.2 更新(内部版本号:22G91),本次更新距离上次发布隔了 21 天。 本次更新查…...

vue 子组件向父组件传递参数 子传父
子组件中写: this.$emit(RowCount,res.data.RowCount); 父组件中写: getMFGLRowCount(val){ //父组件中的方法: 接收子组件传过来的参数值赋值给父组件的变量 //this.totalCount val; alert("这…...

自然语言处理学习笔记(八)———— 准确率
目录 1.准确率定义 2.混淆矩阵与TP/FN/FP/TN 3. 精确率 4.召回率 5.F1值 6.中文分词的P、R、F1计算 7.实现 1.准确率定义 准确率是用来衡量一个系统的准确程度的值,可以理解为一系列评测指标。当预测与答案的数量相等时,准确率指的是系统做出正确判…...
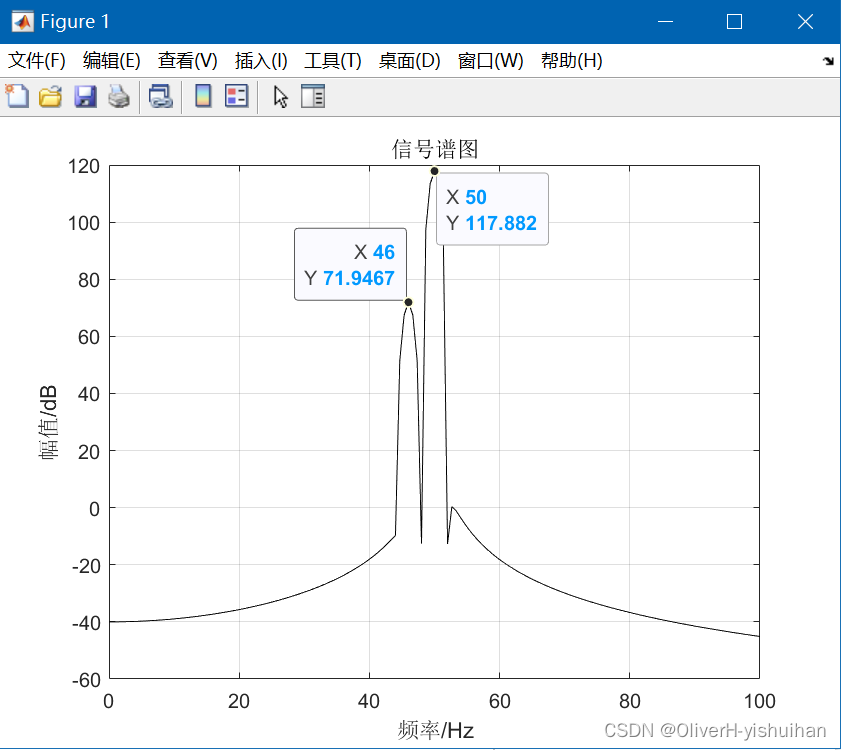
Matlab 如何选择窗函数和 FFT 的长度
Matlab 如何选择窗函数和 FFT 的长度 1、常用的四种窗函数 对于实际信号序列,如何选取窗函数呢?一般来说,选择第一旁瓣衰减大,旁瓣峰值衰减快的窗函数有利于緩解截断过程中产生的頻泄漏问题。但具有这两个特性的窗函数࿰…...

node.js下载安装环境配置以及快速使用
目录 一、下载 二、安装 三、测试安装是否成功 四、配置环境 五、测试配置环境是否成功 六、安装淘宝镜像 七、快速上手 1、建立一个自己的工作目录 2、下载工作代码 八、各种配置文件匹配问题入坑 九、总结 一、下载 Node.js 中文网 想选择其他版本或者其他系统使用…...
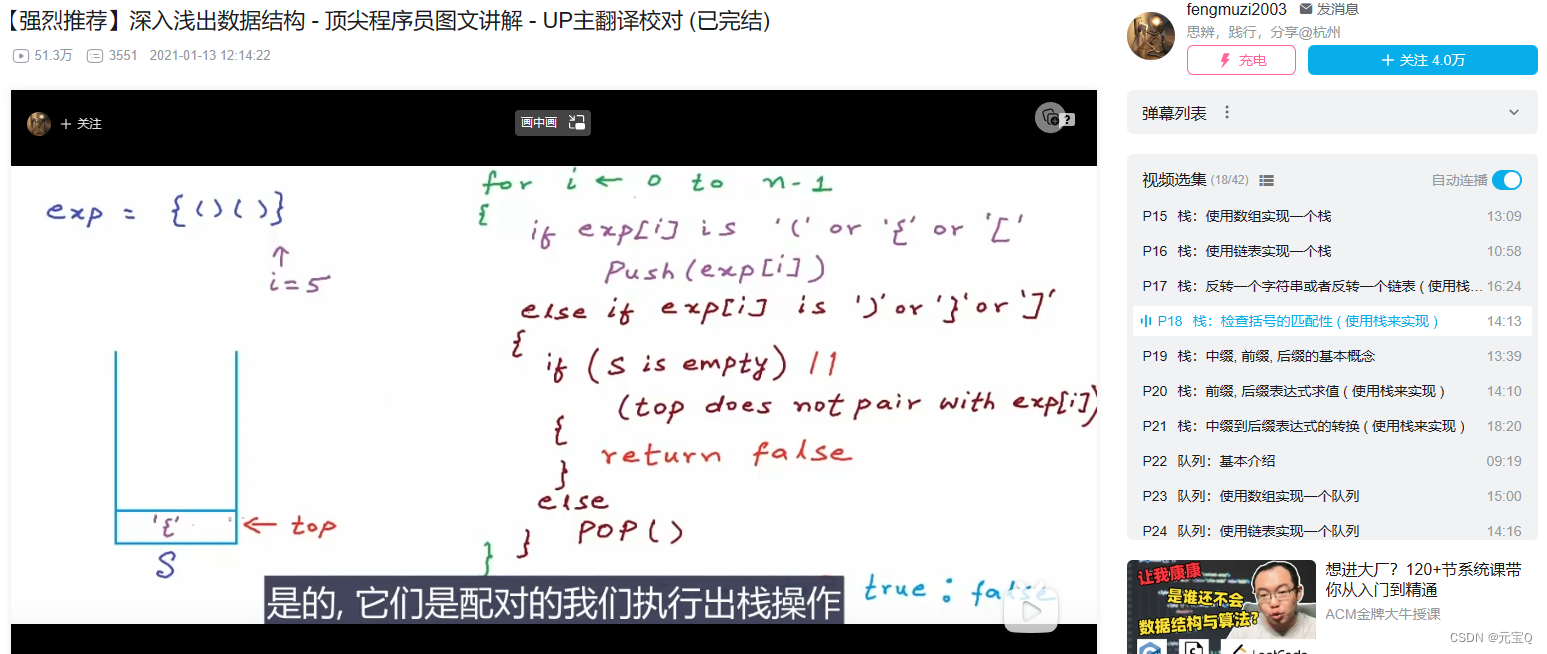
使用栈检查括号的合法性 C 实现
使用栈检查括号的合法性 思路讲解:首先从数组数组0下标开始,如果是左括号直接无脑压入栈,直到出现右括号开始判断合法与否。遇到右括号分两种情况,第一种是空栈的情况,也就是说我们第一个字符就是右括号,那…...

小白备战大厂算法笔试(四)——哈希表
文章目录 哈希表常用操作简单实现冲突与扩容链式地址开放寻址线性探测多次哈希 哈希表 哈希表,又称散列表,其通过建立键 key 与值 value 之间的映射,实现高效的元素查询。具体而言,我们向哈希表输入一个键 key ,则可以…...

云原生Kubernetes:pod基础
目录 一、理论 1.pod 2.pod容器分类 3.镜像拉取策略(image PullPolicy) 二、实验 1.Pod容器的分类 2.镜像拉取策略 三、问题 1.apiVersion 报错 2.pod v1版本资源未注册 3.取行显示指定pod信息 四、总结 一、理论 1.pod (1) 概念 Pod是ku…...
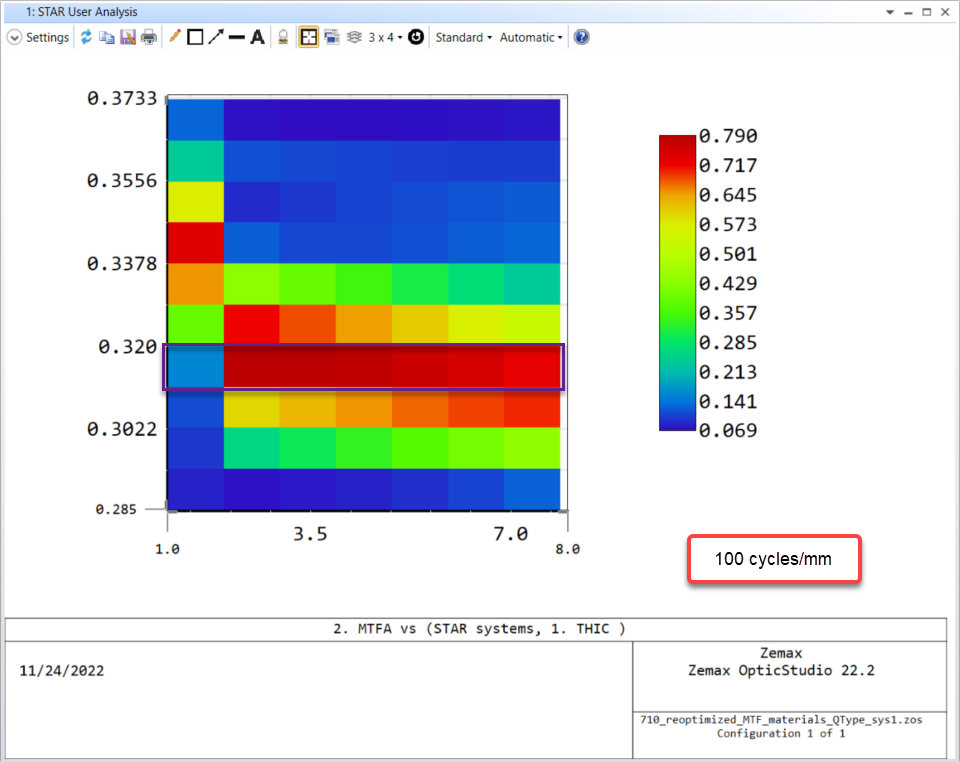
Ansys Zemax | 手机镜头设计 - 第 3 部分:使用 STAR 模块和 ZOS-API 进行 STOP 分析
本文是 3 篇系列文章的一部分,该系列文章将讨论智能手机镜头模组设计的挑战,从概念、设计到制造和结构变形的分析。本文是三部分系列的第三部分。它涵盖了使用 Ansys Zemax OpticStudio Enterprise 版本提供的 STAR 技术对智能手机镜头进行自动的结构、热…...

CSP-J初赛复习大题整理笔记
本篇全是整理,为比赛准备. 在这里插入代码片 #include<cstdio> using namespace std; int n, m; int a[100], b[100];int main() {scanf_s("%d%d", &n, &m);for (int i 1; i < n; i)a[i] b[i] 0;//将两个数组清0,这…...
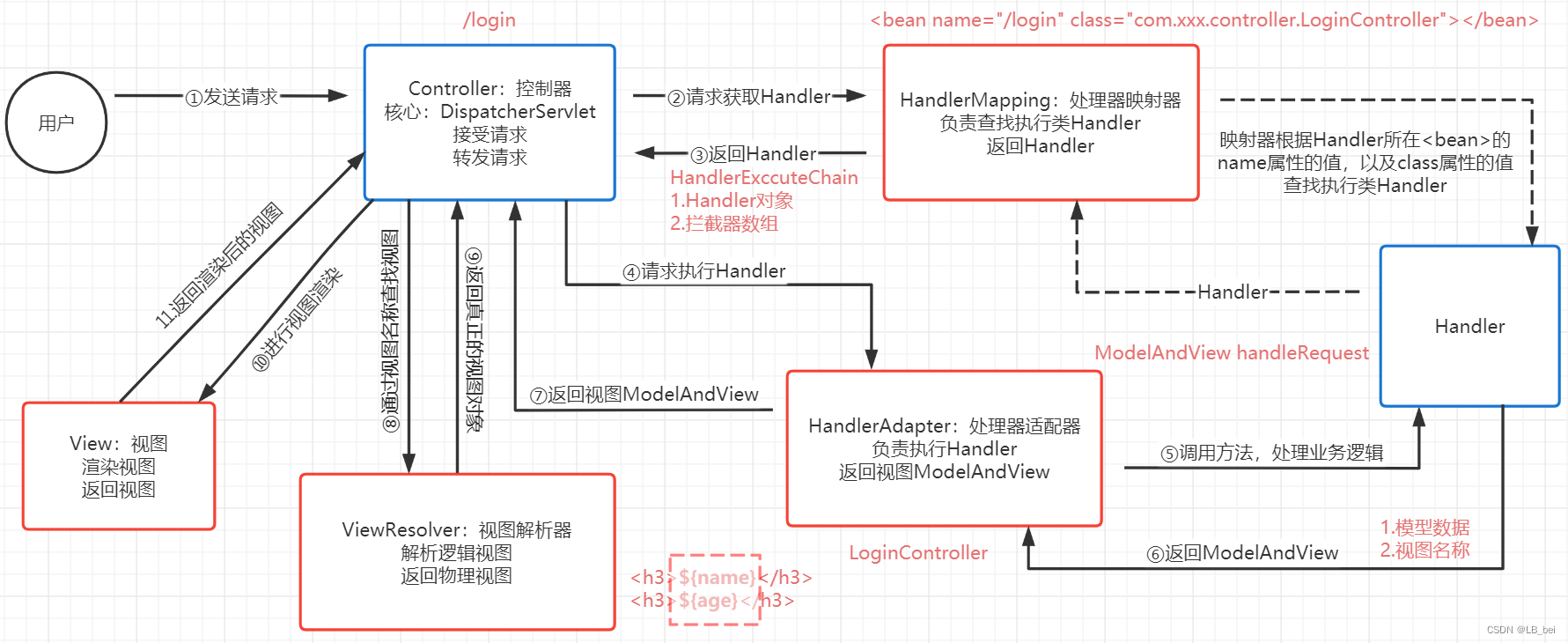
面试题 ⑤
1、TCP与UDP的区别 UDPTCP是否连接无连接,即刻传输面向连接,三次握手是否可靠不可靠传输,网络波动拥堵也不会减缓传输可靠传输,使用流量控制和拥塞控制连接对象个数支持一对一,一对多,多对一和多对多交互通…...

硅谷课堂1
文章目录 P1 项目概述P2—P12 MybatisPlus知识回顾P8 MybatisPlus实现逻辑删除P9 QueryWrapper使用P14 项目后端模块介绍P15 项目后端环境搭建P50—P53 整合腾讯云对象存储1、整合腾讯2、腾讯云示例3、讲师头像上传-后端代码P54—P60 课堂分类管理1、课堂分类查询2、课程分类导…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
