归并排序和快速排序的两种实现
在此之前我们已经介绍过归并排序和快速排序:浅谈归并排序与快速排序,但其中的实现都是基于递归的。本文将重新温故这两种算法并给出基于迭代的实现。
目录
- 1. 归并排序
- 1.1 基于递归
- 1.2 基于迭代
- 2. 快速排序
- 2.1 基于递归
- 2.2 基于迭代
1. 归并排序
1.1 基于递归
归并排序的核心是二路归并,实现二路归并需要一个额外的辅助数组,因此空间复杂度是 O ( n ) O(n) O(n)。
void merge(vector<int>& a, int l, int mid, int r, vector<int>& tmp) {int i = l, j = mid + 1, k = l;while (i <= mid && j <= r) {if (a[i] <= a[j]) tmp[k++] = a[i++];else tmp[k++] = a[j++];}while (i <= mid) tmp[k++] = a[i++];while (j <= r) tmp[k++] = a[j++];for (int i = l; i <= r; i++) a[i] = tmp[i];
}
该函数会对数组 a 的 [l, mid] 和 [mid + 1, r] 两部分进行二路归并,其中辅助数组 tmp 的大小与 a 相同。
有了 merge 函数,我们就可以很方便的实现归并排序了:
void merge_sort(vector<int>& a, int l, int r, vector<int>& tmp) {if (l >= r) return;int mid = l + r >> 1;merge_sort(a, l, mid, tmp), merge_sort(a, mid + 1, r, tmp);merge(a, l, mid, r, tmp);
}
1.2 基于迭代
很明显,基于递归的实现是自顶向下的,而基于迭代的实现是自底向上的。
我们可以先枚举区间长度,再枚举区间左端点。一开始每个区间的长度是 1 1 1,我们每次对相邻的两个区间进行二路归并,每归并一次区间的长度就是原先的两倍,所以枚举区间长度时变量 len 的更新方式为 len *= 2。
对于区间左端点,每合并完两个区间后,左端点就要更新成下下个区间,如下图所示:
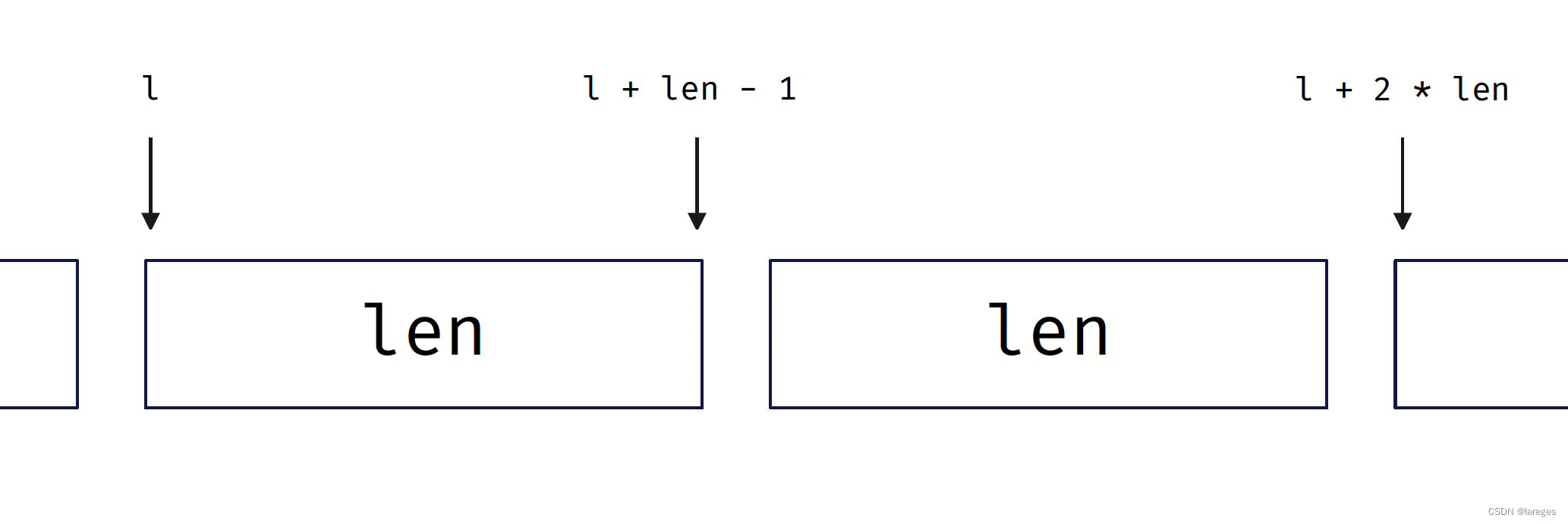
还需保证 mid < n - 1,即 l < n - len。
void merge_sort(vector<int>& a) {int n = a.size();vector<int> tmp(n);for (int len = 1; len < n; len *= 2) {for (int l = 0; l < n - len; l += 2 * len) {int mid = l + len - 1;int r = min(l + 2 * len - 1, n - 1);merge(a, l, mid, r, tmp);}}
}
归并排序的时间复杂度是 O ( n log n ) O(n\log n) O(nlogn),无论是递归还是迭代,空间复杂度都是 O ( n ) O(n) O(n)。
2. 快速排序
2.1 基于递归
void quick_sort(vector<int>& a, int l, int r) {if (l >= r) return;int mid = l + r >> 1;int i = l - 1, j = r + 1, x = a[mid];while (i < j) {while (a[++i] < x);while (a[--j] > x);if (i < j) swap(a[i], a[j]);}quick_sort(a, l, j), quick_sort(a, j + 1, r);
}
2.2 基于迭代
void quick_sort(vector<int>& a, int l, int r) {if (l >= r) return;stack<pair<int, int>> stk;stk.emplace(l, r);while (!stk.empty()) {auto [l, r] = stk.top();stk.pop();if (l < r) {int mid = l + r >> 1;int i = l - 1, j = r + 1, x = a[mid];while (i < j) {while (a[++i] < x);while (a[--j] > x);if (i < j) swap(a[i], a[j]);}stk.emplace(l, j);stk.emplace(j + 1, r);}}
}
时间复杂度是 O ( n log n ) O(n\log n) O(nlogn),空间复杂度是 O ( log n ) O(\log n) O(logn)。
相关文章:

归并排序和快速排序的两种实现
在此之前我们已经介绍过归并排序和快速排序:浅谈归并排序与快速排序,但其中的实现都是基于递归的。本文将重新温故这两种算法并给出基于迭代的实现。 目录 1. 归并排序1.1 基于递归1.2 基于迭代 2. 快速排序2.1 基于递归2.2 基于迭代 1. 归并排序 1.1 基…...

C#,《小白学程序》第十四课:随机数(Random)第一,几种随机数的计算方法与代码
1 文本格式 /// <summary> /// 《小白学程序》第十四课:随机数(Random)第一,几种随机数的计算方法与代码 /// 本课初步接触一下随机数。 /// </summary> /// <param name"sender"></param> ///…...

[杂谈]-快速了解Modbus协议
快速了解Modbus协议 文章目录 快速了解Modbus协议1、为何 Modbus 如此受欢迎2、范围和数据速率3、逻辑电平4、层数5、网络与通讯6、数据帧格式7、数据类型8、服务器如何存储数据9、总结 Modbus 是一种流行的低速串行通信协议,广泛应用于自动化行业。 该协议由 Mo…...
WhatsApp的两个商业模式该如何选择
WhatsApp Business 是什么 目前 WhatsApp 提供两种商业模式,企业应根据自身需求选择相应版本。 第一个版本是 WhatsApp Business:初创企业只需一个手机应用程序,便可以个体单位与客户轻松互动; 另一个版本是 WhatsApp Business APIÿ…...
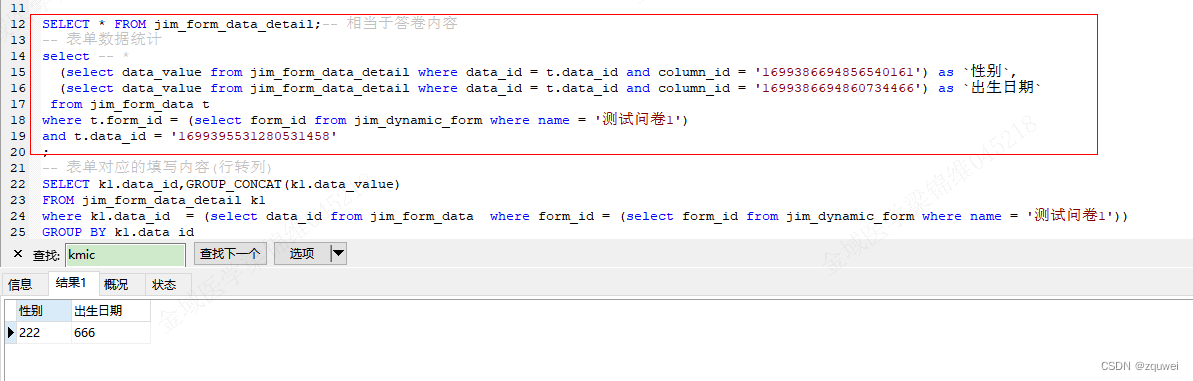
动态表单设计
动态表单设计 背景方案讨论基于上面分析,对比调研,自定义动态表单数据模型表单详解(一) 表单模板:jim_dynamic_form(二)表单数据类型:jim_form_data_type(三)…...

JAR will be empty - no content was marked for inclusion!
现象 在对自建pom依赖组件打包时,出现JAR will be empty - no content was marked for inclusion!错误。 方案 在pom中怎么加packaging标签内容为pom,标识只打包pom文件 <?xml version"1.0" encoding"UTF-8"?> ...<grou…...
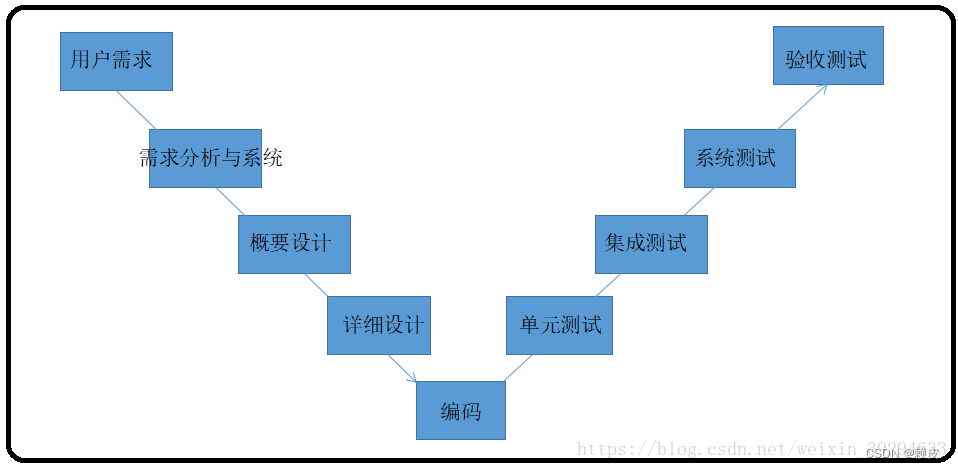
软件生命周期及流程【软件测试】
软件的生命周期 软件生命周期是软件开始研制到最终被废弃不用所经历的各个阶段。 瀑布型生命周期模型 规定了它们自上而下、相互衔接的固定次序,如同瀑布流水,逐级下落,具有顺序性和依赖性。每个阶段规定文档并需进行评审。 特点ÿ…...
2023高教社杯数学建模E题思路代码 - 黄河水沙监测数据分析
# 1 赛题 E 题 黄河水沙监测数据分析 黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变 化和人民生活的影响, 以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾 等方面都具有重要的理论指导意义。 附件 1 给出了位…...
双翌保养码使用指南方法(一)
保养码使用指南一 为了确保软件的正常运行和有效使用,正确地使用保养码是至关重要的。以下是保养码使用的简单指南,以帮助您进行正确的操作。 1. 打开软件入口:首先,在您的电脑上打开文件夹,并找到s-y softactive tool…...
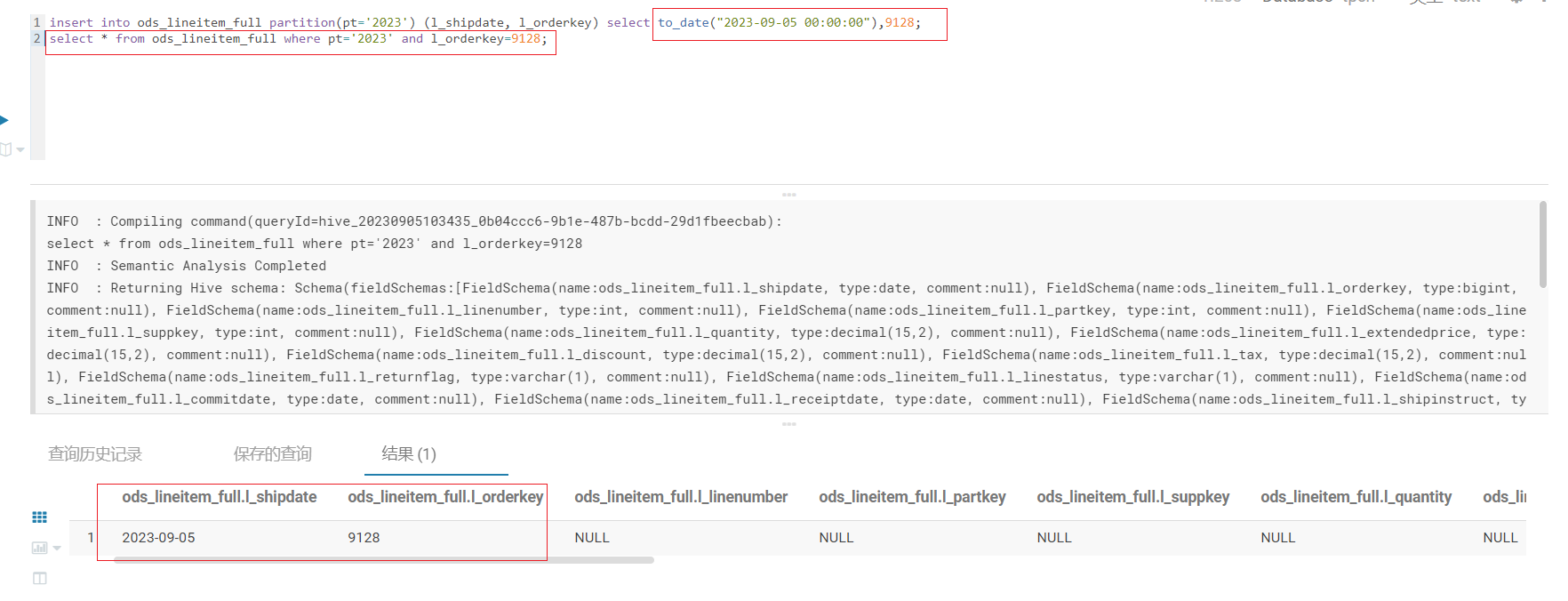
hive指定字段插入数据,包含了分区表和非分区表
1、建表 语句如下: CREATE EXTERNAL TABLE ods_lineitem_full (l_shipdate date,l_orderkey bigint,l_linenumber int,l_partkey int,l_suppkey int,l_quantity decimal(15, 2),l_extendedprice decimal(15, 2),l_discount de…...
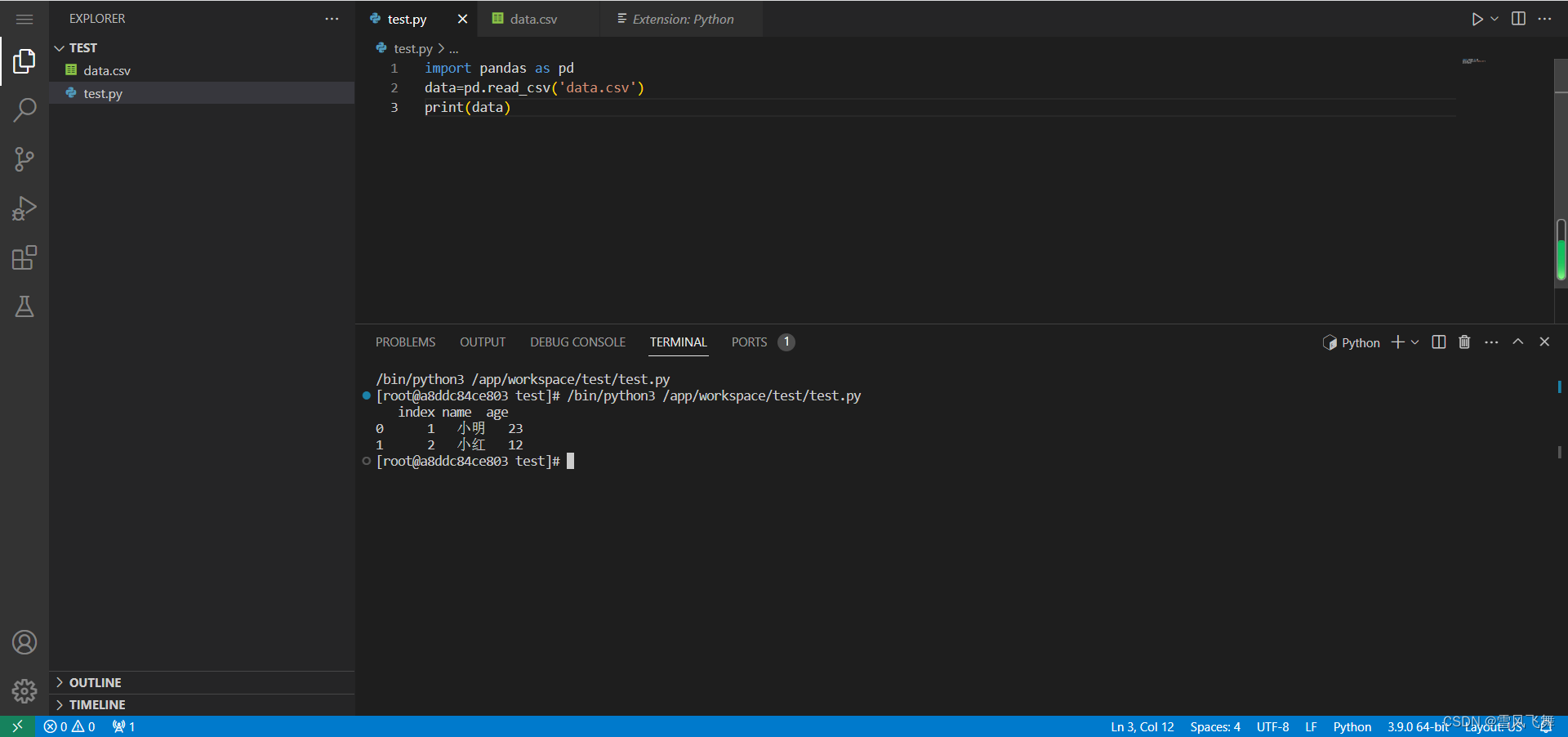
浏览器端vscode docker搭建(附带python环境)
dockerfile from centos:7 #安装python环境 run yum -y install wget openssl-devel bzip2-devel expat-devel gdbm-devel readline-devel zlib-devel libffi-devel gcc make run wget https://www.python.org/ftp/python/3.9.0/Python-3.9.0.tgz run tar -xvf Python-3.9.…...
Echarts图表跟随父容器的变化自适应
如果页面中有多个图表 隐藏/展开左边侧边栏echarts图表自适应 <div class"line"><div class"title">制冷站关键参数</div><div id"chartLine1" style"width: 100%;height:85%;"></div></div><…...
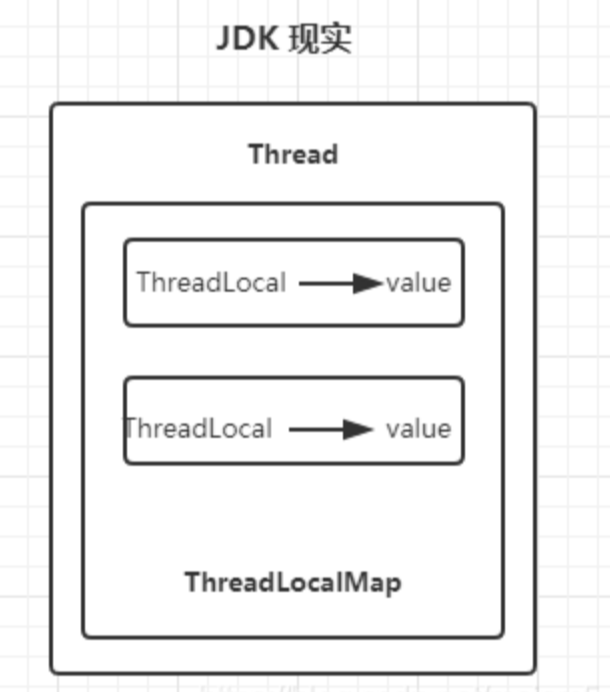
【多线程】ThreadLocal是什么?有哪些使用场景?使用ThreadLocal需要注意些什么?
文章目录 前言一、ThreadLocal 是什么?二、有哪些使用场景?三、实现原理四、在线程池中使用 ThreadLocal 为什么可能导致内存泄露呢?五、线程池中,如何正确使用 ThreadLocal?六、ThreadLocal 核心方法 前言 一、Threa…...
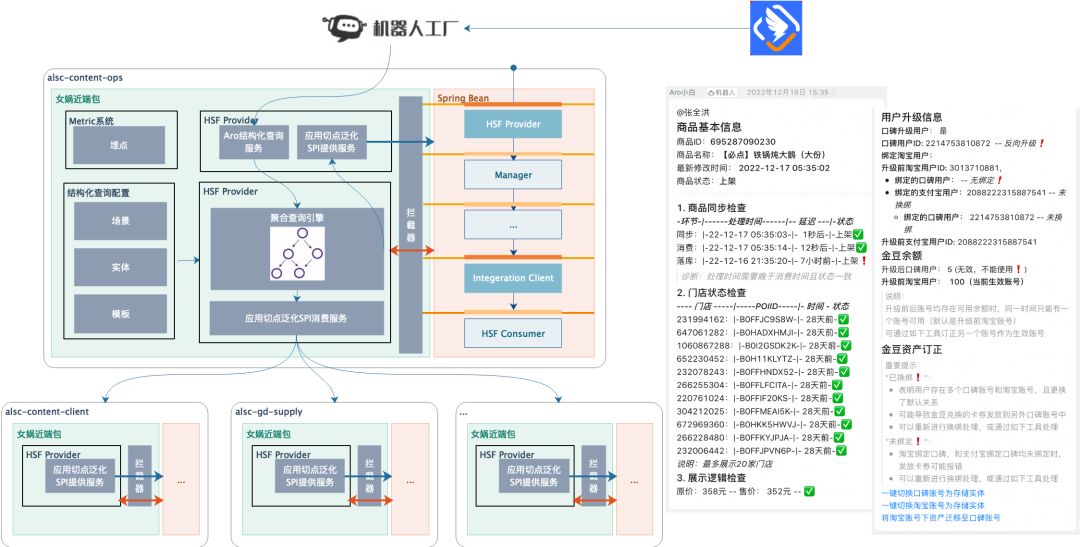
一种基于动态代理的通用研发提效解决方案
作为一名研发人员,除了业务开发之外,研发提效是一个永恒的话题,而女娲正是这一话题下进行的一次全面的剖析和实践。 作者:张全洪(钝悟) 一、女娲是什么 女娲是业务研发同学(开发、测试、运维)在软件迭代的…...
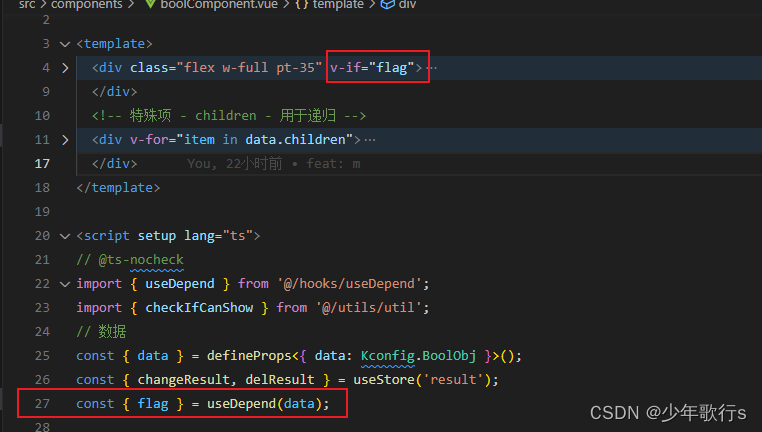
【vue3】一些关于hooks的使用经验
前言 最近接到了一个需求,隔壁嵌入式部门希望我们用前端解析渲染Kconfig表单。这篇文章用来记录一下本次使用hook pinia vue3的经验 hooks hooks的概念最早是在 React 中听到的,虽然早些时间也写过一点react,但也只是照葫芦画瓢…...

面试系列 - Java 并发容器详解
Java 并发容器是一组用于在多线程环境下安全访问和操作数据的数据结构。它们提供了线程安全的集合和映射,使开发者能够更轻松地处理并发编程问题。 一、Java并发容器 ConcurrentHashMap: 它是一个高效的并发哈希表,支持多线程并发操作而不需…...
使用动态住宅代理还能带来哪些好处?
一、什么是动态住宅代理ip 动态住宅代理是一种代理技术,它利用代理服务器中转用户和目标服务器之间的网络流量,实现用户真实位置的屏蔽。代理提供商会有自己的ip大池子,当你通过代理服务器向网站发送请求时,服务器会从池子中选中…...
)
笙默考试管理系统-MyExamTest----codemirror(18)
笙默考试管理系统-MyExamTest----codemirror(18) 目录 一、 笙默考试管理系统-MyExamTest----codemirror 二、 笙默考试管理系统-MyExamTest----codemirror 三、 笙默考试管理系统-MyExamTest----codemirror 四、 笙默考试管理系统-MyExamTest---…...

TGA格式文件转材质
今天淘宝上买了一个美女的模型,是blender的源文件,上面说有fbx格式的。我用unity,所以觉得应该可以用。文件内容如下图: FBX文件夹打开后,内容如下图所示,当时就预感到可能没有色彩。 unity打开后果然发现只…...

IP应用场景查询API:深入了解网络用户行为的利器
前言 随着数字时代的不断发展,互联网已经成为人们生活的重要组成部分。而随着越来越多的业务和社交活动迁移到在线平台上,了解和理解网络用户行为变得至关重要。为了满足这个需求,IP 应用场景查询 API 崭露头角,成为深入了解网络…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
