MATLAB中movmean函数用法
目录
语法
说明
示例
向量的中心移动平均值
向量的尾部移动平均值
矩阵的移动平均值
包含缺失值的向量的移动平均值
基于样本点计算移动平均值
仅返回满窗口平均值
movmean函数的功能是对数据进行移动求平均值。
语法
M = movmean(A,k)
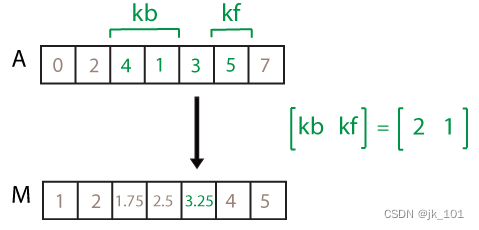
M = movmean(A,[kb kf])
M = movmean(___,dim)
M = movmean(___,nanflag)
M = movmean(___,Name,Value)说明
M = movmean(A,k) 返回由局部 k 个数据点的均值组成的数组,其中每个均值是基于 A 的相邻元素的长度为 k 的滑动窗计算得出。当 k 为奇数时,窗以当前位置的元素为中心。当 k 为偶数时,窗以当前元素及其前一个元素为中心。当没有足够的元素填满窗时,窗将自动在端点处截断。当窗口被截断时,只根据窗口内的元素计算平均值。M 与 A 的大小相同。
-
如果 A 是向量,movmean 将沿向量 A 的长度运算。
-
如果 A 是多维数组,则 movmean 沿 A 的大小不等于 1 的第一个维度进行运算。
M = movmean(A,[kb kf]) 通过长度为 kb+kf+1 的窗口计算均值,其中包括当前位置的元素、前面的 kb 个元素和后面的 kf 个元素。
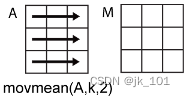
M = movmean(___,dim) 为上述任一语法指定 A 的运算维度。例如,如果 A 是矩阵,则 movmean(A,k,2) 沿 A 的列运算,计算每行的 k 元素移动均值。
M = movmean(___,nanflag) 指定包含还是省略 A 中的 NaN 值。例如,movmean(A,k,"omitnan") 在计算每个均值时会忽略 NaN 值。默认情况下,movmean 包括 NaN 值。
M = movmean(___,Name,Value) 使用一个或多个名称-值参数指定移动平均值的其他参数。例如,如果 x 是时间值向量,则 movmean(A,k,"SamplePoints",x) 相对于 x 中的时间计算移动平均值。
示例
向量的中心移动平均值
计算行向量的三点中心移动平均值。当端点处的窗口中少于三个元素时,将根据可用元素计算平均值。
A = [4 8 6 -1 -2 -3 -1 3 4 5];
M = movmean(A,3)
M = 1×106.0000 6.0000 4.3333 1.0000 -2.0000 -2.0000 -0.3333 2.0000 4.0000 4.5000向量的尾部移动平均值
计算行向量的三点尾部移动平均值。当端点处的窗口中少于三个元素时,将根据可用元素计算平均值。
A = [4 8 6 -1 -2 -3 -1 3 4 5];
M = movmean(A,[2 0])
M = 1×104.0000 6.0000 6.0000 4.3333 1.0000 -2.0000 -2.0000 -0.3333 2.0000 4.0000矩阵的移动平均值
计算矩阵中每行的三点中心移动平均值。窗从第一行开始,沿水平方向移动到该行的末尾,然后移到第二行,依此类推。维度参数为 2,即跨 A 的列移动窗。
A = [4 8 6; -1 -2 -3; -1 3 4]
A = 3×34 8 6-1 -2 -3-1 3 4M = movmean(A,3,2)
M = 3×36.0000 6.0000 7.0000-1.5000 -2.0000 -2.50001.0000 2.0000 3.5000
包含缺失值的向量的移动平均值
计算包含两个 NaN 元素的行向量的三点中心移动平均值。
A = [4 8 NaN -1 -2 -3 NaN 3 4 5];
M = movmean(A,3)
M = 1×106.0000 NaN NaN NaN -2.0000 NaN NaN NaN 4.0000 4.5000
重新计算平均值,但忽略 NaN 值。当 movmean 忽略 NaN 元素时,它将根据窗中的剩余元素计算平均值。
M = movmean(A,3,"omitnan")
M = 1×106.0000 6.0000 3.5000 -1.5000 -2.0000 -2.5000 0 3.5000 4.0000 4.5000
基于样本点计算移动平均值
根据时间向量 t,计算 A 中数据的 3 小时中心移动平均值。
A = [4 8 6 -1 -2 -3];
k = hours(3);
t = datetime(2016,1,1,0,0,0) + hours(0:5)
t = 1x6 datetime01-Jan-2016 00:00:00 01-Jan-2016 01:00:00 01-Jan-2016 02:00:00 01-Jan-2016 03:00:00 01-Jan-2016 04:00:00 01-Jan-2016 05:00:00M = movmean(A,k,"SamplePoints",t)
M = 1×66.0000 6.0000 4.3333 1.0000 -2.0000 -2.5000仅返回满窗口平均值
计算行向量的三点中心移动平均值,但在输出中舍弃使用的点数少于三个的计算。也就是说,只返回从满的三元素窗口计算的平均值,而舍弃端点计算。
A = [4 8 6 -1 -2 -3 -1 3 4 5];
M = movmean(A,3,"Endpoints","discard")
M = 1×86.0000 4.3333 1.0000 -2.0000 -2.0000 -0.3333 2.0000 4.0000参数说明
A:输入数组,指定为向量、矩阵或多维数组。
k:窗长度,指定为数值或持续时间标量。当 k 是正整数标量时,中心平均值包括当前位置的元素以及周围的相邻元素。
例如,movmean(A,3) 计算一个由局部三点均值组成的数组。

[kb kf]:定向窗长度,指定为包含两个元素的数值或持续时间行向量。当 kb 和 kf 为正整数标量时,将基于 kb+kf+1 个元素进行计算。该计算包括当前位置的元素、当前位置前面的 kb 个元素以及当前位置后面的 kf 个元素。
例如,movmean(A,[2 1]) 计算一个由局部四点均值组成的数组。
dim:沿其运算的维度,指定为正整数标量。如果不指定维度,则默认为第一个大于 1 的数组维度。
维度 dim 表示 movmean 运算所沿的维度,即指定窗的移动方向。
以一个 m×n 输入矩阵 A 为例:
·movmean(A,k,1) 为 A 的每列计算包含 k 个元素的移动均值,并返回一个 m×n 矩阵。

·movmean(A,k,2) 为 A 的每行计算包含 k 个元素的移动均值,并返回一个 m×n 矩阵。
nanflag:缺失值条件,指定为下列值之一:
-
"includemissing" 或 "includenan" - 在计算每个均值时包括 A 中的 NaN 值。如果窗中的任一元素是 NaN,则 M 中的对应元素是 NaN。"includemissing" 和 "includenan" 具有相同的行为。
-
"omitmissing" 或 "omitnan" - 忽略 A 中的 NaN 值,并基于较少的点计算每个均值。如果窗中的所有元素都是 NaN,则 M 中的对应元素是 NaN。"omitmissing" 和 "omitnan" 具有相同的行为。
相关文章:

MATLAB中movmean函数用法
目录 语法 说明 示例 向量的中心移动平均值 向量的尾部移动平均值 矩阵的移动平均值 包含缺失值的向量的移动平均值 基于样本点计算移动平均值 仅返回满窗口平均值 movmean函数的功能是对数据进行移动求平均值。 语法 M movmean(A,k) M movmean(A,[kb kf]) M mov…...
IIS短文件名泄露漏洞复现
IIS短文件名泄露漏洞复现 前言一、漏洞描述二、漏洞原理1.什么是短文件2.短文件特征 三、漏洞验证三、漏洞防御总结 前言 IIS短文件名泄露漏洞比较老了,而且只适合于windowsiisasp的网络结构,所有如下的复现步骤看下就行了,关键是要弄懂原理…...

万字解读 Android 车机核心 :CarService 的构成和链路~
前言 关于 Android 车机,之前分析过方控上自定义按键的输入机制和中控上旋钮输入的原理,但都局限于 Car Service 内 Input 相关模块。 一文了解 Android 车机如何处理中控的旋钮输入从实体按键看 Android 车载的自定义事件机制 本文将结合 Android 系…...

C#使用Panel
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System...
)
Jabbi的Rust学习日记(一)
Rust环境安装 Windows:Install Rust - Rust Programming Language (rust-lang.org) 访问网页,下载64bit | 32bit 版本 下载完成后打开,直接enter即可 Linux:输入指令 curl https://sh.rustup.rs-sSf | sh 我会报错,好像是链接不到这个网址&a…...
电脑磁盘分区形式是什么?如何更改?
磁盘分区形式介绍 在了解为什么以及如何更改分区形式之前,让我们对磁盘分区形式有一个基本的了解。一般来说,分区形式是指主引导记录(MBR)和 GUID 分区表(GPT)。 MBR和GPT是Windows系统中常用…...

Outlook无需API开发连接钉钉群机器人,实现新增会议日程自动发送群消息通知
Outlook用户使用场景: 在企业中,会议和活动的顺利举行对于业务运转和团队协作至关重要。然而,计划的变动总是无法避免,这可能会导致其他人的计划受到影响,打乱原有的安排。为了解决这个问题,许多企业开始使…...
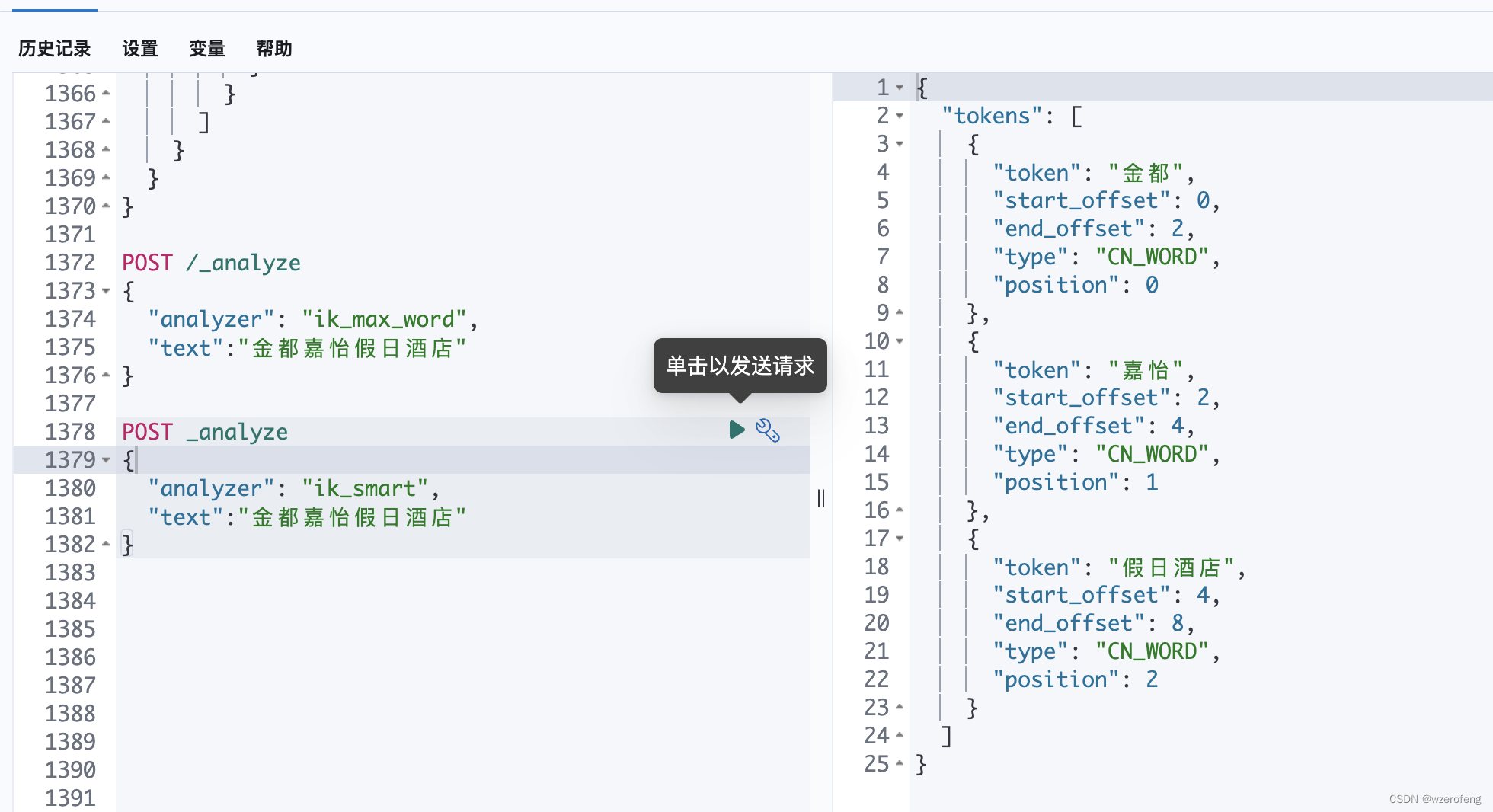
elasticsearch分析插件 安装analysis-ik
首先下载安装es 和 插件 ,注意 两者的版本要保持一致,如果要用到kibana 则三者保持一致 ik:https://github.com/medcl/elasticsearch-analysis-ik/releases es/kibana:https://www.elastic.co/cn/downloads/past-releases/ 然后在 es— elast…...
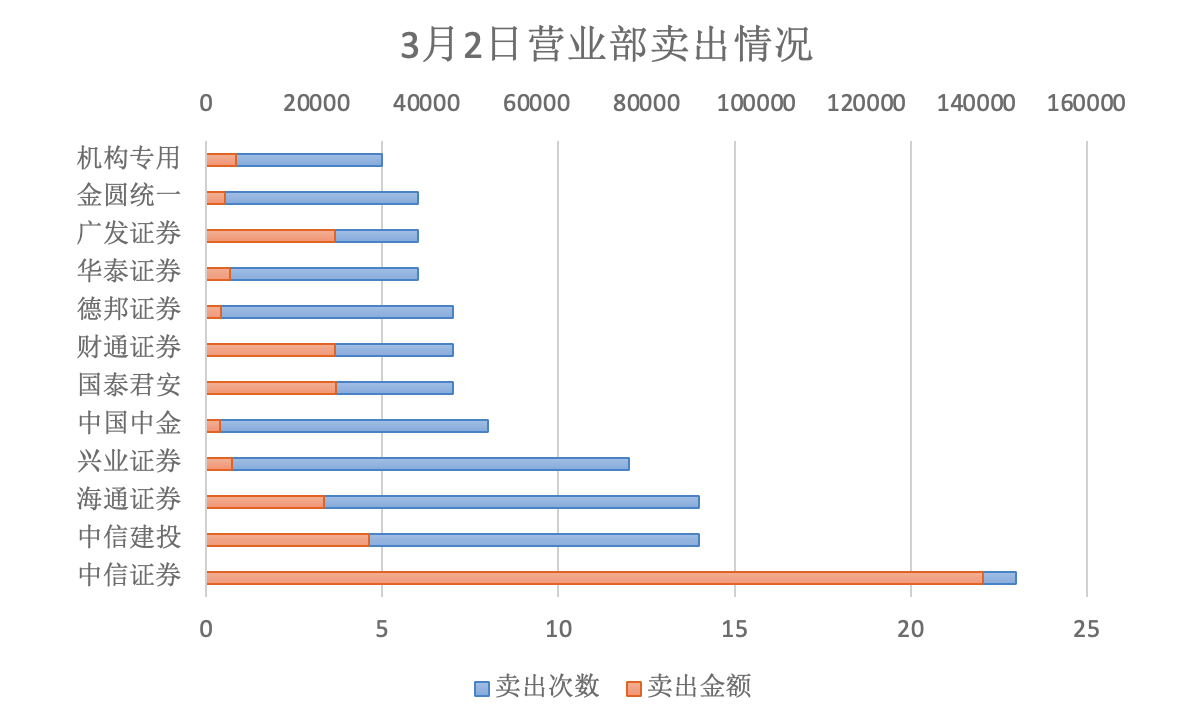
2023年股票大宗减持研究报告
第一章 股票大宗减持概述 1.1 概念 大宗减持是指通过大宗交易的方式进行减持,即达到规定的最低限额的证券单笔买卖申报,买卖双方经过协议达成一致并经交易所确定成交的证券交易,其中A股单笔交易数量在30万股(含)以上…...
VS编译.cu文件源文件无法打开matrix.h和mex.h问题
配置好cu和VS相关库文件后CUDA程序仍然报错:无法打开matrix.h和mex.h,解决办法: (1)这两个头文件是matlab中的,可能无法直接在VS中调用,可以通过添加外部依赖项的方法将matlab中的头文件的文件路…...
)
小bugs搜集和解决方法,亲测有效(2022-2023)
有些小bugs几行指令就能解决,写太多不好,这里就进行一个2022-2023这段时间的bugs collection和solution。 Deep Learning How to make really empty tensor? a nn.Torch([]) b torch.empty(2,3) for i in rang(3):a torch.cat(a, b, dim0)Mismatc…...
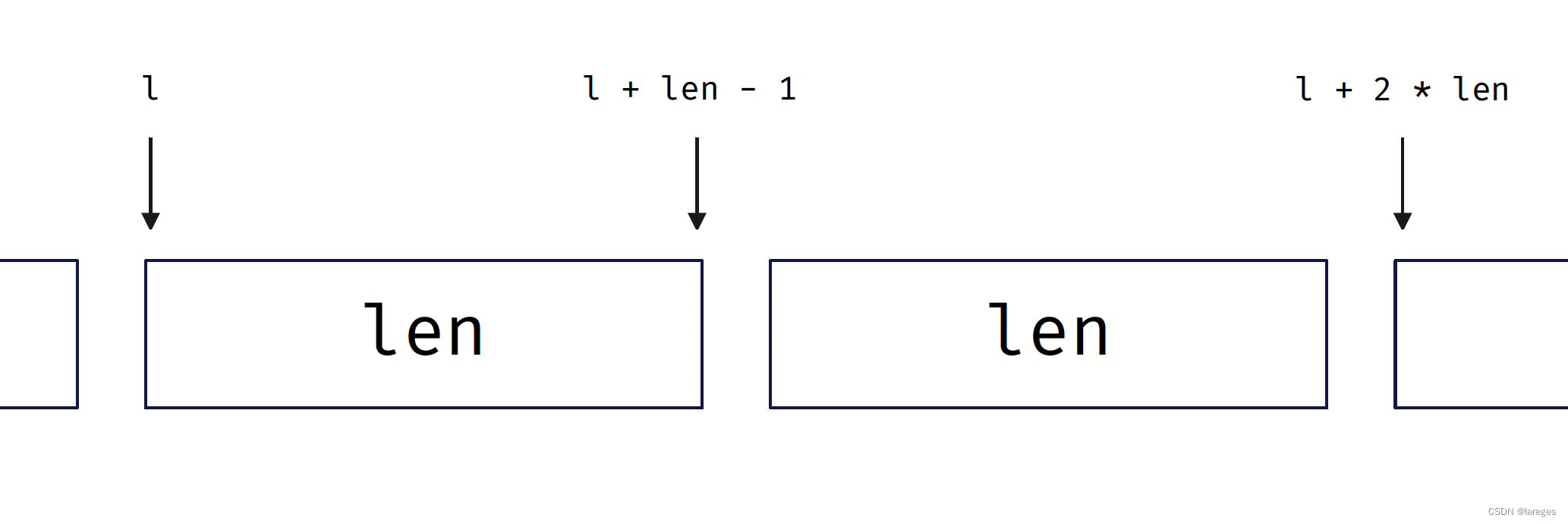
归并排序和快速排序的两种实现
在此之前我们已经介绍过归并排序和快速排序:浅谈归并排序与快速排序,但其中的实现都是基于递归的。本文将重新温故这两种算法并给出基于迭代的实现。 目录 1. 归并排序1.1 基于递归1.2 基于迭代 2. 快速排序2.1 基于递归2.2 基于迭代 1. 归并排序 1.1 基…...

C#,《小白学程序》第十四课:随机数(Random)第一,几种随机数的计算方法与代码
1 文本格式 /// <summary> /// 《小白学程序》第十四课:随机数(Random)第一,几种随机数的计算方法与代码 /// 本课初步接触一下随机数。 /// </summary> /// <param name"sender"></param> ///…...

[杂谈]-快速了解Modbus协议
快速了解Modbus协议 文章目录 快速了解Modbus协议1、为何 Modbus 如此受欢迎2、范围和数据速率3、逻辑电平4、层数5、网络与通讯6、数据帧格式7、数据类型8、服务器如何存储数据9、总结 Modbus 是一种流行的低速串行通信协议,广泛应用于自动化行业。 该协议由 Mo…...
WhatsApp的两个商业模式该如何选择
WhatsApp Business 是什么 目前 WhatsApp 提供两种商业模式,企业应根据自身需求选择相应版本。 第一个版本是 WhatsApp Business:初创企业只需一个手机应用程序,便可以个体单位与客户轻松互动; 另一个版本是 WhatsApp Business APIÿ…...
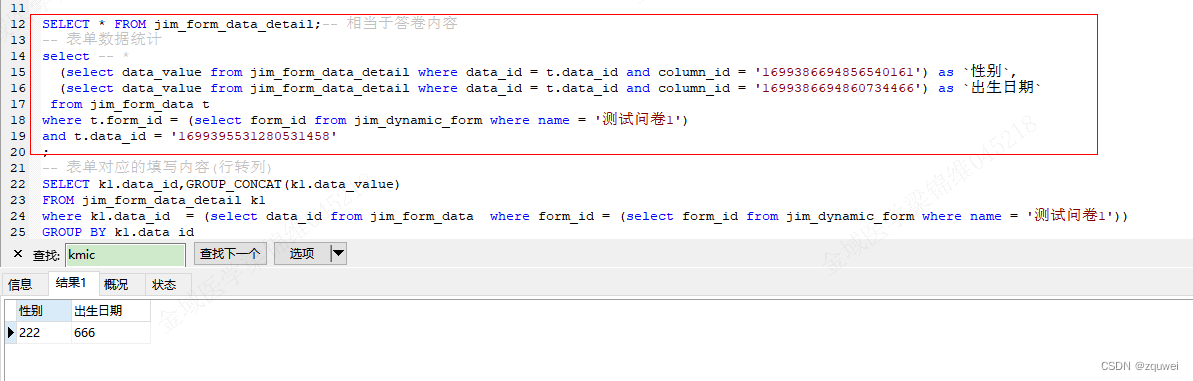
动态表单设计
动态表单设计 背景方案讨论基于上面分析,对比调研,自定义动态表单数据模型表单详解(一) 表单模板:jim_dynamic_form(二)表单数据类型:jim_form_data_type(三)…...

JAR will be empty - no content was marked for inclusion!
现象 在对自建pom依赖组件打包时,出现JAR will be empty - no content was marked for inclusion!错误。 方案 在pom中怎么加packaging标签内容为pom,标识只打包pom文件 <?xml version"1.0" encoding"UTF-8"?> ...<grou…...
软件生命周期及流程【软件测试】
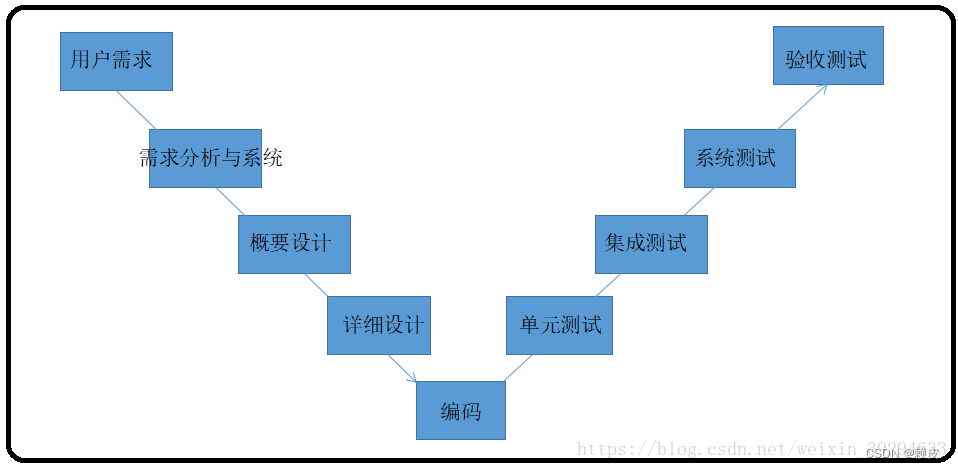
软件的生命周期 软件生命周期是软件开始研制到最终被废弃不用所经历的各个阶段。 瀑布型生命周期模型 规定了它们自上而下、相互衔接的固定次序,如同瀑布流水,逐级下落,具有顺序性和依赖性。每个阶段规定文档并需进行评审。 特点ÿ…...
2023高教社杯数学建模E题思路代码 - 黄河水沙监测数据分析
# 1 赛题 E 题 黄河水沙监测数据分析 黄河是中华民族的母亲河。研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变 化和人民生活的影响, 以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾 等方面都具有重要的理论指导意义。 附件 1 给出了位…...
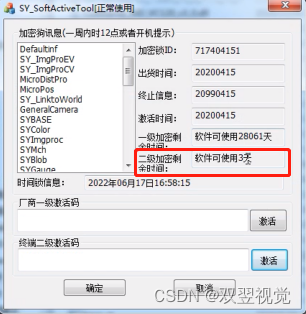
双翌保养码使用指南方法(一)
保养码使用指南一 为了确保软件的正常运行和有效使用,正确地使用保养码是至关重要的。以下是保养码使用的简单指南,以帮助您进行正确的操作。 1. 打开软件入口:首先,在您的电脑上打开文件夹,并找到s-y softactive tool…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...
