算法刷题记录-DP(LeetCode)
746. Min Cost Climbing Stairs
代码
int minCostClimbingStairs(vector<int>& cost) {if (cost.size()<2){return 0;}int cache[cost.size()+1];cache[0]=0;cache[1]=0;for (int i = 2; i <= cost.size(); ++i) {cache[i]= min(cache[i-2]+cost[i-2],cache[i-1]+cost[i-1]);}return cache[cost.size()];}
*873. Length of Longest Fibonacci Subsequence
思路
定义 f [ i ] [ j ] f[i][j] f[i][j]为使用 a r r [ i ] arr[i] arr[i] 为斐波那契数列的最后一位,使用 a r r [ j ] arr[j] arr[j] 为倒数第二位(即 a r r [ i ] arr[i] arr[i] 的前一位)时的最长数列长度。
不失一般性考虑 f [ i ] [ j ] f[i][j] f[i][j]该如何计算,首先根据斐波那契数列的定义,我们可以直接算得 a r r [ j ] arr[j] arr[j] 前一位的值为 a r r [ i ] − a r r [ j ] arr[i]−arr[j] arr[i]−arr[j],而快速得知 a r r [ i ] − a r r [ j ] arr[i]−arr[j] arr[i]−arr[j]值的坐标 t t t,可以利用 arr 的严格单调递增性质,使用「哈希表」对坐标进行转存,若坐标 t t t存在,并且符合 t < j t<j t<j,说明此时至少凑成了长度为 333 的斐波那契数列,同时结合状态定义,可以使用 f [ j ] [ t ] f[j][t] f[j][t]来更新 f [ i ] [ j ] f[i][j] f[i][j],即有状态转移方程:
f [ i ] [ j ] = m a x ( 3 , f [ j ] [ t ] + 1 ) f [ i ] [ j ] = max ( 3 , f [ j ] [ t ] + 1 ) f[i][j]=max(3,f[j][t]+1)f[i][j] = \max(3, f[j][t] + 1) f[i][j]=max(3,f[j][t]+1)f[i][j]=max(3,f[j][t]+1)
同时,当我们「从小到大」枚举 iii,并且「从大到小」枚举 j j j 时,我们可以进行如下的剪枝操作:
- 可行性剪枝:当出现 a r r [ i ] − a r r [ j ] > = a r r [ j ] arr[i]−arr[j]>=arr[j] arr[i]−arr[j]>=arr[j],说明即使存在值为 a r r [ i ] − a r r [ j ] arr[i]−arr[j] arr[i]−arr[j]的下标 t t t,根据 arr 单调递增性质,也不满足 t < j < i t<j<i t<j<i 的要求,且继续枚举更小的 j j j ,仍然有 a r r [ i ] − a r r [ j ] > = a r r [ j ] arr[i]−arr[j]>=arr[j] arr[i]−arr[j]>=arr[j],仍不合法,直接 break 掉当前枚举 j j j的搜索分支;
- 最优性剪枝:假设当前最大长度为 ans,只有当 j + 2 > a n s j+2>ans j+2>ans,我们才有必要往下搜索, j + 2 j+2 j+2 的含义为以 a r r [ j ] arr[j] arr[j] 为斐波那契数列倒数第二个数时的理论最大长度。
代码
public int lenLongestFibSubseq(int[] arr) {int ans=0;HashMap<Integer,Integer> finder=new HashMap<>();for (int i = 0; i < arr.length; i++) {finder.put(arr[i],i);}int[][] cache=new int[arr.length][arr.length];for (int i = 2; i < arr.length; i++) {for (int j = i-1; j >= 1; j--) {int residual=arr[i]-arr[j];if (residual>=arr[j]){break;}if (finder.containsKey(arr[i]-arr[j])){cache[i][j]=Math.max(3,cache[j][finder.get(residual)]+1);ans=Math.max(ans,cache[i][j]);}}}return ans;}
*877. Stone Game
数学解法
事实上,这还是一道很经典的博弈论问题,也是最简单的一类博弈论问题。
为了方便,我们称「石子序列」为石子在原排序中的编号,下标从 1开始。
由于石子的堆数为偶数,且只能从两端取石子。因此先手后手所能选择的石子序列,完全取决于先手每一次决定。
证明如下:
由于石子的堆数为偶数,对于先手而言:每一次的决策局面,都能「自由地」选择奇数还是偶数的序列,从而限制后手下一次「只能」奇数还是偶数石子。
具体的,对于本题,由于石子堆数为偶数,因此先手的最开始局面必然是[奇数, 偶数],即必然是「奇偶性不同的局面」;当先手决策完之后,交到给后手的要么是[奇数,奇数] 或者 [偶数,偶数],即必然是「奇偶性相同的局面」;后手决策完后,又恢复「奇偶性不同的局面」交回到先手 …
不难归纳推理,这个边界是可以应用到每一个回合。
因此先手只需要在进行第一次操作前计算原序列中「奇数总和」和「偶数总和」哪个大,然后每一次决策都「限制」对方只能选择「最优奇偶性序列」的对立面即可。
同时又由于所有石子总和为奇数,堆数为偶数,即没有平局,所以先手必胜。
bool stoneGame(vector<int>& piles) {return true;}
动态规划
定义 f[l][r] 为考虑区间 [l,r],在双方都做最好选择的情况下,先手与后手的最大得分差值为多少。
那么 f[1][n] 为考虑所有石子,先手与后手的得分差值:
- f [ 1 ] [ n ] > 0 f[1][n]>0 f[1][n]>0,则先手必胜,返回 True
- f [ 1 ] [ n ] < 0 f[1][n]<0 f[1][n]<0,则先手必败,返回 False
不失一般性的考虑 f [ l ] [ r ] f[l][r] f[l][r]如何转移。根据题意,只能从两端取石子(令 piles 下标从 1 开始),共两种情况:
- 从左端取石子,价值为
piles[l - 1];取完石子后,原来的后手变为先手,从[l+1,r]区间做最优决策,所得价值为f[l+1][r]。因此本次先手从左端点取石子的话,双方差值为:
p i l e s [ l − 1 ] − f [ l + 1 ] [ r ] piles[l−1]−f[l+1][r] piles[l−1]−f[l+1][r] - 从右端取石子,价值为
piles[r−1];取完石子后,原来的后手变为先手,从[l,r−1]区间做最优决策,所得价值为f[l][r−1]。因此本次先手从右端点取石子的话,双方差值为:
p i l e s [ r − 1 ] − f [ l ] [ r − 1 ] piles[r−1]−f[l][r−1] piles[r−1]−f[l][r−1]
双方都想赢,都会做最优决策(即使自己与对方分差最大)。因此 f [ l ] [ r ] f[l][r] f[l][r] 为上述两种情况中的最大值。
根据动态规划的状态转移方程,计算 dp [ i ] [ j ] \textit{dp}[i][j] dp[i][j] 需要使用 dp[i+1][j]和 dp[i][j−1]的值,即区间 [i+1,j] 和 [i,j−1]的状态值需要在区间[i,j] 的状态值之前计算,因此计算 dp[i][j] 的顺序可以是以下两种。
从小到大遍历每个区间长度,对于每个区间长度依次计算每个区间的状态值。
从大到小遍历每个区间开始下标 i i i,对于每个区间开始下标 i i i 从小到大遍历每个区间结束下标 jjj,依次计算每个区间 [i, j] 的状态值。
计算得到 dp[0][n−1]即为 Alice 与 Bob 的石子数量之差最大值。如果 d p [ 0 ] [ n − 1 ] > 0 dp[0][n−1]>0 dp[0][n−1]>0,则 Alice 赢得游戏,返回true,否则 Bob 赢得游戏,返回 false。
class Solution {public boolean stoneGame(int[] ps) {int n = ps.length;int[][] f = new int[n + 2][n + 2]; for (int len = 1; len <= n; len++) { // 枚举区间长度for (int l = 1; l + len - 1 <= n; l++) { // 枚举左端点int r = l + len - 1; // 计算右端点int a = ps[l - 1] - f[l + 1][r];int b = ps[r - 1] - f[l][r - 1];f[l][r] = Math.max(a, b);}}return f[1][n] > 0;}
}
*915. Partition Array into Disjoint Intervals
思路
根据题意,我们知道本质是求分割点,使得分割点的「左边的子数组的最大值」小于等于「右边的子数组的最小值」。
我们可以先通过一次遍历(从后往前)统计出所有后缀的最小值 min,其中 min[i] = x 含义为下标范围在
[ i , n − 1 ] [i,n−1] [i,n−1] 的 n u m s [ i ] nums[i] nums[i]的最小值为 x,然后再通过第二次遍历(从前往后)统计每个前缀的最大值(使用单变量进行维护),找到第一个符合条件的分割点即是答案。
代码
public int partitionDisjoint(int[] nums) {int[] min=new int[nums.length];int[] max=new int[nums.length];min[nums.length-1]=nums[nums.length-1];for (int i = nums.length-2; i >=0 ; i--) {min[i]=Math.min(min[i+1],nums[i]);}max[0]=nums[0];for (int i = 1; i < nums.length; i++) {max[i]=Math.max(nums[i],max[i-1]);}int ans=0;for (int i = nums.length-2; i >=0; i--) {if (max[i]<=min[i+1]){ans=i;}}return ans+1;}
926. Flip String to Monotone Increasing
思路
根据题意可知,字符有0和1两种状态,所以我们维护一个二维的cache数组来记录每个字符的状况。
cache[i][0]表示第i个字符是0的变换次数,cache[i][1]表示第i个字符是1的变换次数。
根据单调性: 若 s [ i − 1 ] = = 0 s[i-1] == 0 s[i−1]==0,s[i]是0或者1都可以保持单调性。
若 s [ i − 1 ] = = 1 s[i-1] == 1 s[i−1]==1,s[i]则必须为1才可以保持单调性(必须满足i-1是1)。
所以
cache[i][0] = cache[i-1][0] + (s[i] == '1' ? 1 : 0);//(自己是0,则前边都是0)
cache[i][1] = Math.min(cache[i-1][0],cache[i-1][1]) + (s[i] == '0' ? 1 : 0);//(自己是1,前边0或者1都可以)
最后result = Math.min(cache[i][0],cache[i][1])
代码
public int minFlipsMonoIncr(String s) {int cache[][]=new int[s.length()][2];char[] arr=s.toCharArray();cache[0][0]=arr[0]=='0'?0:1;cache[0][1]=1-cache[0][0];for (int i = 1; i < arr.length; i++) {cache[i][0]=cache[i-1][0]+(arr[i]=='0'?0:1);cache[i][1]=Math.min(cache[i-1][0],cache[i-1][1])+(arr[i]=='1'?0:1);}return Math.min(cache[s.length()-1][0],cache[s.length()-1][1]);}
相关文章:
)
算法刷题记录-DP(LeetCode)
746. Min Cost Climbing Stairs 代码 int minCostClimbingStairs(vector<int>& cost) {if (cost.size()<2){return 0;}int cache[cost.size()1];cache[0]0;cache[1]0;for (int i 2; i < cost.size(); i) {cache[i] min(cache[i-2]cost[i-2],cache[i-1]cost[i…...

Springboot整合Neo4J图数据库
1.引入依赖 JDK11, neo4J4.4.23 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.15</version><relativePath/> <!-- lookup parent …...

Unity 2018发布在iOS 16.3偶尔出现画面不动的问题
1)Unity 2018发布在iOS 16.3偶尔出现画面不动的问题 2)IL2CPP在Xcode下增量编译问题 3)帧同步实现PuppetMaster布娃娃系统的问题 这是第351篇UWA技术知识分享的推送,精选了UWA社区的热门话题,涵盖了UWA问答、社区帖子等…...
蠕虫病毒流量分析案例
背景 某供排水集团的网络管理员对其网络的健康状况持认可态度,表示网络运行正常,没有发现异常行为。然而,由于网络环境变得越来越复杂,仅凭借传统的网络经验已经不能全面了解网络情况。因此,我们为供排水集团安装了Ne…...
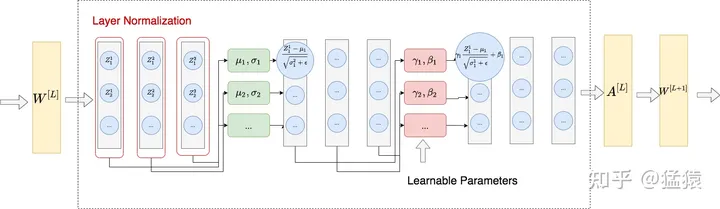
Transformer(一)—— Attention Batch Normalization
Transformer详解 一、RNN循环神经网络二、seq2seq模型三、Attention(注意力机制)四、Transformer4.1 self attention4.2 self-attention的变形——Multi-head Self-attention4.3 Masked Attention4.4 Positional Encoding4.5 Batch Normalization4.6 Lay…...
2023高教社杯数学建模C题思路代码 - 蔬菜类商品的自动定价与补货决策
# 1 赛题 在生鲜商超中,一般蔬菜类商品的保鲜期都比较短,且品相随销售时间的增加而变差, 大部分品种如当日未售出,隔日就无法再售。因此, 商超通常会根据各商品的历史销售和需 求情况每天进行补货。 由于商超销售的蔬菜…...

【C++漂流记】一文搞懂类与对象的封装
本篇文章主要说明了类与对象中封装的有关知识,包括属性和行为作为整体、访问权限、class与struct的区别、成员属性的私有化,希望这篇文章可以帮助你更好的了解类与对象这方面的知识。 文章目录 一、属性和行为作为整体二、访问权限三、class与struct的区…...
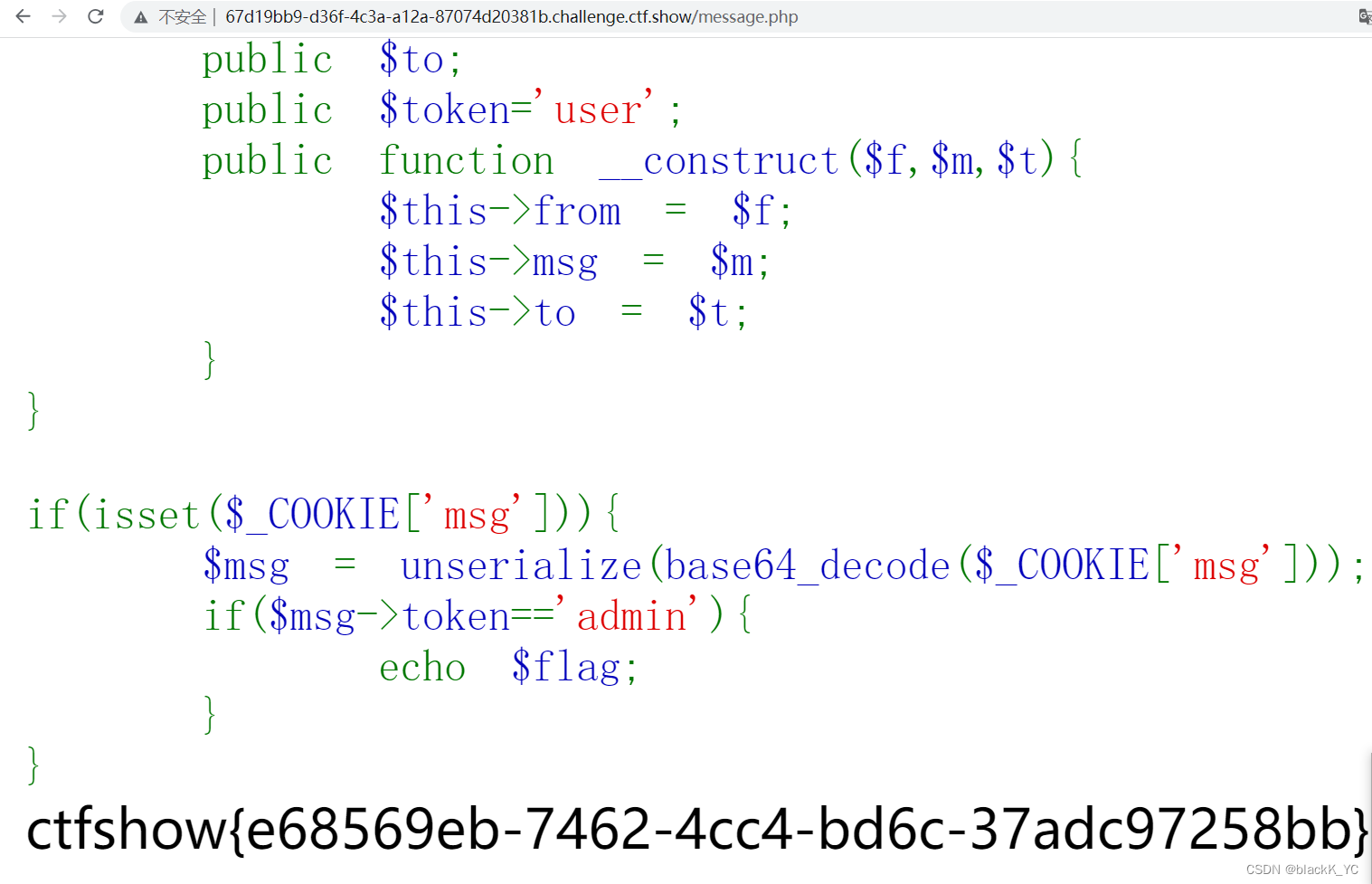
ctfshow 反序列化
PHP反序列化前置知识 序列化和反序列化 对象是不能在字节流中传输的,序列化就是把对象转化为字符串以便存储和传输,反序列化就是将字符串转化为对象 魔术方法 __construct() //构造,当对象new时调用 __wakeup() //执行unserialize()时&am…...

数据结构:线性表之-单向链表(无头)
目录 什么是单向链表 顺序表和链表的区别和联系 顺序表: 链表: 链表表示(单项)和实现 1.1 链表的概念及结构 1.2单链表(无头)的实现 所用文件 将有以下功能: 链表定义 创建新链表元素 尾插 头插 尾删 头删 查找-给一个节点的…...

为IT服务台构建自定义Zia操作
Zia是manageengine的商业人工智能助手,是ServiceDesk Plus Cloud的虚拟会话支持代理。使用Zia,您可以优化帮助台管理,还可以缩小最终用户与其帮助台之间的差距,Zia通过执行预配置的操作来帮助用户完成他们的服务台任务。 例如&…...
【C/C++】BMP格式32位转24位
问题 如题 解决方法 bmp文件格式参考:【C/C++】BITMAP格式分析_vc++ bitmap头文件_sunriver2000的博客-CSDN博客BITMAP文件大体上分成四个部分,如下表所示。文件部分长度(字节)位图文件头 Bitmap File Header14位图信息数据头 Bitmap Info Header40调色板 Palette4*n (n≥…...

合宙Air724UG LuatOS-Air LVGL API控件-滑动条 (Slider)
滑动条 (Slider) 滑动条看起来和进度条是有些是有些像,但不同的是滑动条可以进行数值选择。 示例代码 -- 回调函数 slider_event_cb function(obj, event)if event lvgl.EVENT_VALUE_CHANGED then local val (lvgl.slider_get_value(obj) or "0")..&…...
SQLAlchemy 封装的工具类,数据库pgsql(数据库连接池)
1.SQLAlchemy是什么? SQLAlchemy 是 Python 著名的 ORM 工具包。通过 ORM,开发者可以用面向对象的方式来操作数据库,不再需要编写 SQL 语句。 SQLAlchemy 支持多种数据库,除 sqlite 外,其它数据库需要安装第三方驱动。…...

【Git】Git 基础
Git 基础 参考 Git 中文文档 — https://git-scm.com/book/zh/v2 1.介绍 Git 是目前世界上最先进的分布式版本控制系统,有这么几个特点: 分布式:是用来保存工程源代码历史状态的命令行工具保存点:保存点可以追溯源码中的文件…...

腾讯云AI绘画:探究AI创意与技术的新边界
目录 一、2023的“网红词汇”——AI绘画二、智能文生图1、智能文生图的应用场景2、风格和配置的多样性3、输入一段话,腾讯云AI绘画给你生成一张图4、文本描述生成图像,惊艳全场 三、智能图生图:重新定义图像美学1、智能图生图的多元应用场景2…...

离线数仓同步数据1
用户行为表数据同步 2.1.4 日志消费Flume测试 [gpbhadoop104 ~]$ cd /opt/module/flume/ [gpbhadoop104 flume]$ cd job/ [gpbhadoop104 job]$ rm file_to_kafka.confcom.atguigu.gmall.flume.interceptor.TimestampInterceptor$Builder #定义组件 a1.sourcesr1 a1.channelsc1…...

c语言开篇---跟着视频学C语言
标识符 标识符必须声明定义,可以是变量、函数或其他实体。 Int是标识符吗? 不是,int是c语言关键词,不是随意命名的 C语言关键词如下: 常量 不需要被声明,不能赋值更改。 printf函数 printf是由print打印…...

本地yum源-如学
学不学? 如学~ 到底学不学? 如学~ 学? 如学~ 配置本地的镜像yum 使用到的 rpm 包 是根据centos8 里面自带的 在 /dev/cdrom 中包含着 一些系统自带的 rpm # 先将 /dev/cdrom 设备进行挂载 mkdir /up # 在…...
【实训】“宅急送”订餐管理系统(程序设计综合能力实训)
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》 🌝每一个不曾起舞的日子,都是对生命的辜负 前言 大一小学期,我迎来了人生中的第一次实训…...

openeuler上安装polarismesh集群
1、安装MySQL数据库 数据库连接地址10.10.10.168 用户root 密码123456 MySQL安装参考搭建DSS环境(六)之安装基础环境MySQL_linux安装dss_青春不流名的博客-CSDN博客 2、安装Redis集群 IPResid PORTSentinel PORTPASSWORDCluster NAME10.10.10.110637…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
