电子科技大学人工智能期末复习笔记(五):机器学习
目录
前言
监督学习 vs 无监督学习
回归 vs 分类 Regression vs Classification
训练集 vs 测试集 vs 验证集
泛化和过拟合 Generalization & Overfitting
线性分类器 Linear Classifiers
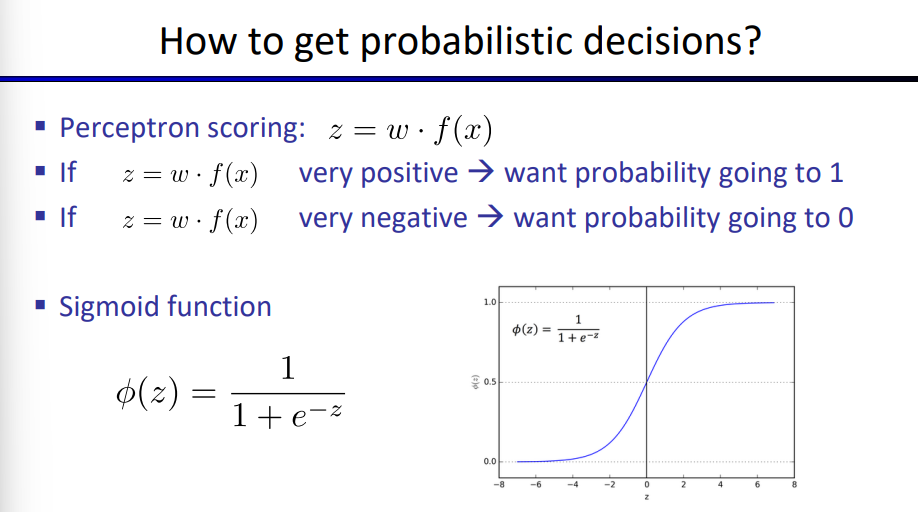
激活函数 - 概率决策
⚠线性回归
决策树 Decision Trees
决策树构建递归退出条件C
信息熵 Entropy
信息增益 Information Gain
⚠ID3算法实例
总结
前言
本复习笔记基于李晶晶老师的课堂PPT与复习大纲,供自己期末复习与学弟学妹参考用。
本节是人工智能复习的最后一小节,重点在于了解概念,会做计算题。
前面几节都在专栏当中,可以自行查看,也可以走传送门:
电子科技大学人工智能期末复习笔记(一):搜索问题
电子科技大学人工智能期末复习笔记(二):MDP与强化学习
电子科技大学人工智能期末复习笔记(三):一阶逻辑
电子科技大学人工智能期末复习笔记(四):概率与贝叶斯网络
监督学习 vs 无监督学习
监督学习:输入已知类别的数据样本 分类、回归
无监督学习:输入未知类别的数据样本 聚类
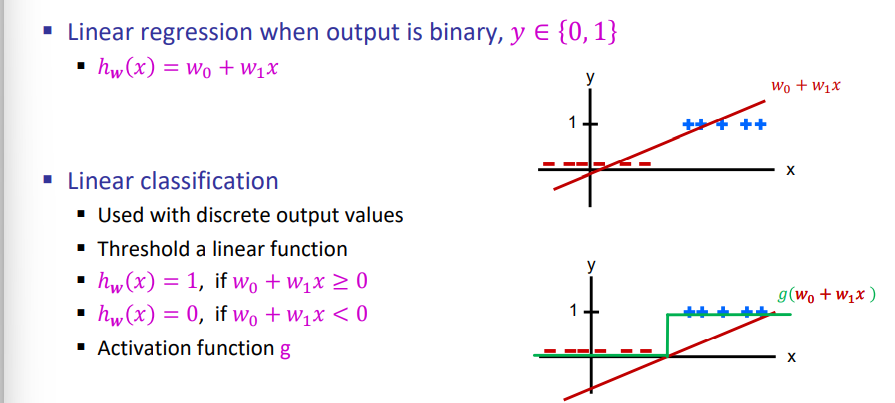
回归 vs 分类 Regression vs Classification
分类:对输入数据进行离散值标签的预测
回归:预测连续的、具体的数值
Output: 连续 vs 离散
分类需要激活函数
训练集 vs 测试集 vs 验证集
训练集用于学习参数(例如模型概率)
测试集用于计算模型的准确率
验证集用于调节超参数
泛化和过拟合 Generalization & Overfitting
在有监督学习中,我们会在训练数据集上建立一个模型,之后会把这个模型用于新的,之前从未见过的数据中,这个过程称为模型的泛化
模型在训练集上表现好,在测试集验证集表现差就说明出现了过拟合问题,出现这种情况的主要原因是训练数据中存在噪音或者训练数据太少
解决办法:选取合适的停止训练标准;使用验证数据集;获取额外数据进行交叉验证;正则化
Relative frequency parameters will overfit the training data
相对频率参数会过拟合训练数据
线性分类器 Linear Classifiers
输入特征向量 f(x)
权重向量 w
在二分类中:
真实标签为 y*∈{-1,1},
预测标签为 y ,w和f(x)在同一平面则为正样本,y=1,反之y=-1
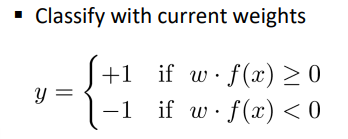
如果分类正确,不更新w,分类错误则更新 w
w = w + y* · f(x) 其中y* = 1或-1
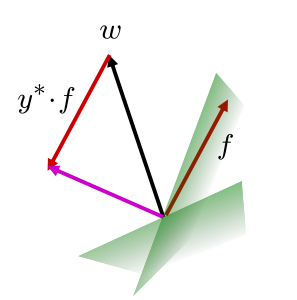
在多分类中:
输入特征向量 f(x)
每个类别的权重 向量 ![]()
预测标签为 y ,取![]() 最大的一个类别标签
最大的一个类别标签
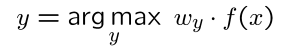
如果分类正确,不更新w;分类错误则更新 w,此时需要分别对正确和错误的两个w进行更新
关键点:减小错分类别的向量点积,增大真实类别的向量点积

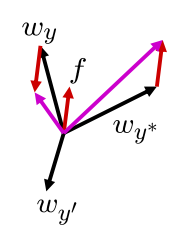
激活函数 - 概率决策
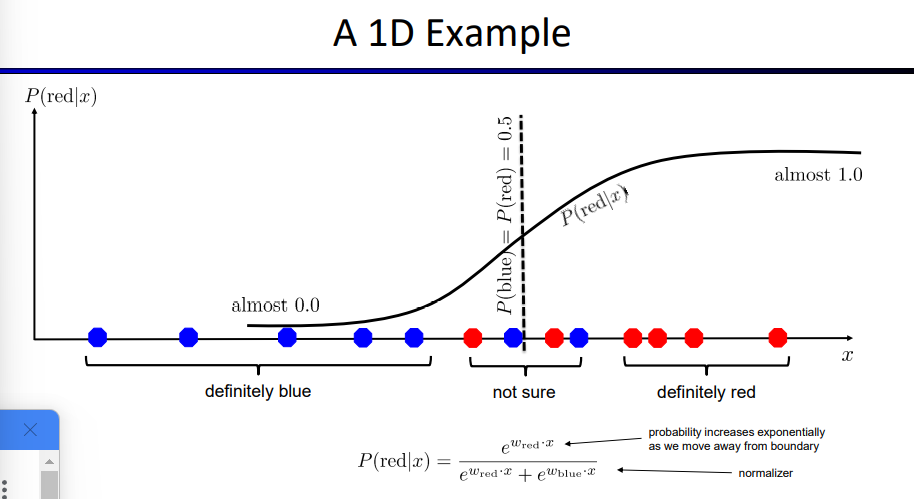
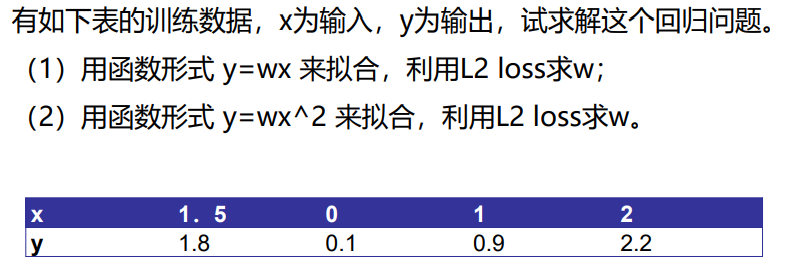
⚠线性回归
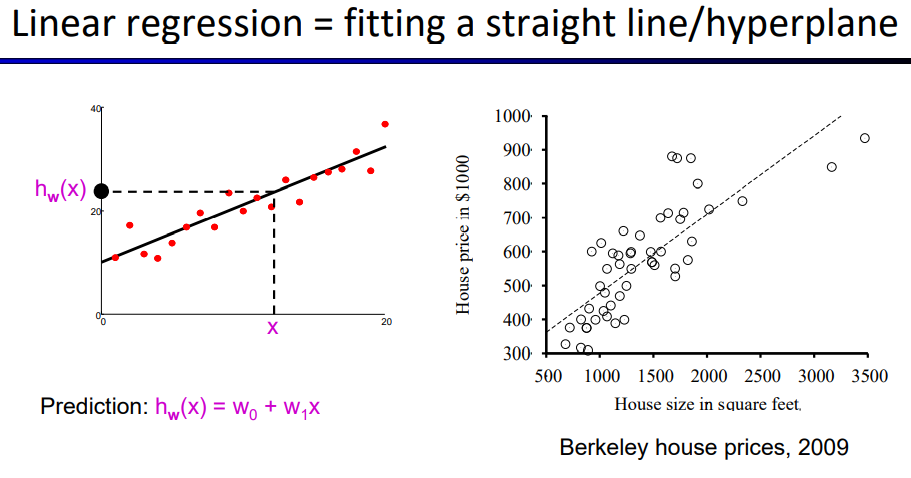

L2 loss:所有样本的平方误差和
![]()
例:

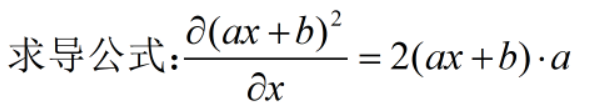
决策树 Decision Trees
决策树构建递归退出条件C
- 当前样本集D包含的样本属于同一类别C
- 当前属性集A为空或样本集D中所有样本在所有属性上取值相同(但类别可能不相同)
- 当前结点包含的样本集
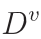 为空
为空
信息熵 Entropy
信息熵是度量样本集合纯度的指标
假定当前样本集合D中第k类样本所占比例为pk(k=1,2,...,|y|)则D的信息熵的定义为:
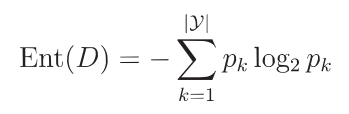
Ent(D)的取值范围为 [0,log2|y| ],值越小,纯度越高
计算信息熵时约定:若p=0,则![]() =0
=0
信息增益 Information Gain
样本集D的某个离散属性a有V个可能的取值![]() ,用a来对D进行划分则会产生V个分支结点,其中第v个分支结点包含了D中所有在在属性a上取值为
,用a来对D进行划分则会产生V个分支结点,其中第v个分支结点包含了D中所有在在属性a上取值为![]() 的样本,记为
的样本,记为![]() 。定义用属性a对样本集D进行划分所获得的信息增益为:
。定义用属性a对样本集D进行划分所获得的信息增益为:

一般而言,信息增益越大,意味着使用属性a来进行划分获得的纯度提升越大
在ID3算法中选择信息增益大的属性来划分样本集
⚠ID3算法实例
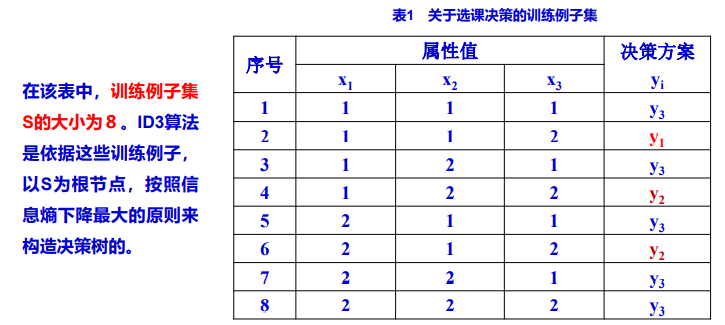





总结
至此人工智能复习笔记更新完毕,后续有时间会更新一下实验的讲解,包括基于A*算法的八数码问题求解、ID3决策树实战、以及Q-learning和Sarsa实现的悬崖问题求解。
相关文章:

电子科技大学人工智能期末复习笔记(五):机器学习
目录 前言 监督学习 vs 无监督学习 回归 vs 分类 Regression vs Classification 训练集 vs 测试集 vs 验证集 泛化和过拟合 Generalization & Overfitting 线性分类器 Linear Classifiers 激活函数 - 概率决策 ⚠线性回归 决策树 Decision Trees 决策树构建递归…...
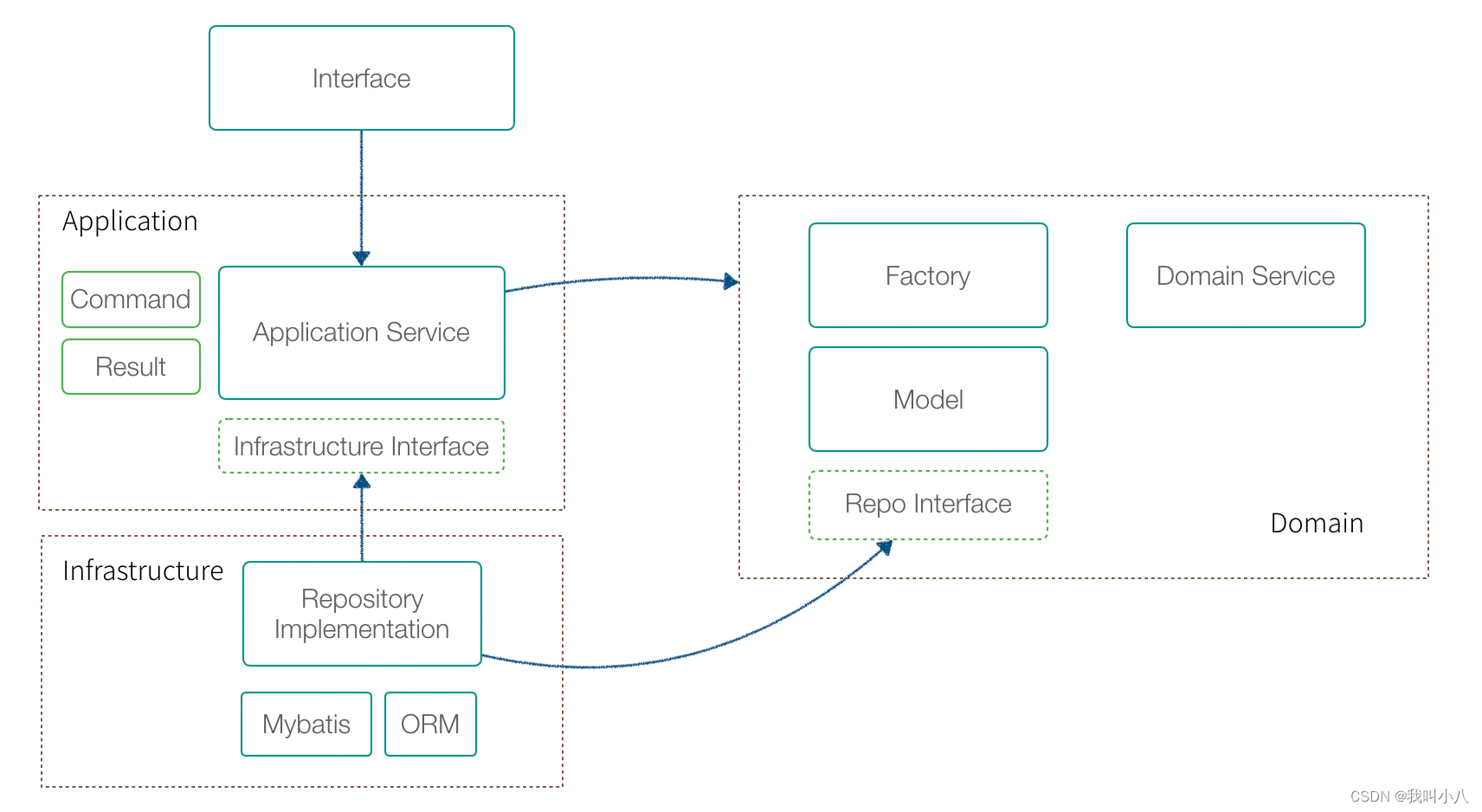
使用DDD指导业务设计的总结思考
领域驱动设计(DDD) 是 Eric Evans 提出的一种软件设计方法和思想,主要解决业务系统的设计和建模。DDD 有大量难以理解的概念,尤其是翻译的原因,某些词汇非常生涩,例如:模型、限界上下文、聚合、…...

面试官问:如何确保缓存和数据库的一致性?
如果你对这个问题有过研究,应该可以发现这个问题其实很好回答,如果第一次听到或者第一次遇到这个问题,估计会有点懵,今天我们来聊聊这个话题。 1、问题分析 首先我们来看看为什么会有这个问题! 我们在日常开发中&am…...

16.数据库Redis
一、基本概念 Redis(Remote Dictionary Server)译为“远程字典服务”,它是一款基于内存实现的键值型 NoSQL 数据库, 通常也被称为数据结构服务器,这是因为它可以存储多种数据类型,比如 string(字…...

【Redis高级-集群分片】
单机安装Redis首先需要安装Redis所需要的依赖:yum install -y gcc tclRedis安装包上传到虚拟机的任意目录:我放到了/tmp目录:解压缩:tar -zxvf /tmp/redis-6.2.4.tar.gz -C /tmp解压后:进入redis目录:cd /t…...

CSDN - CSDN27题解
文章目录幸运数字题目描述解题思路AC代码投篮题目描述解题思路AC代码通货膨胀-x国货币题目描述解题思路AC代码最后一位题目描述解题思路AC代码CSDN编程竞赛报名地址:https://edu.csdn.net/contest/detail/41 这次题目描述刚开始好像有些问题,之后被修正了…...

docker拉取mysql
搜索mysql版本docker search mysql搜索获赞数(星星数量) 大于 1000 的镜像docker search --filterstars1000 mysql搜索官方发布的版本docker search --filter is-officialtrue mysql搜索版本号docker search mysql57拉取docker pull devbeta/mysql57查看下载镜像docker images启…...

在Linux上安装Python3
记录:373场景:在CentOS 7.9操作系统上,安装Python-3.8.9环境。版本:JDK 1.8 Python-3.8.9官网地址:https://www.python.org下载地址:https://www.python.org/ftp/python/1.安装基础依赖1.1安装gcc(1)安装命…...

23 种设计模式的通俗解释,看完秒懂
01 工厂方法 追 MM 少不了请吃饭了,麦当劳的鸡翅和肯德基的鸡翅都是 MM 爱吃的东西,虽然口味有所不同,但不管你带 MM 去麦当劳或肯德基,只管向服务员说「来四个鸡翅」就行了。麦当劳和肯德基就是生产鸡翅的 Factory 工厂模式&…...
如何做好需求管理?经验方法、模型、工具
需求管理能力是衡量产品经理能力的一个重要指标。因为需求是产品的基石,只有选取恰当的方法进行需求分析及管理,才能更好的构建产品方案,从而输出精准的产品定义。结合本人学习和自身经验,打算将需求管理分”需求挖掘”、”需求分…...
)
怎么用期货做风险对冲(如何利用期货对冲风险)
不同期货市场的同一期货品种的对冲交易怎么做 不同 期货市场 的同一期货品种的 对冲交易 。 因为地域和 制度环境 不同,同一种期货品种在不同市场的同一时间的价格很可能是不一样的,并且也是在不断变化的。 这样在一个市场做多头买进࿰…...

C++标准模板库type_traits源码剖析
一、type_traits源码介绍 1、type_traits是C11提供的模板元基础库。 2、type_traits可实现在编译期计算。包括添加修饰、萃取、判断查询、类型推导等等功能。 3、type_traits提供了编译期的true和false。 二、type_traits的作用 1、根据不同类型,模板匹配不同版本…...

Python获取公众号(pc客户端)数据,使用Fiddler抓包工具
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 今天来教大家如何使用Fiddler抓包工具,获取公众号(PC客户端)的数据。 Fiddler是一个http协议调试代理工具,它能够记录并检查所有你的电脑和互联网之间的http通讯,…...
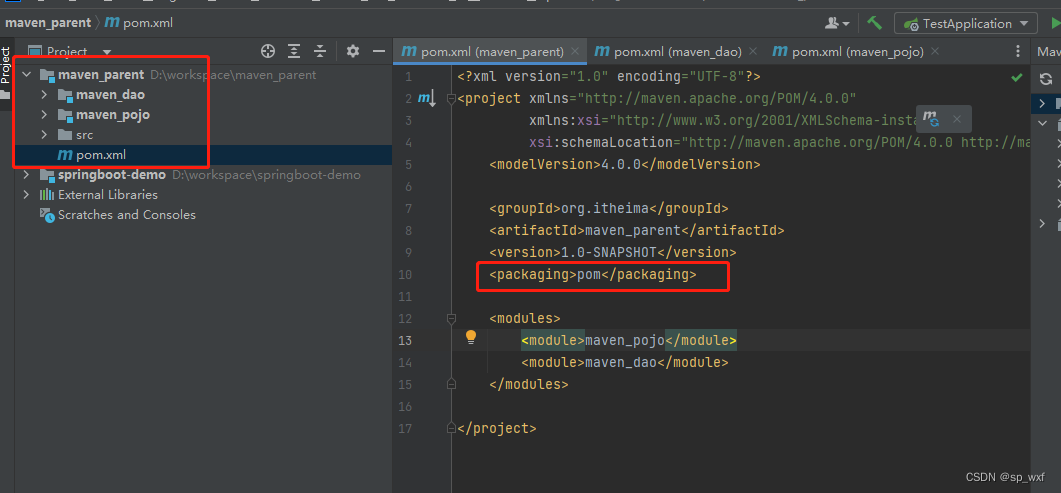
Maven进阶
这里写目录标题1.分模块开发1.1 模块更新后,会造成的影响2.依赖管理2.1 依赖传递2.2 可选依赖(隐藏自己的依赖,不让别人用)2.3 排除依赖(用别人的资源,把不用的去了)3.聚合与继承3.1 为什么要使用聚合工程?3.2 聚合工程开发2.1 聚合工程三级目录1.分模块开发 我们之前做的项目…...
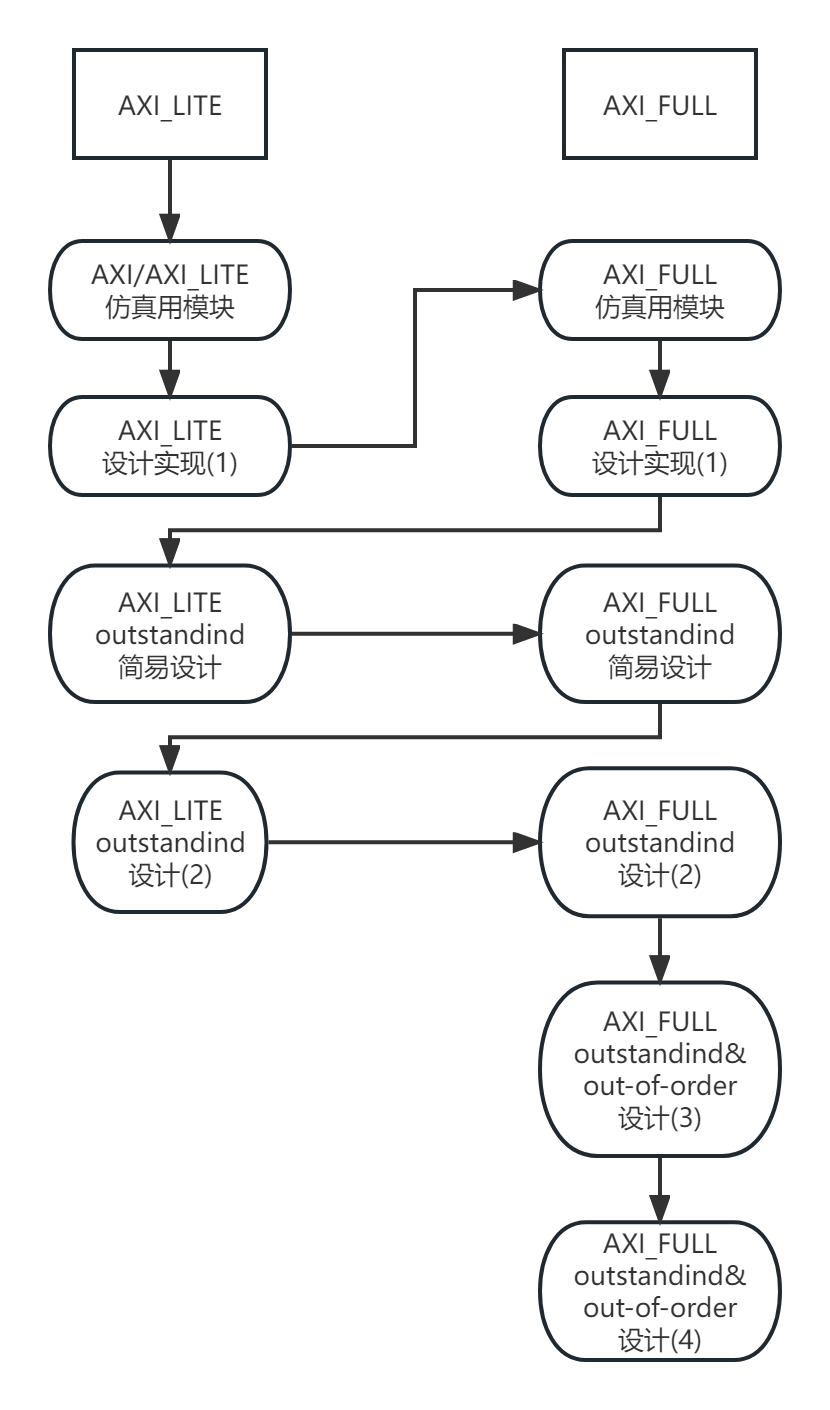
AXI实战(一)-为AXI总线搭建简单的仿真测试环境
AXI实战(一)-搭建简单仿真环境 看完在本文后,你将可能拥有: 一个可以仿真AXI/AXI_Lite总线的完美主端(Master)或从端(Slave)一个使用SystemVerilog仿真模块的船信体验小何的AXI实战系列开更了,以下是初定的大纲安排: 欢迎感兴趣的朋友关注并支持,以下为正文部分 文章目录…...
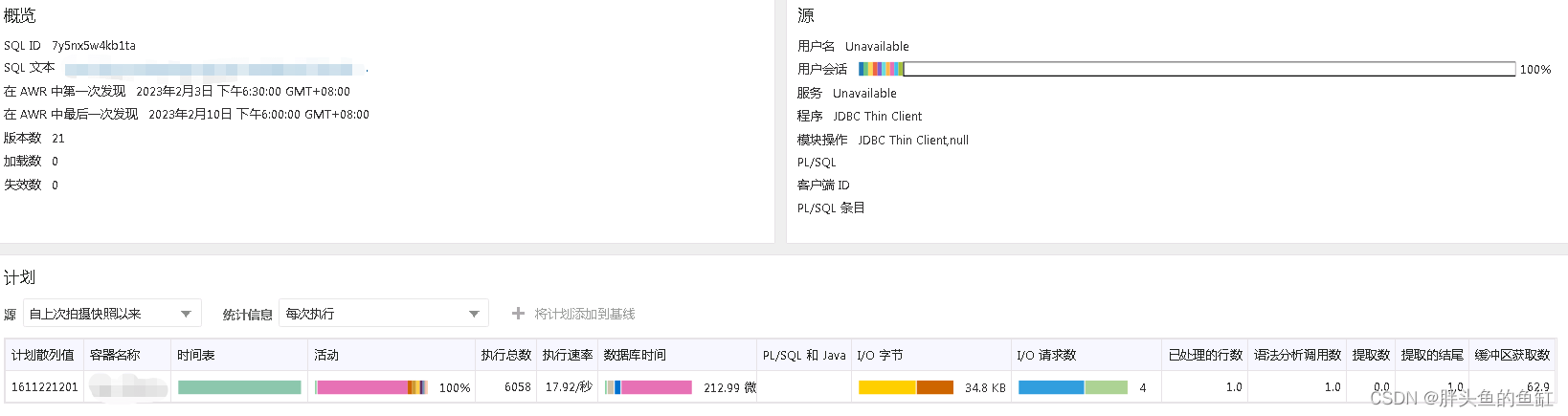
数据库管理-第五十六期 监控(20230210)
数据库管理 2023-02-10第五十六期 监控1 怎么监控2 直观3 历史分析4 另一个BUG总结第五十六期 监控 春节后的7天班过后就来到了2月份,本周对之前发现X8M上的那个bug进行补丁修复和协助从12.2迁移了一套PDB到这个一体机上面,2次割接。这周还和原厂老大哥…...
测试开发,测试架构师为什么能拿50 60k呢需要掌握哪些技能呢
这篇文章是软件工程系列知识总结的第五篇,同样我会以自己的理解来阐述软件工程中关于架构设计相关的知识。相比于我们常见的研发架构师,测试架构师是近几年才出现的一个岗位,当然岗位title其实没有特殊的含义,在我看来测试架构师其…...

Miniblink 入门
miniblink官网:入门之前强烈建议将Miniblink介绍仔细看一遍。 MB内核组件标准版接口文档:这里列举了所有的api以及简单的说明,但是本人建议还是看wke.h更方便,里面都是宏实现的,直接搜相关函数即可。 mb demo下载和参…...
[python入门㊷] - python存储数据
目录 ❤ json.dump()存储数据 ❤ json.laod()读取数据 ❤ 保存和读取用户生成的数据 ❤ 重构 JSON(JavaScript Object Notation)格式最初是为JavaScript开发的,但随后成了一种常见格式,被包括Python在内的众多语言采用 ❤ json.dump()存储数据…...

Little Fighter:旺角——NFT 系列来袭!
《小朋友齐打交 2 (LF2) 》是一款流行的格斗游戏,由 Marti Wong 和 Starsky Wong 于 1999 年创作。这是一款非常容易上瘾的游戏,具有多种游戏模式、横向卷轴格斗系统以及 24 个具有复杂动作和连击的不同角色。这款游戏在世界范围内非常受欢迎,…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
