七大排序算法
目录
直接插入排序
希尔排序
直接选择排序
堆排序
冒泡排序
快速排序
快速排序优化
非递归实现快速排序
归并排序
非递归的归并排序
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作.
常见的排序算法有插入排序(直接插入排序和希尔排序),选择排序(选择排序和堆排序),交换排序(冒泡排序和快速排序)以及归并排序.
我们将从时间复杂度,空间复杂度,以及排序的稳定性来分析这七大排序.
排序的稳定性
假定在待排序的记录序列中,存在多个具有相同关键字的记录,若经过排序,这些记录的相对次序保持不变,则称这种排序是稳定的.
直接插入排序
基本思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到 一个新的有序序列 。
public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (; j >= 0 ; j--) {if (array[j] > tmp){array[j+1] = array[j];}else {break;}}array[j+1] = tmp;}}时间复杂度:考虑最坏的情况下,就是全逆序的时候,此时时间复杂度为O(N^2).
最好的情况下,有序的时候,此时时间复杂度为O(N).得出一个结论:当数据量不多,且数据基本上是趋于有序的时候,此时直接插入排序是非常快的.
空间复杂度:O(1)
稳定性:稳定.一个本身就稳定的排序,可以实现为不稳定的排序;但是一个本身不稳定的排序,不能实现为稳定的排序.
希尔排序
希尔排序(缩小增量排序)是直接插入排序的一个优化.
基本思想:先将数据进行分组,将每一组内的数据先进行排序(这一过程叫做预排序);逐渐缩小组数,直到最后整体看作是一组,采用直接插入排序进行排序.
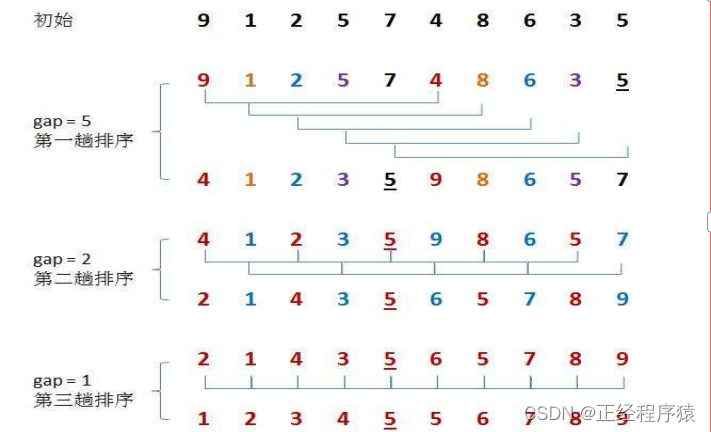
跳着分组的原因:尽可能的使小的数据靠前,大的数据靠后,从而使整体更加趋于有序.
public static void shellSort(int[] array){int gap = array.length;while (gap > 1){gap /= 2;shell(array,gap);}}private static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i-gap;for (; j >= 0 ; j-=gap) {if (array[j] > tmp){array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}}当gap>1时,都是预排序,目的是让数组更接近于有序.当gap==1时,此时数组已经接近有序了,这样进行插入排序就会很快.
希尔排序的时间复杂度不好计算,因为gap的取值方法有很多,导致很难去计算.目前还没有证明gap具体取多少是最快的.
时间复杂度:O(N^1.3),估计的时间复杂度.
空间复杂度:O(1)
稳定性:不稳定.
直接选择排序
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放到序列的起始位置,直到全部排序的数据元素排完.
public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i+1; j < array.length; j++) {if (array[minIndex] > array[j]){minIndex = j;}}//处理两个下标一样的情况if (i != minIndex) {int tmp = array[i];array[i] = array[minIndex];array[minIndex] = tmp;}}}直接选择排序好理解,但是效率低下.
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:不稳定
堆排序
排升序要建大堆,排降序建小堆.
升序,建大堆:堆顶元素和最后一个元素交换,将数组长度-1,在对堆顶元素进行向下调整,依次循环.
public static void heapSort(int[] array){createBigHeap(array);int end = array.length-1;while(end > 0){swap(array,0,end);shiftDown(array,0,end);end--;}}//建立大根堆//从最后一颗子树的根节点开始,每一次都进行向下调整private static void createBigHeap(int[] array){for (int parent = (array.length-1-1)/2; parent >=0 ; parent--) {shiftDown(array,parent,array.length);}}//向下调整private static void shiftDown(int[] array,int parent,int len){int child = (2*parent)+1;while (child < len){if (child+1 < len && array[child] < array[child+1]){child++;}if (array[child] > array[parent]){swap(array,child,parent);parent = child;child = (2*parent)+1;}else {break;}}}public static void swap(int[] array,int x,int y){int tmp = array[x];array[x] = array[y];array[y] = tmp;}时间复杂度:O(n*logn)
空间复杂度:O(1)
稳定性:不稳定
冒泡排序
相邻元素之间的比较.
public static void bubbleSort(int[] array){//最外层控制的是趟数//五个数据需要比较四趟for (int i = 0; i < array.length-1; i++) {//加一个标志对冒泡排序进行优化boolean flg = false;for (int j = 0; j < array.length - 1 - i; j++) {if (array[j] > array[j+1]){swap(array,j,j+1);flg = true;}}if (flg == false){break;}}}时间复杂度:(不考虑优化)O(n^2)
空间复杂度:O(1)
稳定性:稳定
快速排序
public static void quickSort(int[] array){quick(array,0,array.length-1);}public static void quick(int[] array,int start,int end){//大于号 是预防1 2 3 4 5 6,直接没有左树或没有右树if (start >= end){return;}int pivot = partition(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}//找基准//Hoare版本private static int partition(int[] array,int left,int right){int i = left;int pivot = array[left];while (left < right){while (left < right && array[right] >= pivot){right--;}//right下标的值小于pivotwhile (left < right && array[left] <= pivot){left++;}//left下标的值大于pivotswap(array,left,right);}//循环走完,left和right相遇//交换 和原来的leftswap(array,left,i);//返回基准return left;}时间复杂度:O(n*logn)
此时间复杂度不是最坏情况下的时间复杂度,最坏情况下是有序的情况下,此时树的高度是n,时间复杂度是O(n^2),空间复杂度也变成了O(n).
空间复杂度:O(logn)
稳定性:不稳定
挖坑法找基准
private static int partition(int[] array,int left,int right){int pivot = array[left];while (left < right){while (left < right && array[right] >= pivot){right--;}array[left] = array[right];while (left < right && array[left] <= pivot){left++;}array[right] = array[left];}array[left] = pivot;//返回基准return left;}挖坑法是找到合适的值直接交换.
需要注意的是挖坑法和hoare找基准的结果是不一样的但是最终都是有序的.
快速排序优化
当数据有序的时候,快速排序的时间复杂度达到最大,而且空间复杂度也会随之改变.
三数取中法
为了使二叉树的划分尽可能的均匀,我们在left,mid,right三个数中,取出中间大的值,来作为key(left).
比如1 2 3 4 5,如果不采用三数取中法,那么1作为key走下来,left和right在1相遇,基准就是1,此时划分的就是单分支的树;如果采用三数取中,将数组顺序调整为 3 2 1 4 5,3作为key,走下来,left和right在中间位置相遇,将3和1交换,变为 1 2 3 4 5,虽然又变回去了,但是此时的基准在中间位置3的地方,此时二叉树划分的将更加均匀.
public static void quick(int[] array,int start,int end){//大于号 是预防1 2 3 4 5 6,直接没有左树或没有右树if (start >= end){return;}//在找基准之前,进行三数取中的优化,尽量去解决划分不均匀的问题.//在left,mid,right三个数中找到中间大的数字做keyint index = findMidValueOfIndex(array, start, end);swap(array,start,index);int pivot = partitionHoare(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);}//3个数中取中位数private static int findMidValueOfIndex(int[] array,int start,int end){int minIndex = (start+end)/2;if (array[start] > array[end]){if (array[minIndex] > array[start]){return start;}else if (array[minIndex] < array[end]){return end;}else {return minIndex;}}else {if (array[minIndex] > array[end]){return end;}else if (array[minIndex] < array[start]){return start;}else {return minIndex;}}}我们除了采取这种优化之外,还可以在快速排序递归到小区间的时候,采用插入排序.
因为插入排序在数据趋于有序并且数据量小的时候,排序的速度非常快.
非递归实现快速排序
public static void quickSort2(int[] array) {Stack<Integer> stack = new Stack<>();int start = 0;int end = array.length-1;int pivot = partition(array,start,end);//1.判断左边是不是有2个元素if(pivot > start+1) {stack.push(start);stack.push(pivot-1);}//2.判断右边是不是有2个元素if(pivot < end-1) {stack.push(pivot+1);stack.push(end);}while (!stack.isEmpty()) {end = stack.pop();start = stack.pop();pivot = partition(array,start,end);//3.判断左边是不是有2个元素if(pivot > start+1) {stack.push(start);stack.push(pivot-1);}//4.判断右边是不是有2个元素if(pivot < end-1) {stack.push(pivot+1);stack.push(end);}}归并排序
先分解,后合并.
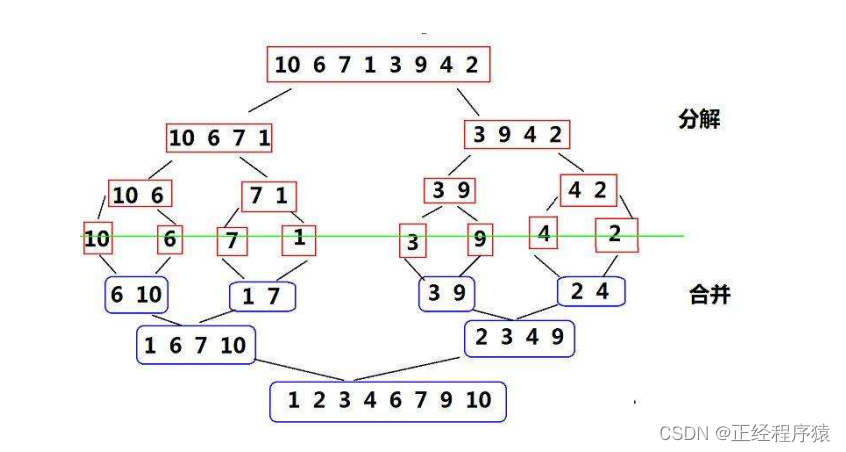
public static void mergeSort1(int[] array) {mergeSortChild(array,0,array.length-1);}private static void mergeSortChild(int[] array,int left,int right) {if(left == right) {return;}int mid = (left+right) / 2;mergeSortChild(array,left,mid);mergeSortChild(array,mid+1,right);//合并merge(array,left,mid,right);}private static void merge(int[] array,int left,int mid,int right) {int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;int[] tmpArr = new int[right-left+1];int k = 0;//表示tmpArr 的下标while (s1 <= e1 && s2 <= e2) {if(array[s1] <= array[s2]) {tmpArr[k++] = array[s1++];}else{tmpArr[k++] = array[s2++];}}while (s1 <= e1) {tmpArr[k++] = array[s1++];}while (s2 <= e2) {tmpArr[k++] = array[s2++];}//tmpArr当中 的数据 是right left 之间有序的数据for (int i = 0; i < k; i++) {array[i+left] = tmpArr[i];}}时间复杂度:O(n*logn).
空间复杂度:O(n)
稳定性:稳定
非递归的归并排序
public static void mergeSort(int[] array) {int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i += gap*2) {int left = i;int mid = left + gap -1;int right = mid+gap;if(mid >= array.length) {mid = array.length-1;}if(right >= array.length) {right = array.length-1;}merge(array,left,mid,right);}gap *= 2;}}相关文章:

七大排序算法
目录 直接插入排序 希尔排序 直接选择排序 堆排序 冒泡排序 快速排序 快速排序优化 非递归实现快速排序 归并排序 非递归的归并排序 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作. 常见的排序算法有插入排序(直接插入…...

GitHub two-factor authentication
1. 介绍 登录 GitHub 官网,会提示要开启双因子认证。 但推荐的 APP 都是国外了,国内用不了。 可以使用 “腾讯身份验证器” 微信小程序。 2. 操作 开启双因子认证: 打开 “腾讯身份验证器” 微信小程序,扫描 GitHub 那个二维…...
un-app-手机号授权登录-授权框弹不出情况
前言 手机号授权是获取用户信息api停用之后,经常使用的api。但是此api也是有很多坑 手机号授权会出现调用不起来的情况,这是因为小程序后台没有进行微信认证导致的 手机号授权调用不起来-没有微信认证 来到小程序后台-设置-基本设置-下拉找到微信认证…...

手写Spring:第14章-自动扫描Bean对象注册
文章目录 一、目标:自动扫描Bean对象注册二、设计:自动扫描Bean对象注册三、实现:自动扫描Bean对象注册3.0 引入依赖3.1 工程结构3.2 Bean生命周期中自动加载包扫描注册Bean对象和设置占位符属性类图3.3 主力占位符配置3.4 定义拦截注解3.4.1…...

redux中间件的简单讲解
redux中间件 中间件的作用: 就是在 源数据 到 目标数据 中间做各种处理,有利于程序的可拓展性,通常情况下,一个中间件就是一个函数,且一个中间件最好只做一件事情 数据源 --------> 中间件 --------> 中间件 -…...

嵌入式开发-绪论
目录 一.什么是嵌入式 1.1硬件系统 1.2软件系统 二.嵌入式应用场景 2.1消费电子 2.1.1智能家居 2.1.2影音 2.1.3家用电器 2.1.4玩具游戏机 2.2通信领域 2.2.1对讲机 2.2.2手机 2.2.3卫星 2.2.4雷达 2.3控制领域 2.3.1机器人 2.3.2采集器PLC 2.4金融 2.4.1POS…...

大数据知识合集之预处理方法
数据预处理方法主要有: 数据清洗、数据集成、数据规约和数据变换。 1、数据清洗 数据清洗(data cleaning) :是通过填补缺失值、光滑噪声数据,平滑或删除离群点,纠正数据的不一致来达到清洗的目的。 缺失值处理 实际开发获取信…...
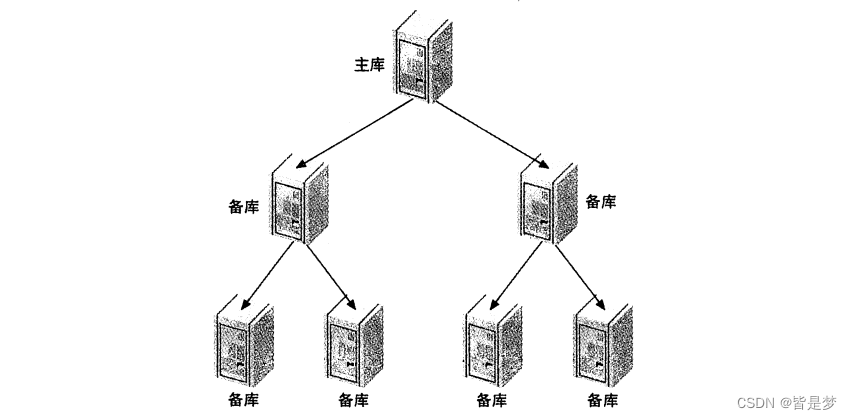
mysql(九)mysql主从复制
目录 前言概述提出问题主从复制的用途工作流程 主从复制的配置创建复制账号配置主库和从库启动主从复制从另一个服务器开始主从复制主从复制时推荐的配置sync_binloginnodb_flush_logs_at_trx_commitinnodb_support_xa1innodb_safe_binlog 主从复制的原理基于语句复制优点&…...
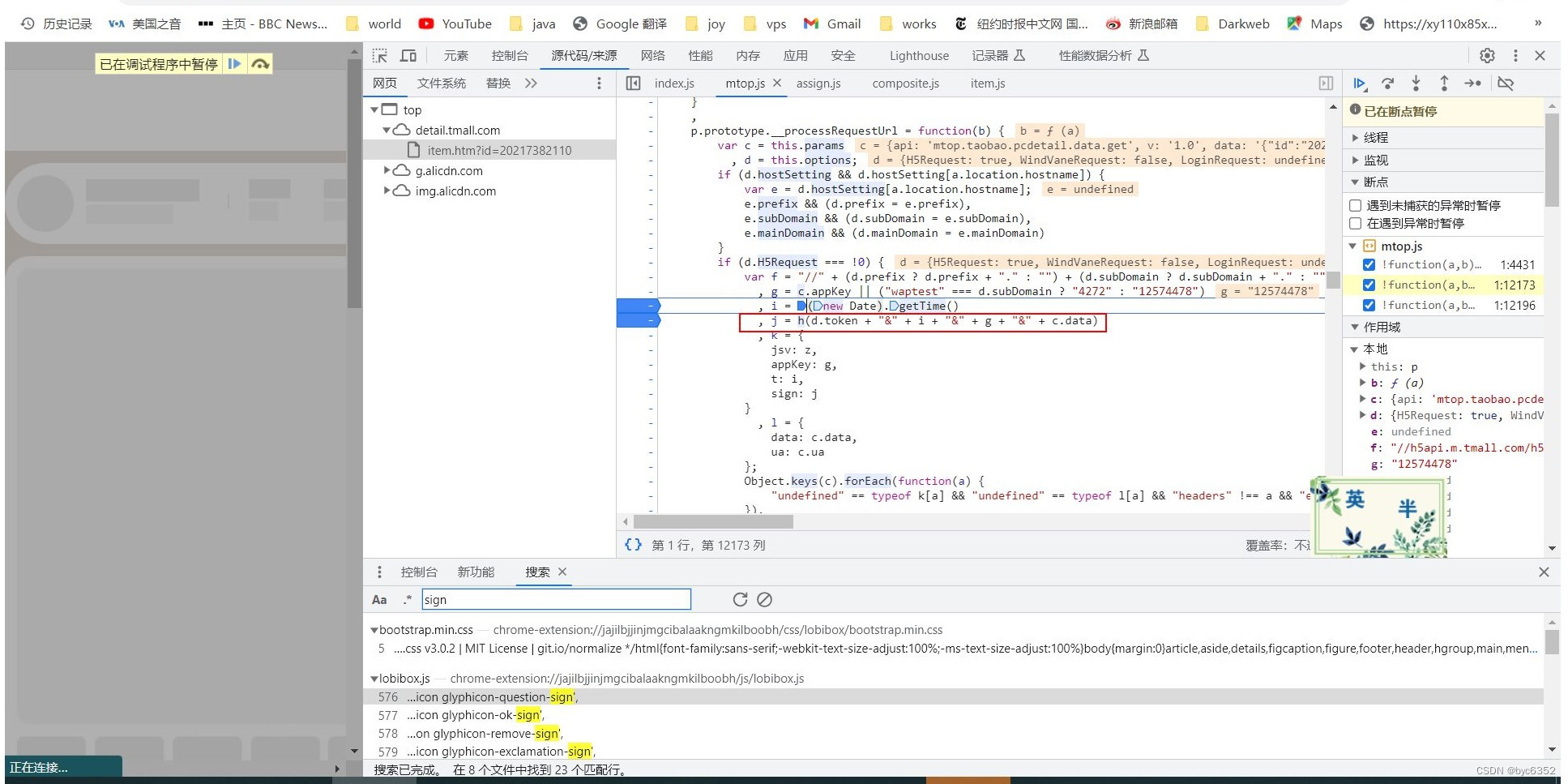
nodejs采集淘宝、天猫网商品详情数据以及解决_m_h5_tk令牌及sign签名验证(2023-09-09)
一、淘宝、天猫sign加密算法 淘宝、天猫对于h5的访问采用了和APP客户端不同的方式,由于在h5的js代码中保存appsercret具有较高的风险,mtop采用了随机分配令牌的方式,为每个访问端分配一个token,保存在用户的cookie中,通…...
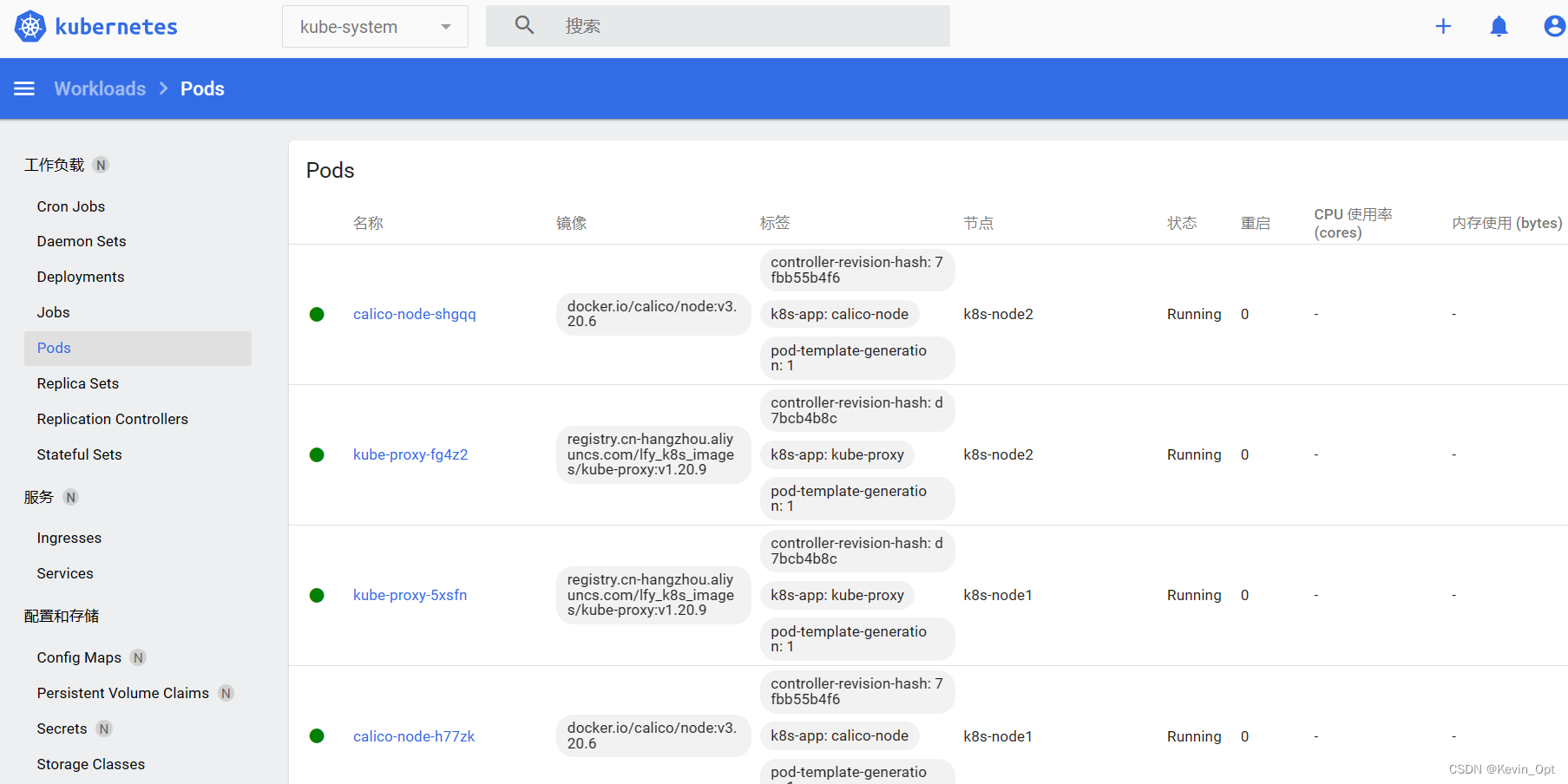
虚拟机上部署K8S集群
虚拟机上部署K8S集群 安装VM Ware安装Docker安装K8S集群安装kubeadm使用kubeadm引导集群 安装VM Ware 参考:http://www.taodudu.cc/news/show-2034573.html?actiononClick 安装Docker 参考:https://www.yuque.com/leifengyang/oncloud/mbvigg#2ASxH …...

设计模式 - 责任链
一、前言 相信大家平时或多或少都间接接触过责任链设计模式,只是可能有些同学自己不知道此处用的是该设计模式,比如说 Java Web 中的 Filter 过滤器,就是非常经典的责任链设计模式的例子。 那么什么是责任链设计模式呢? …...
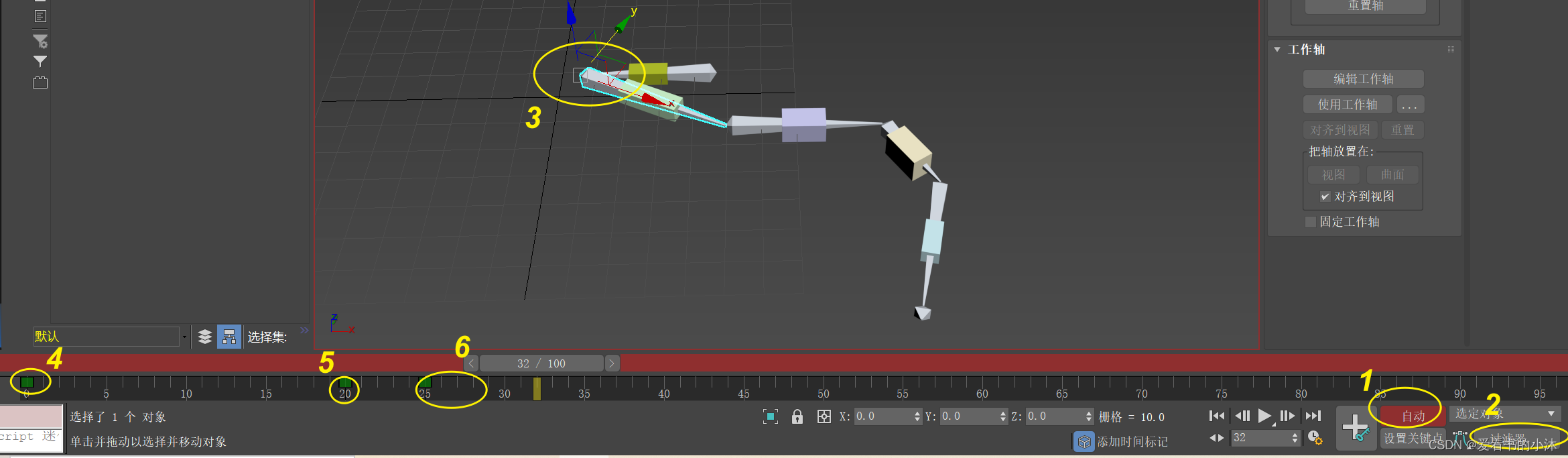
【小沐学Unity3d】3ds Max 骨骼动画制作(CAT、Character Studio、Biped、骨骼对象)
文章目录 1、简介2、 CAT2.1 加载 CATRig 预设库2.2 从头开始创建 CATRig 3、character studio3.1 基本描述3.2 Biped3.3 Physique 4、骨骼系统4.1 创建方法4.2 简单示例 结语 1、简介 官网地址: https://help.autodesk.com/view/3DSMAX/2018/CHS https://help.aut…...
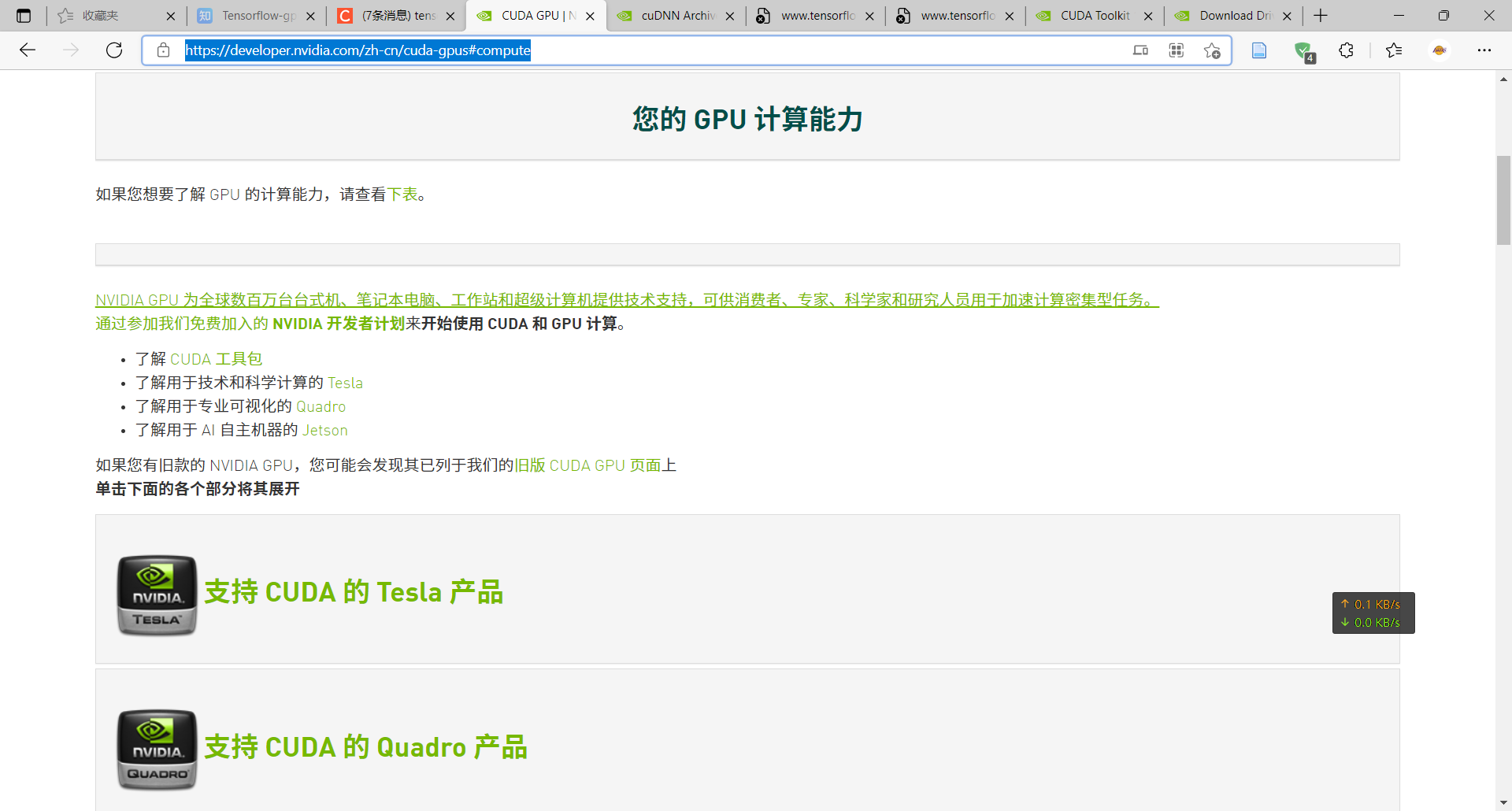
CUDA说明和安装[window]
文章目录 1、查看版本信息查看GPU查看cuda版本其他方法 2区分 了解cudaCUDA ToolkitNVCCcuDNN 3/ 安装过程4/版本的问题CUDA Toolkit和 显卡驱动 的版本对应CUDA / CUDA Toolkit和cuDNN的版本对应 5/关于CUDA和Cudnn**5.1 CUDA的命名规则****5.2 如何查看自己所安装的CUDA的版本…...
sqlserver2012性能优化配置:设置性能相关的服务器参数
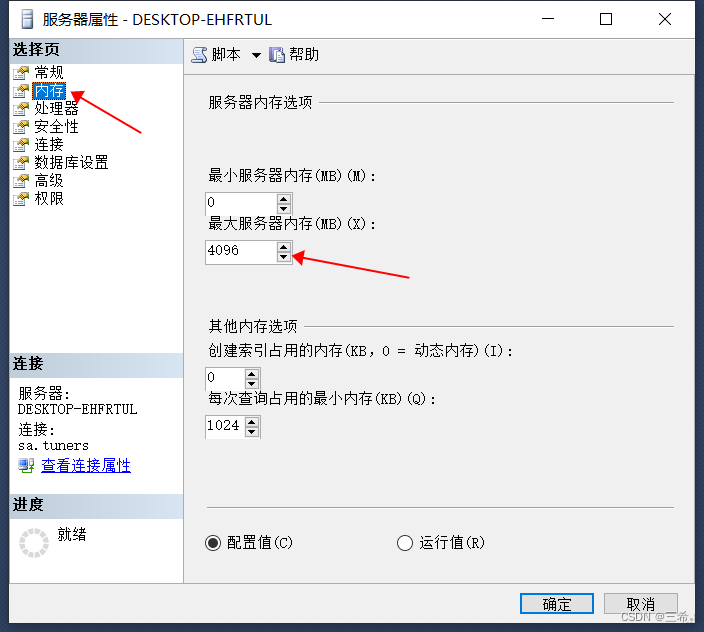
前言 sqlserver2012 长时间运行的话会将服务器的内存占满 解决办法 通过界面设置 下图中设置最大服务器内存 通过执行脚本设置 需要先开发开启高级选项配置才能设置成功 设置完成之后将高级选择配置关闭,还原成跟之前一样 --可以配置高级选项 EXEC sp_conf…...
介绍 dubbo-go 并在Mac上安装,完成一次自己定义的接口RPC调用
目录 RPC 远程调用的说明作用:像调用本地方法一样调用远程方法和直接HTTP调用的区别:调用模型图示: Dubbo 框架说明Dubbo Go 介绍应用 Dubbo Go环境安装(Mac 系统)安装 Go语言环境安装 序列化工具protoc安装 dubbogo-c…...
)
目标检测数据集:摄像头成像吸烟检测数据集(自己标注)
1.专栏介绍 ✨✨✨✨✨✨目标检测数据集✨✨✨✨✨✨ 本专栏提供各种场景的数据集,主要聚焦:工业缺陷检测数据集、小目标数据集、遥感数据集、红外小目标数据集,该专栏的数据集会在多个专栏进行验证,在多个数据集进行验证mAP涨点明显,尤其是小目标、遮挡物精度提升明显的…...
Unity的UI管理器
1、代码 public class UIManager {private static UIManager instance new UIManager();public static UIManager Instance > instance;//存储显示着的面板脚本(不是面板Gameobject),每显示一个面板就存入字典//隐藏的时候获取字典中对…...

Mp4文件提取详细H.264和MP3文件
文章目录 Mp4文件提取为H.264和MP3文件**提取视频为H.264:****提取音频为MP3:** 点赞收藏加关注,追求技术不迷路!!!欢迎评论区互动。 Mp4文件提取为H.264和MP3文件 要将视频分开为H.264(视频编…...
Qt应用程序连接达梦数据库-飞腾PC麒麟V10
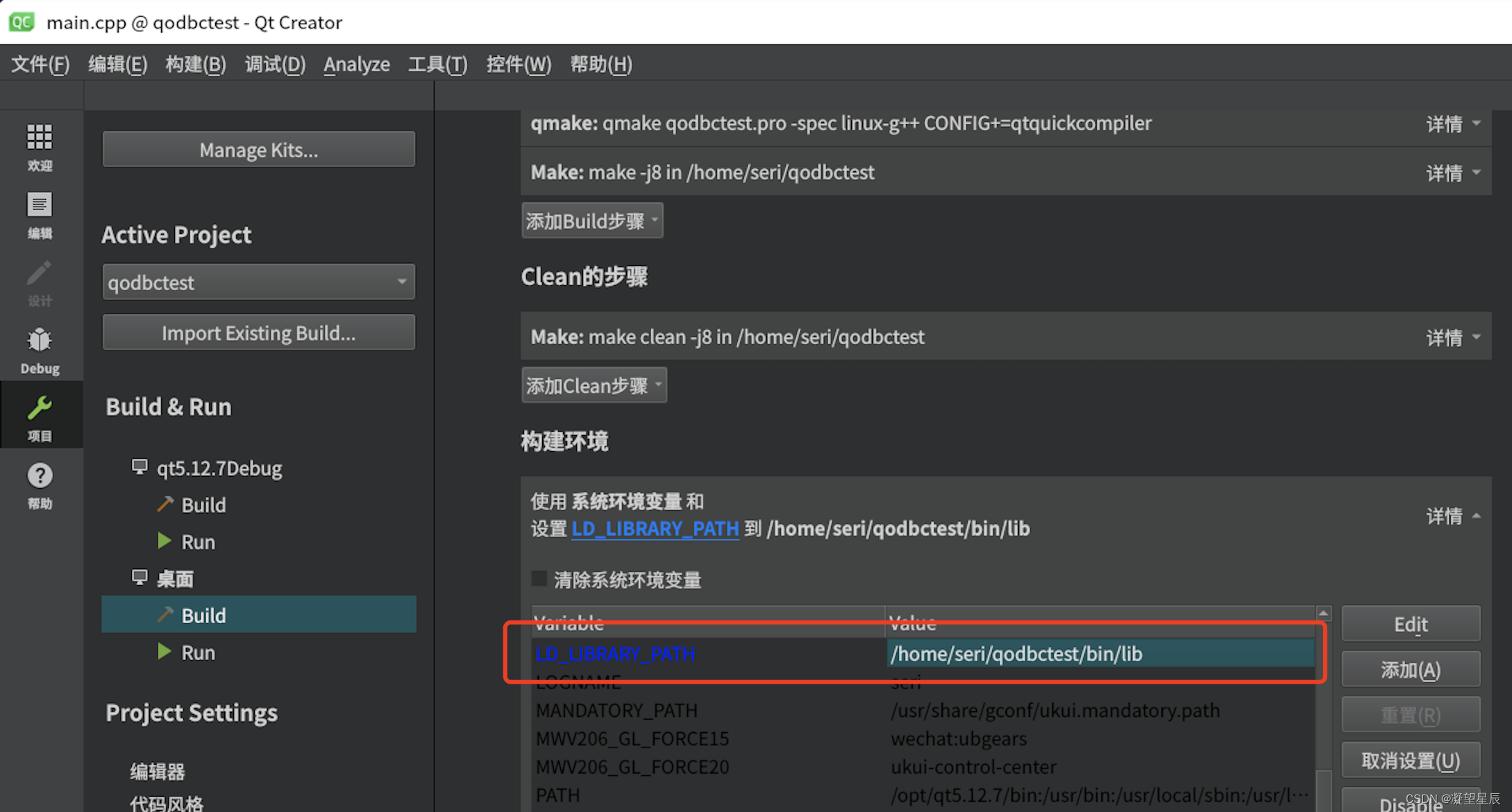
目录 前言1 安装ODBC1.1 下载unixODBC源码1.2 编译安装1.4 测试 2 编译QODBC2.1 修改 qsqldriverbase.pri 文件2.2 修改 odbc.pro 文件2.3 编译并安装QODBC 3 Qt应用程序连接达梦数据库测试4 优化ODBC配置,方便程序部署4.1 修改pro文件,增加DESTDIR 变量…...

2023-09-03 LeetCode每日一题(消灭怪物的最大数量)
2023-09-03每日一题 一、题目编号 1921. 消灭怪物的最大数量二、题目链接 点击跳转到题目位置 三、题目描述 你正在玩一款电子游戏,在游戏中你需要保护城市免受怪物侵袭。给你一个 下标从 0 开始 且长度为 n 的整数数组 dist ,其中 dist[i] 是第 i …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
