王道数据结构编程题 二叉树
二叉树定义
以下为本文解题代码的二叉树定义。
struct TreeNode {int val;TreeNode* left, *right;TreeNode(int val = 0, TreeNode* left = nullptr, TreeNode* right = nullptr): val(val), left(left), right(right) {}
};
非递归后序遍历
题目描述
编写后序遍历二叉树的非递归算法。
解题代码
void nonRecurPost(TreeNode* root) {if (root == nullptr) return;stack<TreeNode*> s;TreeNode* pre = nullptr;while (root != nullptr || !s.empty()) {while (root != nullptr) {s.emplace(root);root = root->left;}root = s.top();s.pop();if (root->right == nullptr || root->right == pre) {cout << root->val << " ";pre = root;root = nullptr;}else {s.emplace(root);root = root->right;}}
}
反向层序遍历
题目描述
试给出二叉树的自下而上、从右到左的层序遍历算法。
解题代码
void reOrderTraversal(TreeNode* root) {queue<TreeNode*> Q;stack<int> S;Q.emplace(root);while (!Q.empty()) {TreeNode* fNode = Q.front();S.emplace(fNode->val);Q.pop();if (fNode->left != nullptr) {Q.emplace(fNode->left);}if (fNode->right != nullptr) {Q.emplace(fNode->right);}}while (!S.empty()) {cout << S.top() << " ";S.pop();}
}
非递归计算高度
题目描述
假设二叉树采用二叉链表存储结构,设计一个非递归算法求二叉树的高度。
解题代码
int nonRecurHeight(TreeNode* root) {if (root == nullptr) return 0;int res = 0;queue<TreeNode*> q, nq;q.emplace(root);while (!q.empty()) {while (!q.empty()) {TreeNode* fNode = q.front();q.pop();if (fNode->left != nullptr) {nq.emplace(fNode->left);}if (fNode->right != nullptr) {nq.emplace(fNode->right);}}q = move(nq);++res;}return res;
}
根据中序和先序序列建立二叉树
题目描述
设一棵二叉树各结点的值互不相同,其先序遍历序列和中序遍历序列分别存储于两个一维数组 A 和 B 中,试编写算法建立该二叉树的二叉链表。
解题代码
TreeNode* recurCreate(vector<int>& preOrder, int l1, int r1, vector<int>& inOrder, int l2, int r2) {if (l1 == r1) return nullptr;auto preBegin = preOrder.begin() + l1, preEnd = preOrder.begin() + r1;auto inBegin = inOrder.begin() + l2, inEnd = inOrder.begin() + r2;int x = *preBegin;TreeNode* root = new TreeNode(x);auto it = find(inBegin, inEnd, x);int lenL = it - inBegin;root->left = recurCreate(preOrder, l1 + 1, l1 + lenL + 1, inOrder, l2, l2 + lenL);root->right = recurCreate(preOrder, l1 + lenL + 1, r1, inOrder, l2 + lenL + 1, r2);return root;}TreeNode* createTree(vector<int>& preOrder, vector<int>& inOrder) {int l1 = 0, r1 = preOrder.size();int l2 = 0, r2 = inOrder.size();return recurCreate(preOrder, l1, r1, inOrder, l2, r2);}
判断完全二叉树
题目描述
二叉树按二叉链表形式存储,试编写一个判别给定二叉树是否是完全二叉树的算法。
解题代码
bool isCompleteBT(TreeNode* root) {queue<TreeNode*> Q;Q.emplace(root);bool isLeaves = false;while (!Q.empty()) {TreeNode* fNode = Q.front();Q.pop();if (fNode == nullptr) {isLeaves = true;continue;}if (isLeaves) return false;Q.emplace(fNode->left);Q.emplace(fNode->right);}return true;
}
计算双分支结点数
题目描述
假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支结点个数。
解题代码
int doubleNodeCnt(TreeNode* root) {if (root == nullptr) return 0;if (root->left != nullptr && root->right != nullptr) {return 1 + doubleNodeCnt(root->left) + doubleNodeCnt(root->right);}else {return doubleNodeCnt(root->left) + doubleNodeCnt(root->right);}
}
交换左右子树
题目描述
设树 B 是一棵采用链式结构存储的二叉树,编写一个把树 B 中所有结点的左右子树进行交换的算法。
解题代码
void swapLRNode(TreeNode* root) {if (root == nullptr) return;TreeNode* temp = root->left;root->left = root->right;root->right = temp;swapLRNode(root->left);swapLRNode(root->right);
}
先序序列第k个结点值
题目描述
假设二叉树采用二叉链表存储结构,设计一个算法,求先序遍历序列中第 k (1 <= k <= 链表中结点个数)个结点的值。
解题代码
int kthNodeVal(TreeNode* root, int& k) {if (root == nullptr) return 0;if (--k == 0) return root->val;return kthNodeVal(root->left, k) + kthNodeVal(root->right, k);
}
删除特定值的结点的子树
题目描述
已知二叉树以二叉链表形式存储,编写算法完成:对于树中的每个元素值为 x 的结点,删除以它为根的子树,并释放相应的空间。
解题代码
void freeMemory(TreeNode* root) {if (root == nullptr) return;freeMemory(root->left);freeMemory(root->right);delete root;
}void deleteXNode(TreeNode* root, int x) {if (root == nullptr) return;else if (root->val == x) {freeMemory(root);return;}if (root->left != nullptr && root->left->val == x) {freeMemory(root->left);root->left = nullptr;}if (root->right != nullptr && root->right->val == x) {freeMemory(root->right);root->right = nullptr;}deleteXNode(root->left, x);deleteXNode(root->right, x);
}
值为x的结点的祖先
题目描述
在二叉树中查找值为 x 的结点,试编写算法打印值为 x 的结点的所有祖先,假设值为 x 的结点的不多于一个。
解题代码
bool ancestorOfXNode(TreeNode* root, int x) {if (root == nullptr) return false;if (root->val == x) return true;bool left = ancestorOfXNode(root->left, x);bool right = ancestorOfXNode(root->right, x);if (left || right) {cout << root->val << " ";}return left || right;
}
两结点的最近公共祖先
题目描述
设 p 和 q 为指向二叉树中任意两个结点的指针,试编写算法找到 p 和 q 的最近公共祖先结点 r.
解题代码
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == nullptr || root == p || root == q) return root;TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);if (left != nullptr && right != nullptr) {return root;}else if (left != nullptr) {return left;}else {return right;}
}
二叉树的宽度
题目描述
假设二叉树采用二叉链表存储结构,设计一个算法,求非空二叉树 b 的宽度(即具有结点数最多的那一层的结点个数)。
解题代码
int widthOfBT(TreeNode* root) {if (root == nullptr) return 0;size_t res = 1;queue<TreeNode*> q, nq;q.emplace(root);while (!q.empty()) {while (!q.empty()) {TreeNode* fNode = q.front();q.pop();if (fNode->left != nullptr) {nq.emplace(fNode->left);}if (fNode->right != nullptr) {nq.emplace(fNode->right);}}q = move(nq);res = max(res, q.size());}return res;
}
满二叉树的后序序列
题目描述
设有一棵满二叉树(所有结点值均不同),已知其先序序列为 pre,设计一个算法求其后序序列 post.
解题代码
void getPost(vector<int>& preOrder, int p1, int q1, vector<int>& postOrder, int p2, int q2) {if (p1 > q1) return;postOrder[q2] = preOrder[p1];int mid = (q1 - p1) / 2;getPost(preOrder, p1 + 1, p1 + mid, postOrder, p2, p2 + mid - 1);getPost(preOrder, p1 + mid + 1, q1, postOrder, p2 + mid, q2 - 1);
}vector<int> postOfFBT(vector<int>& preOrder) {int n = preOrder.size();vector<int> res(n);getPost(preOrder, 0, n - 1, res, 0, n - 1);return res;
}
将叶结点连接为单链表
题目描述
设计一个算法将二叉树的叶结点按从左到右的顺序连成一个单链表,表头指针为 head,二叉树按照二叉链表形式存储。
解题代码
ListNode* linkingLeaves(TreeNode* root) {queue<TreeNode*> q;q.emplace(root);ListNode* dummy = new ListNode(-1);ListNode* curNode = dummy;while (!q.empty()) {TreeNode* fNode = q.front();q.pop();if (fNode->left == nullptr && fNode->right == nullptr) {curNode->next = new ListNode(fNode->val);curNode = curNode->next;}if (fNode->left != nullptr) {q.emplace(fNode->left);}if (fNode->right != nullptr) {q.emplace(fNode->right);}}return dummy->next;
}
相似二叉树
题目描述
试设计判断两棵二叉树是否相似的算法。所谓二叉树 T1 和 T2 相似,指的是 T1 和 T2 都是空的二叉树或都只有一个根节点;或者 T1 的左子树和 T2 的左子树是相似的,且 T1 的右子树和 T2 的右子树是相似的。
解题代码
bool similarBT(TreeNode* root1, TreeNode * root2) {if (root1 == nullptr && root2 == nullptr) return true;if ((root1 == nullptr) ^ (root2 == nullptr)) return false;if (root1->left == nullptr && root1->right == nullptr && root2->left == nullptr && root2->right == nullptr) {return true;}return similarBT(root1->left, root2->left) && similarBT(root1->right, root2->right);
}
二叉树的带权路径长度和
题目描述
二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和,给定一棵二叉树,其叶结点的 val 域保存该结点的非负权值。设 root 为指向 T 的根节点的指针,设计求 T 的 WPL 的算法。
解题代码
BFS
int getWPL(TreeNode* root) {queue<TreeNode*> q, nq;q.emplace(root);int res = 0;for (int len = 0; !q.empty(); ++len) {while (!q.empty()) {TreeNode* fNode = q.front();q.pop();if (fNode->left == nullptr && fNode->right == nullptr) {res += fNode->val * len;}if (fNode->left != nullptr) {nq.emplace(fNode->left);}if (fNode->right != nullptr) {nq.emplace(fNode->right);}}q = move(nq);}return res;
}
DFS
int dfs(TreeNode* root, int depth) {if (root == nullptr) return 0;if (root->left == nullptr && root->right == nullptr) {return root->val * depth;}return dfs(root->left, depth + 1) + dfs(root->right, depth + 1);
}int getWPL(TreeNode* root) {return dfs(root, 0);
}
表达式树转表达式
题目描述
请设计一个算法,将给定表达式树转换为对应的中缀表达式并输出。
解题代码
void dfs(TreeNode<char>* root, int depth) {if (root == nullptr) return;if (root->left == nullptr && root->right == nullptr) {cout << root->val;}else {if (depth > 1) cout << "(";dfs(root->left, depth + 1);cout << root->val;dfs(root->right, depth + 1);if (depth > 1) cout << ")";}
}void getInfixExp(TreeNode<char>* root) {dfs(root, 1);
}
判定顺序存储二叉树是否为二叉搜索树
题目描述
已知非空二叉树 T 结点值均为正整数,采用顺序存储方式存储,T 中不存在的结点在数组中用 -1 表示。请设计一个尽可能高效的算法,判定一棵采用这种方式存储的二叉树是否为二叉搜索树。
解题代码
bool dfs(vector<int>& T, int idx, int& lastVal) {if (idx - 1 >= T.size() || T[idx - 1] == -1) return true;if (!dfs(T, idx * 2, lastVal) || T[idx - 1] <= lastVal) return false;lastVal = T[idx - 1];return dfs(T, idx * 2 + 1, lastVal);
}bool isBST(vector<int>& T) {int lastVal = INT32_MIN;return dfs(T, 1, lastVal);
}
根据层序序列建立二叉树
题目描述
设一棵二叉树层序遍历序列存储于一个一维数组中,空结点用 INT32_MAX 表示,试编写算法建立该二叉树的二叉链表。
解题代码
TreeNode* createTreeByOrder(vector<int>& order) {if (order.front() == INT32_MAX) return nullptr;queue<TreeNode*> q;int idx = 0;TreeNode* root = new TreeNode(order[idx++]);q.emplace(root);while (!q.empty()) {TreeNode* fNode = q.front();q.pop();if (fNode == nullptr) continue;if (idx < order.size()) {TreeNode* lChild = nullptr;if (order[idx] != INT32_MAX) {lChild = new TreeNode(order[idx]);}fNode->left = lChild;q.emplace(lChild);++idx;}if (idx < order.size()) {TreeNode* rChild = nullptr;if (order[idx] != INT32_MAX) {rChild = new TreeNode(order[idx]);}fNode->right = rChild;q.emplace(rChild);++idx;}}return root;
}
相关文章:

王道数据结构编程题 二叉树
二叉树定义 以下为本文解题代码的二叉树定义。 struct TreeNode {int val;TreeNode* left, *right;TreeNode(int val 0, TreeNode* left nullptr, TreeNode* right nullptr): val(val), left(left), right(right) {} };非递归后序遍历 题目描述 编写后序遍历二叉树的非递…...

登录怎么实现的,密码加密了嘛?使用明文还是暗文,知道怎么加密嘛?
在Java中登录功能的实现通常包括以下步骤,其中密码应该以加密形式存储在数据库中,而不以明文形式存储,以增强安全性: 登录功能的实现步骤: 用户输入: 用户在登录页面上输入用户名和密码。 传输到服务器&a…...

Nginx和Tomcat负载均衡实现session共享
以前的项目使用Nginx作为反向代理实现了多个Tomcat的负载均衡,为了实现多个Tomcat之间的session共享,使用了开源的Memcached-Session-Manager框架。 此框架的优势: 1、支持Tomcat6和Tomcat7 2、操作粘性或不黏性Session 3、没有单点故障 4、T…...

【算法题】210. 课程表 II
题目: 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。 例如,想要学习课程 0 ,…...

“数据类型不一致”会走索引吗?
分析&回答 字符串类型的索引 id_1 varchar(20) NOT NULL这样下面两条语句的结果是一样的: SELECT * FROM ix_test WHERE id_11; SELECT * FROM ix_test WHERE id_11;执行计划是不同的: mysql> explain select * from ix_test where id_11; | 1 …...

Leetcode 1572.矩阵对角线元素之和
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例 1: 输入:mat [[1,2,3],[4,5,6],[7,8,9]] 输出:25 解释:对角线的和为ÿ…...
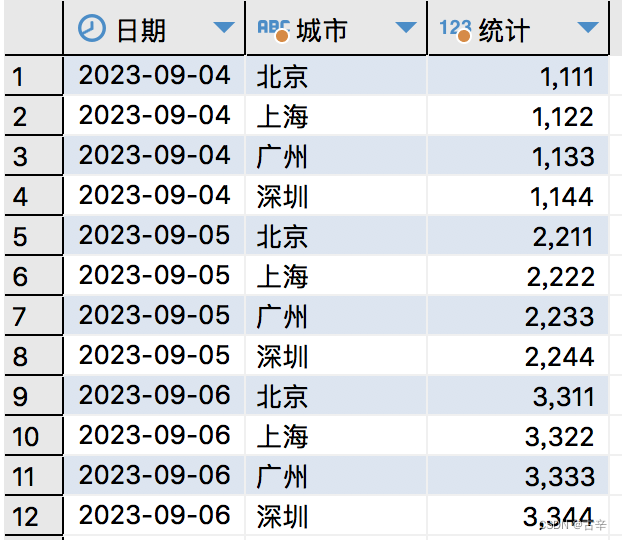
[PG]将一行数据打散成多行数据
原始数据 比如有如此表结构定义: 假如查询数据如下: select dt as "日期",bj_count as "北京", sh_count as "上海",gz_count as "广州", sz_count as "深圳" from city_stats order by dt--------------------…...

二蛋赠书一期:《快捷学习Spring》
文章目录 前言活动规则参与方式本期赠书《快捷学习Spring》关于本书作者介绍内容简介读者对象 结语 前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,…...
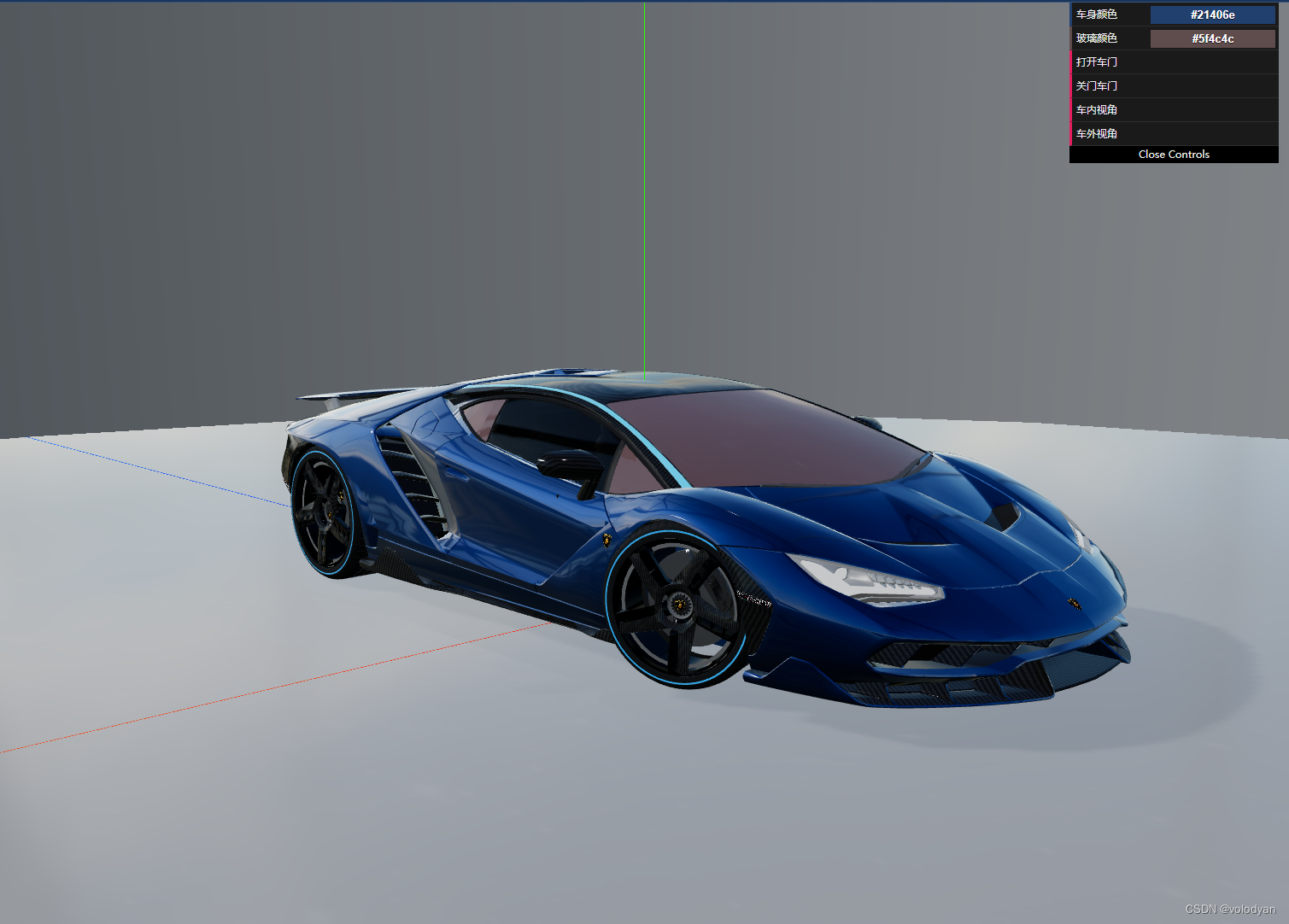
Threejs汽车展厅
2023-09-06-16-29-40 预览:https://9kt8fy-1234.csb.app/ 源码链接...
)
LeetCode:207. 课程表、210. 课程表 II(拓扑排序 C++)
目录 207. 课程表 题目描述: 实现代码与解析: 拓扑排序 210. 课程表 II 题目描述: 实现代码与解析: 拓扑排序 原理思路: 207. 课程表 题目描述: 你这个学期必须选修 numCourses 门课程࿰…...

如何使用组件
可以复用的代码写到组件里面,比如左侧的导航栏 1.写好一个组件 记得结构写在template标签里面,当然div也可以 2.在需要使用的地方,用标签使用组件 3.在使用的文件内import此组件 import CommonAside from /components/CommonAside.vue; …...
)
Android 13.0 Launcher3定制之双层改单层(去掉抽屉式二)
1.概述 在13.0的系统产品开发中,对于在Launcher3中的抽屉模式也就是双层模式,在系统原生的Launcher3中就是双层抽屉模式的, 但是在通过抽屉上滑的模式拉出app列表页,但是在一些产品开发中,对于单层模式的Launcher3的产品模式也是常用的功能, 所以需要了解抽屉模式,然后修…...
对卷积的一点具象化理解
前言 卷积的公式一般被表示为下式: 对新手来说完全看不懂这是干什么,这个问题需要结合卷积的应用场景来说。 原理 卷积比较广泛的应用是在信号与系统中,所以有些公式的定义会按照信息流的习惯。假设存在一串信号g(x)经过一个响应h(x)时他的响…...

NV12数据格式转H265编码格式实现过程
一、需求 在视频处理和传输应用中,将视频数据编码为高效的格式是非常重要的。H.265(也称为HEVC)是一种先进的视频编码标准,具有更好的压缩性能和图像质量,相比于传统的编码标准(如H.264)&#…...

ubuntu 22.04 深度学习环境配置
第一步 安装驱动 网址:https://www.nvidia.com/download/index.aspx 根据硬件选择,我这里是 ubuntu 服务器,显卡是v100 sudo su root chmod ax NVIDIA //按 TAB 即可 加运行权限 # 禁用原显卡驱动 vim /etc/modprobe.d/blacklist.conf # 在最后一行…...

支付宝小程序集成mqtt兼容IOS和安卓
1. 前言 去年就想做支付宝小程序接入mqtt协议。但最终多方咨询,问客服问社区得到的答案都是支付宝小程序不能直接支持mqtt协议。偶然间发现徐宏大神的佳作,终于发现了xmqtt.js这个好东西。它实现了支付宝小程序完美接入mqtt协议,设备可以…...
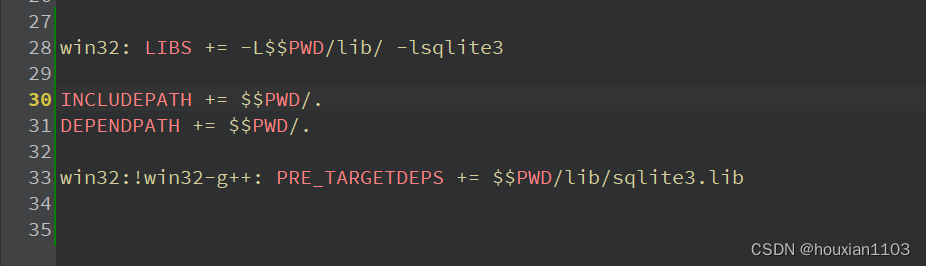
在Qt5中SQLite3的使用
一、SQLite简要介绍 什么是SQLite SQLite是一个进程内的库,实现了自给自足的、无服务器的、零配置的、事务性的 SQL 数据库引擎。它是一个零配置的数据库,这意味着与其他数据库不一样,您不需要在系统中配置。 就像其他数据库,S…...

使用Docker部署debezium来监控 MySQL 数据库
使用Docker部署debezium来监控 MySQL 数据库 Debezium是一个分布式平台,它将来自现有数据库的信息转换为事件流,使应用程序能够检测并立即响应数据库中的行级更改。 Debezium构建在Apache Kafka之上,并提供了一组Kafka Connect兼容的连接器。每个连接器都与特定的数据库管…...

百度低质量站点怎么办?解决百度低质量站点的方法和工具
百度低质量站点怎么恢复?这是许多网站主和运营人员在SEO优化过程中经常面临的一个问题。百度作为中国最大的搜索引擎,对于网站收录和排名具有至关重要的影响。然而,由于各种原因,有些网站可能面临被百度降权或收录减少的情况。那么…...

MSOS604A是德科技keysight MSOS604A示波器
181/2461/8938Infiniium S系列示波器融合了创新技术,旨在提供卓越的测量。新的10位ADC和低噪声前端技术协同工作,提供高达8 GHz的性能和业界最佳的信号完整性。一个高级框架,配有可快速启动的固态硬盘、可轻松触摸的15英寸电容式显示屏和可快…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
