Leetcode 1572.矩阵对角线元素之和

给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
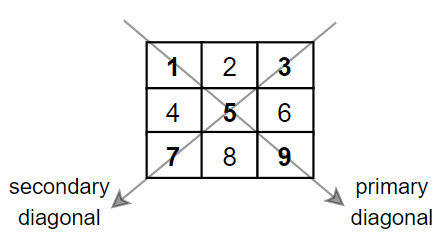
输入:mat = [[1,2,3],[4,5,6],[7,8,9]] 输出:25 解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25 请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1],[1,1,1,1],[1,1,1,1],[1,1,1,1]] 输出:8
示例 3:
输入:mat = [[5]] 输出:5
提示:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
通过次数
63.3K
提交次数
75.9K
通过率
83.3%
一、信息
1.给一个正方型矩阵mat
2.返回矩阵对角线元素的和
二、分析
条件1和条件2:告诉我此次的目的
问题1:该如何求和呢
根据我的思考步骤
第一步 观察在矩阵中对角线元素的下标特征
通过观察我发现主对角线上数组元素的下标都满足i=j
副对角线都满足(n-1,0)(0,n-1)即关于主对角线对称,我觉得我该回去修一下线性代数了。
第二步 我们通过for循环实现累加,if选择语句结构来筛选。
问题出现1:对了题目并没有说矩阵是几×几的矩阵所以还得测算矩阵的大小
问题出现该如何测算矩阵的大小
已知测算矩阵长度的是length函数。
答案:
Leetcode答案:
int n = mat.size(), sum = 0;问题出现2:根据题目我们不难发现不仅我们要计算该二维数组的大小还要开辟动态的空间,这在C++该怎么办呢?
很简答其实用vector即可,如果不记得可以看文章(知识不足的地方)
不知道陷入了停滞
我的答案:
我的答案:
首先我们可以分析这个问题如下:
1. **思考过程**:
- 我们需要计算主对角线和副对角线上的元素和。主对角线上的元素位置是`mat[i][i]`,副对角线上的元素位置是`mat[i][n-1-i]`。
- 如果矩阵的尺寸是奇数,则中心元素会被计算两次,我们需要减去一次。
2. **分析过程**:
- 我们可以通过一个循环从 0 到 n-1 来遍历所有的行(或列),然后计算对角线元素的和。
- 如果 n 是奇数,我们减去一次`mat[n/2][n/2]`。
现在我们可以将这个逻辑实现为 C、C++ 和 Java 程序:
### C 语言实现
#include <stdio.h>int diagonalSum(int** mat, int matSize, int* matColSize){int sum = 0;for(int i = 0; i < matSize; i++){sum += mat[i][i] + mat[i][matSize - 1 - i];}if(matSize % 2 == 1){sum -= mat[matSize / 2][matSize / 2];}return sum;
}int main() {int mat1[3][3] = {{1,2,3}, {4,5,6}, {7,8,9}};int* mat1_ptr[3] = {mat1[0], mat1[1], mat1[2]};printf("%d\n", diagonalSum(mat1_ptr, 3, NULL)); // Output: 25return 0;
}### C++ 语言实现
#include <vector>
#include <iostream>int diagonalSum(std::vector<std::vector<int>>& mat) {int sum = 0;int n = mat.size();for(int i = 0; i < n; i++) {sum += mat[i][i] + mat[i][n - 1 - i];}if(n % 2 == 1) {sum -= mat[n / 2][n / 2];}return sum;
}int main() {std::vector<std::vector<int>> mat1 = {{1,2,3}, {4,5,6}, {7,8,9}};std::cout << diagonalSum(mat1) << std::endl; // Output: 25return 0;
}### Java 语言实现
public class Main {public static int diagonalSum(int[][] mat) {int sum = 0;int n = mat.length;for(int i = 0; i < n; i++) {sum += mat[i][i] + mat[i][n - 1 - i];}if(n % 2 == 1) {sum -= mat[n / 2][n / 2];}return sum;}public static void main(String[] args) {int[][] mat1 = {{1,2,3}, {4,5,6}, {7,8,9}};System.out.println(diagonalSum(mat1)); // Output: 25}
}每种语言的实现都遵循了我们的原始分析和设计,结合了相应语言的特性和语法来实现目标功能。
Leetcode题解:
方法一:遍历矩阵
思路与算法
我们知道矩阵中某个位置 (i,j)(i,j)(i,j) 处于对角线上,则一定满足下列条件之一:
i=ji = ji=j;
i+j=n−1i + j = n - 1i+j=n−1;
根据上述结论,我们可以遍历整个矩阵,如果当前坐标 (i,j)(i, j)(i,j) 满足 i=ji = ji=j 或者 i+j=n−1i + j = n - 1i+j=n−1 则表示该位置一定在对角线上,则把当前的数字加入到答案之中。
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;}
};C:
int diagonalSum(int** mat, int matSize, int* matColSize) {int n = matSize, sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;
}JAVA:
class Solution {public int diagonalSum(int[][] mat) {int n = mat.length, sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;}
}
方法二:枚举对角线元素
思路与算法
逐行遍历,记当前的行号为 iii,则当前行中处于对角线的元素为: 坐标 (i,i)(i, i)(i,i) 和坐标 (i,n−i−1)(i, n - i - 1)(i,n−i−1),因此我们把 (i,i)(i, i)(i,i) 与 (i,n−i−1)(i, n - i - 1)(i,n−i−1) 处的数字加入到答案中。 如果 nnn 是奇数的话,则主对角线与副对角线存在交点 (⌊n2⌋,⌊n2⌋)(\lfloor \dfrac{n}{2} \rfloor,\lfloor \dfrac{n}{2} \rfloor)(⌊
2
n
⌋,⌊
2
n
⌋),该点会被计算两次。所以当 nnn 为奇数的时候,需要减掉交点处的值。
C++:
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0, mid = n / 2;for (int i = 0; i < n; ++i) {sum += mat[i][i] + mat[i][n - 1 - i];}return sum - mat[mid][mid] * (n & 1);}
};总结:
从这道题目中,我们可以学到以下几点:
1. **数组索引的应用**:该题目教会我们如何利用数组索引来找到主对角线和副对角线的元素。这对于深入理解数组索引和二维数组非常有帮助。
2. **循环的优化**:我们可以通过仔细设计循环来减少不必要的计算。例如,方法二比方法一更优,因为它避免了遍历整个数组,而是只关注于对角线元素。
3. **条件运算符的使用**:该题目展示了如何使用条件运算符(如`&`用于检测奇偶性)来简化代码和减少计算。
4. **复杂度分析**:通过比较两种方法,我们可以学习到如何通过减少循环次数和减少重复计算来降低算法的时间复杂度。
5. **编程语言的特性**:通过用多种编程语言(C, C++ 和 Java)来解这个问题,我们可以学习和比较不同语言中数组和循环结构的不同实现和语法。
6. **数学应用在编程中**:这个问题也是一个很好的例子,展示了数学(特别是线性代数)在编程和算法设计中的应用。
7. **代码测试与调试**:实现代码后,我们可以创建多种测试用例来验证代码的正确性和效率,从而提高我们的测试和调试技能。
8. **问题解决技能的培养**:整体来说,解决这种问题可以帮助我们培养分析问题和找到有效解决方案的技能。

相关文章:

Leetcode 1572.矩阵对角线元素之和
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例 1: 输入:mat [[1,2,3],[4,5,6],[7,8,9]] 输出:25 解释:对角线的和为ÿ…...
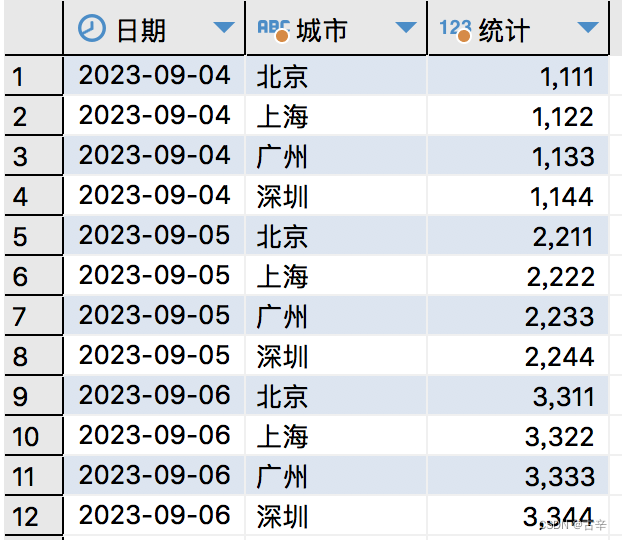
[PG]将一行数据打散成多行数据
原始数据 比如有如此表结构定义: 假如查询数据如下: select dt as "日期",bj_count as "北京", sh_count as "上海",gz_count as "广州", sz_count as "深圳" from city_stats order by dt--------------------…...

二蛋赠书一期:《快捷学习Spring》
文章目录 前言活动规则参与方式本期赠书《快捷学习Spring》关于本书作者介绍内容简介读者对象 结语 前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,…...
Threejs汽车展厅
2023-09-06-16-29-40 预览:https://9kt8fy-1234.csb.app/ 源码链接...
)
LeetCode:207. 课程表、210. 课程表 II(拓扑排序 C++)
目录 207. 课程表 题目描述: 实现代码与解析: 拓扑排序 210. 课程表 II 题目描述: 实现代码与解析: 拓扑排序 原理思路: 207. 课程表 题目描述: 你这个学期必须选修 numCourses 门课程࿰…...

如何使用组件
可以复用的代码写到组件里面,比如左侧的导航栏 1.写好一个组件 记得结构写在template标签里面,当然div也可以 2.在需要使用的地方,用标签使用组件 3.在使用的文件内import此组件 import CommonAside from /components/CommonAside.vue; …...
)
Android 13.0 Launcher3定制之双层改单层(去掉抽屉式二)
1.概述 在13.0的系统产品开发中,对于在Launcher3中的抽屉模式也就是双层模式,在系统原生的Launcher3中就是双层抽屉模式的, 但是在通过抽屉上滑的模式拉出app列表页,但是在一些产品开发中,对于单层模式的Launcher3的产品模式也是常用的功能, 所以需要了解抽屉模式,然后修…...
对卷积的一点具象化理解
前言 卷积的公式一般被表示为下式: 对新手来说完全看不懂这是干什么,这个问题需要结合卷积的应用场景来说。 原理 卷积比较广泛的应用是在信号与系统中,所以有些公式的定义会按照信息流的习惯。假设存在一串信号g(x)经过一个响应h(x)时他的响…...

NV12数据格式转H265编码格式实现过程
一、需求 在视频处理和传输应用中,将视频数据编码为高效的格式是非常重要的。H.265(也称为HEVC)是一种先进的视频编码标准,具有更好的压缩性能和图像质量,相比于传统的编码标准(如H.264)&#…...

ubuntu 22.04 深度学习环境配置
第一步 安装驱动 网址:https://www.nvidia.com/download/index.aspx 根据硬件选择,我这里是 ubuntu 服务器,显卡是v100 sudo su root chmod ax NVIDIA //按 TAB 即可 加运行权限 # 禁用原显卡驱动 vim /etc/modprobe.d/blacklist.conf # 在最后一行…...

支付宝小程序集成mqtt兼容IOS和安卓
1. 前言 去年就想做支付宝小程序接入mqtt协议。但最终多方咨询,问客服问社区得到的答案都是支付宝小程序不能直接支持mqtt协议。偶然间发现徐宏大神的佳作,终于发现了xmqtt.js这个好东西。它实现了支付宝小程序完美接入mqtt协议,设备可以…...
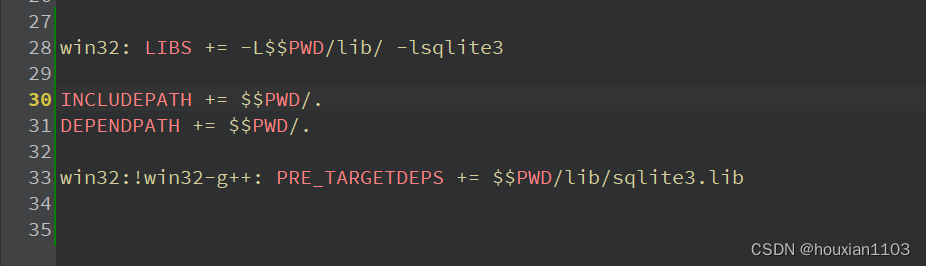
在Qt5中SQLite3的使用
一、SQLite简要介绍 什么是SQLite SQLite是一个进程内的库,实现了自给自足的、无服务器的、零配置的、事务性的 SQL 数据库引擎。它是一个零配置的数据库,这意味着与其他数据库不一样,您不需要在系统中配置。 就像其他数据库,S…...

使用Docker部署debezium来监控 MySQL 数据库
使用Docker部署debezium来监控 MySQL 数据库 Debezium是一个分布式平台,它将来自现有数据库的信息转换为事件流,使应用程序能够检测并立即响应数据库中的行级更改。 Debezium构建在Apache Kafka之上,并提供了一组Kafka Connect兼容的连接器。每个连接器都与特定的数据库管…...

百度低质量站点怎么办?解决百度低质量站点的方法和工具
百度低质量站点怎么恢复?这是许多网站主和运营人员在SEO优化过程中经常面临的一个问题。百度作为中国最大的搜索引擎,对于网站收录和排名具有至关重要的影响。然而,由于各种原因,有些网站可能面临被百度降权或收录减少的情况。那么…...

MSOS604A是德科技keysight MSOS604A示波器
181/2461/8938Infiniium S系列示波器融合了创新技术,旨在提供卓越的测量。新的10位ADC和低噪声前端技术协同工作,提供高达8 GHz的性能和业界最佳的信号完整性。一个高级框架,配有可快速启动的固态硬盘、可轻松触摸的15英寸电容式显示屏和可快…...
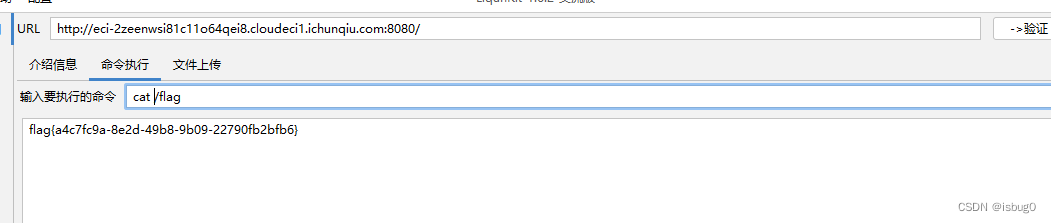
春秋云镜 CVE-2016-0785
春秋云镜 CVE-2016-0785 S2-029 靶标介绍 2.3.28 之前的 Apache Struts 2.x 允许远程攻击者通过标签属性中的“%{}”序列执行任意代码。 启动场景 漏洞利用 工具利用 得到flag flag{a4c7fc9a-8e2d-49b8-9b09-22790fb2bfb6}...

入门ElasticSearch :为什么选择ES作为搜索引擎?
介绍 随着数据量的不断增长,搜索和分析大规模数据集变得越来越重要。传统数据库在面对这种需求时往往表现不佳,这时候就需要一种专门用于搜索和分析的引擎。ElasticSearch (简称ES)就是这样一款强大的搜索引擎,它具有许…...

汽车安全及标准
汽车安全及标准 我们的测试系统如何处理整个标准? 您是否需要处理汽车行业的一系列标准? 不同的标准侧重于驱动逆变器的安全性和功能性: 功能安全(ISO 26262)信号和低压车载网络(LV 124、LV 148 和 VDA …...
APP备案流程详细解读
背景介绍 2023年8月4日,工信部发布《工业和信息化部关于开展移动互联网应用程序备案工作的通知》。 在中华人民共和国境内从事互联网信息服务的APP主办者,应当依照《中华人民共和国反电信网络诈骗法》《互联网信息服务管理办法》(国务院令第…...
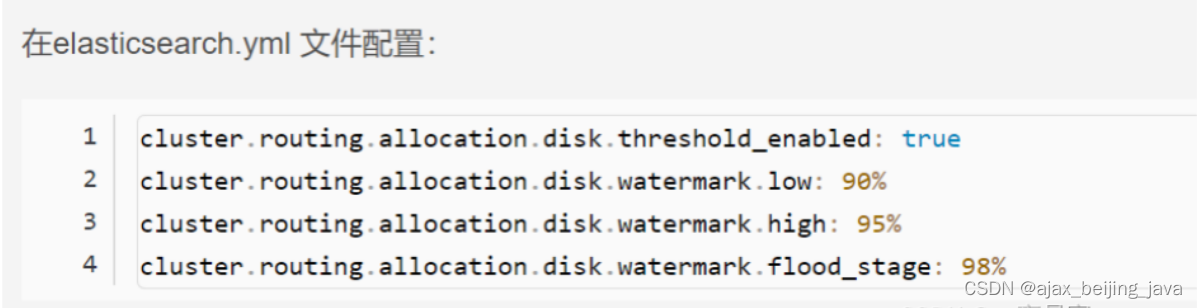
ES 集群常用排查命令
说明:集群使用非默认端口9200,使用的是7116端口举例 一、常用命令 #1.集群健康状态 [wlsadminelastic-01~]$ curl -XGET "http://10.219.27.00:7116/_cluster/health?pretty" { cluster name":"cluster" "status"…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
