OpenCV(三十四):轮廓外接最大、最小矩形和多边形拟合
目录
1.轮廓外接最大矩形boundingRect()
2.轮廓外接最小矩形minAreaRect()
3.轮廓外接多边形approxPolyDP()
1.轮廓外接最大矩形boundingRect()
Rect cv::boundingRect ( InputArray array )
- array:输入的灰度图像或者2D点集,数据类型为vector<Point>或者Mat。
示例代码:
//轮廓最大外接矩阵
void Contour_external_maxmatrix(Mat image) {Mat gray,binary;cvtColor(image,gray,COLOR_BGR2GRAY);//灰度化GaussianBlur(gray,gray,Size(9,9),2,2);//滤波threshold(gray,binary,170,255,THRESH_BINARY|THRESH_OTSU);//自适应二值化//轮廓检测vector<vector<Point>> contours;//轮廓vector<Vec4i> hierarchy;//存放轮廓结构变量findContours(binary,contours,hierarchy,RETR_TREE,CHAIN_APPROX_SIMPLE,Point());//寻找轮廓的外接矩阵for(int n=0;n<contours.size();n++) {//最大外接矩阵Rect rect = boundingRect(contours[n]);rectangle(image, rect, Scalar(7, 67, 255), 2, 8, 0);}imwrite("/sdcard/DCIM/max.png",image);
}轮廓外接最大矩形的结果:

2.轮廓外接最小矩形minAreaRect()
RotatedRect cv::minAreaRect ( InputArray points )
- array:输入的灰度图像或者2D点集,数据类型为vector<Point>或者Mat。
示例代码:
//轮廓最小外接矩阵
void Contour_external_minmatrix(Mat image){Mat gray,binary;cvtColor(image,gray,COLOR_BGR2GRAY);//灰度化GaussianBlur(gray,gray,Size(9,9),2,2);//滤波threshold(gray,binary,170,255,THRESH_BINARY|THRESH_OTSU);//自适应二值化//轮廓检测vector<vector<Point>> contours;//轮廓vector<Vec4i> hierarchy;//存放轮廓结构变量findContours(binary,contours,hierarchy,RETR_TREE,CHAIN_APPROX_SIMPLE,Point());//寻找轮廓的外接矩阵for(int n=0;n<contours.size();n++) {//最小外接矩阵RotatedRect rrect= minAreaRect(contours[n]);Point2f points[4];rrect.points(points);//读取最小外接矩阵的四个顶点Point2f cpt=rrect.center;//最小外接矩阵的中心//绘制旋转矩阵与中心位置for(int i=0;i<4;i++){if(i==3){line(image,points[i],points[0],Scalar(0,0,255,255),2,8,0);break;}line(image,points[i],points[i+1],Scalar(0,0,255,255),2,8,0);}//绘制矩阵中心circle(image,cpt,4,Scalar(0,0,255,255),-1,8,0);}imwrite("/sdcard/DCIM/min.png",image);}
轮廓外接最小矩形的结果:

3.轮廓外接多边形approxPolyDP()
void cv::approxPolyDP (InputArray curve,
OutputArray approxCurve,
double epsilon,
bool closed
)
- curve:输入轮廓像素点。
- approxCurve:多边形逼近结果,以多边形顶点坐标的形式给出
- epsilon:逼近的精度,即原始曲线和逼近曲线之间的最大距离。
- closed:逼近曲线是否为封闭曲线的标志, true表示曲线封闭,即最后一个顶点与第一个顶点相连
示例代码:
void drawapp(Mat result,Mat img2){for(int i=0;i<result.rows;i++){//最后一个坐标点与第一个坐标点连接if(i==result.rows-1){Vec2i point1=result.at<Vec2i>(i);Vec2i point2=result.at<Vec2i>(0);line(img2,point1,point2,Scalar(0,0,255,255),4,8,0);break;}Vec2i point1=result.at<Vec2i>(i);Vec2i point2=result.at<Vec2i>(i+1);line(img2,point1,point2,Scalar(0,0,255,255),4,8,0);}}//轮廓多边形拟合
void Contour_external_matrix(Mat image){Mat gray,binary;cvtColor(image,gray,COLOR_BGR2GRAY);//灰度化// GaussianBlur(gray,gray,Size(9,9),2,2);//滤波// threshold(gray,binary,170,255,THRESH_BINARY|THRESH_OTSU);//自适应二值化//轮廓的发现与绘制vector<vector<Point>> contours;//轮廓vector<Vec4i> hierarchy;//存放轮廓结构变量findContours(gray,contours,hierarchy,RETR_TREE,CHAIN_APPROX_SIMPLE,Point());//绘制多边形for(int n=0;n<contours.size();n++) {//用最小外接矩阵求取轮廓中心RotatedRect rrect= minAreaRect(contours[n]);Point2f center=rrect.center;//最小外接矩阵的中心circle(image,center,2,Scalar(0,0,255,255),2,8,0);Mat result;approxPolyDP(contours[n],result,4,true);//多边形拟合drawapp(result,image);}imwrite("/sdcard/DCIM/matrix.png",image);}多边形拟合的结果:

相关文章:

OpenCV(三十四):轮廓外接最大、最小矩形和多边形拟合
目录 1.轮廓外接最大矩形boundingRect() 2.轮廓外接最小矩形minAreaRect() 3.轮廓外接多边形approxPolyDP() 1.轮廓外接最大矩形boundingRect() Rect cv::boundingRect ( InputArray array ) array:输入的灰度图像或者2D点集,数据类型为vector<Point>或者M…...
Kafka3.0.0版本——消费者(offset的默认维护位置)
目录 一、offset的默认维护位置1.1、offset的默认维护位置概述1.2、offset的默认维护位置图解 二、消费者offset的案例 一、offset的默认维护位置 1.1、offset的默认维护位置概述 Kafka0.9版本之前,consumer默认将offset保存在Zookeeper中。从Kafka0.9版本开始&am…...
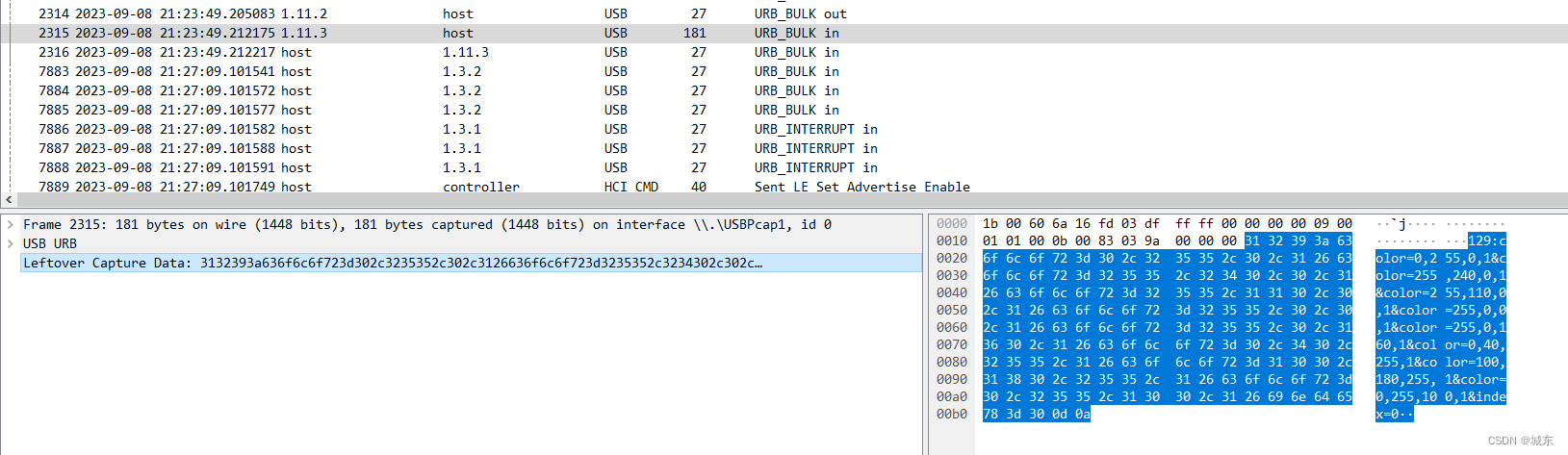
Wireshark技巧[监听串口包]
监听串口包 本文摘录于:https://blog.csdn.net/qq_20405005/article/details/79652927只是做学习备份之用,绝无抄袭之意,有疑惑请联系本人! 这里要保证安装了USBpcap: 打开USBpcap后一半都要输入过滤条件,否则USB太多数据了,比如…...

安全运营中心即服务提供商评估
如果组织当前没有自己的安全运营中心(SOC),那么可能需要考虑如何在不从头开始构建的情况下获得安全运营中心(SOC)。自己构建安全运营中心(SOC)的费用可能会非常昂贵,考虑到工作人员全天候运营的配置成本,就更是如此。在过去几年中,…...

算法通关村第十三关——幂运算问题解析
前言 幂运算为常见的数学运算,形式为 a b a^b ab ,其中a为底数,b为指数, 力扣中,幂运算相关的问题主要是判断一个数是不是特定正整数的整数次幂,以及快速幂的处理。 1.求2的幂 力扣231题,给…...

Python 之使用Numpy库来加载Numpy(.npy)文件并检查其内容
文章目录 总的介绍data.dtypedata.shapedata.ndimdata.size 总的介绍 要判断一个Numpy(.npy)文件的数据集类型,你可以使用Python中的Numpy库来加载该文件并检查其内容。以下是一些常见的步骤: 导入Numpy库: 首先&…...

C#学习系列之UDP同端口收发问题
C#学习系列之UDP同端口收发问题 前言解决办法关于JoinMulticastGroup总结 前言 想测试自己的程序问题,建立了两个UDP程序,一个往端口中接到数就传出去,另一个从这个端口接数据来解析。 出现的问题是 每次打开端口,另一个程序就无…...

SpringMVC之文件上传下载以及jrebel的使用
目录 一、文件上传 1.1 导入依赖 1.2 配置文件上传解析器 1.3 配置服务器存放文件地址 1.3.1 点击编辑Configurations 1.3.2 将项目部署至tomcat服务器上 1.3.3 配置相对路径 1.4 导入PropertiesUtil工具类 1.5 编写resource.properties 1.6 添加sql 1.7 编写PageCo…...

基于Fomantic UI Web构建 个人导航站点网站源码 网站技术导航源码
BYR-Navi-master好看有个性的网站技术导航源码 该网站基于Fomantic UI Web框架构建,整个项目的设计和构建具有高度的配置和定制灵活性。 整体风格比较适合个人导航站点使用 搜索框输入关键词后,点击上方搜索引擎图标可跳转打开对应搜索引擎搜索结果&am…...

DRF02-请求响应与路由
文章目录 1. http请求响应1.1. 请求与响应1.1.1 Request1.1.1.1 常用属性1).data2).query_params3)request._request基本使用1.1.2 Response1.1.2.1 构造方式1.1.2.2 response对象的属性1).data2).status_code3).content1.1.2.3 状态码1)信息告知 - 1xx2)成功 - 2xx3)…...

http直接调用paddlepaddle实现文字转语音,语音转文字
由于环境问题,折腾好久,记录下来,安装后使用还是很方便的 记录下来,方便自己,方便大家 1.安装 参考官方文档: mirrors / paddlepaddle / paddlespeech GitCode 2.启动server 参考官方文档: mirrors / paddlepaddle / paddlespeech GitCode 3.直接调用 参考官方文档: htt…...
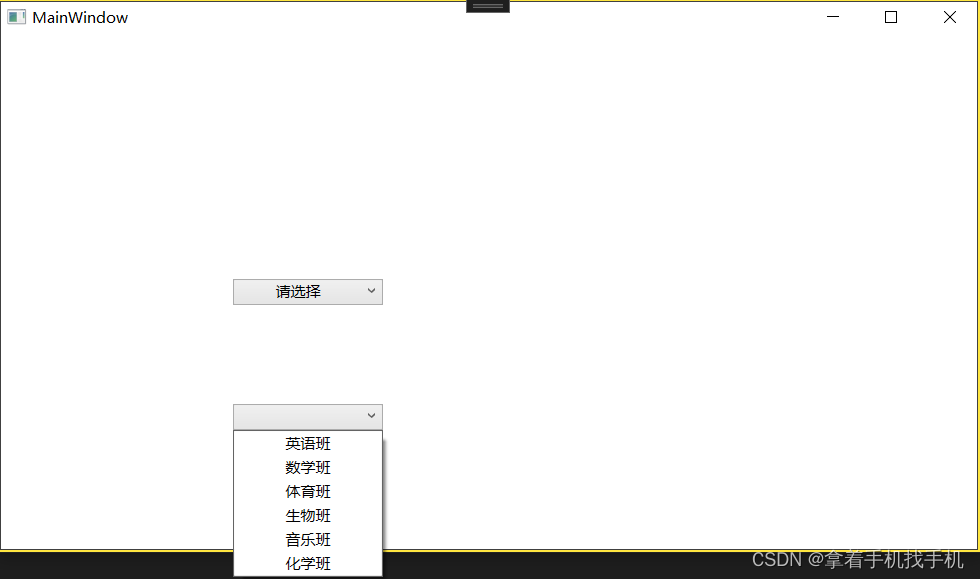
9. xaml ComboBox控件
1.运行图像 2.运行源码 a.Xaml源码 <Grid Name="Grid1"><!--IsDropDownOpen="True" 默认就是打开的--><ComboBox x:Name="co...
:密钥封装 KEM(附源码分析))
【后量子密码】CRYSTALS-KYBER 算法(二):密钥封装 KEM(附源码分析)
一、前言 Kyber 算法是一种满足 IND-CCA2 安全的密钥封装机制(key-encapsulation mechanism,KEM),其安全性依赖于MLWE 问题的困难性。Kyber 算法构建采用了两阶段的方法:首先引入了一种IND-CPA 安全的公钥加密方案,用于加密长度为32字节的消息,称之为Kyber.CPAPKE;然后…...

什么是原⼦操作?在 JUC 中有哪些原⼦类?
原子操作是一种在多线程环境下不会被中断的操作,它要么完全执行,要么完全不执行,不会出现中间状态。原子操作通常是对共享数据的操作,确保多个线程同时访问共享数据时不会导致数据不一致或损坏。 在Java中,java.util.concurrent 包提供了一组原子类,用于执行原子操作。以…...

2022年12月 C/C++(八级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:生理周期 人生来就有三个生理周期,分别为体力、感情和智力周期,它们的周期长度为23天、28天和33天。每一个周期中有一天是高峰。在高峰这天,人会在相应的方面表现出色。例如,智力周期的高峰,人会思维敏捷,精力容易高度集中。因…...

Hadoop的HDFS的集群安装部署
注意:主机名不要有/_等特殊的字符,不然后面会出问题。有问题可以看看第5点(问题)。 1、下载 1.1、去官网,点下载 下载地址:https://hadoop.apache.org/ 1.2、选择下载的版本 1.2.1、最新版 1.2.2、其…...
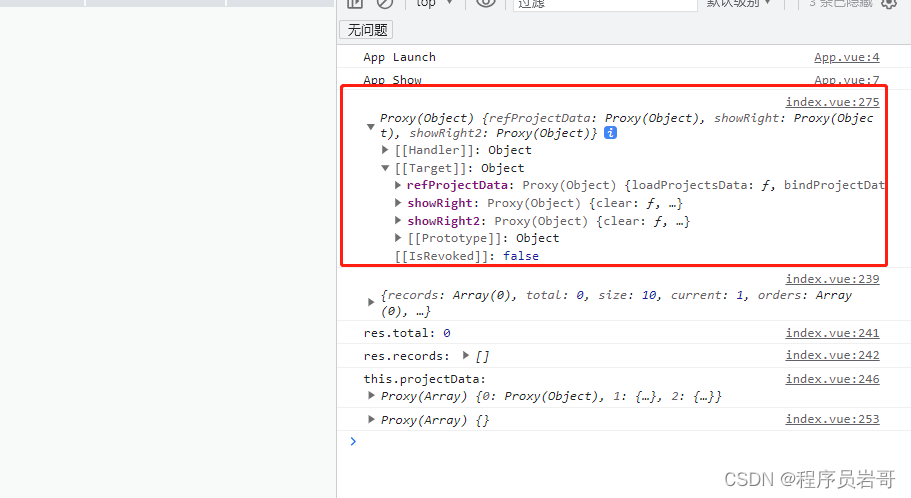
uniapp 在 onLoad 事件中 this.$refs 娶不到的问题
现象 本人想在主页面加载的时候调用子组件的方法。示例代码如下: 运行,发现 this.$refs 取不到。如下图所示: 解决方法,把onLoad 换为 onReady 就可以了。...

常見算法時間複雜度分析
当我们进行算法分析时,通常会忽略掉常数倍数的因子和低阶项,只考虑最高阶的项。这是因为在大规模问题下,较小的项和常数倍数的因子相对于最高阶的项来说变得可以忽略不计。 以下是一些常见的示例,说明了常数倍数的因子和高阶项对…...

自学Python05-学会Python中的函数定义
亲爱的同学们,今天我们将开始学习 Python 中的函数。函数就像一个魔法盒子,可以让我们在程序中执行一段代码,并且可以反复使用。这样,我们的程序就可以变得更加简洁和易于理解。现在,让我们一起来学习如何使用函数吧&a…...
)
设计模式-组合模式(Composite)
文章目录 前言一、组合模式的概念二、组合模式的优缺点1.优点2.缺点 三、组合模式的实现总结 前言 组合模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树状结构以表示“整体-部分”的层次结构。组合模式使得客户端可以统…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
