it监控系统可以电脑吗?有什么效果
IT业务监控已经成为公司不可或缺的一部分,以确保业务的正常运行,提高企业的竞争能力。本文将详细介绍IT业务监控的必要性、实施方法以及如何选择合适的监控工具。
IT业务监控的必要性
确保业务稳定运行
IT业务监控可以实时检测公司的工作流程,确保业务系统能够及时发现和解决问题,从而保证业务的稳定运行。提高运维效率
通过对IT业务的实时监控,运维人员可以快速查找难题,减少故障处理时间,提高运维效率。减低公司成本
高效率的IT业务监控可以帮助企业及时发现潜在的安全隐患和性能瓶颈,从而减低公司成本。提高企业竞争力
通过IT业务监控,企业可以更好地了解自己的工作流程和经营状况,进而制定更合理的发展战略,提高企业的竞争能力。
实施IT业务监控的方法
确定监督目标
公司应根据自己的项目需求和发展战略,明确监控目标,包括关键业务的运行状况、系统的易用性、安全性等。制定监督对策
根据监管目标,企业应制定适当的监管对策,包括监管内容、监管频率、报警门槛等。选择监控工具
市场上有很多专业的IT业务监控工具,企业应该根据自己的需求和预算选择合适的监控工具。在选择过程中,应注意工具的功能、便利性和可扩展性。实施监控计划
公司应根据制定的监督计划和所选的监督工具实施具体的监督计划。在实施过程中,应注意与现有系统的兼容性和集成性。不断优化监控方案
伴随着企业的发展和市场的变化,企业应逐步完善监控方案,确保企业能够始终满足企业的项目需求和发展规划。如何选择IT业务监控工具?
功能性要求:公司应选择有效的工具,如性能监控、日志分析、报警通知等,以满足自己的项目需求。
方便:企业应选择操作简便、使用方便的工具,以降低运维人员的学习成本。
可扩展性:企业应选择扩展性强的工具,以便在未来根据项目需要进行升级和扩展。
技术支持:公司应选择提供优秀技术支持的工具提供商,以确保在遇到问题时能及时处理。
成本效益:企业应充分考虑工具的价格、维修费用等因素,选择性价比较高的工具。
总之,IT业务监控对于保证项目稳定运行、提高运维效率、减低公司成本具有重要意义。企业应根据自身需求和具体情况,选择合适的监控工具和方法,确保企业信息化建设和运营更加智能化和高效化。
相关文章:

it监控系统可以电脑吗?有什么效果
IT业务监控已经成为公司不可或缺的一部分,以确保业务的正常运行,提高企业的竞争能力。本文将详细介绍IT业务监控的必要性、实施方法以及如何选择合适的监控工具。 IT业务监控的必要性 确保业务稳定运行 IT业务监控可以实时检测公司的工作流程&#x…...
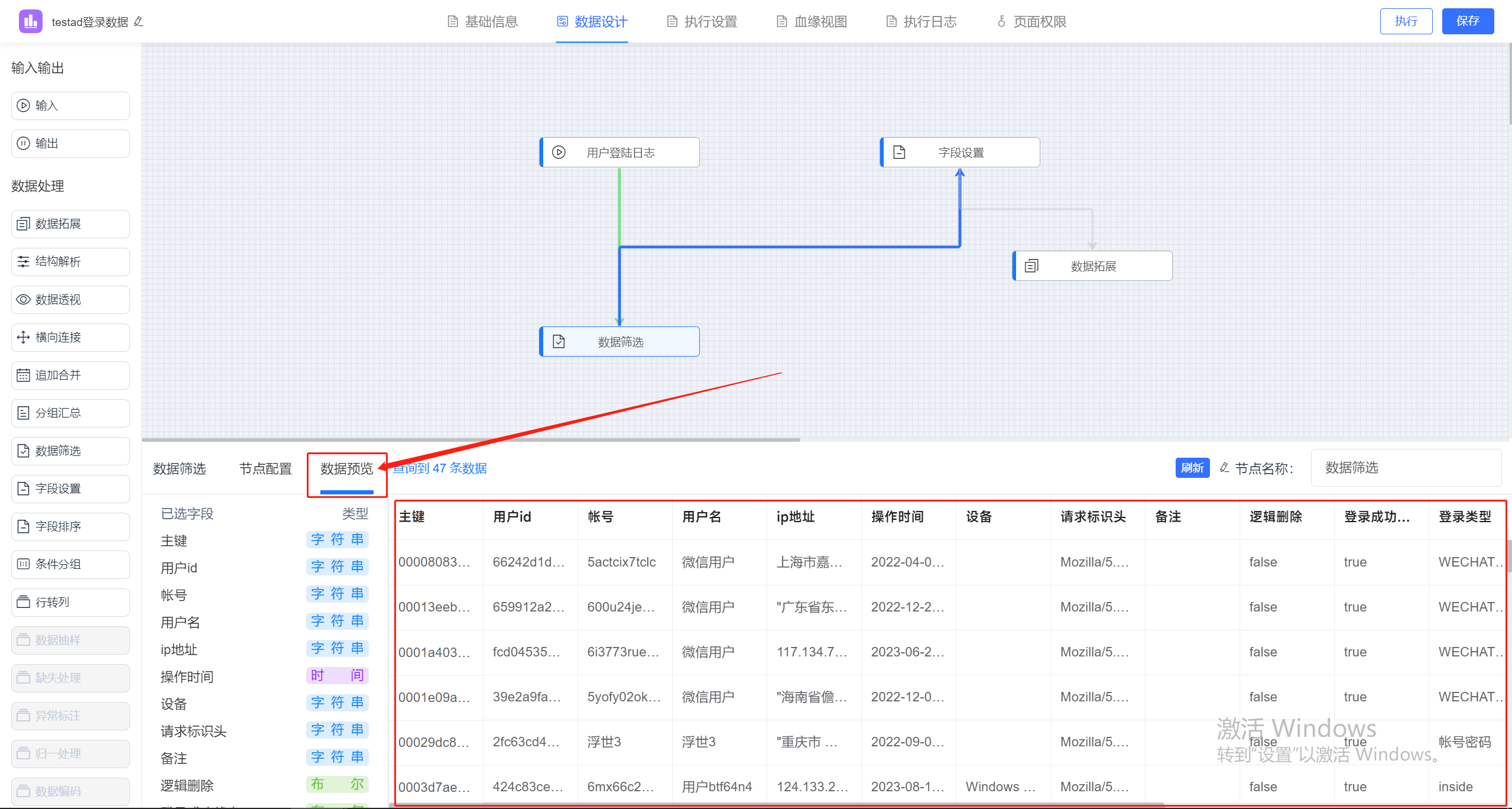
jvs-智能bi(自助式数据分析)9.1更新内容
jvs-智能bi更新功能 1.报表增加权限功能(服务、模板、数据集、数据源可进行后台权限分配) 每个报表可以独立设置权限,通过自定义分配,给不同的人员分配不同的权限。 2.报表新增执行模式 可选择首次报表加载数据为最新数据和历…...

MyBatis-Plus-扩展操作(3)
3.扩展 代码生成 逻辑删除 枚举处理器 json处理器 配置加密 分页插件 3.1 代码生成 https://blog.csdn.net/weixin_41957626/article/details/132651552 下载下面的插件 红色的是刚刚生成的。 我觉得不如官方的那个好用,唯一的好处就是勾选的选项能够看的懂得。…...

react 中 antd 的 样式和 tailwind 样式冲突
问题原因:在使用 tailwindcss 时,会导入大量的 tailwindcss 默认属性,而默认样式中 button, [typebutton] 包含了 background-color: transparent; 从而导致 antd Button 按钮背景色变成透明。解决办法:禁止 tailwindcss 的默认属…...
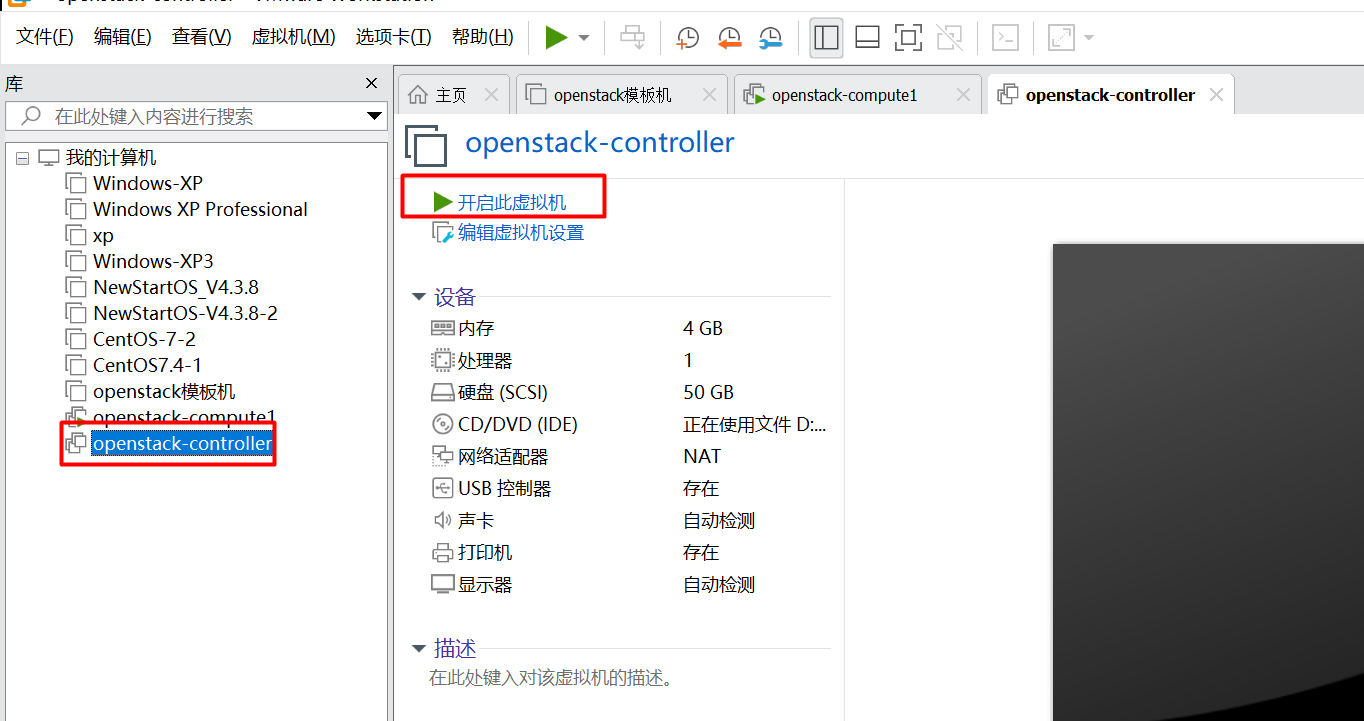
获取该虚拟机的所有权失败,主机上的某个应用程序正在使用该虚拟机
点击“openstack-controller”虚机 打开出现如下错误,点击“获取所有权” 点击“取消” 这时候不要删除虚拟机,这种错误一般是由于虚拟机没有正常关闭引起的。 找到openstack-controller的虚拟磁盘文件及配置文件存放的位置,删除openstack-…...

2024届校招-Java开发笔试题-S4卷
有三种题型:单项选择题(10道)、不定项选择题(10道)、编程题(3道) 下面是一些回忆的题目: 1.哪种设计模式将对象的创建与使用分离,通过工厂类创建对象 答:工…...
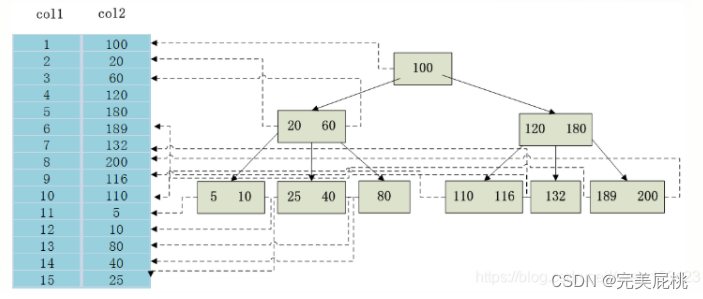
数据分析面试题(2023.09.08)
数据分析流程 总体分为四层:需求层、数据层、分析层和结论层 一、统计学问题 1、贝叶斯公式复述并解释应用场景 公式:P(A|B) P(B|A)*P(A) / P(B)应用场景:如搜索query纠错,设A为正确的词,B为输入的词,那…...

jenkins 报错fatal:could not read Username for ‘XXX‘:No such device or address
#原因:机器做迁移,或者断电,遇到突发情况 #解决: 一.排查HOME和USER环境变量 可以在项目执行shell脚本的时候echo $HOME和USER 也可以在构建记录位置点击compare environment 对比两次构建的环境变量 二.查看指定节点的git凭证 查…...
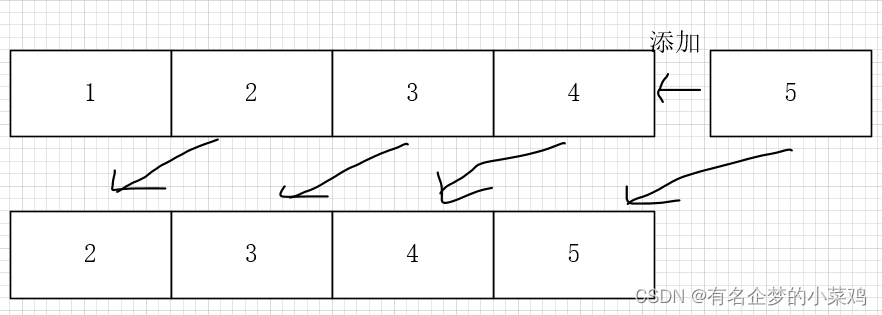
LRU算法之我见
文章目录 一、LRU算法是什么?二、使用原理三、代码实现总结 一、LRU算法是什么? LRU算法又称最近最少使用算法,它是是大部分操作系统为最大化页面命中率而广泛采用的一种页面置换算法。是一种缓存淘汰策略,根据使用频率来淘汰无用…...
)
【第20例】华为 IPD 体系 | IPD 的底层思考逻辑(限制版)
目录 简介 更新情况 IPD体系 CSDN学院 专栏目录 作者简介 简介 最近随着华为 Mate 60 系列的爆火发布。 这家差不多沉寂了 4 年的企业再次映入大众的眼帘。 其实,华为手机业务发展的元年最早可以追溯...
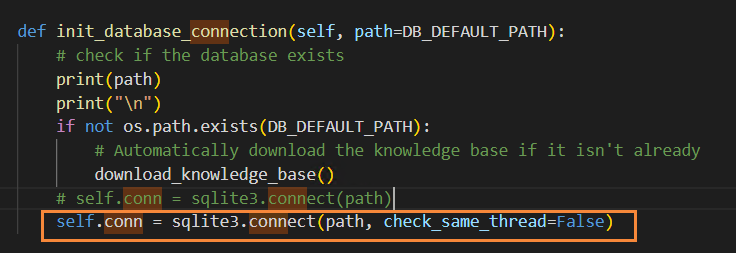
spaCy库的实体链接踩坑,以及spaCy-entity-linker的knowledge_base下载问题
问题1. spacy Can’t find factory for ‘entityLinker’ 1)问题 写了一个实体链接类,代码如下: nlp spacy.load("en_core_web_md")class entieyLink:def __init__(self, doc, nlp):self.nlp nlpself.doc self.nlp(doc)# Che…...
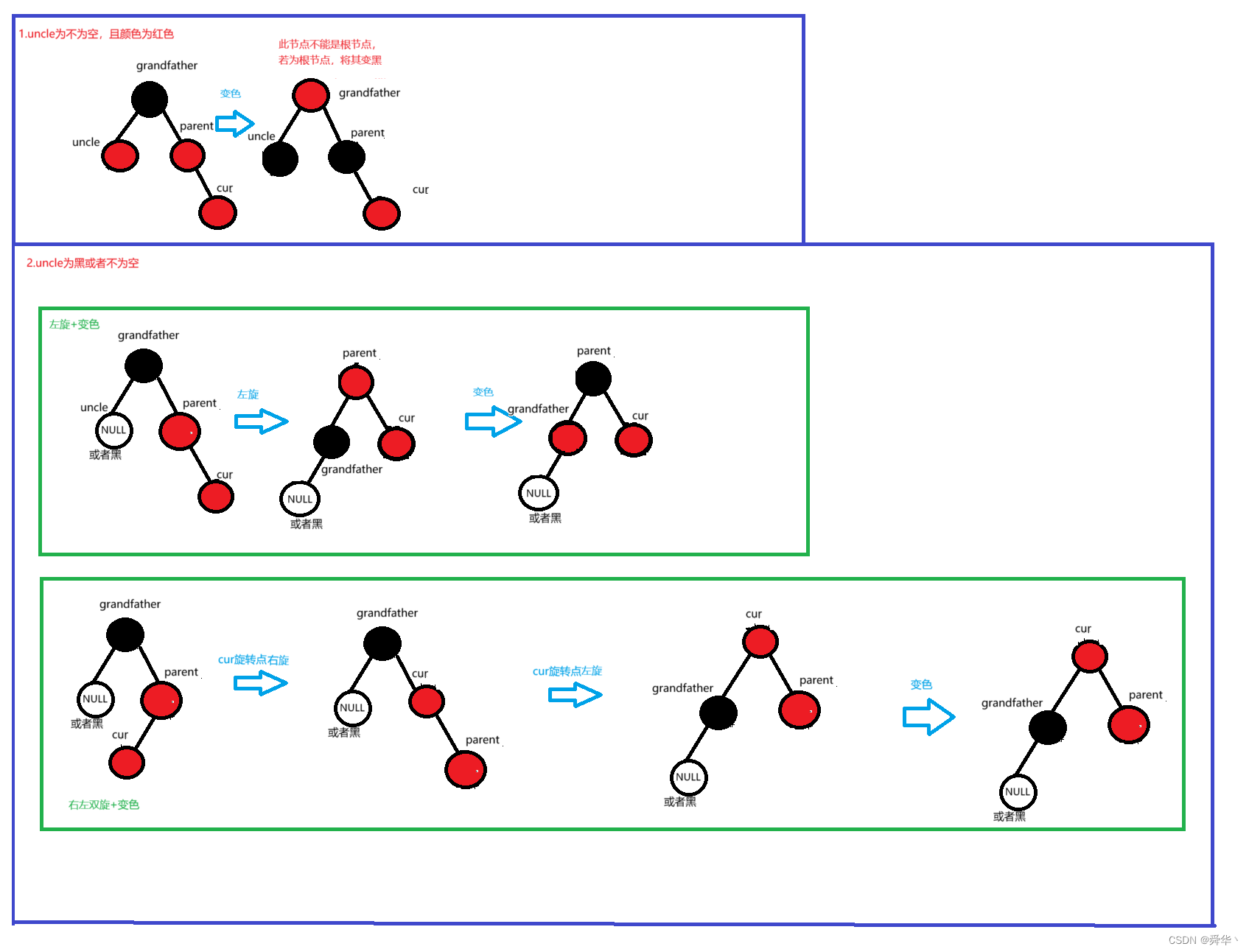
【数据结构】红黑树的插入与验证
文章目录 一、基本概念1.时代背景2. 基本概念3.基本性质 二、实现原理1. 插入1.1变色1.2旋转变色①左旋②右旋③右左双旋④左右双旋 2.验证 源码总结 一、基本概念 1.时代背景 1972年鲁道夫拜尔(Rudolf Bayer)发明了一种数据结构,这是一种特殊的B树4阶情况。这些树…...
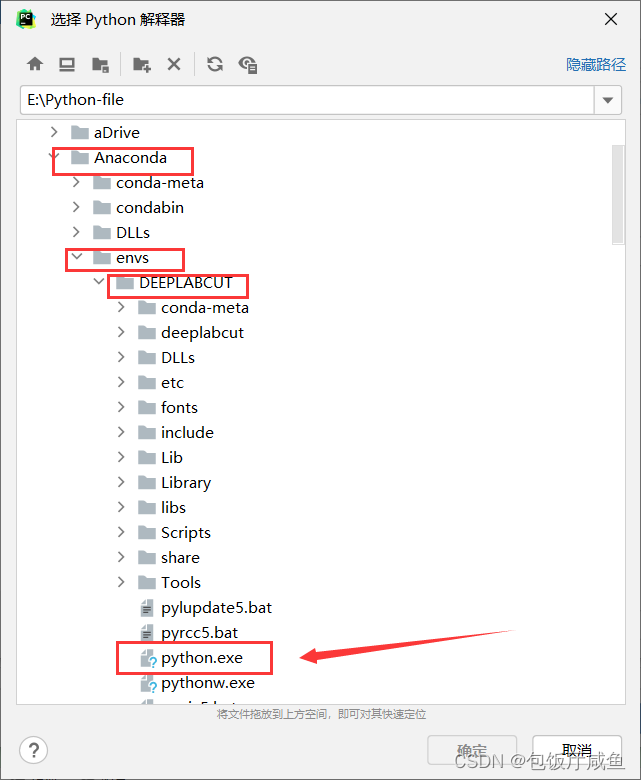
Pycharm----将Anaconda建立的环境导入
首先打开项目设置,点击添加 随后点击现有环境,点击三个。。。号进行添加 最后找到你Anaconda安装文件夹,envs找到你建立的环境名称,找到python.exe将它导入即可让现在的python环境为你建立的环境,同时还需要更改终端方…...

数字花园的指南针:微信小程序排名的提升之道
微信小程序,是一片数字花园,其中各种各样的小程序竞相绽放,散发出各自独特的芬芳。在这个花园中,排名优化就像是精心照料花朵的园丁,让我们一同走进这个数字花园,探寻如何提升微信小程序的排名优化…...

LRU与LFU的c++实现
LRU 是时间维度上最少使用 维持一个链表,最近使用的放在表头 淘汰表尾 LFU 是实际使用频率的最少使用 每一个对应的频率维持一个链表, 淘汰最低频率的最后一个 1. LRU LRU(Least Recently Used,最近最少使用)是一种常…...

什么是Docker和Docker-Compose?
Docker的构成 Docker仓库:https://hub.docker.com Docker自身组件 Docker Client:Docker的客户端 Docker Server:Docker daemon的主要组成部分,接受用户通过Docker Client发出的请求,并按照相应的路由规则实现路由分发…...
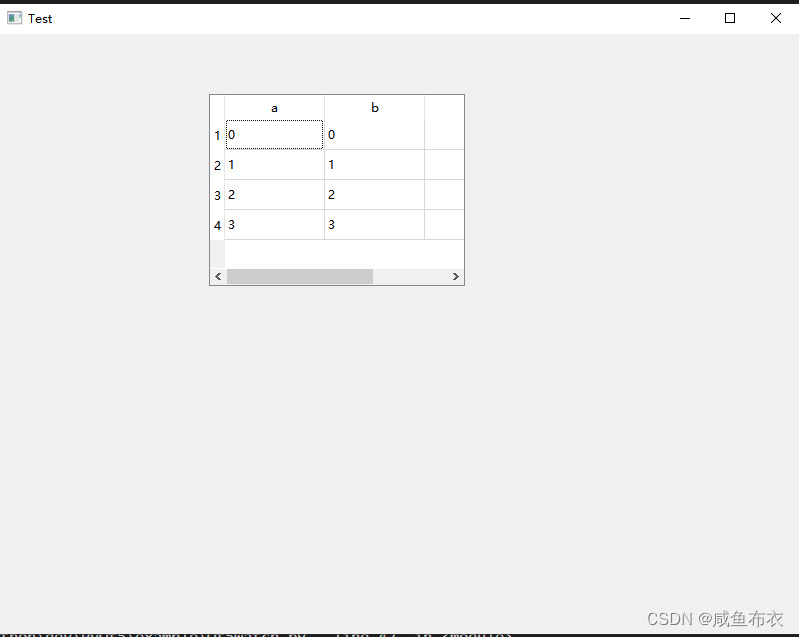
三.listview或tableviw显示
一.使用qt creator 转变类型 变形为listview或tableviw 二.导出ui文件为py文件 # from123.py 为导出 py文件 form.ui 为 qt creator创造的 ui 文件 pyuic5 -o x:\xxx\from123.py form.uifrom123.py listview # -*- coding: utf-8 -*-# Form implementation generated fro…...
【算法】一文带你从浅至深入门dp动态规划
文章目录 一、前言二、动态规划理论基础1、基本概念2、动态规划五部曲【✔】3、出错了如何排查? 三、实战演练🗡0x00 斐波那契数0x01 第N个泰波那契数0x02 爬楼梯0x03 三步问题0x04 使用最小花费爬楼梯⭐解法一解法二 0x05 解码方法* 四、总结与提炼 一、…...

超简单免费转换ape到flac
1. 安装最新版的ffmpeg 2. 安装cywin环境 3. 设置path到ffmpeg export PATH$PATH:"PATH/TO/FFMPEG/BIN" 4.到ape所在的目录,执行以下命令 find . -iname "*.ape" | while read line; do fb${line::-4}; fn"$fb.flac";echo ffm…...

JavaScript混淆加密
什么是JS混淆加密? JavaScript混淆加密是一种通过对源代码进行变换,使其变得难以理解和分析的技术。它的目标是增加攻击者破解代码的难度,同时保持代码的功能不受影响。混淆加密的目的是使代码难以逆向工程,从而防止攻击者窃取知…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
