Leetcode646. 最长数对链
Every day a Leetcode
题目来源:646. 最长数对链
解法1:动态规划
定义 dp[i] 为以 pairs[i] 为结尾的最长数对链的长度。
初始化时,dp 数组需要全部赋值为 1。
计算 dp[i] 时,可以先找出所有的满足 pairs[i][0]>pairs[j][1] 的 j,并求出最大的 dp[j],dp[i] 的值即可赋为这个最大值加一。
状态转移方程:dp[i] = max(dp[i], dp[j] + 1)
这种动态规划的思路要求计算 dp[i] 时,所有潜在的 dp[j] 已经计算完成,可以先将 pairs 数组进行排序来满足这一要求。
代码:
/** @lc app=leetcode.cn id=646 lang=cpp** [646] 最长数对链*/// @lc code=start
class Solution
{
public:int findLongestChain(vector<vector<int>> &pairs){// 特判if (pairs.empty())return 0;int n = pairs.size();// 状态数组,并初始化vector<int> dp(n + 1, 1);// dp[i]: 为 pairs[i] 结尾的最长数对链的长度sort(pairs.begin(), pairs.end());// 状态转移for (int i = 1; i <= n; i++)for (int j = 1; j < i; j++)if (pairs[j - 1][1] < pairs[i - 1][0])dp[i] = max(dp[i], dp[j] + 1);return dp[n];}
};
// @lc code=end结果:
复杂度分析:
时间复杂度:O(n2),其中 n 为 pairs 数组的长度。排序的时间复杂度为 O(nlogn),两层 for 循环的时间复杂度为 O(n2)。
空间复杂度:O(n),dp 数组的空间复杂度为 O(n)。
解法2:最长递增子序列
方法一实际上是「300. 最长递增子序列」的动态规划解法,这个解法可以改造为贪心 + 二分查找的形式。
用一个数组 arr 来记录当前最优情况,arr[i] 就表示长度为 i+1 的数对链的末尾可以取得的最小值,遇到一个新数对时,先用二分查找得到这个数对可以放置的位置,再更新 arr。
代码:
/** @lc app=leetcode.cn id=646 lang=cpp** [646] 最长数对链*/// @lc code=start// 动态规划// class Solution
// {
// public:
// int findLongestChain(vector<vector<int>> &pairs)
// {
// // 特判
// if (pairs.empty())
// return 0;
// int n = pairs.size();
// // 状态数组,并初始化
// vector<int> dp(n + 1, 1);
// // dp[i]: 为 pairs[i] 结尾的最长数对链的长度
// sort(pairs.begin(), pairs.end());
// // 状态转移
// for (int i = 1; i <= n; i++)
// for (int j = 1; j < i; j++)
// if (pairs[j - 1][1] < pairs[i - 1][0])
// dp[i] = max(dp[i], dp[j] + 1);
// return dp[n];
// }
// };// 贪心 + 二分查找class Solution
{
public:int findLongestChain(vector<vector<int>> &pairs){sort(pairs.begin(), pairs.end());vector<int> dp;for (auto &pair : pairs){int x = pair[0], y = pair[1];if (dp.empty() || dp.back() < x)dp.push_back(y);else{auto iter = lower_bound(dp.begin(), dp.end(), x);*iter = min(*iter, y);}}return dp.size();}
};
// @lc code=end结果:
复杂度分析:
时间复杂度:O(nlogn),其中 n 为 pairs 的长度。排序的时间复杂度为 O(nlogn),二分查找的时间复杂度为 O(nlogn),二分的次数为 O(n)。
空间复杂度:O(n),数组 arr 的长度最多为 O(n)。
解法3:贪心
要挑选最长数对链的第一个数对时,最优的选择是挑选第二个数字最小的,这样能给挑选后续的数对留下更多的空间。
挑完第一个数对后,要挑第二个数对时,也是按照相同的思路,是在剩下的数对中,第一个数字满足题意的条件下,挑选第二个数字最小的。
按照这样的思路,可以先将输入按照第二个数字排序,然后不停地判断第一个数字是否能满足大于前一个数对的第二个数字即可。
代码:
class Solution
{
private:// 排序函数static bool cmp(const vector<int> &a, const vector<int> &b){return a[1] < b[1];}public:int findLongestChain(vector<vector<int>> &pairs){int cur = INT_MIN, res = 0;sort(pairs.begin(), pairs.end(), cmp);for (auto &pair : pairs){int x = pair[0], y = pair[1];if (cur < x){cur = y;res++;}}return res;}
};
结果:
复杂度分析:
时间复杂度:O(nlogn),其中 n 为 pairs 的长度。排序的时间复杂度为 O(nlogn)。
空间复杂度:O(logn),为排序的空间复杂度。
相关文章:

Leetcode646. 最长数对链
Every day a Leetcode 题目来源:646. 最长数对链 解法1:动态规划 定义 dp[i] 为以 pairs[i] 为结尾的最长数对链的长度。 初始化时,dp 数组需要全部赋值为 1。 计算 dp[i] 时,可以先找出所有的满足 pairs[i][0]>pairs[j]…...

Windows 下安装NPM
第一步: 下载node.js的windows版 当前最新版本是https://nodejs.org/dist/ 第二步:设置环境变量 把node.exe所在目录加入到PATH环境变量中。 配置成功后可以在CMD中通过node --version 看到node.js对应的版本号 C:\Users\fn>node --version v6.10.2 第三步: 安装git 直接…...

【ARM CoreLink 系列 2 -- CCI-400 控制器简介】
文章目录 CCI-400 介绍DVM 机制介绍DVM 消息传输过程TOKEN 机制介绍 下篇文章:ARM CoreLink 系列 3 – CCI-550 控制器介绍 CCI-400 介绍 CCI(Cache Coherent Interconnect)是ARM 中 的Cache一致性控制器。 CCI-400 将 Interconnect 和coh…...

LeetCode(力扣)77. 组合Python
LeetCode77. 组合 题目链接代码 题目链接 https://leetcode.cn/problems/combinations/description/ 代码 class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result []return self.backtracking(n, k, 1, [], result)def backtracking(self, n, k…...
uniapp h5 微信缓存,解决版本更新还是旧版本
文章目录 一、微信缓存是什么?二、如何解决1.打包入口文件解决2.给请求url加时间戳3.给打包的js文件添加时间戳并修改打包后的css文件夹 总结 一、微信缓存是什么? 微信缓存是指微信客户端为了提高用户的使用体验,会在用户使用微信过程中将一…...

Nacos——Distro一致性协议
Nacos——Distro一致性协议 1. 理论 一致性一直都是分布式系统中绕不开的话题。根据CAP中,要么CP(保证强一致性牺牲可用性),要么AP(最终一致性来保证可用性),在市面上也有几种一致性算法,像Paxos,Raft,Zoo…...
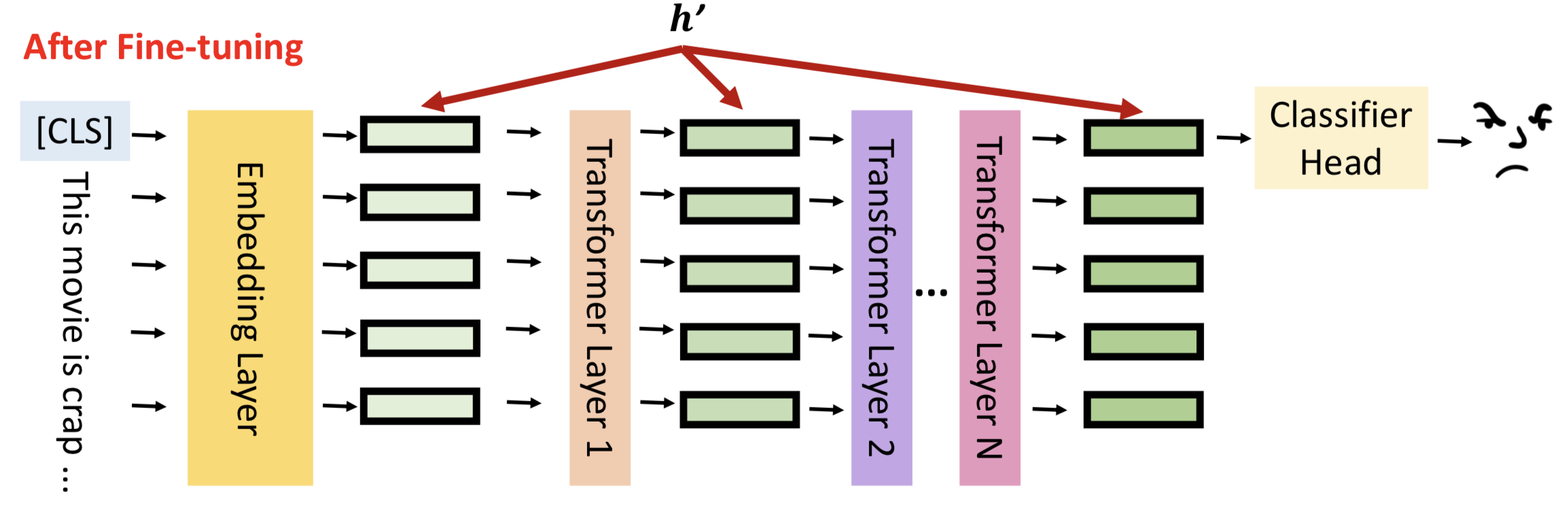
大模型参数高效微调PEFT的理解和应用
简介 近年的大型语言模型(也被称作基础模型),大多是采用大量资料数据和庞大模型参数训练的结果,比如常见的ChatGPT3有175B的模型参数量。随着Large Language Model(LLM)的横空出世,网络模型对常见问题的解答有了很强的…...
工作游戏时mfc140u.dll丢失的解决方法,哪个方法可快速修复mfc140u.dll问题
在 Windows 操作系统中,mfc140u.dll 文件是非常重要的一个组件,许多基于 MFC(Microsoft Foundation Classes)的程序都需要依赖这个文件。然而,有些用户在运行这些程序时可能会遇到mfc140u.dll丢失的问题,导…...
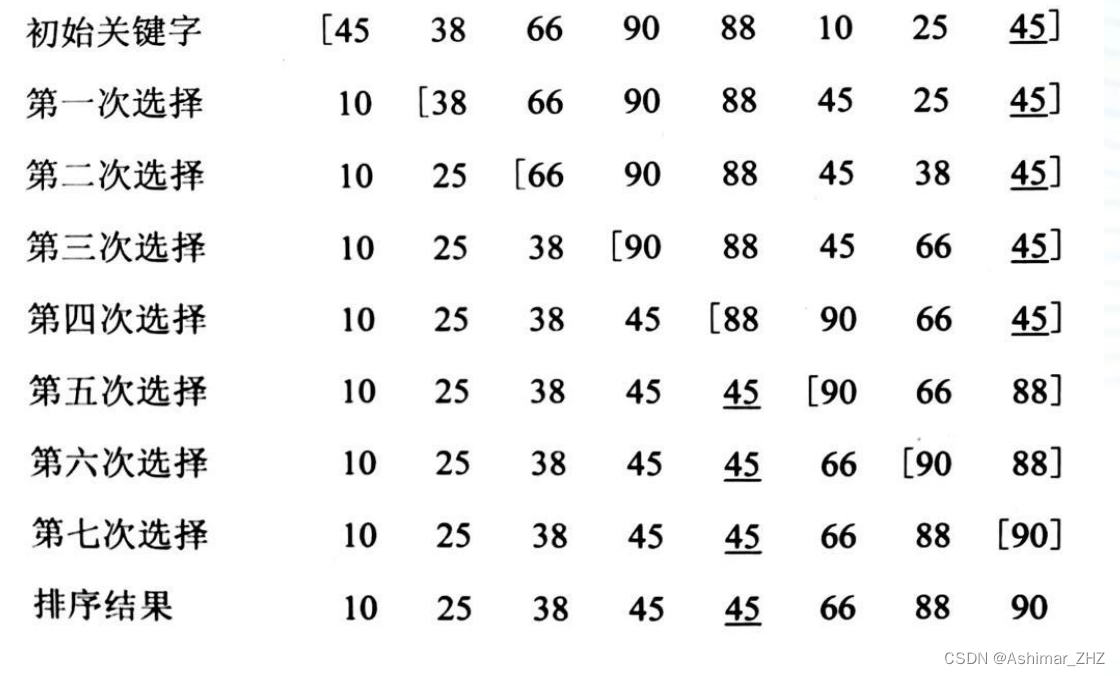
选择排序——直接选择排序
直接选择排序:(以重复选择的思想为基础进行排序) 1、简述 顾名思义就是选出一个数,再去抉择放哪里去。 设记录R1,R2…,Rn,对i1,2,…,n-1,重复下…...
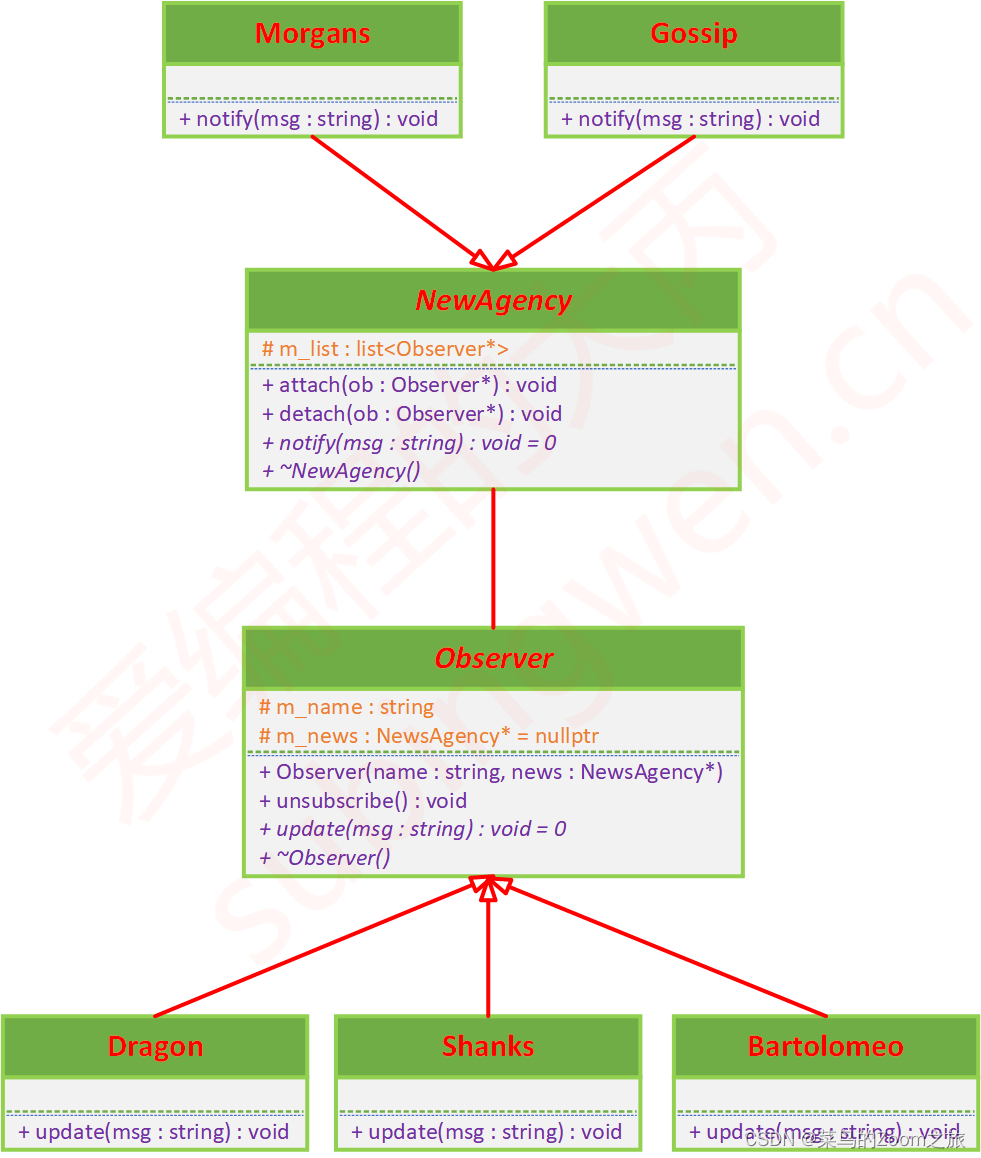
【C++基础】观察者模式(“发布-订阅”模式)
本文参考:观察者模式 - 摩根斯 | 爱编程的大丙 观察者模式允许我们定义一种订阅机制,可在对象事件发生时通知所有的观察者对象,使它们能够自动更新。观察者模式还有另外一个名字叫做“发布-订阅”模式。 发布者: 添加订阅者&…...

从业多年,我总结出软件测试工程师必须掌握的技能,你不可错过!
经常会有小伙伴询问:“测试工程师有哪些必须要掌握的技能?”这是一个非常大的课题,因为每个人从事的行业不同、岗位不同,需要掌握的技能自然也不一样。 今天小编就从不同岗位、不同行业两个大方面,来讲讲软件测试工程师…...

【nerfStudio】5-nerfStudio导出3D Mesh模型
几何图形的导出 在这里我们将介绍如何从nerfstudio中导出点云和网格。您将使用的主要命令是ns-export。我们将点云导出为.ply文件,纹理网格导出为.obj文件。 导出网格 1. TSDF融合 TSDF(截断有符号距离函数)融合是一种使用深度图像提取表面网格的算法。此方法适用于所有…...

重要公告|投票委托已经上线,应该如何选择社区代表?
社区代表是Token持有者委托投票权的个人或团体,可以代表Token持有者在Moonbeam治理中投票。委托是可选的,允许代表在治理过程中代表更大比例的Token和Token持有者。相比社区代表,不愿投票的Token持有者可以将投票权委托给社区代表,…...
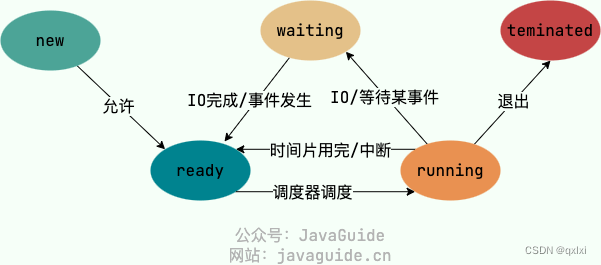
【操作系统】聊聊进程、线程、协程
进程内部有那些数据 为什么创建进程的成本高 进程和线程 进程是资源分配的基本单位,而线程是程序执行的基本单位,一个是从资源分配的角度看,另一个是执行角度。 那么进程和程序的区别是什么? 程序,一段代码ÿ…...

springboot 下 activiti 7会签配置与实现
流程图配置 会签实现须在 userTask 节点下的 multi instance 中配置 collection 及 completion condition; collection 会签人员列表;element variable 当前会签变量名称,类似循环中的 item;completion condition: 完成条件。 ${taskExecutionServiceIm…...

RK3399平台开发系列讲解(内核调试篇)spidev_test工具使用
🚀返回专栏总目录 文章目录 一、环境二、执行测试三、回环测试四、字节发送测试五、32位数据发送测试沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 在 Linux 系统上,“spidev_test” 是一个用于测试和配置 SPI(Serial Peripheral Interface)设备的命令行工具。…...
)
点云从入门到精通技术详解100篇-自适应点云局部邻域特征的特征提取与配准(续)
目录 3.4 深度相机误差建模 3.5 实验结果及分析 3.5.1 TOF 相机平面畸变校正 3.5.2 TOF 相机深度误差校正...

VBA技术资料MF52:VBA_在Excel中突出显示前 10 个值
【分享成果,随喜正能量】一言之善,重于千金。善良不分大小,有时候你以为的一句话,小小的举手之劳,也可能就是别人的救赎!不要吝啬你的善良,因为你永远不知道那小小的善良能给多少人带来光明。。…...

leetcode做题笔记134. 加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。 给定两个整数数组 gas 和 cost &…...
Allegro166版本如何在颜色管理器中实时显示层面操作指导
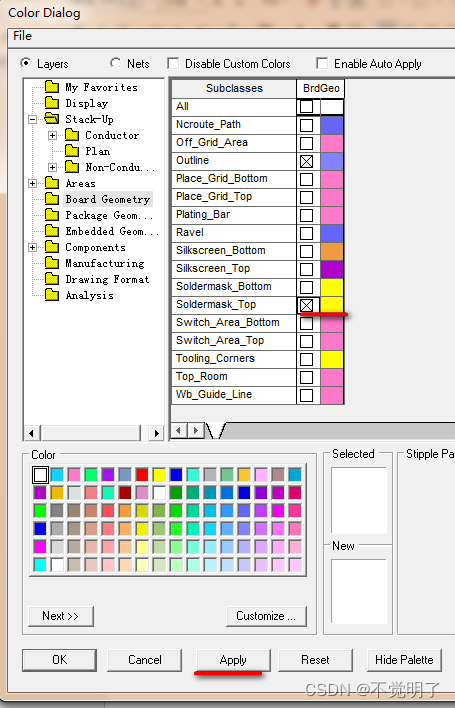
Allegro166版本如何在颜色管理器中实时显示层面操作指导 在用Allegro166进行PCB设计的时候,需要在颜色管理器中频繁的开关层面。但是166不像172一样在颜色管理器中可以实时的开关层面,如下图 需要打开Board Geometry/Soldermask_top层,首先需要勾选这个层面,再点击Apply即…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
