QIfw制作软件安装程序
前言
Qt Installer Framework是Qt默认包的发布框架。它很方便,使用静态编译Qt制作而成。从Qt的下载地址中下载Qt Installer Framework,地址是:http://download.qt.io/official_releases/qt-installer-framework/ 。支持我们自定义一些我们需要的东西包括页面、交互等。
框架介绍
组成部分:config文件夹、packages文件夹
config/config.xml:
<?xml version="1.0" encoding="UTF-8"?>
<Installer><Name>在线快乐交友平台</Name><Version>1.0.0</Version><Title>在线快乐交友平台</Title><Publisher>快乐交友有限公司</Publisher><ProductUrl>http://www.getfriend.com</ProductUrl><!-- 64*64 --><Logo>logo.png</Logo><Watermark>water.png</Watermark><StartMenuDir>happy getFriend</StartMenuDir>&相关文章:

QIfw制作软件安装程序
前言 Qt Installer Framework是Qt默认包的发布框架。它很方便,使用静态编译Qt制作而成。从Qt的下载地址中下载Qt Installer Framework,地址是:http://download.qt.io/official_releases/qt-installer-framework/ 。支持我们自定义一些我们需要的东西包括页面、交互等。 框…...
【C++】C++入门(上)
前言: C是在C语言的基础上不断添加东西形成的一门语言,在C语言的基础上引入了面向对象的思想。因此C既是面向对象的语言,也是面向过程的语言。因为C是以C语言为基础的,所以基本上C兼容所有的C语言。目前最常用的版本是C98和C11这两…...
)
5. Kimball维度建模常用术语及概念(一)
文章目录维度建模过程相关概念1. 收集业务需求与数据实现2. 协作维度建模研讨3. 四步骤维度设计过程4. 业务过程5. 粒度6. 描述环境的维度7. 用于度量的事实8. 维度模型事实表技术术语1. 事实表结构2. 可加、半可加、不可加事实3. 事实表中的空值4. 一致性事实5. 事务事实表6. …...

内核调试之Panic-Oops日志分析
这部分我们接着之前的思考,看看内核异常日志的分析。 1 Panic 调试 2 Oops调试 内核出现Panic或Oops错误,如何分析定位问题原因? 首先,保留现场,如下所示为一次非法虚拟地址访问错误。 EXT4-fs (sdc3): recovery c…...
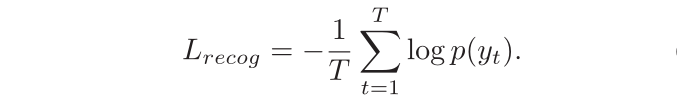
论文解读 | [AAAI2020] 你所需要的是边界:走向任意形状的文本定位
目录 1、研究背景 2、研究的目的 3、方法论 3.1 Boundary Point Detection Network(BPDN) 3.2 Recognition Network 3.3 Loss Functions 4、实验及结果 论文连接:https://ojs.aaai.org/index.php/AAAI/article/view/6896 1、研究背景 最近,旨在…...

数据挖掘流程简单示例10min
数据挖掘流程简单示例10min 套路: 准备数据实现算法测试算法 任务1:亲和性分析 如果一个顾客买了商品X,那么他们可能愿意买商品Y衡量方法: 支持度support : 所有买X的人数 置信度confidence : 所有买X和Y的人数所有买X的人数…...
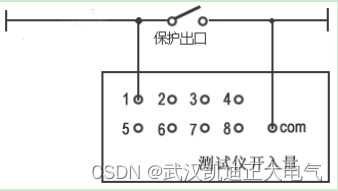
KDJB1200六相继电保护测试仪
一、概述 KDJB1200继电保护测试仪是在参照电力部颁发的《微机型继电保护试验装置技术条件(讨论稿)》的基础上,广泛听取用户意见,总结目前国内同类产品优缺点,充分使用现代新的的微电子技术和器件实现的一种新型小型化微机继电保护测试仪。可…...
从WEB到PWA 开发-发布-安装
见意如题!本文主要来说说PWA开发!作为一个前端程序员,在没有任何Android/IOS的开发情况下,想想我们有多少种方法来开发一个原生移动应用程序!我们可以有非原生、混合开发,PWA等等手段。类似uniappÿ…...

FPGA纯vhdl实现MIPI CSI2 RX视频解码输出,OV13850采集,提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...

《NFL橄榄球》:卡罗来纳黑豹·橄榄1号位
卡罗来纳黑豹(英语:Carolina Panthers)是一支位于北卡罗来纳州夏洛特的职业美式橄榄球球队。他们是国家美式橄榄球联合会的南区其中一支球队。他们与杰克逊维尔美洲虎在1995年加入NFL,成为扩充球队。 2018年球队市值为23亿美元&am…...
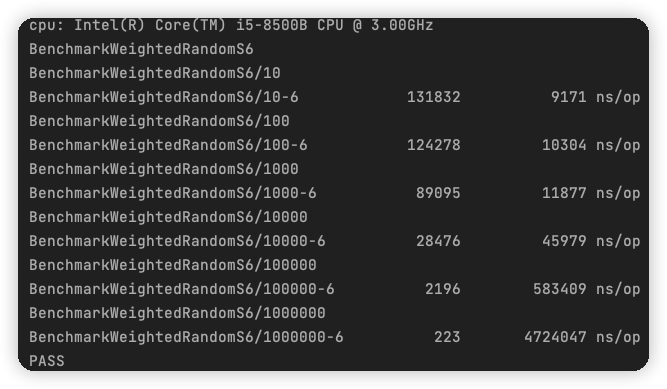
我说我为什么抽不到SSR,原来是这段代码在作祟...
本文是龚国玮所写,熊哥有所新增修改删减,原文见文末。 我说我为什么抽不到SSR,原来是加权随机算法在作祟 阅读本文需要做好心理准备,建议带着深究到底的决心和毅力进行学习! 灵魂拷问 为什么有 50% 的几率获得金币&a…...

MySQL MGR 集群新增节点
前言 服务器规划现状(CentOS7.x) IP地址主机名部署角色192.168.x.101mysql01mysql192.168.x.102mysql02mysql192.168.x.103mysql03mysql192.168.x.104proxysql01proxysql、keepalived192.168.x.105proxysql02proxysql、keepalived 新增服务器IP&#x…...

【单目标优化算法】蜣螂优化算法(Dung beetle optimizer,DBO)(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
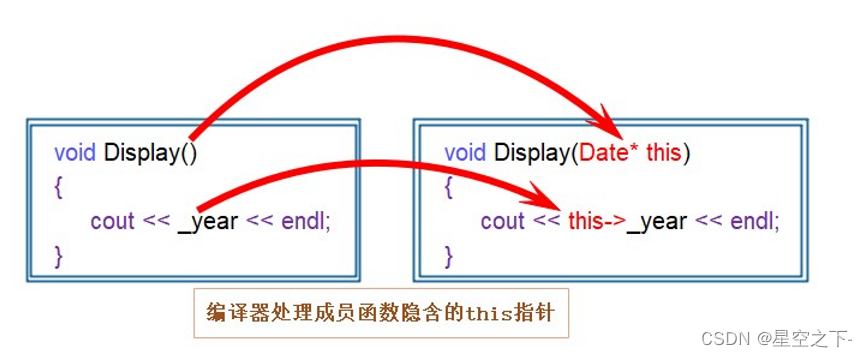
【C++】类和对象入门必知
面向过程和面向对象的初步认识类的引入类的定义类的访问限定符封装类的作用域类的实例化类对象模型this指针C语言和C实现Stack的对比面向过程和面向对象的初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解…...

day38 动态规划 | 509、斐波那契数 70、爬楼梯 746、使用最小花费爬楼梯
题目 509、斐波那契数 斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其…...

2023年备考软考必须知道的6件事
不知不觉,距离2023年上半年软考也只有不到100天的时间了,报名入口也将在3月13日正式开通,你是正在犹豫是否参加考试? 还是已经开始着手准备复习? 关于软考考试你还有哪些疑问? 2023年备考软考必须知道的6件事,建议收藏…...

GLOG如何控制输出的小数点位数
1 问题 在小白的蹩脚翻译演绎型博文《GLOG从入门到入门》中,有位热心读者提问说:在保存日志时,浮点型变量的小数位数如何设置? 首先感谢这位“嘻嘻哈哈的地球人”赏光阅读了小白这不太通顺的博客文章,并提出了一个很…...
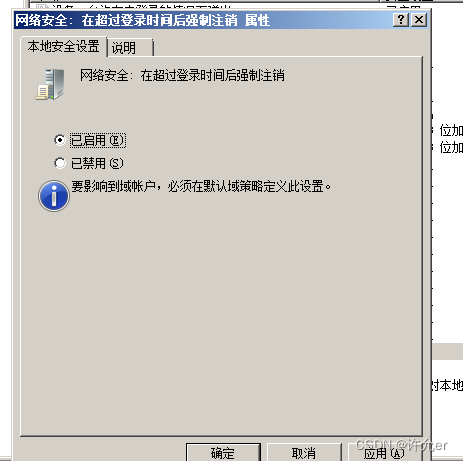
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题A(6)
目录 模块A 基础设施设置与安全加固 一、项目和任务描述: 二、服务器环境说明 三、具体任务(每个任务得分以电子答题卡为准) A-1任务一:登录安全加固(Windows) 1.密码策略 a.密码策略必须同时满足大小…...

Safety-Gym环境配置与安
官网: https://github.com/openai/safety-gym https://github.com/openai/safety-starter-agents 一、安装依赖环境配置 建议使用python 3.7及以下环境,因为官方的safety-rl是基于tensorflow1.13.1实现,而tensorflow1.13.1只能支持python…...
3月再不跳槽,就晚了
从时间节点上来看,3月、4月是每年跳槽的黄金季! 以 BAT 为代表的互联网大厂,无论是薪资待遇、还是平台和福利,都一直是求职者眼中的香饽饽,“大厂经历” 在国内就业环境中无异于一块金子招牌。在这金三银四的时间里&a…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
