华为OD机试真题Python实现【RSA 加密算法】真题+解题思路+代码(20222023)
相关文章:
)
华为OD机试真题Python实现【RSA 加密算法】真题+解题思路+代码(20222023)
RSA 加密算法 题目 RSA 加密算法在网络安全世界中无处不在 它利用了极大整数因数分解的困难度,数据越大安全系数越高 给定了一个32位正整数,请对其进行因数分解 找出哪两个素数的乘积 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输…...
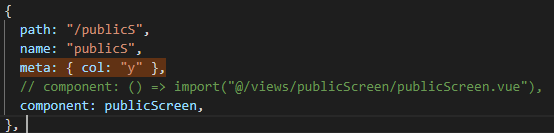
App.vue中读取不到路由的信息
问题: 首先定义了一个路由,并且在路由元里面存储了一个变量,在App.vue里面访问这个变量的时候却显示undefined!在路由对应的组件中却能访问到! 定义的路由元信息: 为啥访问不到…,懵逼的我在App.vue里…...

Lambda表达式详解
文章目录1、Lambda表达式简介2、如何使用Lambda表达式3、在哪里使用Lambda表达式3.1 函数式接口3.2函数描述符4、四大核心函数式接口4.1 Predicate4.2 Consumer4.3 Function4.4 Supplier5、方法引用5.1 方法引用的使用情况6、构造器引用7、数组引用8、复合Lambda表达式的有用方…...
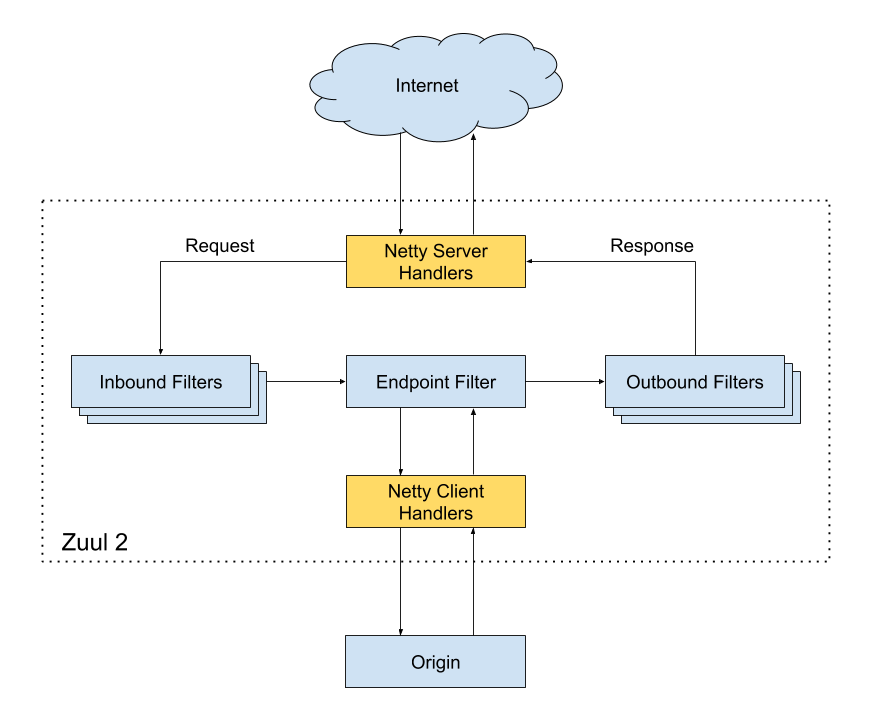
网关的通用设计框架
概念 网关,很多地方将网关比如成门, 没什么问题, 但是需要区分网关与网桥的区别。 网桥:工作在数据链路层,在不同或相同类型的LAN之间存储并转发数据帧,必要时进行链路层上的协议转换。可连接两个或多个网络…...
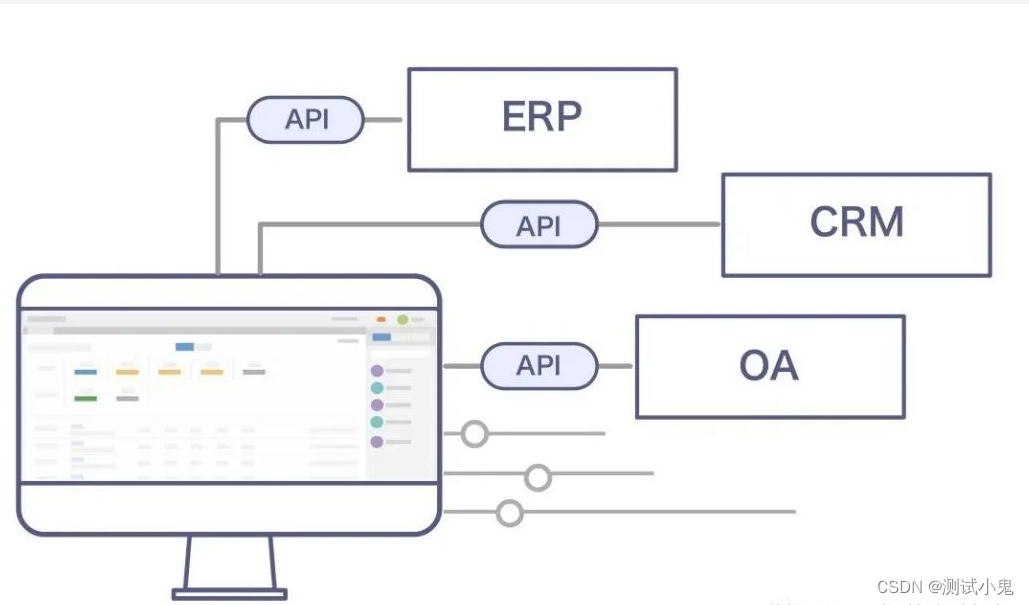
API 接口应该如何设计?如何保证安全?如何签名?如何防重?
说明:在实际的业务中,难免会跟第三方系统进行数据的交互与传递,那么如何保证数据在传输过程中的安全呢(防窃取)?除了https的协议之外,能不能加上通用的一套算法以及规范来保证传输的安全性呢&am…...

LeetCode-131. 分割回文串
目录题目思路回溯题目来源 131. 分割回文串 题目思路 切割问题类似组合问题。 例如对于字符串abcdef: 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…。切割问题:切割一个a之后&…...
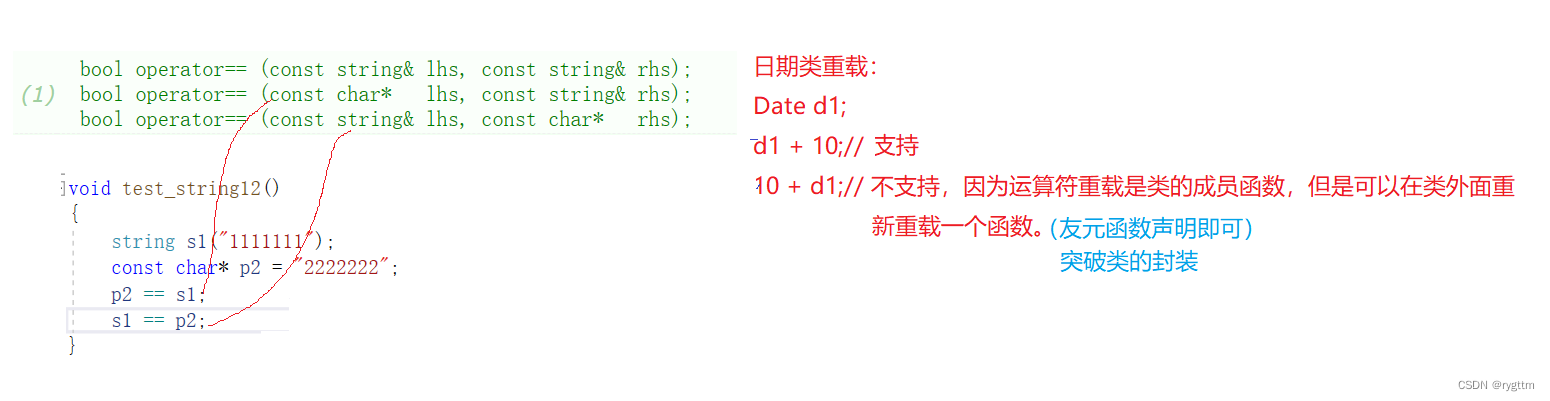
【C++】string类的基本使用
层楼终究误少年,自由早晚乱余生。你我山前没相见,山后别相逢… 文章目录一、编码(ascll、unicode字符集、常用的utf-8编码规则、GBK)1.详谈各种编码规则2.汉字在不同的编码规则中所占字节数二、string类的基本使用1.string类的本质…...
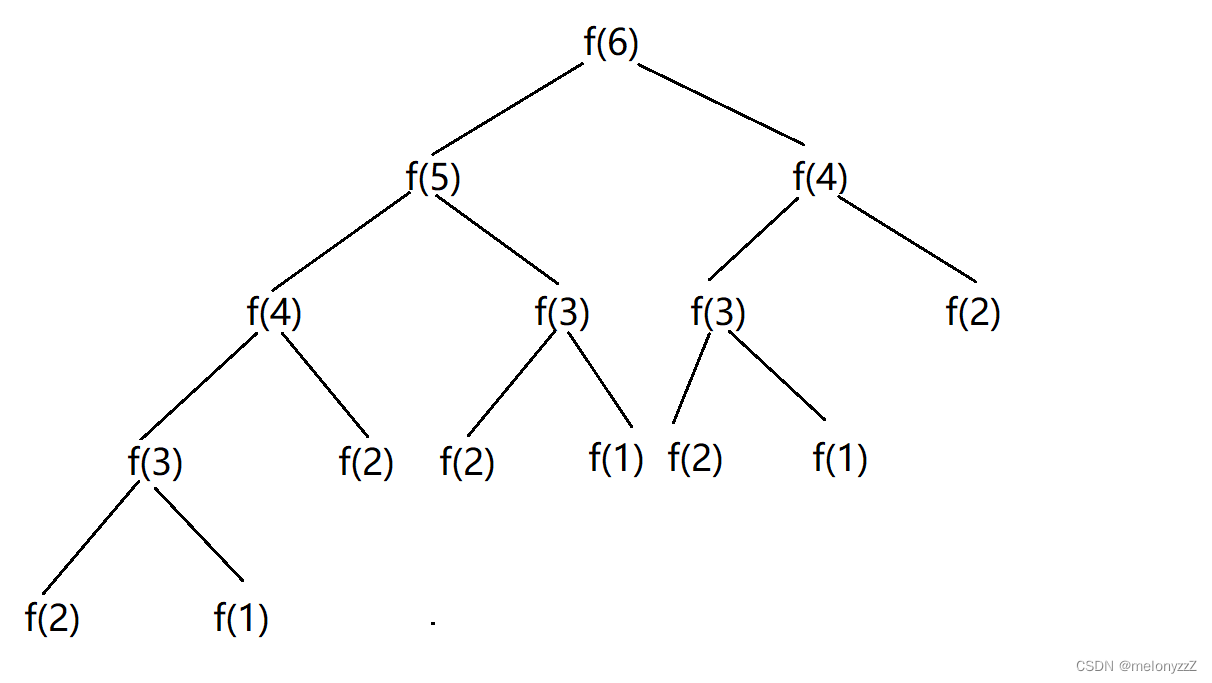
【第一章 - 绪论】- 数据结构(近八千字详解)
目录 一、 数据结构的研究内容 二、基本概念和术语 2.1 - 数据、数据元素、数据项和数据对象 2.2 - 数据结构 2.2.1 - 逻辑结构 2.2.2 - 存储结构 2.3 - 数据类型和抽象数据类型 三、抽象数据类型的表现与实现 四、算法和算法分析 4.1 - 算法的定义及特性 4.2 - 评价…...

QIfw制作软件安装程序
前言 Qt Installer Framework是Qt默认包的发布框架。它很方便,使用静态编译Qt制作而成。从Qt的下载地址中下载Qt Installer Framework,地址是:http://download.qt.io/official_releases/qt-installer-framework/ 。支持我们自定义一些我们需要的东西包括页面、交互等。 框…...
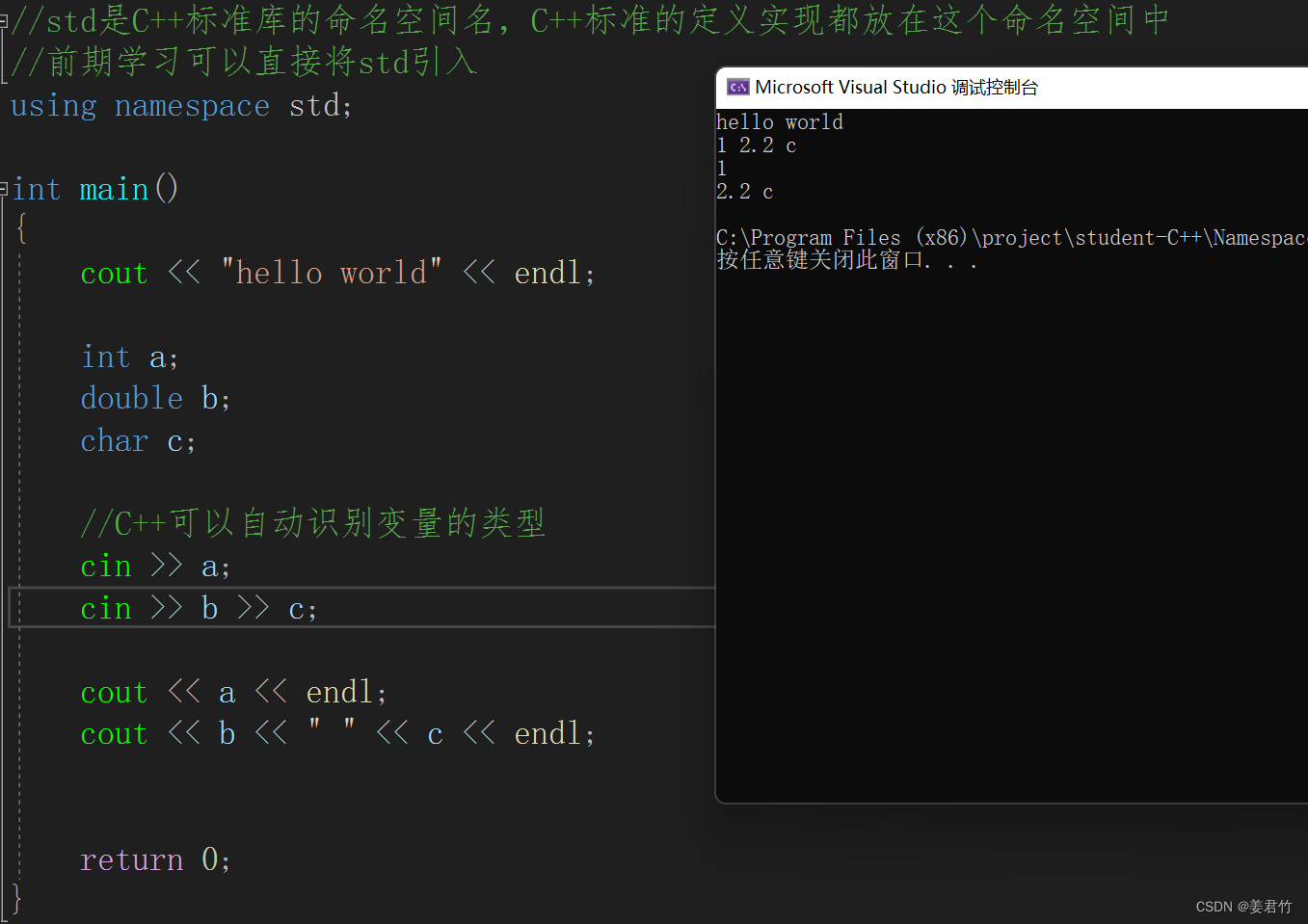
【C++】C++入门(上)
前言: C是在C语言的基础上不断添加东西形成的一门语言,在C语言的基础上引入了面向对象的思想。因此C既是面向对象的语言,也是面向过程的语言。因为C是以C语言为基础的,所以基本上C兼容所有的C语言。目前最常用的版本是C98和C11这两…...
)
5. Kimball维度建模常用术语及概念(一)
文章目录维度建模过程相关概念1. 收集业务需求与数据实现2. 协作维度建模研讨3. 四步骤维度设计过程4. 业务过程5. 粒度6. 描述环境的维度7. 用于度量的事实8. 维度模型事实表技术术语1. 事实表结构2. 可加、半可加、不可加事实3. 事实表中的空值4. 一致性事实5. 事务事实表6. …...

内核调试之Panic-Oops日志分析
这部分我们接着之前的思考,看看内核异常日志的分析。 1 Panic 调试 2 Oops调试 内核出现Panic或Oops错误,如何分析定位问题原因? 首先,保留现场,如下所示为一次非法虚拟地址访问错误。 EXT4-fs (sdc3): recovery c…...
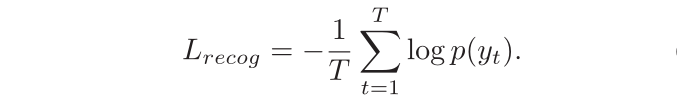
论文解读 | [AAAI2020] 你所需要的是边界:走向任意形状的文本定位
目录 1、研究背景 2、研究的目的 3、方法论 3.1 Boundary Point Detection Network(BPDN) 3.2 Recognition Network 3.3 Loss Functions 4、实验及结果 论文连接:https://ojs.aaai.org/index.php/AAAI/article/view/6896 1、研究背景 最近,旨在…...

数据挖掘流程简单示例10min
数据挖掘流程简单示例10min 套路: 准备数据实现算法测试算法 任务1:亲和性分析 如果一个顾客买了商品X,那么他们可能愿意买商品Y衡量方法: 支持度support : 所有买X的人数 置信度confidence : 所有买X和Y的人数所有买X的人数…...
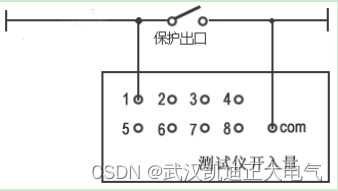
KDJB1200六相继电保护测试仪
一、概述 KDJB1200继电保护测试仪是在参照电力部颁发的《微机型继电保护试验装置技术条件(讨论稿)》的基础上,广泛听取用户意见,总结目前国内同类产品优缺点,充分使用现代新的的微电子技术和器件实现的一种新型小型化微机继电保护测试仪。可…...
从WEB到PWA 开发-发布-安装
见意如题!本文主要来说说PWA开发!作为一个前端程序员,在没有任何Android/IOS的开发情况下,想想我们有多少种方法来开发一个原生移动应用程序!我们可以有非原生、混合开发,PWA等等手段。类似uniappÿ…...

FPGA纯vhdl实现MIPI CSI2 RX视频解码输出,OV13850采集,提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...

《NFL橄榄球》:卡罗来纳黑豹·橄榄1号位
卡罗来纳黑豹(英语:Carolina Panthers)是一支位于北卡罗来纳州夏洛特的职业美式橄榄球球队。他们是国家美式橄榄球联合会的南区其中一支球队。他们与杰克逊维尔美洲虎在1995年加入NFL,成为扩充球队。 2018年球队市值为23亿美元&am…...
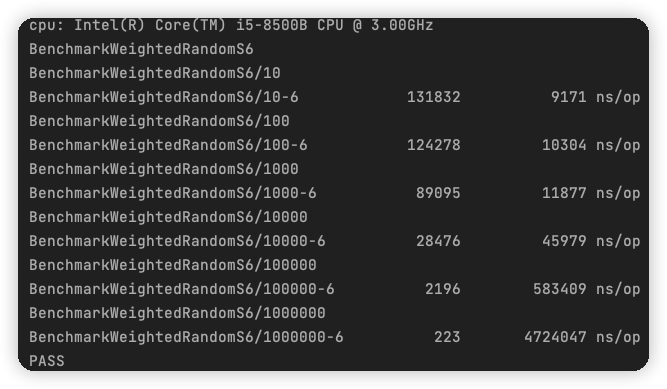
我说我为什么抽不到SSR,原来是这段代码在作祟...
本文是龚国玮所写,熊哥有所新增修改删减,原文见文末。 我说我为什么抽不到SSR,原来是加权随机算法在作祟 阅读本文需要做好心理准备,建议带着深究到底的决心和毅力进行学习! 灵魂拷问 为什么有 50% 的几率获得金币&a…...

MySQL MGR 集群新增节点
前言 服务器规划现状(CentOS7.x) IP地址主机名部署角色192.168.x.101mysql01mysql192.168.x.102mysql02mysql192.168.x.103mysql03mysql192.168.x.104proxysql01proxysql、keepalived192.168.x.105proxysql02proxysql、keepalived 新增服务器IP&#x…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
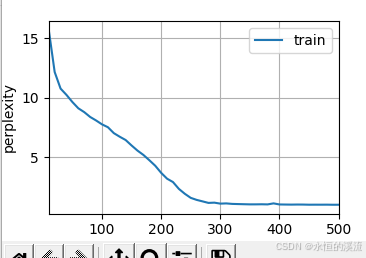
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

2025 后端自学UNIAPP【项目实战:旅游项目】7、景点详情页面【完结】
1、获取景点详情的请求【my_api.js】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http(/login/getWXSessionKey, {code,avatar}); };//…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...

2025年ESWA SCI1区TOP,自适应学习粒子群算法AEPSO+动态周期调节灰色模型,深度解析+性能实测
目录 1.摘要2.粒子群算法PSO原理3.改进策略4.结果展示5.参考文献6.代码获取7.算法辅导应用定制读者交流 1.摘要 能源数据的科学预测对于能源行业决策和国家经济发展具有重要意义,尤其是短期能源预测,其精度直接影响经济运行效率。为了更好地提高预测模型…...

基于python大数据的水文数据分析可视化系统
博主介绍:高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了多年的设计程序开发,开发过上千套设计程序,没有什么华丽的语言,只有实实在…...

c++ decltype关键字
decltype为类型推导关键字。 示例代码: // decltype也可用于函数模板编程: template<typename T, typename U> auto add(T t, U u) -> decltype(t u) {return t u; }// decltype推导函数返回类型 auto doubleNumFunc(int x) -> decltype(x * 2) {ret…...
