LeetCode-131. 分割回文串
目录
- 题目思路
- 回溯
题目来源
131. 分割回文串
题目思路
切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段…。
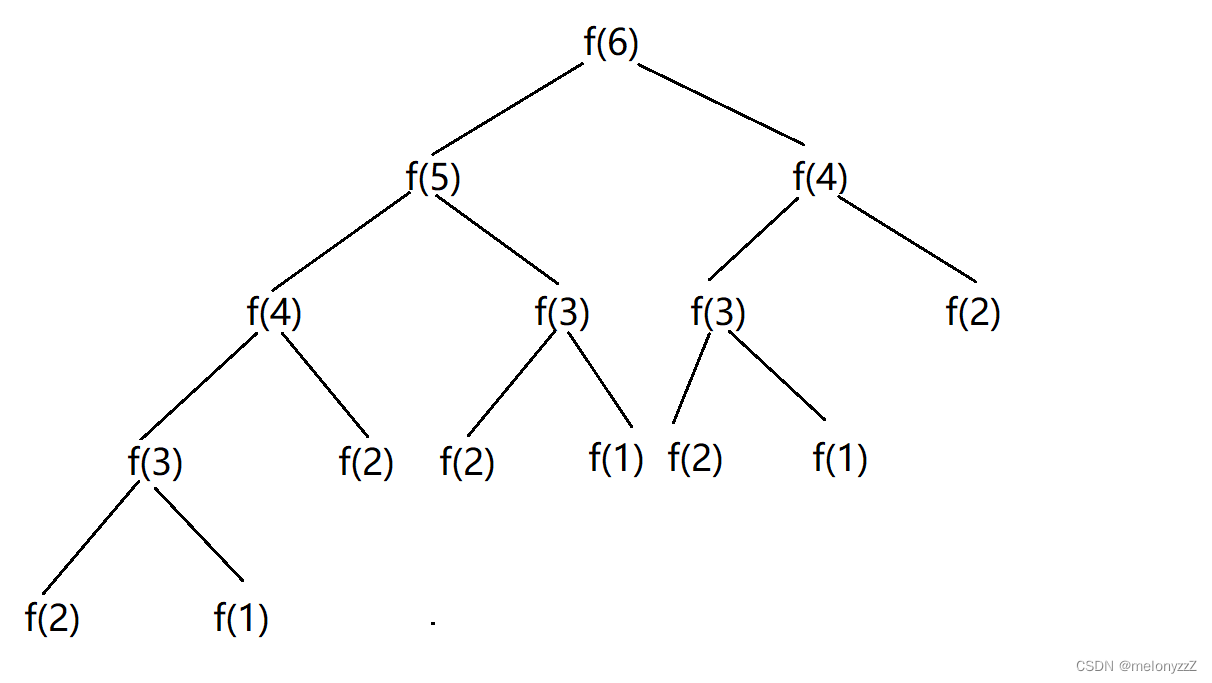
抽象为一棵树形结构

递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
回溯
- 1.递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。 (这两个参数可以放到函数参数里)
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
ArrayList<List<String>> result = new ArrayList<>();ArrayList<String> path = new ArrayList<>();void backTracking(String s,int startIndex)
- 2.递归函数终止条件

从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
终止条件代码如下:
if(startIndex >= s.length()){// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了result.add(new ArrayList(path));return;}
- 3.单层搜索的逻辑
来看看在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.length(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在path中,path用来记录切割过的回文子串。
for(int i = startIndex;i<s.length();i++){//如果是回文子串,则记录if(isPalindrome(s,startIndex,i)){String str = s.substring(startIndex,i+1);path.add(str);}else{continue;}//起始位置后移,保证不重复backTracking(s,i+1);path.remove(path.size()-1);}
注意切割过的位置,不能重复切割,所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1。
判断回文子串
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
private boolean isPalindrome(String s,int start,int end){for(int i=start,j=end;i<j;i++,j--){if(s.charAt(i) != s.charAt(j)){return false;}}return true;}
整体代码
class Solution {ArrayList<List<String>> result = new ArrayList<>();ArrayList<String> path = new ArrayList<>();public List<List<String>> partition(String s) {if(s == null || s.length() < 1){return result;}backTracking(s,0);return result;}public void backTracking(String s,int startIndex){// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if(startIndex >= s.length()){result.add(new ArrayList(path));return;}for(int i = startIndex;i<s.length();i++){//如果是回文子串,则记录if(isPalindrome(s,startIndex,i)){String str = s.substring(startIndex,i+1);path.add(str);}else{continue;}//起始位置后移,保证不重复backTracking(s,i+1);path.remove(path.size()-1);}}private boolean isPalindrome(String s,int start,int end){for(int i=start,j=end;i<j;i++,j--){if(s.charAt(i) != s.charAt(j)){return false;}}return true;}
}

相关文章:

LeetCode-131. 分割回文串
目录题目思路回溯题目来源 131. 分割回文串 题目思路 切割问题类似组合问题。 例如对于字符串abcdef: 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…。切割问题:切割一个a之后&…...
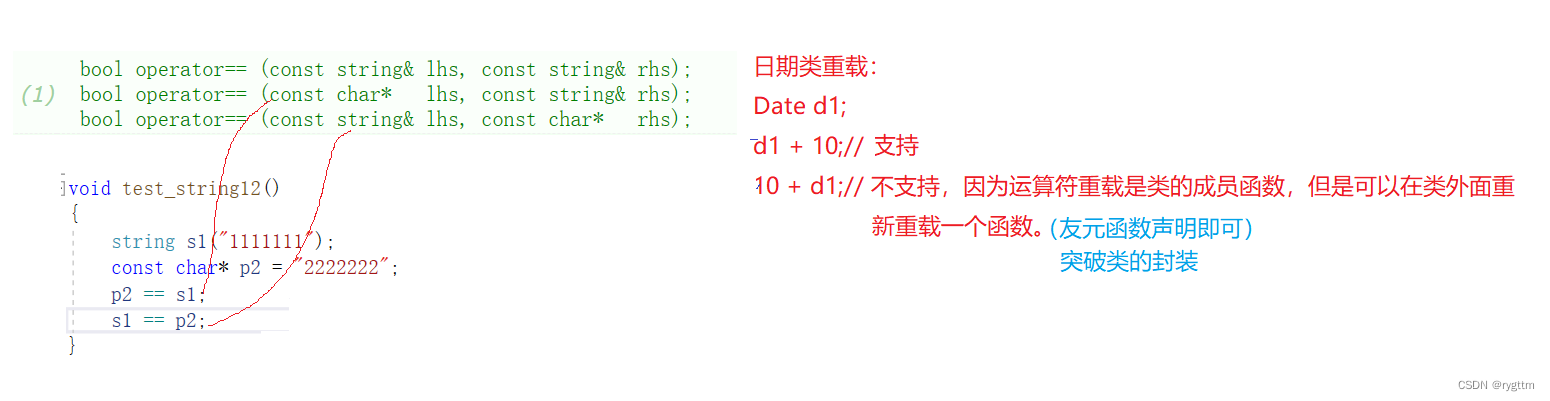
【C++】string类的基本使用
层楼终究误少年,自由早晚乱余生。你我山前没相见,山后别相逢… 文章目录一、编码(ascll、unicode字符集、常用的utf-8编码规则、GBK)1.详谈各种编码规则2.汉字在不同的编码规则中所占字节数二、string类的基本使用1.string类的本质…...
【第一章 - 绪论】- 数据结构(近八千字详解)
目录 一、 数据结构的研究内容 二、基本概念和术语 2.1 - 数据、数据元素、数据项和数据对象 2.2 - 数据结构 2.2.1 - 逻辑结构 2.2.2 - 存储结构 2.3 - 数据类型和抽象数据类型 三、抽象数据类型的表现与实现 四、算法和算法分析 4.1 - 算法的定义及特性 4.2 - 评价…...

QIfw制作软件安装程序
前言 Qt Installer Framework是Qt默认包的发布框架。它很方便,使用静态编译Qt制作而成。从Qt的下载地址中下载Qt Installer Framework,地址是:http://download.qt.io/official_releases/qt-installer-framework/ 。支持我们自定义一些我们需要的东西包括页面、交互等。 框…...
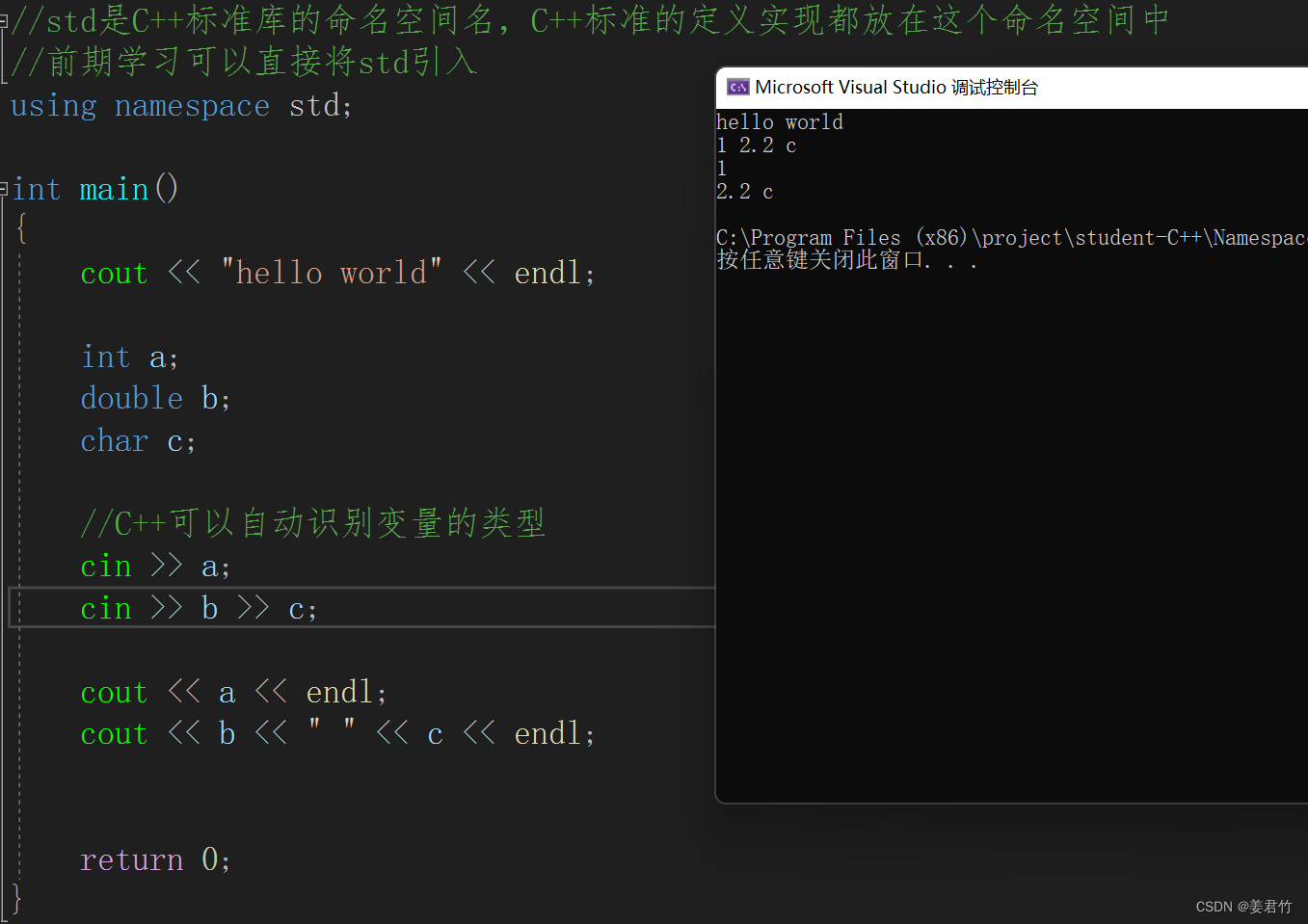
【C++】C++入门(上)
前言: C是在C语言的基础上不断添加东西形成的一门语言,在C语言的基础上引入了面向对象的思想。因此C既是面向对象的语言,也是面向过程的语言。因为C是以C语言为基础的,所以基本上C兼容所有的C语言。目前最常用的版本是C98和C11这两…...
)
5. Kimball维度建模常用术语及概念(一)
文章目录维度建模过程相关概念1. 收集业务需求与数据实现2. 协作维度建模研讨3. 四步骤维度设计过程4. 业务过程5. 粒度6. 描述环境的维度7. 用于度量的事实8. 维度模型事实表技术术语1. 事实表结构2. 可加、半可加、不可加事实3. 事实表中的空值4. 一致性事实5. 事务事实表6. …...

内核调试之Panic-Oops日志分析
这部分我们接着之前的思考,看看内核异常日志的分析。 1 Panic 调试 2 Oops调试 内核出现Panic或Oops错误,如何分析定位问题原因? 首先,保留现场,如下所示为一次非法虚拟地址访问错误。 EXT4-fs (sdc3): recovery c…...
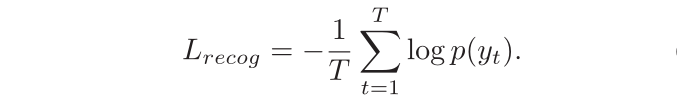
论文解读 | [AAAI2020] 你所需要的是边界:走向任意形状的文本定位
目录 1、研究背景 2、研究的目的 3、方法论 3.1 Boundary Point Detection Network(BPDN) 3.2 Recognition Network 3.3 Loss Functions 4、实验及结果 论文连接:https://ojs.aaai.org/index.php/AAAI/article/view/6896 1、研究背景 最近,旨在…...

数据挖掘流程简单示例10min
数据挖掘流程简单示例10min 套路: 准备数据实现算法测试算法 任务1:亲和性分析 如果一个顾客买了商品X,那么他们可能愿意买商品Y衡量方法: 支持度support : 所有买X的人数 置信度confidence : 所有买X和Y的人数所有买X的人数…...
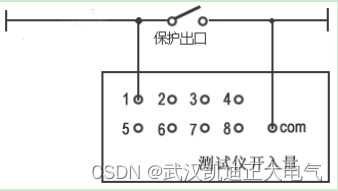
KDJB1200六相继电保护测试仪
一、概述 KDJB1200继电保护测试仪是在参照电力部颁发的《微机型继电保护试验装置技术条件(讨论稿)》的基础上,广泛听取用户意见,总结目前国内同类产品优缺点,充分使用现代新的的微电子技术和器件实现的一种新型小型化微机继电保护测试仪。可…...
从WEB到PWA 开发-发布-安装
见意如题!本文主要来说说PWA开发!作为一个前端程序员,在没有任何Android/IOS的开发情况下,想想我们有多少种方法来开发一个原生移动应用程序!我们可以有非原生、混合开发,PWA等等手段。类似uniappÿ…...

FPGA纯vhdl实现MIPI CSI2 RX视频解码输出,OV13850采集,提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...

《NFL橄榄球》:卡罗来纳黑豹·橄榄1号位
卡罗来纳黑豹(英语:Carolina Panthers)是一支位于北卡罗来纳州夏洛特的职业美式橄榄球球队。他们是国家美式橄榄球联合会的南区其中一支球队。他们与杰克逊维尔美洲虎在1995年加入NFL,成为扩充球队。 2018年球队市值为23亿美元&am…...
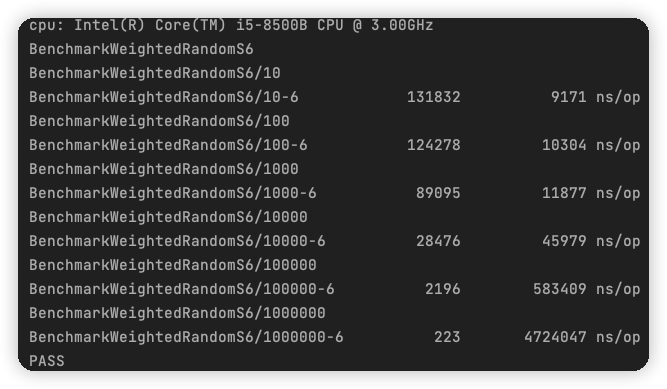
我说我为什么抽不到SSR,原来是这段代码在作祟...
本文是龚国玮所写,熊哥有所新增修改删减,原文见文末。 我说我为什么抽不到SSR,原来是加权随机算法在作祟 阅读本文需要做好心理准备,建议带着深究到底的决心和毅力进行学习! 灵魂拷问 为什么有 50% 的几率获得金币&a…...

MySQL MGR 集群新增节点
前言 服务器规划现状(CentOS7.x) IP地址主机名部署角色192.168.x.101mysql01mysql192.168.x.102mysql02mysql192.168.x.103mysql03mysql192.168.x.104proxysql01proxysql、keepalived192.168.x.105proxysql02proxysql、keepalived 新增服务器IP&#x…...

【单目标优化算法】蜣螂优化算法(Dung beetle optimizer,DBO)(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
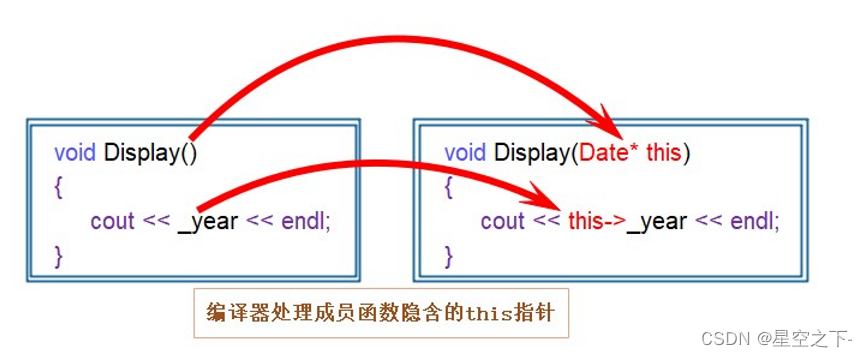
【C++】类和对象入门必知
面向过程和面向对象的初步认识类的引入类的定义类的访问限定符封装类的作用域类的实例化类对象模型this指针C语言和C实现Stack的对比面向过程和面向对象的初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解…...

day38 动态规划 | 509、斐波那契数 70、爬楼梯 746、使用最小花费爬楼梯
题目 509、斐波那契数 斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其…...

2023年备考软考必须知道的6件事
不知不觉,距离2023年上半年软考也只有不到100天的时间了,报名入口也将在3月13日正式开通,你是正在犹豫是否参加考试? 还是已经开始着手准备复习? 关于软考考试你还有哪些疑问? 2023年备考软考必须知道的6件事,建议收藏…...

GLOG如何控制输出的小数点位数
1 问题 在小白的蹩脚翻译演绎型博文《GLOG从入门到入门》中,有位热心读者提问说:在保存日志时,浮点型变量的小数位数如何设置? 首先感谢这位“嘻嘻哈哈的地球人”赏光阅读了小白这不太通顺的博客文章,并提出了一个很…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
