在 Ubuntu18.04 上编译安装 GMP
(2021.08.04)最近为了安装 IBM 的开源项目 HElib C++,需要在服务器上先安装GMP和NTL,NTL需要依赖GMP,所以先来安装一下GMP,记录一下在服务器上安装成功的过程:)
直接安装libgmp二进制文件
sudo apt-get install libgmp-dev
如果选择直接安装编译好的二进制文件,可以跳到看「检查是否安装成功」部分进行测试;如果想要编译安装,就接着往下看~
安装依赖
我的系统是Ubuntu 18.04 LTS,先安装一下GMP库的依赖:
sudo apt-get install m4
下载并解压GMP压缩文件
在GMP的官网1有.tar.lz,.tar.gz,.tar.zst版本的压缩文件,可以下载到本地再上传到服务器,也可以复制链接后直接在服务器上使用 wget/curl 下载(这边以gmp-6.2.1为例):
# 1. 使用 wget 下载 gmp-6.2.1.tar.xz
wget https://gmplib.org/download/gmp/gmp-6.2.1.tar.xz# 2. 或者使用 curl 下载 gmp-6.2.1.tar.xz
curl https://gmplib.org/download/gmp/gmp-6.2.1.tar.xz --output gmp-6.2.1.tar.xz
然后进行解压 2:
# 1. 对gmp-6.2.1.tar.xz进行解压
xz -d gmp-6.2.1.tar.xz && tar xvf gmp-6.2.1.tar# 2. 对gmp-6.2.1.tar.gz进行解压
tar -zxvf gmp-6.2.1.tar.gz# 3. 解压zst文件需要先安装zstd包,然后再对gmp-6.2.1.tar.zst进行解压
sudo apt install zstd
tar -I zstd -xvf gmp-6.2.1.tar.zst
然后就可以开始安装了~
编译安装GMP
# 进入gmp目录
cd gmp-6.2.1
# 设置安装路径前缀,建议设置为/usr
./configure --prefix=/usr --enable-cxx
# 开始编译安装
make
make check
sudo make install
检查是否安装成功
可以先进入 /usr/local/lib 目录查看有没有 libgmp 相关的文件。
cd /usr/local/lib
ls
# 大概会包含下面这些文件,基本上就说明安装成功了
# libgmp.a libgmp.so.10 libgmpxx.la libgmpxx.so.4.6.1
# libgmp.la libgmp.so.10.4.1 libgmpxx.so libgmpxx.so.4
# libgmp.so libgmpxx.a
然后再来编译一个简单的测试
# 使用vim编辑器新建并打开一个文件
vim testGMP.cpp
在vim打开的空文件中,切换为英文输入法,按i来进入插入模式,粘贴下面的代码,再按esc键退出插入模式,输入:wq然后回车,即可保存并退出。
#include <gmpxx.h>
#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{mpz_t a, b, c;mpz_init(a);mpz_init(b);mpz_init(c);printf("========= Input a and b => Output a + b =========\n");printf("[-] a = ");gmp_scanf("%Zd", a);printf("[-] b = ");gmp_scanf("%Zd", b);mpz_add(c, a, b);gmp_printf("[+] c = %Zd\n",c);return 0;
}
然后可以通过ls命令看到当前目录下面有testGMP.cpp这个文件,就可以对其进行编译测试了。
# 编译testGMP.cpp
g++ testGMP.cpp -o testGMP -lgmp -lm
# 没有报错的话就说明安装成功~运行即可
./testGMP
根据提示输入大整数a和b,到这里就说明测试成功了
========= Input a and b => Output a + b =========
[-] a = 11111111111111111111111111
[-] b = 22222222222222222222222222
[+] c = 33333333333333333333333333
如果这边文章对你有帮助的话,可以给这篇文章点一个赞👍
后面继续更新「编译安装NTL库」~
参考
https://gmplib.org ↩︎
tar.zst 文件格式解压 ↩︎
相关文章:

在 Ubuntu18.04 上编译安装 GMP
(2021.08.04)最近为了安装 IBM 的开源项目 HElib C,需要在服务器上先安装GMP和NTL,NTL需要依赖GMP,所以先来安装一下GMP,记录一下在服务器上安装成功的过程:) 直接安装libgmp二进制文…...
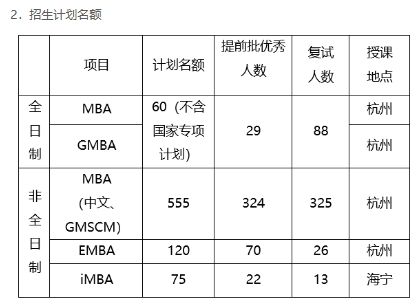
到底什么样的条件才能被浙大MBA录取?攻略集合
新一年管理类联考已悄然启动,很多考生把目标也都放在了浙江大学MBA项目上,那么浙江大学MBA项目好考吗?报考流程是怎样的?杭州达立易考教育在这里给大家汇总整理了浙大MBA项目相关资讯,分享给想要报考浙大MBA的同学&…...
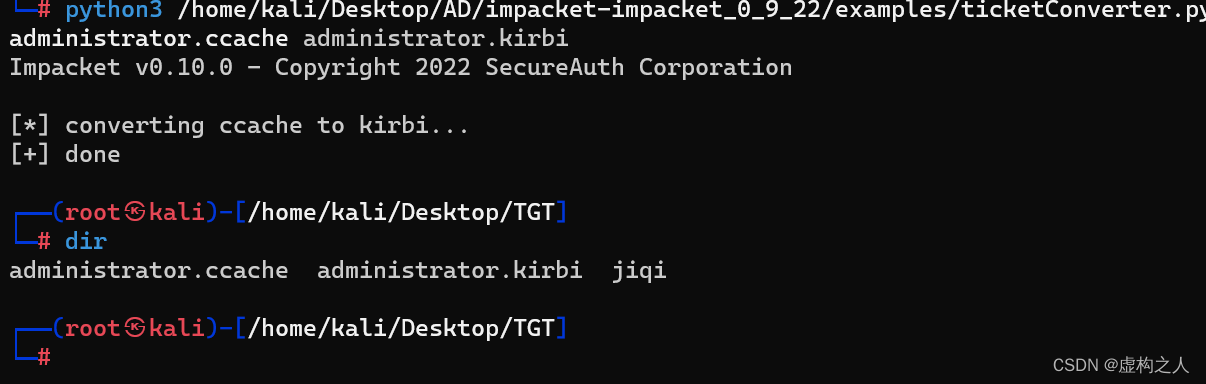
Impacket工具使用
Impacket工具说明 Impacker是用户处理网络协议的Python类集合,用于对SAB1-3或IPv4/IPv6 上的TCP/UPD/ICMP/IGMP/ARP/IPv4/IPv6/SMB/MSRPC/NTLM/Kerberos/WMI/LDAP 等进行低级的编程访问,数据包可以从头开始构建,也可以从原始数据包中解析, 面向对象API使用处理协议的深层结构变…...
)
华为OD机试真题Python实现【RSA 加密算法】真题+解题思路+代码(20222023)
RSA 加密算法 题目 RSA 加密算法在网络安全世界中无处不在 它利用了极大整数因数分解的困难度,数据越大安全系数越高 给定了一个32位正整数,请对其进行因数分解 找出哪两个素数的乘积 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输…...
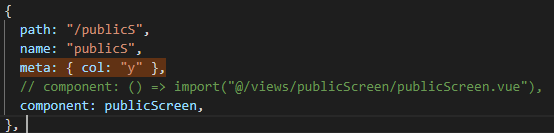
App.vue中读取不到路由的信息
问题: 首先定义了一个路由,并且在路由元里面存储了一个变量,在App.vue里面访问这个变量的时候却显示undefined!在路由对应的组件中却能访问到! 定义的路由元信息: 为啥访问不到…,懵逼的我在App.vue里…...

Lambda表达式详解
文章目录1、Lambda表达式简介2、如何使用Lambda表达式3、在哪里使用Lambda表达式3.1 函数式接口3.2函数描述符4、四大核心函数式接口4.1 Predicate4.2 Consumer4.3 Function4.4 Supplier5、方法引用5.1 方法引用的使用情况6、构造器引用7、数组引用8、复合Lambda表达式的有用方…...
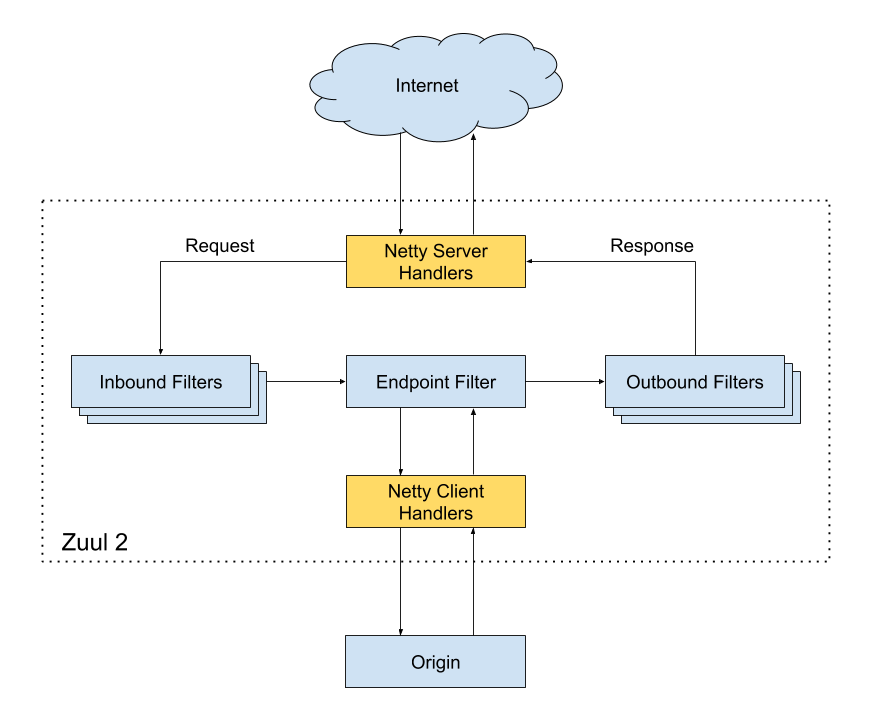
网关的通用设计框架
概念 网关,很多地方将网关比如成门, 没什么问题, 但是需要区分网关与网桥的区别。 网桥:工作在数据链路层,在不同或相同类型的LAN之间存储并转发数据帧,必要时进行链路层上的协议转换。可连接两个或多个网络…...
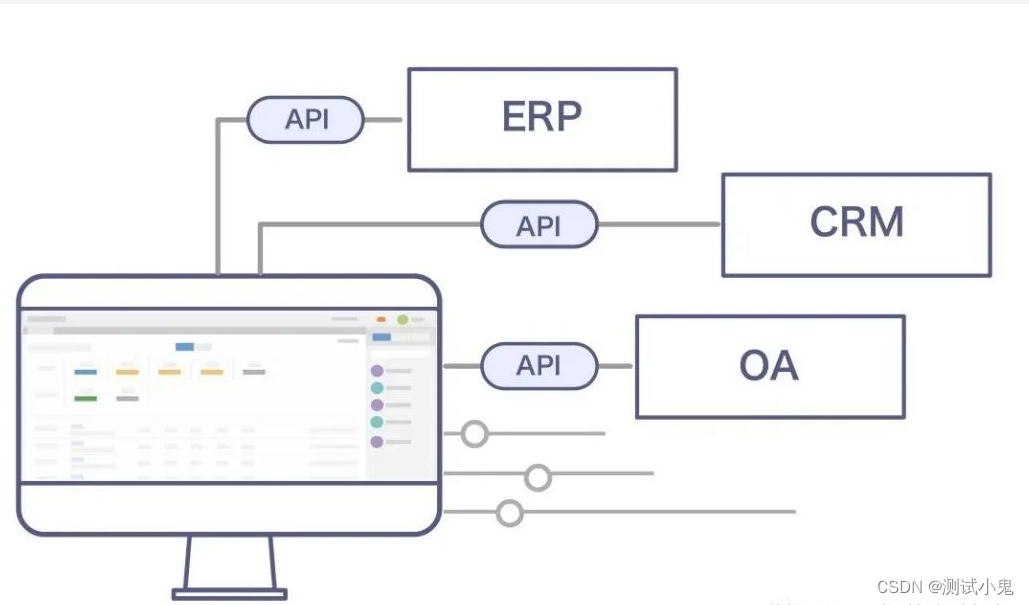
API 接口应该如何设计?如何保证安全?如何签名?如何防重?
说明:在实际的业务中,难免会跟第三方系统进行数据的交互与传递,那么如何保证数据在传输过程中的安全呢(防窃取)?除了https的协议之外,能不能加上通用的一套算法以及规范来保证传输的安全性呢&am…...

LeetCode-131. 分割回文串
目录题目思路回溯题目来源 131. 分割回文串 题目思路 切割问题类似组合问题。 例如对于字符串abcdef: 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…。切割问题:切割一个a之后&…...
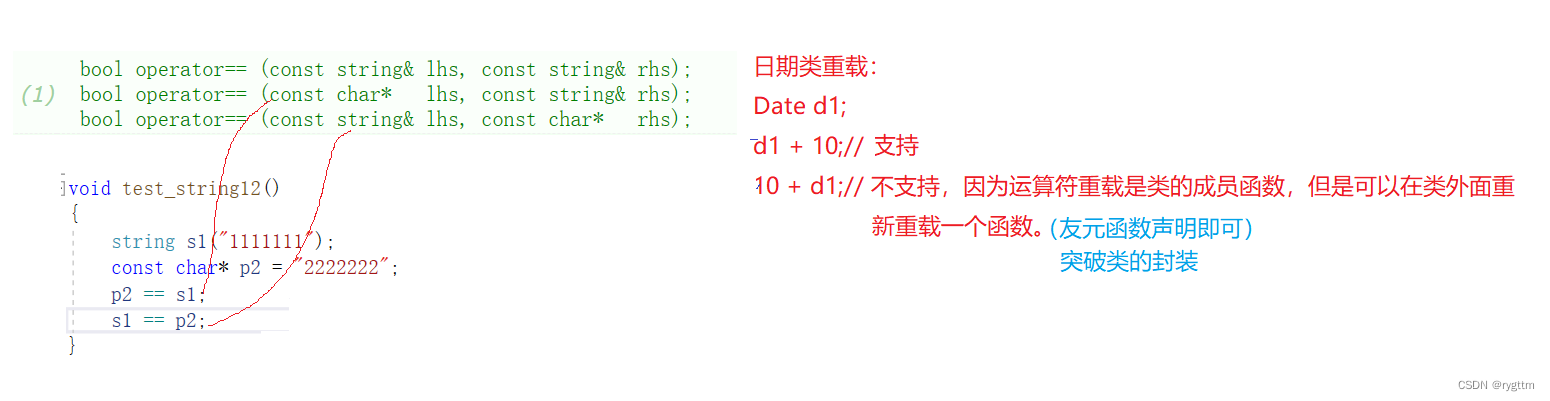
【C++】string类的基本使用
层楼终究误少年,自由早晚乱余生。你我山前没相见,山后别相逢… 文章目录一、编码(ascll、unicode字符集、常用的utf-8编码规则、GBK)1.详谈各种编码规则2.汉字在不同的编码规则中所占字节数二、string类的基本使用1.string类的本质…...
【第一章 - 绪论】- 数据结构(近八千字详解)
目录 一、 数据结构的研究内容 二、基本概念和术语 2.1 - 数据、数据元素、数据项和数据对象 2.2 - 数据结构 2.2.1 - 逻辑结构 2.2.2 - 存储结构 2.3 - 数据类型和抽象数据类型 三、抽象数据类型的表现与实现 四、算法和算法分析 4.1 - 算法的定义及特性 4.2 - 评价…...

QIfw制作软件安装程序
前言 Qt Installer Framework是Qt默认包的发布框架。它很方便,使用静态编译Qt制作而成。从Qt的下载地址中下载Qt Installer Framework,地址是:http://download.qt.io/official_releases/qt-installer-framework/ 。支持我们自定义一些我们需要的东西包括页面、交互等。 框…...
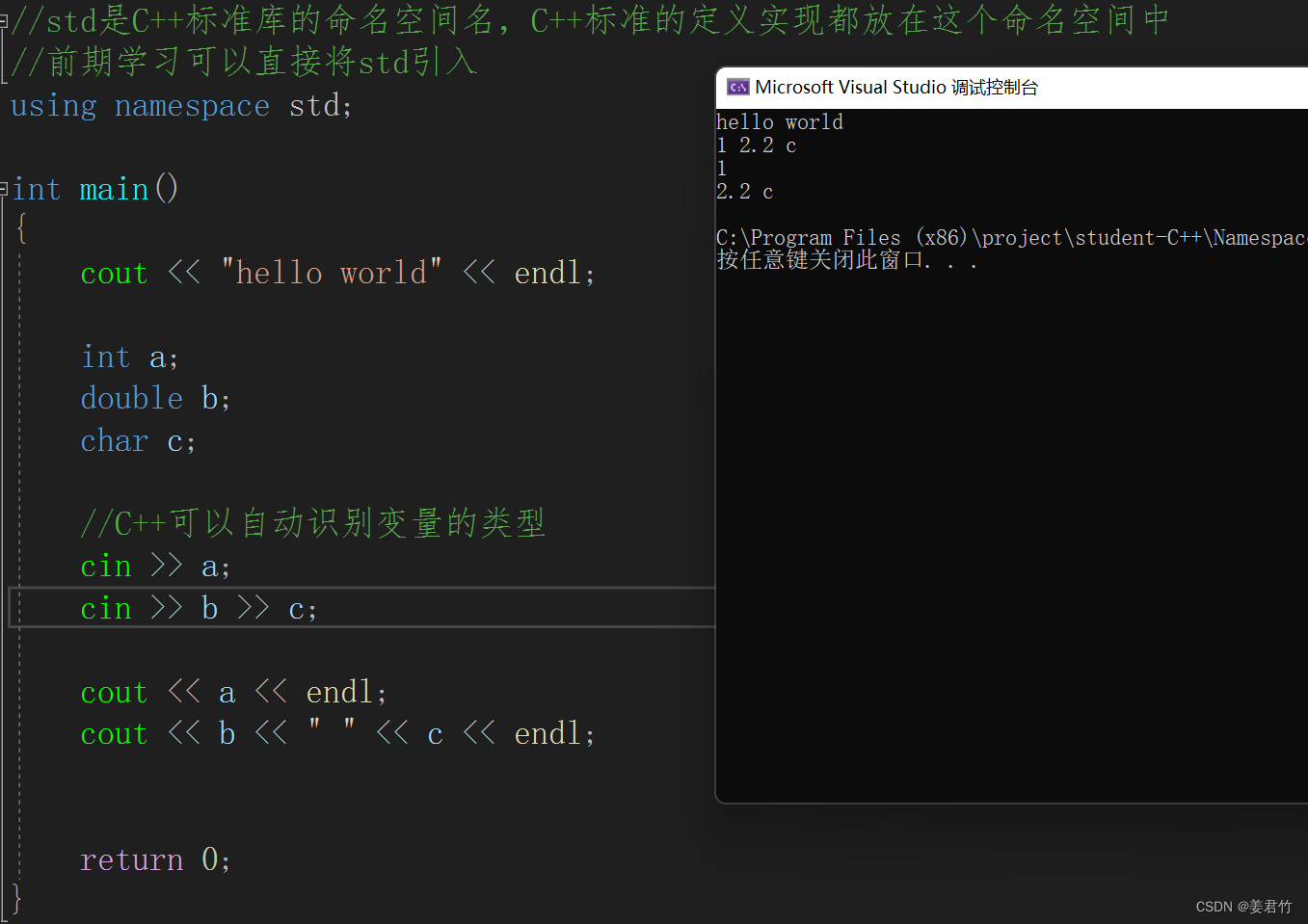
【C++】C++入门(上)
前言: C是在C语言的基础上不断添加东西形成的一门语言,在C语言的基础上引入了面向对象的思想。因此C既是面向对象的语言,也是面向过程的语言。因为C是以C语言为基础的,所以基本上C兼容所有的C语言。目前最常用的版本是C98和C11这两…...
)
5. Kimball维度建模常用术语及概念(一)
文章目录维度建模过程相关概念1. 收集业务需求与数据实现2. 协作维度建模研讨3. 四步骤维度设计过程4. 业务过程5. 粒度6. 描述环境的维度7. 用于度量的事实8. 维度模型事实表技术术语1. 事实表结构2. 可加、半可加、不可加事实3. 事实表中的空值4. 一致性事实5. 事务事实表6. …...

内核调试之Panic-Oops日志分析
这部分我们接着之前的思考,看看内核异常日志的分析。 1 Panic 调试 2 Oops调试 内核出现Panic或Oops错误,如何分析定位问题原因? 首先,保留现场,如下所示为一次非法虚拟地址访问错误。 EXT4-fs (sdc3): recovery c…...
论文解读 | [AAAI2020] 你所需要的是边界:走向任意形状的文本定位
目录 1、研究背景 2、研究的目的 3、方法论 3.1 Boundary Point Detection Network(BPDN) 3.2 Recognition Network 3.3 Loss Functions 4、实验及结果 论文连接:https://ojs.aaai.org/index.php/AAAI/article/view/6896 1、研究背景 最近,旨在…...

数据挖掘流程简单示例10min
数据挖掘流程简单示例10min 套路: 准备数据实现算法测试算法 任务1:亲和性分析 如果一个顾客买了商品X,那么他们可能愿意买商品Y衡量方法: 支持度support : 所有买X的人数 置信度confidence : 所有买X和Y的人数所有买X的人数…...
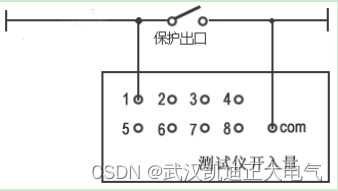
KDJB1200六相继电保护测试仪
一、概述 KDJB1200继电保护测试仪是在参照电力部颁发的《微机型继电保护试验装置技术条件(讨论稿)》的基础上,广泛听取用户意见,总结目前国内同类产品优缺点,充分使用现代新的的微电子技术和器件实现的一种新型小型化微机继电保护测试仪。可…...
从WEB到PWA 开发-发布-安装
见意如题!本文主要来说说PWA开发!作为一个前端程序员,在没有任何Android/IOS的开发情况下,想想我们有多少种方法来开发一个原生移动应用程序!我们可以有非原生、混合开发,PWA等等手段。类似uniappÿ…...

FPGA纯vhdl实现MIPI CSI2 RX视频解码输出,OV13850采集,提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
