当前位置： 首页 > news >正文

Fast-DDS 服务发现简要概述

news 2026/2/9 15:01:42

阅读本文章需要对DDS基础概念有一些了解，一些内容来自Fast-DDS官方文档，一些是工作中踩过的坑。

1. 服务发现阶段

满足OMG标准的DDS服务发现分为两部分，分别是:

  • PDP(Participant Discovery Protocol 参与者发现协议)：参与者确认彼此的存在。参与者会定期发送公告信息，消息包括但不限于参与者的名称，ID，所在进程信息，所在主机信息，以及监听用户数据以及发现数据的IP Port等；
  • EDP(Endpoint Discovery Protocol 端点发现协议)。确认 DataWriter 和 DataReader 的信息，如Topic,数据类型等信息

PDP和EDP不同DDS可以有不同的实现方式，为了使得不同厂家的DDS能够互相通信，OMG标准规定，所有种类的DDS都需要实现SPDP和SEDP，即简单参与者发现协议和简单端点发现协议，以满足互操性。

Fast DDS提供的服务发现机制

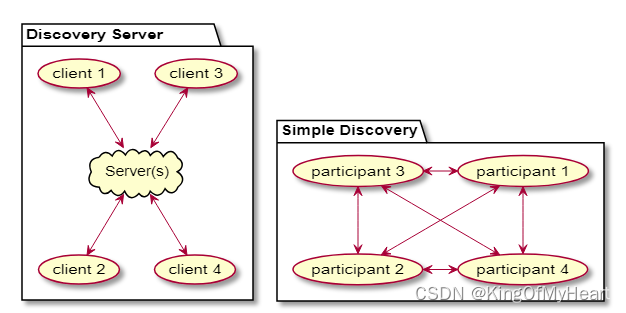
  1. 简单发现：及上述的SPDP和SEDP协议，保证了Fast-DDS和其余品种的DDS的互操性，兼容性；

  2. 静态发现：在PDP阶段使用的是SPDP。但是可以在EDP阶段，在配置文件中指定要进行交互的端点(datawriter/datareader)的一些信息，如Topic，数据类型，通信的IP和端口号等。

  3. 发现服务器：基于C/S结构，发现消息等元流量由一个或者多个充当服务器的参与者进行管理。
    在这里插入图片描述

  4. 手动发现：不与DDS层兼容，与底层RTPS层兼容。该机制禁用PDP，需要用户手动的匹配RTPSParticipants,RTPSReaders和RTPSWriters，用户将需要使用外部的元信息交换的通信机制。

相关文章：

Fast-DDS 服务发现简要概述

阅读本文章需要对DDS基础概念有一些了解，一些内容来自Fast-DDS官方文档，一些是工作中踩过的坑。 1. 服务发现阶段 满足OMG标准的DDS服务发现分为两部分，分别是: PDP(Participant Discovery Protocol 参与者发现协议)：参与者确认…...

编程日记 2023/9/12 23:50:22

基于spingboot的websocket订阅、广播、多人聊天室示例

概述 基于spingboot的websocket多人聊天系统。包括订阅，广播、点对点单人聊天，多人聊天室功能。 详细 一、运行效果 简单示例 广播 单人聊天 多人聊天室 二、相关代码 websocket配置 package com.iamgpj.demowebsocket.config;import com.iamgpj.d…...

编程日记 2023/9/12 23:48:19

Linux mac Windows三系统 局域网文件共享方法

主要工具： Samba是一个开源的软件套件，允许Linux系统与Windows系统之间共享文件和打印机。 一、首先是Linux共享的设置 ①安装 sudo apt-get install samba ②创建共享文件夹 sudo mkdir /home/share ③配置用户 sudo smbpasswd -a kequan ④修改…...

编程日记 2023/9/12 23:47:18

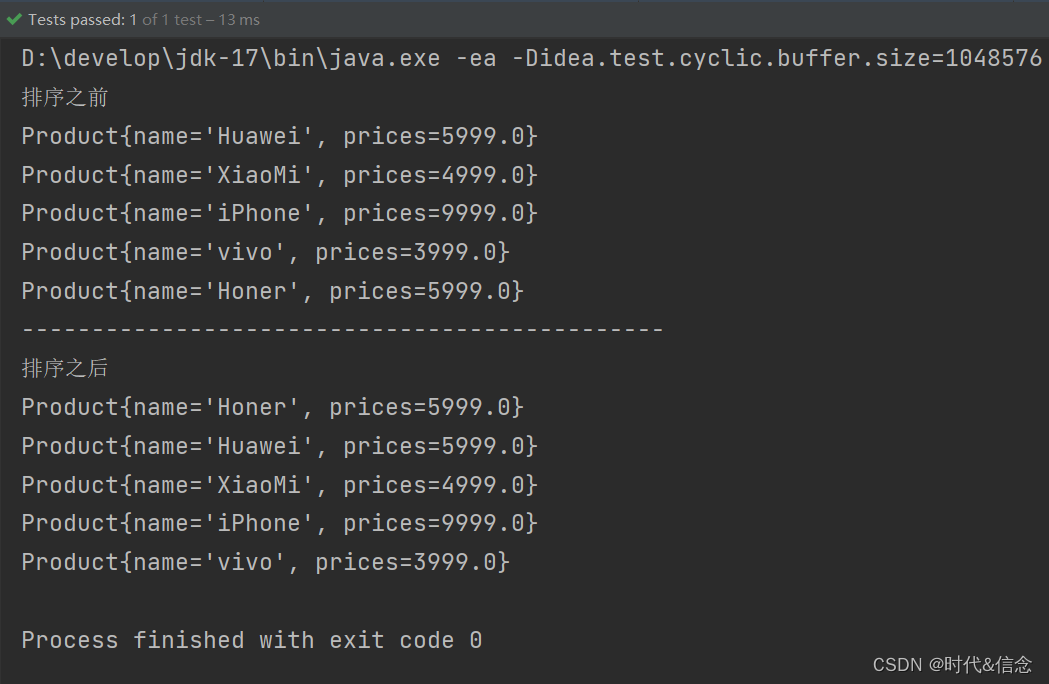
Java——比较器

引入的背景 我们知道基本数据类型的数据（除boolean类型外）需要比较大小的话，直接使用比较运算符即可，但是引用数据类型是不能直接使用比较运算符来比较大小的。那么，如何解决这个问题呢？ 在Java中经常会涉…...

编程日记 2023/9/12 23:46:17

【数据结构】初识泛型

文章目录 一般的类和方法，只能使用具体的类型: 要么是基本类型，要么是自定义的类。这种限制对代码的束缚就会很大。所以我们引入了泛型。泛型，泛顾名思义就是广泛的意思。就是适用于许多许多类型。从代码上讲，就是对类型实现了参数…...

编程日记 2023/9/12 23:45:16

代码随想录--哈希--有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。 示例 1: 输入: s "anagram", t "nagaram" 输出: true 示例 2: 输入: s "rat", t "car" 输出: false 说明: 你可以假设字符串只包含小写字母。…...

编程日记 2023/9/12 23:44:15

MySQL——数据的增删改

2023.9.12 本章开始学习DML (数据操纵语言) 语言。相关学习笔记如下： #DML语言 /* 数据操作语言： 插入：insert 修改：update 删除：delete */#一、插入语句 #方式一：经典的插入 /* 语法： insert …...

编程日记 2023/9/12 23:43:14

云服务器与http服务器

如何与http服务器建立连接（客户端）？ http请求设计格式： 例子： 发送http请求 http数据响应格式： 接收http服务器返回的数据需要进一步进行字符串处理操作，提取有用的数据。...

编程日记 2023/9/12 23:41:12

golang教程 beego框架笔记一

安装beego 安装bee工具 beego文档 # windos 推荐使用 go install github.com/beego/bee/v2master go get -u github.com/beego/bee/v2masterwindows使用安装bee工具时碰到的问题； 环境配置都没有问题，但是执行官网的命令：go get -u github…...

编程日记 2023/9/12 23:40:10

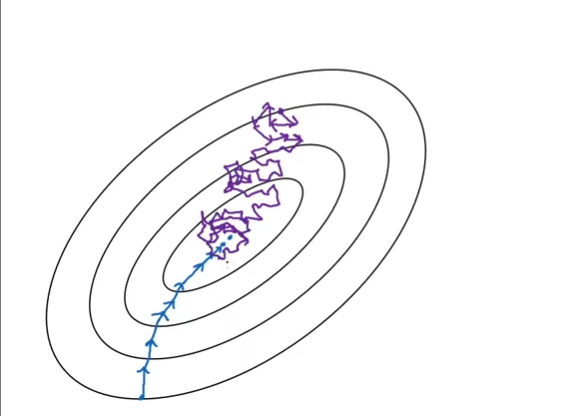
【深度学习】Mini-Batch梯度下降法

Mini-Batch梯度下降法 在开始Mini-Batch算法开始之前，请确保你已经掌握梯度下降的最优化算法。 在训练神经网络时，使用向量化是加速训练速度的一个重要手段，它可以避免使用显式的for循环，并且调用经过大量优化的矩阵计算函数库。…...

编程日记 2023/9/12 23:38:07

AI项目六：WEB端部署YOLOv5

若该文为原创文章，转载请注明原文出处。 一、介绍 最近接触网页大屏，所以就想把YOLOV5部署到WEB端，通过了解，知道了两个方法： 1、基于Flask部署YOLOv5目标检测模型。 2、基于Streamlit部署YOLOv5目标检测。 代码在…...

编程日记 2023/9/12 23:36:05

敲代码常用快捷键

1、代码拖动 PyCharm：按住 shiftalt鼠标选中某一区域来拖动，即可实现拖动这一区域至指定区域。Visual Studio Code (VSCode): - Windows/Linux：Alt 鼠标左键拖动 - MacOS：Option 鼠标左键拖动 IntelliJ IDEA: - Win…...

编程日记 2023/9/12 23:34:03

MyBatis: 分页插件PageHelper直接传递分页参数的用法

一、加分页插件依赖 <dependency><groupId>com.github.pagehelper</groupId><artifactId>pagehelper-spring-boot-starter</artifactId><version>1.2.13</version></dependency>二、配置分页插件&#xff0c;并配置相关属性&a…...

编程日记 2023/9/12 23:32:01

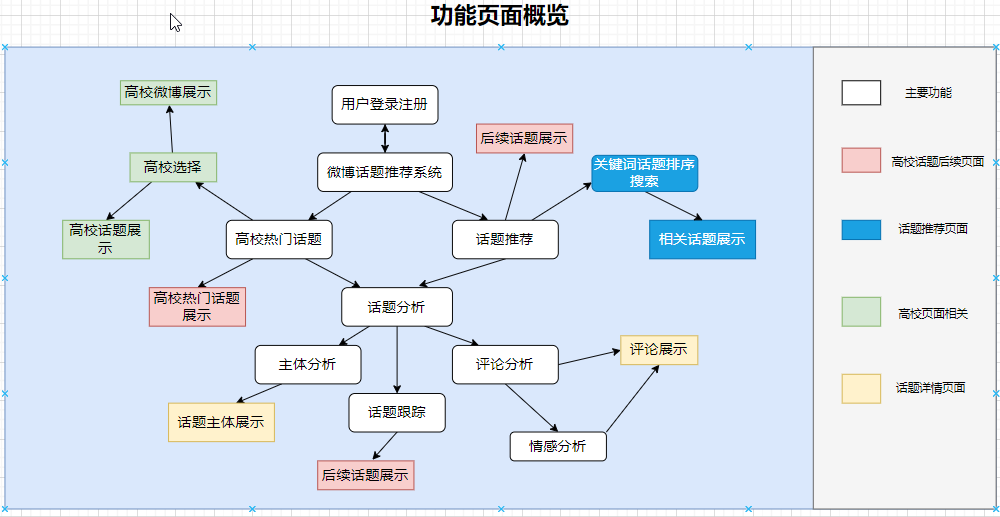
Python基于Flask的高校舆情分析，舆情监控可视化系统

博主介绍&#xff1a;✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 运行效果图 基于Python的微博大数据舆情分析&#xff0c;舆论情感分析可视化系统 系统介绍 微博舆情分析系…...

编程日记 2023/9/12 23:31:00

Python第一次作业练习

题目分析&#xff1a; """ 参考学校的相关规定。 对于四分制&#xff0c;百分制中的90分及以上可视为绩点中的4分&#xff0c;80 分及以上为3分&#xff0c;70 分以上为2分&#xff0c;60 分以上为1分; 五分制中的5分为四分制中的4分&#xff0c;4分为3分&#…...

编程日记 2023/9/12 23:29:59

InstallShield打包升级时不覆盖原有文件的解决方案

一个.NET Framework的Devexpress UI Windows Form项目&#xff0c;用的InstallShield&#xff0c;前些个版本都好好的&#xff0c;最近几个版本突然就没法更新了&#xff0c;每次更新的时候都覆盖不了原文件&#xff0c;而且这样更新后第一次打开程序&#xff08;虽然是老程序&…...

编程日记 2023/9/12 23:28:58

服务器巡检表-监控指标

1、巡检指标 系统资源K8S集群NginxJAVA应用RabbitMQRedisPostgreSQLElasticsearchELK日志系统 2、巡检项 检查项目 检查指标 检查标准 系统资源 CPU 使用率 正常&#xff1a;&#xff1c;70% 低风险&#xff1a;≥ 70% 中风险&#xff1a;≥ 85% 高风险&#xff1a;≥ 9…...

编程日记 2023/9/12 23:22:52

无涯教程-JavaScript - DDB函数

描述 DDB函数使用双倍余额递减法或您指定的某些其他方法返回指定期间内资产的折旧。 语法 DDB (cost, salvage, life, period, [factor])争论 Argument描述Required/OptionalCostThe initial cost of the asset.RequiredSalvage 折旧结束时的价值(有时称为资产的残值)。 该…...

编程日记 2023/9/12 23:18:48

uniapp打包微信小程序。报错：https://api.weixin.qq.com 不在以下 request 合法域名列表

场景&#xff1a;在进行打包上传测试时&#xff0c;发现登录失效&#xff0c;但在测试中【勾选不效应合法域名】就可以。 出现原因&#xff1a;我在获取到用户code后&#xff0c;直接使用调用官方接口换取openid 解决方案&#xff1a; 可以把code带给后端&#xff0c;让他们返…...

编程日记 2023/9/12 23:14:42

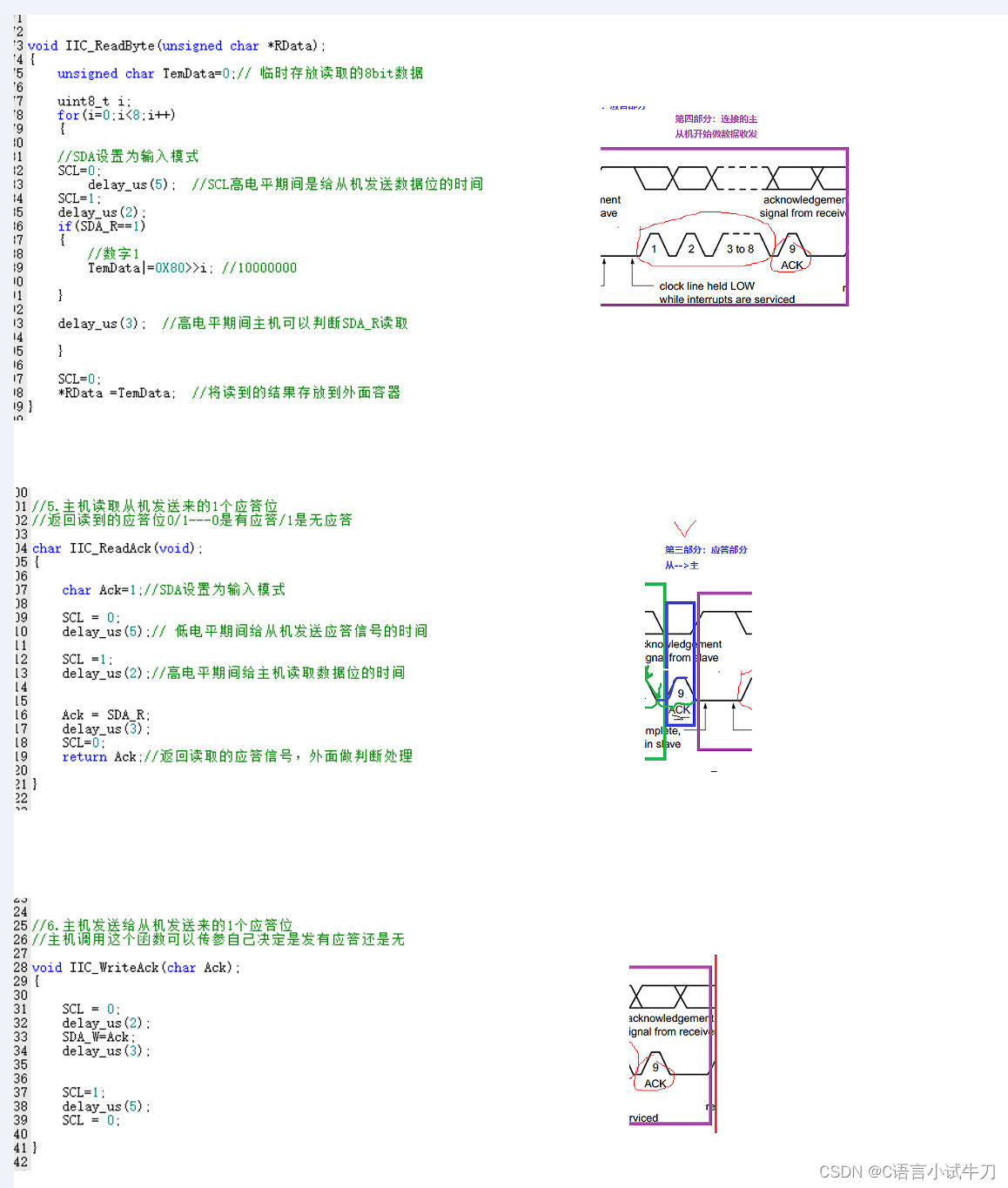
stm32之31.iic

iic双线制。一根是SCL&#xff0c;作为时钟同步线;一根是SDA&#xff0c;作为数据传输线 SDN #include "iic.h"#define SCL PBout(8)#define SDA_W PBout(9) #define SDA_R PBin(9)void IIC_GPIOInit(void) {GPIO_InitTypeDef GPIO_InitStructure;//使能时钟GR…...

编程日记 2023/9/12 23:12:41

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例

使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件&#xff0c;常用于在两个集合之间进行数据转移&#xff0c;如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model&#xff1a;绑定右侧列表的值&…...

编程新知 2026/2/4 4:25:40

Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务

通过akshare库&#xff0c;获取股票数据&#xff0c;并生成TabPFN这个模型 可以识别、处理的格式&#xff0c;写一个完整的预处理示例&#xff0c;并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务&#xff0c;进行预测并输…...

编程新知 2025/9/20 4:34:47

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候&#xff0c;写过一篇简单实现&#xff0c;后期随着对该模型的深入研究&#xff0c;本次记录涉及到prophet 的公式以及参数调优&#xff0c;从公式可以更直观…...

编程新知 2026/1/27 5:01:54

新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案

随着新能源汽车的快速普及&#xff0c;充电桩作为核心配套设施&#xff0c;其安全性与可靠性备受关注。然而&#xff0c;在高温、高负荷运行环境下&#xff0c;充电桩的散热问题与消防安全隐患日益凸显&#xff0c;成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

编程新知 2026/1/29 3:00:56

CMake 从 GitHub 下载第三方库并使用

有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...

编程新知 2026/2/1 3:19:54

怎么让Comfyui导出的图像不包含工作流信息，

为了数据安全&#xff0c;让Comfyui导出的图像不包含工作流信息&#xff0c;导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo&#xff08;推荐&#xff09;​​ 在 save_images 方法中&#xff0c;​​删除或注释掉所有与 metadata …...

编程新知 2025/8/13 15:12:54

C语言中提供的第三方库之哈希表实现

一. 简介 前面一篇文章简单学习了C语言中第三方库&#xff08;uthash库&#xff09;提供对哈希表的操作&#xff0c;文章如下&#xff1a; C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

编程新知 2025/11/9 14:40:17

Java求职者面试指南：Spring、Spring Boot、Spring MVC与MyBatis技术解析

Java求职者面试指南&#xff1a;Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么&#xff1f;它的作用是什么&#xff1f; Spring框架的核心容器是IoC&#xff08;控制反转&#xff09;容器。它的主要作用是管理对…...

编程新知 2025/7/17 8:16:30

Neko虚拟浏览器远程协作方案：Docker+内网穿透技术部署实践

前言&#xff1a;本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中&#xff0c;跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南&#xff0c;你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案&#xff0c;并结合内网…...

编程新知 2026/1/27 9:02:37

链式法则中 复合函数的推导路径 多变量“信息传递路径”

非常好&#xff0c;我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题&#xff0c;统一使用 二重复合函数&#xff1a; z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y))​ 来全面说明。我们会展示其全微分形式&#xff08;偏导…...

编程新知 2026/2/8 12:07:50