【随想】每日两题Day.3(实则一题)
题目:59.螺旋矩阵||
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
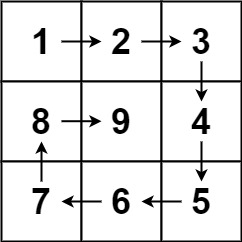
输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
代码:
class Solution {public int[][] generateMatrix(int n) {int[][] arr = new int[n][n];int start = 0;//控制起始位置int offset = 1;//控制终止位置int loop = 0;//控制循环次数int count = 1;int i,j;while(loop++<n/2) {for(j = start;j < n-offset;j++) {arr[start][j] = count++;}for(i = start;i < n-offset;i++) {arr[i][j] = count++;}for(;j>start;j--) {arr[i][j] = count++;}for(;i>start;i--) {arr[i][j] = count++;}start++;offset++;}if(n%2==1) {//如果n为奇数,那么最后处理中间arr[start][start] = count;}return arr;}
}思考:
这道题我看了很久,写了错,错了改,改了错...后来乱了。看了题解之后明白,循环要采取一个方式左闭右开。然后start控制他的起始位置,offset控制他的终止位置。每圈循环完毕后,要start++,offset++。要注意的是while循环的条件是要循环的圈数也就是n/2,当最后循环完后,我们要单独处理奇数n的中心的值,也就是arr[start][start]的值。就是这样。
相关文章:

【随想】每日两题Day.3(实则一题)
题目:59.螺旋矩阵|| 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。 示例 1: 输入:n 3 输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2: …...

阿里后端开发:抽象建模经典案例【文末送书】
文章目录 写作前面1.抽象思维2.软件世界中的抽象3. 经典抽象案例4. 抽象并非一蹴而就!需要不断假设、验证、完善5. 推荐一本书 写作末尾 写作前面 在互联网行业,软件工程师面对的产品需求大都是以具象的现实世界事物概念来描述的,遵循的是人…...
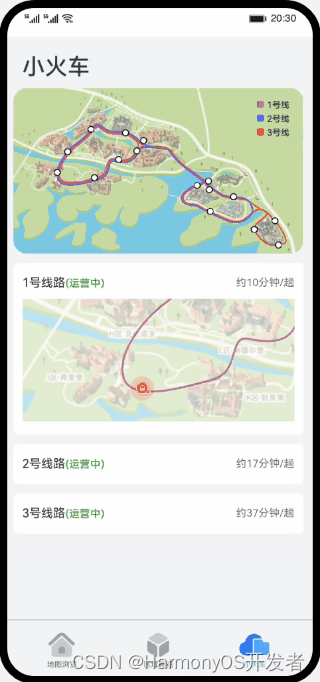
HarmonyOS Codelab 优秀样例——溪村小镇(ArkTS)
一、介绍 溪村小镇是一款展示溪流背坡村园区风貌的应用,包括园区内的导航功能,小火车行车状态查看,以及各区域的风景展览介绍,主要用于展示HarmonyOS的ArkUI能力和动画效果。具体包括如下功能: 打开应用时进入启动页&a…...

Mybatis---第二篇
系列文章目录 文章目录 系列文章目录一、#{}和${}的区别是什么?二、简述 Mybatis 的插件运行原理,如何编写一个插件一、#{}和${}的区别是什么? #{}是预编译处理、是占位符, KaTeX parse error: Expected EOF, got # at position 27: …接符。 Mybatis 在处理#̲{}时,会将…...
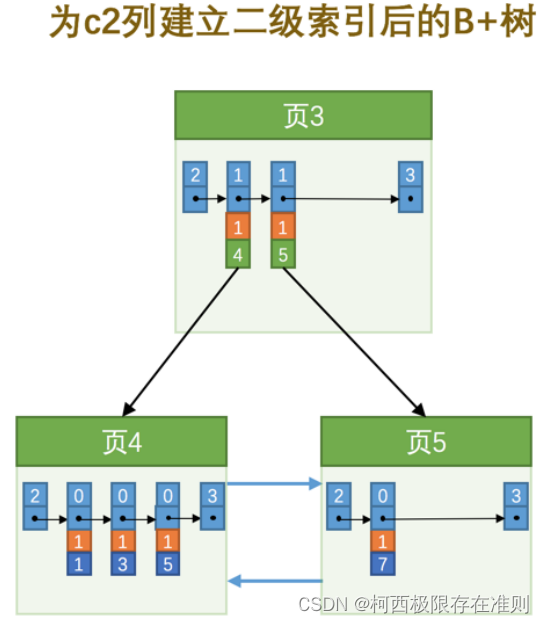
6.2.3 【MySQL】InnoDB的B+树索引的注意事项
6.2.3.1 根页面万年不动窝 B 树的形成过程是这样的: 每当为某个表创建一个 B 树索引(聚簇索引不是人为创建的,默认就有)的时候,都会为这个索引创建一个 根节点 页面。最开始表中没有数据的时候,每个 B 树…...
)
前端面试话术集锦第 12 篇:高频考点(Vue常考基础知识点)
这是记录前端面试的话术集锦第十二篇博文——高频考点(Vue常考基础知识点),我会不断更新该博文。❗❗❗ 这一章节我们将来学习Vue的一些经常考到的基础知识点。 1. 生命周期钩子函数 在beforeCreate钩子函数调用的时候,是获取不到props或者data中的数据的,因为这些数据的…...

骨传导耳机危害有哪些?值得入手吗?
事实上,只要是正常使用,骨传导耳机并不会对身体造成伤害,并且在众多耳机种类中,骨传导耳机可以说是相对健康的一种耳机,这种耳机最独特的地方便是声波不经过外耳道和鼓膜, 而是直接将人体骨骼结构作为传声介…...

网络爬虫-----初识爬虫
目录 1. 什么是爬虫? 1.1 初识网络爬虫 1.1.1 百度新闻案例说明 1.1.2 网站排名(访问权重pv) 2. 爬虫的领域(为什么学习爬虫 ?) 2.1 数据的来源 2.2 爬虫等于黑客吗? 2.3 大数据和爬虫又有啥关系&…...

vue 功能:点击增加一项,点击减少一项
功能介绍: 默认为一列,当点击右侧"" 号,增加一列;点击 “-” 号,将当前列删除; 功能截图: 功能代码: //HTML <el-col :span"24"><el-form-item lab…...

我的编程学习笔记
1. 引言: 在开始编写任何代码之前,都需要理解编程的基本概念。编程是人与计算机进行交流的方式,它让计算机可以理解和执行特定的任务。编程语言是这种交流的工具,而学习编程就是学习如何用特定的语言表达出我们想要的计算机行为。…...

页面静态化、Freemarker入门
页面静态化介绍 页面的访问量比较大时,就会对数据库造成了很大的访问压力,并且数据库中的数据变化频率并不高。 那需要通过什么方法为数据库减压并提高系统运行性能呢?答案就是页面静态化。页面静态化其实就是将原来的动态网页(例如通过ajax…...

PCL (再探)点云配准精度评价指标——均方根误差
目录 一、算法原理二、代码实现三、代码解析四、备注本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 见: 点云配准精度评价指标——均方根误差PCL 点云配准精度评价——点到面的均方根误差Open3D(C++) 点…...

【Redis速通】基础知识1 - 虚拟机配置与踩坑
Ubuntu 配置 Redis 下载 redis 找到 redis 官网界面,下载 redis6.2LTS 点击前往 用 mobax 连接到 ubuntu 虚拟机,把下载好的 tar.gz 文件丢到任意一个文件夹下面 进入该文件夹,于此处打开终端,进行解压操作:tar -z…...
我的创作纪念日---从考研调剂到研一的旅程
文章目录 一、前言二、机缘三、收获四、日常五、憧憬 一、前言 大家好,我是小馒头学Python,小馒头学Python就是我,今天是我第一次收到创作纪念日的私信,去年的今天我还在考研,那个时候整天浑浑噩噩的,迷茫…...

Python-实现邮件发送:flask框架或django框架可以直接使用
在项目中,会使用到发送邮件的功能。不同框架的配置可能有所不同,直接写一个不依赖框架配置的邮件发送模块。 使用的功能: 1、可以发送给多个邮箱 2、可以实现抄送多个邮箱 3、可以添加多个文件附件 一、不使用多线程 import smtplib from…...

使用亚马逊云科技Amazon SageMaker,为营销活动制作广告素材
广告公司可以使用生成式人工智能和文字转图像根基模型,制作创新的广告素材和内容。在本篇文案中,将演示如何使用亚马逊云科技Amazon SageMaker从现有的基本图像生成新图像,这是一项完全托管式服务,用于大规模构建、训练和部署机器…...

conda环境安装opencv带cuda版本
主要是cmake编译选项需要修改 以下两个选项按照自己情况修改 -D OPENCV_EXTRA_MODULES_PATH../opencv_contrib/modules \ -D CUDA_TOOLKIT_ROOT_DIR/usr/local/cuda-12.2 \ 其中/home/lixin/anaconda3/envs/stereo 改成你自己的conda环境 cmake -D CMAKE_BUILD_TYPER…...

R语言中的数据结构----矩阵
目录 (1)创建矩阵 (2) 线性代数运算 (3)矩阵索引 (4)矩阵元素的筛选 (5)增加或删除矩阵的行或列 (6)apply()函数 (…...
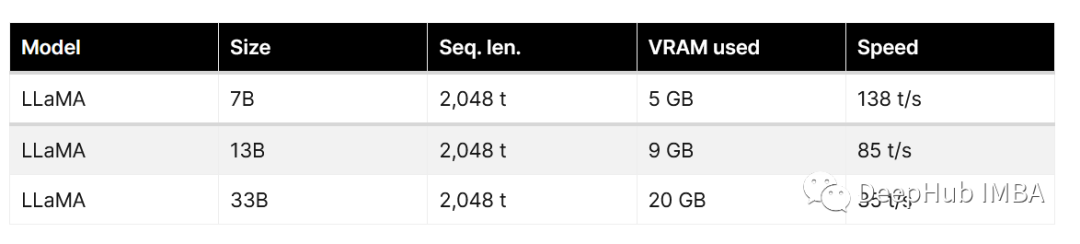
Llama-2 推理和微调的硬件要求总结:RTX 3080 就可以微调最小模型
大语言模型微调是指对已经预训练的大型语言模型(例如Llama-2,Falcon等)进行额外的训练,以使其适应特定任务或领域的需求。微调通常需要大量的计算资源,但是通过量化和Lora等方法,我们也可以在消费级的GPU上…...

C++多线程的用法(包含线程池小项目)
一些小tips: 编译命令如下: g 7.thread_pool.cpp -lpthread 查看运行时间: time ./a.out 获得本进程的进程id: this_thread::get_id() 需要引入的库函数有: #include<thread> // 引入线程库 #include<mutex> //…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
