逆市而行:如何在市场恐慌时保持冷静并抓住机会?
市场中的恐慌和波动是投资者所不可避免的。当市场出现恐慌情绪时,很多投资者会盲目跟从大众,导致决策出现错误。然而,聪明的投资者懂得在恐慌中保持冷静,并将其视为抓住机会的时机。本文将分享一些在市场恐慌时保持冷静并抓住机会的有效策略。
首先,了解市场背后的基本面。市场恐慌通常是由一系列负面事件引发的,例如经济衰退、自然灾害或政治不稳定。了解这些基本面的变化,能够帮助你更好地理解市场以及投资机会的变动。研究相关的新闻和数据,跟踪全球经济和金融动态,以便更好地掌握市场的走势。
其次,设定明确的投资目标和策略。在市场恐慌时,很容易受到情绪的影响而进行冲动的投资决策。为了避免这种情况,有一个明确的投资目标和策略非常重要。根据自己的风险承受能力和投资期限,制定合适的投资计划。并且要时刻关注自己的投资目标,不受短期市场波动的影响。
第三,分散投资组合。市场恐慌往往导致整个市场的下跌,因此资产的风险集中在特定的行业或公司上。为了降低风险,分散投资组合是关键。将投资分散到不同的行业、公司和地区,可以减少受到单一投资的影响,并增加长期收益的可能性。
第四,保持足够的储备资金。市场恐慌时,投资者常常表现出恐慌性的卖出行为,导致股价大幅下跌。此时,如果你有足够的储备资金,就可以抓住低估的投资机会。保持足够的现金储备,可以让你在低点时买入优质资产,享受未来上涨时的回报。
第五,学会控制情绪。市场恐慌时,投资者的情绪往往无法控制,从而引发冲动的投资决策。然而,冷静思考和理性决策才是成功投资的关键。学会控制情绪,可以避免盲目跟从市场情绪,并作出更明智的投资决策。
最后,与专业人士交流和学习。市场恐慌时,经验丰富的投资专家通常会有更好的判断和见解。与他们交流并学习他们的经验,可以帮助你更好地理解和应对市场的波动。参加相关的投资论坛、读书、参加培训课程等,不断学习和提升自己的投资知识和技巧。
通过了解市场基本面、设定明确的投资目标、分散投资组合、保持足够的储备资金、控制情绪以及与专业人士交流和学习,你就能够更好地应对市场恐慌,并找到投资机会。记住,市场恐慌并非终点,而是抓住机会的起点。
相关文章:

逆市而行:如何在市场恐慌时保持冷静并抓住机会?
市场中的恐慌和波动是投资者所不可避免的。当市场出现恐慌情绪时,很多投资者会盲目跟从大众,导致决策出现错误。然而,聪明的投资者懂得在恐慌中保持冷静,并将其视为抓住机会的时机。本文将分享一些在市场恐慌时保持冷静并抓住机会…...

SpringBoot项目在Linux上启动、停止脚本
文章目录 SpringBoot项目在Linux上启动、停止脚本1. 在项目jar包同一目录,创建脚本xxx.sh【注: 和项目Jar同一目录】2. xxx.sh脚本内容,实际项目使用,只需修改jar包的名称:xxxxxx.jar3. 给xxx.sh赋予执行权限4. xxx.sh脚本的使用 …...

基于32位单片机的感应灯解决方案
感应灯是一种常见照明灯,提起感应灯,相信大家并不陌生, 它在一些公共场所、卫生间或者走廊等场所,使用的较为广泛,同时它使用起来也较为方便省电。“人来灯亮,人走灯灭”的特性,使他们在部分场景…...
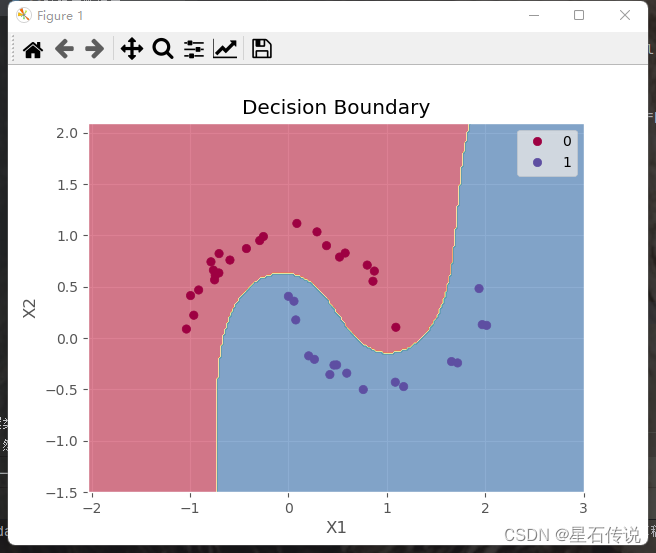
机器学习——支持向量机(SVM)
机器学习——支持向量机(SVM) 文章目录 前言一、SVM算法原理1.1. SVM介绍1.2. 核函数(Kernel)介绍1.3. 算法和核函数的选择1.4. 算法步骤1.5. 分类和回归的选择 二、代码实现(SVM)1. SVR(回归&a…...

HTTP协议初识·下篇
介绍 承接上篇:HTTP协议初识中篇_清风玉骨的博客-CSDN博客 本篇内容: 长链接 网络病毒 cookie使用&session介绍 基本工具介绍 postman 模拟客户端请求 fiddler 本地抓包的软件 https介绍 https协议原理 为什么加密 怎么加密 CA证书介绍 数字签名介绍…...

c++ 类的实例化顺序
其他类对象有作为本类成员,先构造类中的其他类对象, 释放先执行本对象的析构函数再执行包含的类对象的析构函数 #include <iostream> #include <string.h> using namespace std;class Phone { public:Phone(string name):m_PName(name){…...

Vue自动生成二维码并可下载二维码
遇到一个需求,需要前端自行生成用户的个人名片分享二维码,并提供二维码下载功能。在网上找到很多解决方案,最终吭哧吭哧做完了,把它整理记录一下,方便后续学习使用!嘿嘿O(∩_∩)O~ 这个小东西有以下功能特点…...
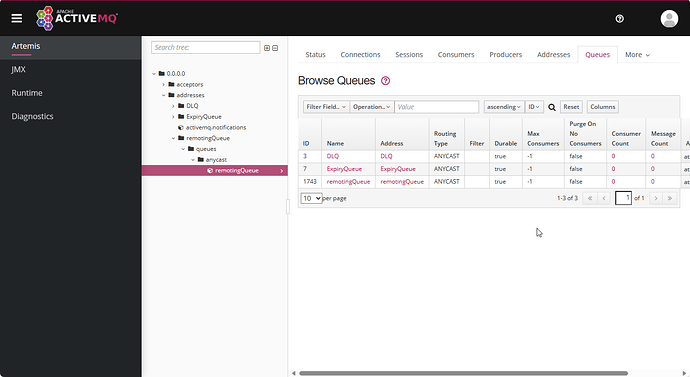
应该下那个 ActiveMQ
最近在搞 ActiveMQ 的时候,发现有 2 个 ActiveMQ 可以下载。 应该下那个呢? JMS 即Java Message Service,是JavaEE的消息服务接口。 JMS主要有两个版本:1.1和2.0。 2.0和1.1相比,主要是简化了收发消息的代码。 所谓…...

【C语言】指针详解(3)
大家好,我是苏貝,本篇博客带大家了解指针(2),如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 一.函数指针数组二.指向函数指针数组的指针(不重要)三.回调函数 一.函…...
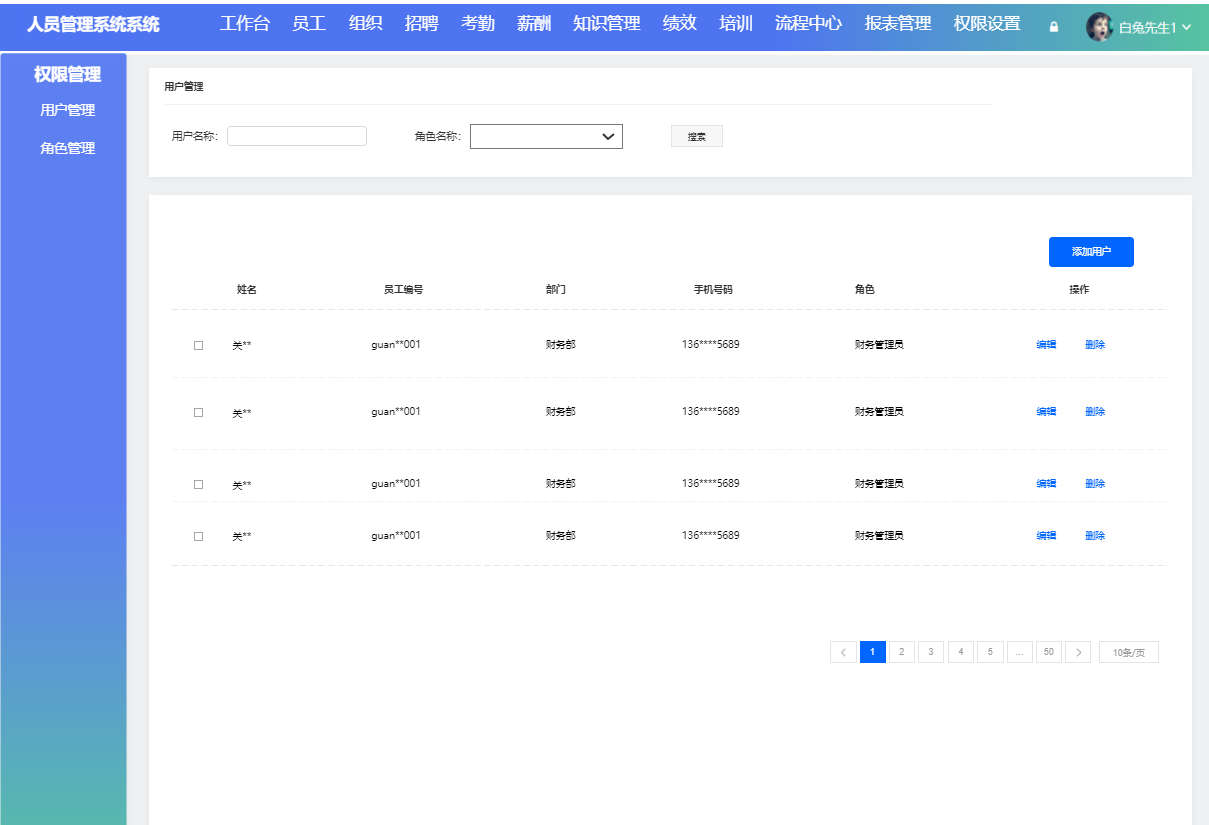
告别HR管理繁琐,免费低代码平台来帮忙
编者按:本文着重介绍了使用免费且高效的低代码平台实现的HR管理系统在一般日常人力资源管理工作中的关键作用。 关键词:低代码平台、HR管理系统 1.HR管理系统有什么作用? HR管理系统作为一款数字化工具,可为企业提供全方位的人力资…...

Java开发面试--Redis专区
1、 什么是Redis?它的主要特点是什么? 答: Redis是一个开源的、基于内存的高性能键值对存储系统。它主要用于缓存、数据存储和消息队列等场景。 高性能:Redis将数据存储在内存中,并采用单线程的方式处理请求…...
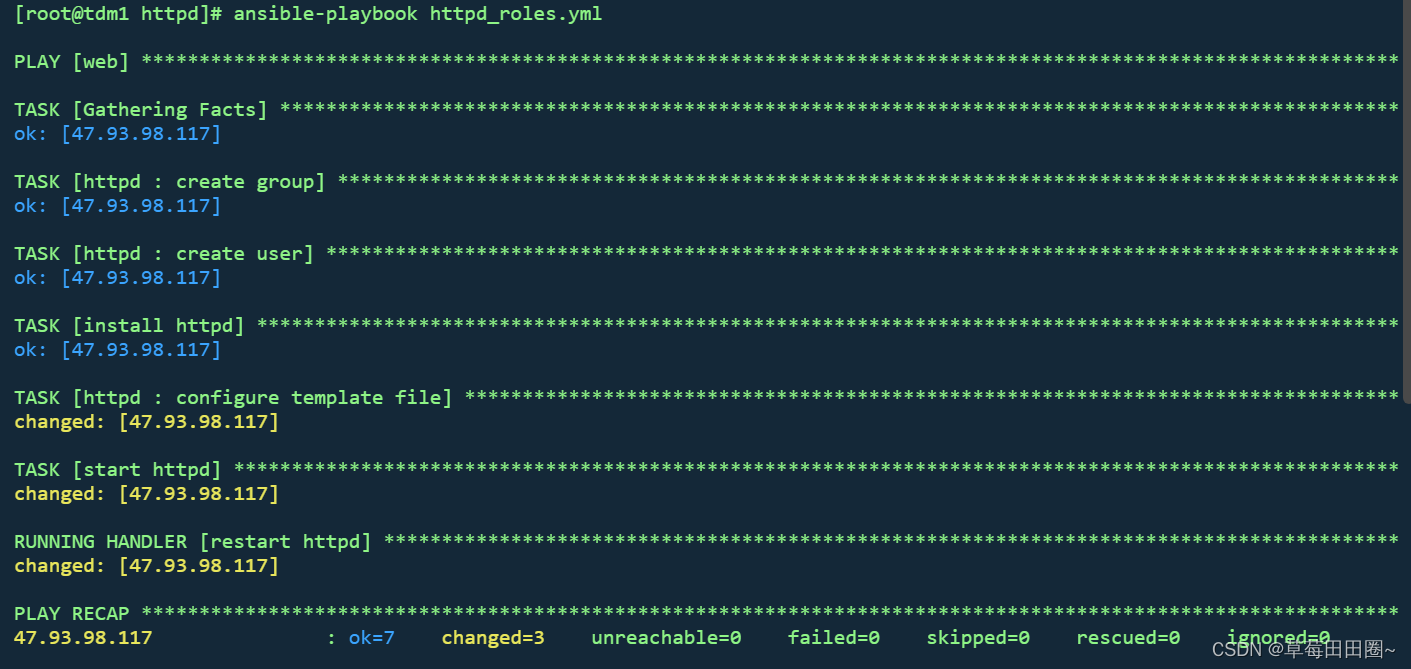
Ansible-roles学习
目录 一.roles角色介绍二.示例一.安装httpd服务 一.roles角色介绍 roles能够根据层次型结构自动装载变量文件,tasks以及handlers登。要使用roles只需在playbook中使用include指令即可。roles就是通过分别将变量,文件,任务,模块以…...
python3如何安装各类库的小总结
我的python3的安装路径是: C:\Users\Administrator\AppData\Local\Programs\Python\Python38 C:\Users\Administrator\AppData\Local\Programs\Python\Python38\python3.exeC:\Users\Administrator\AppData\Local\Programs\Python\Python38\Scripts C:\Users\Admin…...

ffmpeg 特效 转场 放大缩小
案例 ffmpeg \ -i input.mp4 \ -i image1.png \ -i image2.png \ -filter_complex \ [1:v]scale100:100[img1]; \ [2:v]scale1280:720[img2]; \ [0:v][img1]overlay(main_w-overlay_w)/2:(main_h-overlay_h)/2[bkg];\ [bkg][img2]overlay0:0 \ -y output.mp4 -i input.mp4//这…...

【GNN 03】PyG
工具包安装: 不要pip安装 https://github.com/pyg-team/pytorch_geometrichttps://github.com/pyg-team/pytorch_geometric import torch import networkx as nx import matplotlib.pyplot as pltdef visualize_graph(G, color):plt.figure(figsize(7, 7))plt.xtic…...

每日刷题-5
目录 一、选择题 二、算法题 1、不要二 2、把字符串转换成整数 一、选择题 1、 解析:printf(格式化串,参数1,参数2,.….),格式化串: printf第一个参数之后的参数要按照什么格式打印,比如%d--->按照整形方式打印&am…...
)
RNN简介(深入浅出)
目录 简介1. 基本理论 简介 要快速掌握RNN,可以考虑以下步骤: 学习基本理论:了解RNN的原理、结构和工作原理。掌握RNN的输入输出形式、时间步、隐藏状态、记忆单元等关键概念。学习常见的RNN变体:了解LSTM(Long Shor…...

Leetcode137. 某一个数字出现一次,其余数字出现3次
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法且使用常数级空…...
)
原子化CSS(Atomic CSS)
UnoCSS,它不是像TailWind CSS和Windi CSS属于框架,而是一个引擎,它没有提供预设的原子化CSS工具类。引用自掘金,文章中实现相同的功能,构建后的体积TailWind 远> Windi > UnoCSS,体积会小很多。 像这种原子性的…...

pandas 筛选数据的 8 个骚操作
日常用Python做数据分析最常用到的就是查询筛选了,按各种条件、各种维度以及组合挑出我们想要的数据,以方便我们分析挖掘。 东哥总结了日常查询和筛选常用的种骚操作,供各位学习参考。本文采用sklearn的boston数据举例介绍。 from sklearn …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
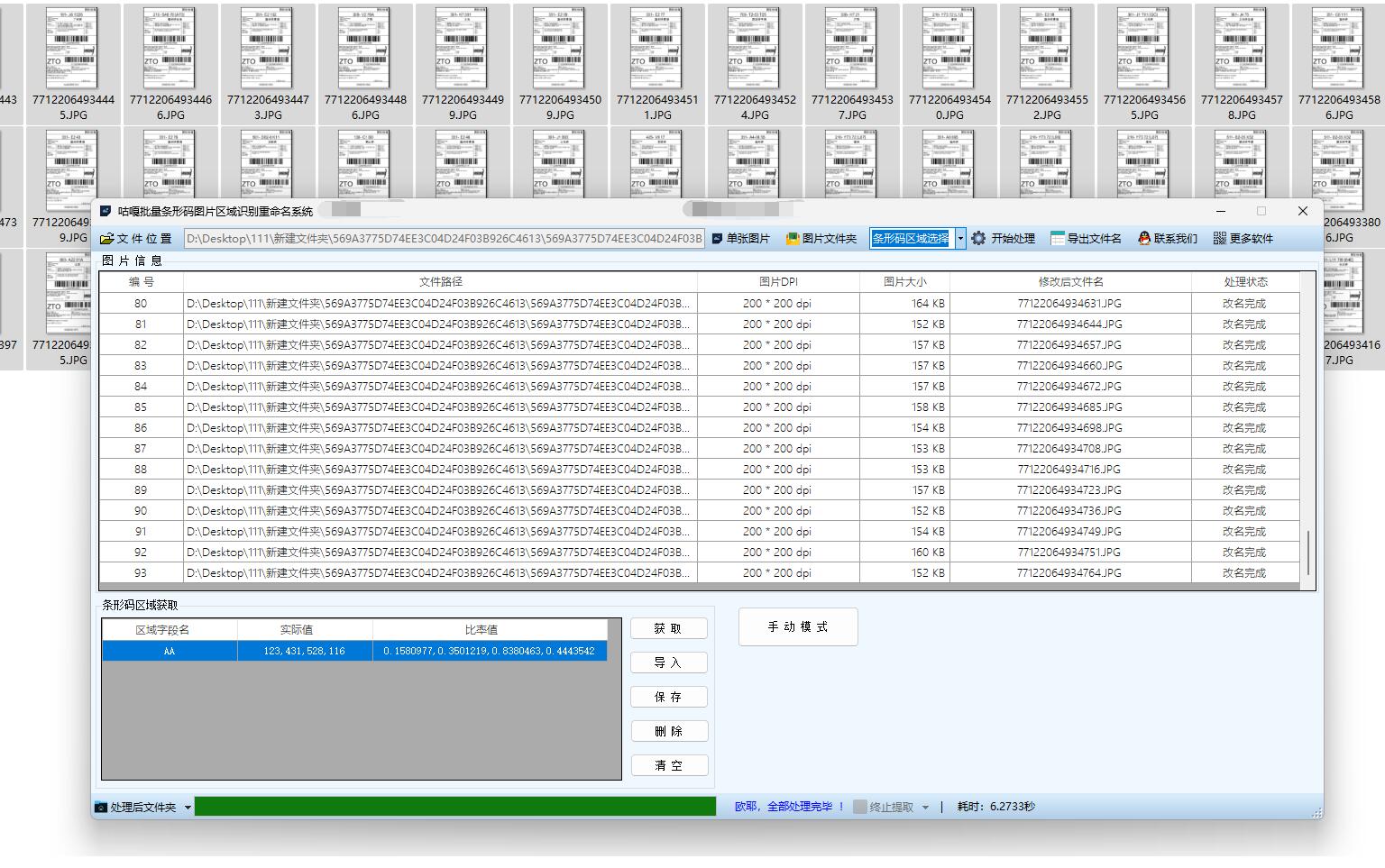
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...
)
iOS 项目怎么构建稳定性保障机制?一次系统性防错经验分享(含 KeyMob 工具应用)
崩溃、内存飙升、后台任务未释放、页面卡顿、日志丢失——稳定性问题,不一定会立刻崩,但一旦积累,就是“上线后救不回来的代价”。 稳定性保障不是某个工具的功能,而是一套贯穿开发、测试、上线全流程的“观测分析防范”机制。 …...

Angular中Webpack与ngx-build-plus 浅学
Webpack 在 Angular 中的概念 Webpack 是一个模块打包工具,用于将多个模块和资源打包成一个或多个文件。在 Angular 项目中,Webpack 负责将 TypeScript、HTML、CSS 等文件打包成浏览器可以理解的 JavaScript 文件。Angular CLI 默认使用 Webpack 进行项目…...
