算法刷题记录-树(LeetCode)
783. Minimum Distance Between BST Nodes
思路(DFS 中序遍历)
考虑中序遍历的性质即可
代码
class Solution {
public:int min_diff=numeric_limits<int>::max();int prev=numeric_limits<int>::min()+100000;int minDiffInBST(TreeNode* root) {inorderTraversal(root);return min_diff;}void inorderTraversal(TreeNode* root){if (root== nullptr){return ;}inorderTraversal(root->left);min_diff=min(min_diff,root->val-prev);prev=root->val;inorderTraversal(root->right);}
};
814. Binary Tree Pruning
思路(DFS)
对于一个节点是否删除,有如下几种情况:
863. All Nodes Distance K in Binary Tree
思路(DFS)
首先,需要通过dfs算法找到从原点到目标点的路径。 p a t h = [ 2 , 3 , 5 , 7 ] path=[2,3,5,7] path=[2,3,5,7], k = 2 k=2 k=2。其中7为目标点然后考虑对路径的每一节点,进行下列计算:
对于从原点到目标节点的路径。由目标点至上逐级考虑:
- 对于目标点7,需要考虑所有距离目标节点距离为k的子节点(DFS)
- 对于目标上一个节点5,从7至5的距离为1,因此考虑与5距离为1的子节点,同时将7设为已访问,防止重复遍历。
- 。。。以此类推
代码
class Solution {
public:vector<int> ans;vector<TreeNode*> _path;vector<TreeNode*> path;unordered_set<int> visited;vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {_path.push_back(root);findPath(root,target->val);findNodes(path.back(),k);path.pop_back();k--;visited.insert(target->val);int size=path.size()-1;for (int i = size; i >=0 ; i--) {findNodes(path[i],k);visited.insert(path[i]->val);k--;}return ans;}void findPath(TreeNode* root,int target){if (root->val==target){for (auto curr:_path) {path.push_back(curr);}return;}if (root->left){_path.push_back(root->left);findPath(root->left,target);_path.pop_back();}if (root->right){_path.push_back(root->right);findPath(root->right,target);_path.pop_back();}}void findNodes(TreeNode* root,int distance){if (distance==0&&!visited.count(root->val)){ans.push_back(root->val);visited.insert(root->val);}else {if (root->left&&!visited.count(root->left->val)){findNodes(root->left,distance-1);}if (root->right&&!visited.count(root->right->val)){findNodes(root->right,distance-1);}}}
};
865. Smallest Subtree with all the Deepest Nodes
思路 DFS
在遍历时带有层数信息以及路径信息即可,通过DFS遍历获取最深层的节点以及其路径,然后通过从头到尾遍历确认那一层是最后的公共节点。
代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {ArrayList<TreeNode> path = new ArrayList<>();int max_depth = 0;ArrayList<ArrayList<TreeNode>> res = new ArrayList<>();public TreeNode subtreeWithAllDeepest(TreeNode root) {path.add(root);dfs(root, 1);if (res.size() == 1) {int len = res.get(0).size();return res.get(0).get(len - 1);}TreeNode prev = null;for (int i = 0; i < res.get(0).size(); i++) {int first = res.get(0).get(i).val;for (int j = 1; j < res.size(); j++) {if (res.get(j).get(i).val != first) {return prev;}}prev = res.get(0).get(i);}return prev;}public void dfs(TreeNode node, int depth) {if (node.left == null && node.right == null) {if (depth < max_depth) {return;}if (depth > max_depth) {res.clear();max_depth = depth;}res.add(new ArrayList<>(path));return;}if (node.left != null) {path.add(node.left);dfs(node.left, depth + 1);path.remove(path.size() - 1);}if (node.right != null) {path.add(node.right);dfs(node.right, depth + 1);path.remove(path.size() - 1);}}
}
Complete Binary Tree Inserter
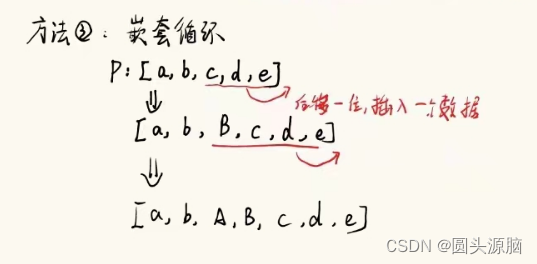
思路 双队列
定义upper为上层还有子树空间的树节点队列,next为当前层树节点队列。例如在下图中,upper存储[2,3],next存储[4]。

upper存储[3],next存储[4]。

当树为完全二叉树时next队列为空,例如下面的情况中,upper存储[4,5,6,7],next为空:

在我们插入时,我们只需查看upper队列中是否还有元素,若有元素在upper中,则去除队列头节点,向其中插入新的树节点,并在next中加入子节点。如果该节点左右子节点插满,则upper移除该节点。
如果upper为空,则next成为新的upper、next为空。
代码
public class CBTInserter {Queue<TreeNode> upper;Queue<TreeNode> next;TreeNode root;public CBTInserter(TreeNode root) {upper = new LinkedList<>();next = new LinkedList<>();this.root = root;upper.offer(root);if (root.left != null) {next.offer(root.left);}if (root.right != null) {next.offer(root.right);}if (next.size()==2&&root.left.left==null){upper.clear();upper.addAll(next);next.clear();}while (!next.isEmpty() && next.peek().left != null) {int size = next.size();Queue<TreeNode> emptyQueue = new LinkedList<>();upper = emptyQueue;while (size > 0) {TreeNode node = next.poll();if (node.left != null) {next.offer(node.left);}if (node.right != null) {next.offer(node.right);}if (node.left == null || node.right == null) {upper.offer(node);}size--;}}}public int insert(int val) {if (upper.isEmpty()) {refreshQueue();}TreeNode first = upper.peek();int parent_val = first.val;if (first.left == null) {first.left = new TreeNode(val);next.offer(first.left);} else {first.right = new TreeNode(val);next.offer(first.right);upper.poll();}return parent_val;}public TreeNode get_root() {return root;}public void refreshQueue() {upper = next;}
}
**968. Binary Tree Cameras
思路 贪心+DFS+状态转移
这道题目其实不是那么好理解的,题目举的示例不是很典型,会误以为摄像头必须要放在中间,其实放哪里都可以只要覆盖了就行。
这道题目难在两点:
- 需要确定遍历方式
- 需要状态转移的方程
我们之前做动态规划的时候,只要最难的地方在于确定状态转移方程,至于遍历方式无非就是在数组或者二维数组上。
需要确定遍历方式
首先先确定遍历方式,才能确定转移方程,那么该如何遍历呢?
在安排选择摄像头的位置的时候,我们要从底向上进行推导,因为尽量让叶子节点的父节点安装摄像头,这样摄像头的数量才是最少的 ,这也是本道贪心的原理所在!
如何从低向上推导呢?
就是后序遍历也就是左右中的顺序,这样就可以从下到上进行推导了。
后序遍历代码如下:
int traversal(TreeNode* cur) {// 空节点,该节点有覆盖if (终止条件) return ;int left = traversal(cur->left); // 左int right = traversal(cur->right); // 右逻辑处理 // 中return ;}
注意在以上代码中我们取了左孩子的返回值,右孩子的返回值,即 left 和 right, 以后推导中间节点的状态
需要状态转移的方程
确定了遍历顺序,再看看这个状态应该如何转移,先来看看每个节点可能有几种状态:
可以说有如下三种:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
那么问题来了,空节点究竟是哪一种状态呢? 空节点表示无覆盖? 表示有摄像头?还是有覆盖呢?
回归本质,为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
那么空节点不能是无覆盖的状态,这样叶子节点就可以放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了
接下来就是递推关系。
那么递归的终止条件应该是遇到了空节点,此时应该返回 2(有覆盖),原因上面已经解释过了。
// 空节点,该节点有覆盖if (cur == NULL) return 2;
递归的函数,以及终止条件已经确定了,再来看单层逻辑处理。
主要有如下四类情况:
情况1:左右节点都有覆盖
左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。
如图:

代码如下:
// 左右节点都有覆盖if (left == 2 && right == 2) return 0;
情况2:左右节点至少有一个无覆盖的情况
如果是以下情况,则中间节点(父节点)应该放摄像头:
left == 0 && right == 0 - 左右节点无覆盖
left == 1 && right == 0- 左节点有摄像头,右节点无覆盖
left == 0 && right == 1- 左节点有无覆盖,右节点摄像头
left == 0 && right == 2 - 左节点无覆盖,右节点覆盖
left == 2 && right == 0 - 左节点覆盖,右节点无覆盖
这个不难理解,毕竟有一个孩子没有覆盖,父节点就应该放摄像头。
此时摄像头的数量要加一,并且 return 1,代表中间节点放摄像头。
代码如下:
if (left == 0 || right == 0) {result++;return 1;}
情况3:左右节点至少有一个有摄像头
如果是以下情况,其实就是 左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
left == 1 && right == 2 左节点有摄像头,右节点有覆盖
left == 2 && right == 1 左节点有覆盖,右节点有摄像头
left == 1 && right == 1 左右节点都有摄像头
代码如下:
if (left == 1 || right == 1) return 2;
从这个代码中,可以看出,如果 left == 1, right == 0 怎么办?其实这种条件在情况 2 中已经判断过了,如图:

这种情况也是大多数同学容易迷惑的情况。
情况4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图:
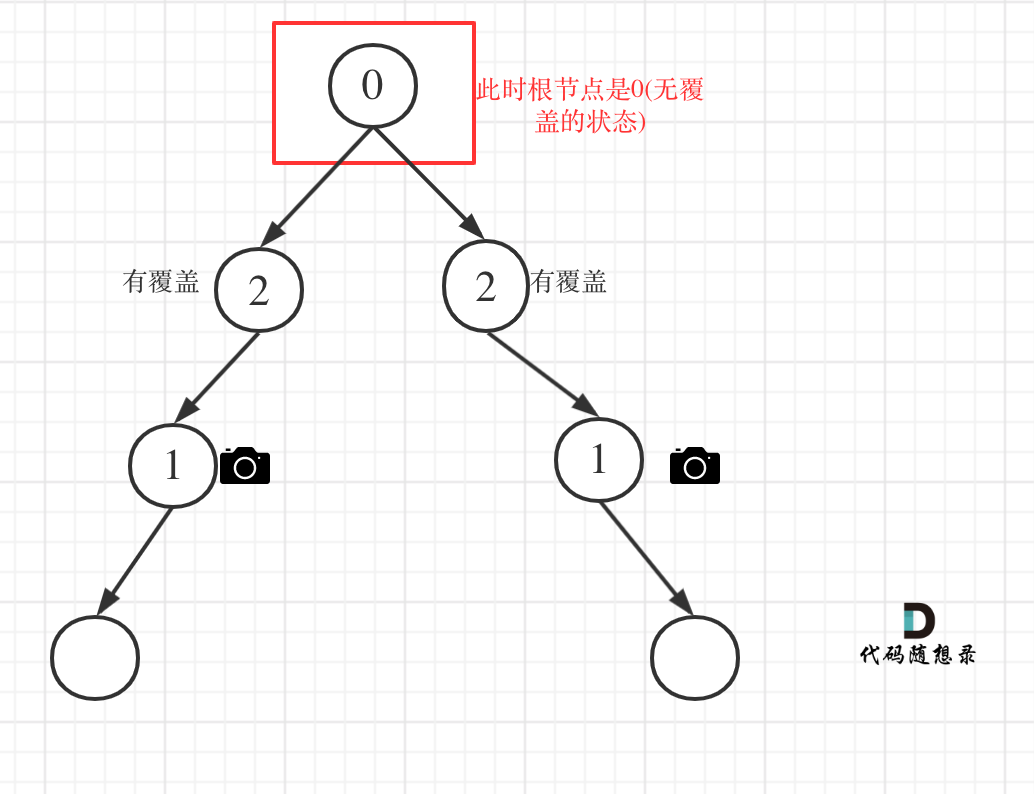
所以递归结束之后,还要判断根节点,如果没有覆盖,result++,代码如下:
int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
代码
class Solution {
private:int result;int traversal(TreeNode* cur) {// 空节点,该节点有覆盖if (cur == NULL) return 2;int left = traversal(cur->left); // 左int right = traversal(cur->right); // 右// 情况1// 左右节点都有覆盖if (left == 2 && right == 2) return 0;// 情况2// left == 0 && right == 0 左右节点无覆盖// left == 1 && right == 0 左节点有摄像头,右节点无覆盖// left == 0 && right == 1 左节点有无覆盖,右节点摄像头// left == 0 && right == 2 左节点无覆盖,右节点覆盖// left == 2 && right == 0 左节点覆盖,右节点无覆盖if (left == 0 || right == 0) {result++;return 1;}// 情况3// left == 1 && right == 2 左节点有摄像头,右节点有覆盖// left == 2 && right == 1 左节点有覆盖,右节点有摄像头// left == 1 && right == 1 左右节点都有摄像头// 其他情况前段代码均已覆盖if (left == 1 || right == 1) return 2;// 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解// 这个 return -1 逻辑不会走到这里。return -1;}public:int minCameraCover(TreeNode* root) {result = 0;// 情况4if (traversal(root) == 0) { // root 无覆盖result++;}return result;}
};
1123. Lowest Common Ancestor of Deepest Leaves(与865重复)
思路 DFS
同865
代码
同865
1448. Count Good Nodes in Binary Tree
思路 BFS
每次遍历时,带着先前节点的最大值。若当前节点值大于等于先前的最大值,则结果+1,并更新最大值。递归遍历其左右子节点。
代码
class Solution {int ans=0;public int goodNodes(TreeNode root) {goodNodesImpl(root,Integer.MIN_VALUE);return ans;}public void goodNodesImpl(TreeNode root,int prevMax){if (root==null){return;}if (prevMax<=root.val){ans++;prevMax=root.val;}goodNodesImpl(root.left,prevMax);goodNodesImpl(root.right,prevMax);}
}
相关文章:

算法刷题记录-树(LeetCode)
783. Minimum Distance Between BST Nodes 思路(DFS 中序遍历) 考虑中序遍历的性质即可 代码 class Solution { public:int min_diffnumeric_limits<int>::max();int prevnumeric_limits<int>::min()100000;int minDiffInBST(TreeNode* root) {inorderTraversa…...
Linux中安装MySQL_图解_2023新
1.卸载 为了避免不必要的错误发生,先将原有的文件包进行查询并卸载 // 查询 rpm -qa | grep mysql rpm -qa | grep mari// 卸载 rpm -e 文件名 --nodeps2.将安装包上传到指定文件夹中 这里采用的是Xftp 3.将安装包进行解压 tar -zxvf 文件名 -C 解压路径4.获取解压的全路…...

生产设备上的静电该如何处理?
在工厂生产车间里有很多机械设备,在生产运作过程中,难免会产生大量静电,静电会产生许多危害。 例如,1、会使电子设备故障、误操作而引起的电磁干扰。 2、电子元件或集成电路的静电击穿; 3、高压静电放电引起触电; 4、静电放电引起…...
山洪灾害预警方案(山洪预警解决方案的组成)
随着气候变化的不断加剧,山洪灾害在许多地区成为了极具威胁性的自然灾害之一。为了帮助地方政府和居民更好地预防和应对山洪灾害,我们设计了一套基于星创易联的SR600工业路由器和DTU200的山洪灾害预警方案,并成功在某地区进行了部署。 案…...

数据库 MVCC 详解
目录 1. 什么是 MVCC? 2. MVCC 的好处? 3. 快照读?当前读分别是什么?怎么理解? 3.1 快照读 3.2 当前读 4. 数据库的四种隔离级别 5. MVCC 实现原理 5.1 隐藏字段 5.2 undo log(版本链) 5.3 readView 6. re…...

process.nextTick和vue的nextTick区别
事情的起因是代码里用了nextTick,然后提交代码的时候才发现,引入的是process的,然后改成了使用vue的nextTick发现效果不生效了,然后百度查了查两者的区别: process.nextTick是nodejs自带的,而在浏览器中执…...
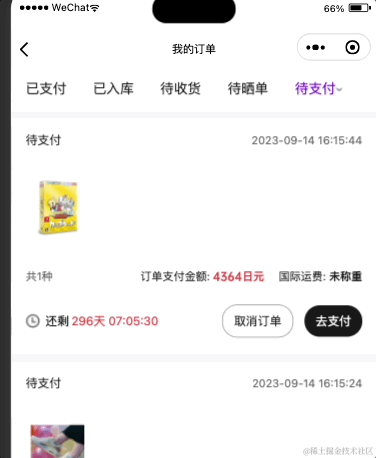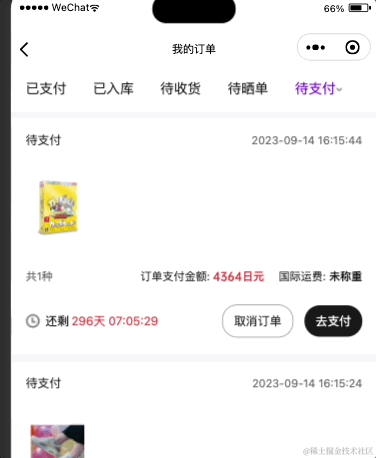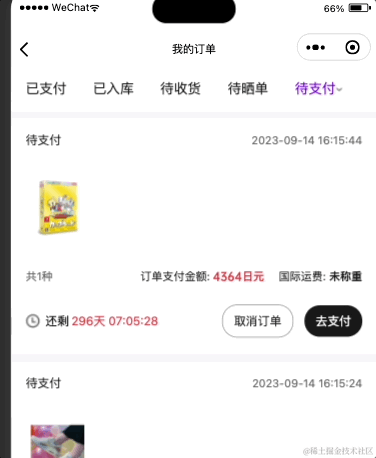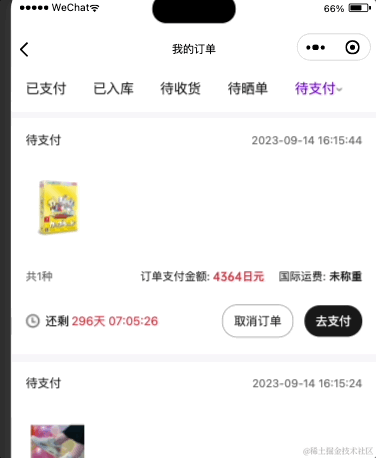
小程序实现一个 倒计时组件
小程序实现一个 倒计时组件 需求背景 要做一个倒计时,可能是天级别,也可能是日级别,时级别,而且每个有效订单都要用,就做成组件了 效果图 需求分析 需要一个未来的时间戳,或者在服务度直接下发一个未来…...

【四万字】网络编程接口 Socket API 解读大全
Socket 是网络协议栈暴露给编程人员的 API,相比复杂的计算机网络协议,API 对关键操作和配置数据进行了抽象,简化了程序编程。 本文讲述的 socket 内容源自 Linux man。本文主要对各 API 进行详细介绍,从而更好的理解 socket 编程。…...

无涯教程-JavaScript - ISREF函数
描述 如果指定的值是参考,则ISREF函数返回逻辑值TRUE。否则返回FALSE。 语法 ISREF (value) 争论 Argument描述Required/OptionalvalueA reference to a cell.Required Notes 您可以在执行任何操作之前使用此功能测试单元格的内容。 适用性 Excel 2007,Excel 2010,Exce…...

Android:获取MAC < 安卓系统11 <= 获取UUID
1.核心代码 主要的UseMac.java import android.annotation.SuppressLint; import android.content.Context; import android.net.ConnectivityManager; import android.net.NetworkInfo; import android.net.wifi.WifiInfo; import android.net.wifi.WifiManager; import an…...

线程的几种状态
目标: 1. 线程的几种状态的含义 2. 状态之间的切换条件 目录 新建(new)线程 可运行(Runnable)状态 运行(Running)状态 阻塞(Blocked)状态 等待(Waiting…...
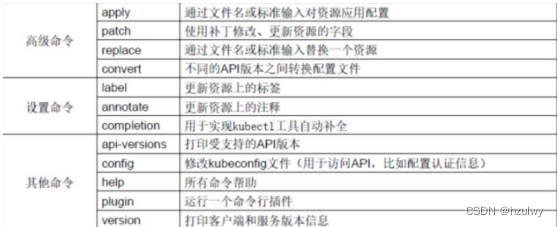
kubernetes集群yaml文件与kubectl工具
k8s集群中对资源管理和资源对象编排部署都可以通过声明样式(yaml)文件来解决,也就是可以把需要对资源对象操作编辑到yaml格式文件中,我们把文件叫做资源清单文件,通过kubectl命令直接使用资源清单文件就可以实现对大量的资源对象进行编排部署…...
)
python基础语法(三)
感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接 🐒🐒🐒个人主页 🥸🥸🥸C语言 🐿️🐿️🐿️C语言例题 🐣🐓🏀python 运…...
Haproxy集群与常见的Web集群调度器
文章目录 1. Web集群调度器概述1.1 Web集群调度器简介1.2 调度器类别1.2.1 常用软件类1.2.2 常用硬件类 2. Haproxy软件介绍2.1 Haproxy简介2.2 支持功能2.3 主要特性2.4 常用调度算法2.4.1 轮询:RR(Round Robin)2.4.2 最小连接数:…...

centos免密登录
centos免密登录 小白教程,一看就会,一做就成。 1.知道服务器密码的情况 ssh-keygen -t rsa #上面的命令后三次回车#然后把想要免密登录的服务器加进来 ssh-copy-id -i /root/.ssh/id_rsa.pub root192.168.10.115 #免密码登录被控的主机(ip是…...

学Python的漫画漫步进阶 -- 第十四步
学Python的漫画漫步进阶 -- 第十四步 十四、网络通信14.1 基本的网络知识14.1.1 TCP/IP14.1.2 IP地址14.1.3 端口14.1.4 HTTP/HTTPS 14.2 搭建自己的Web服务器14.3 urllib.request模块14.3.1 发送GET请求14.3.2 发送POST请求 14.4 JSON数据14.4.1 JSON文档的结构14.4.2 JSON数据…...

OpenCV(四十二):Harris角点检测
1.Harris角点介绍 什么是角点? 角点指的是两条边的交点,图中红色圈起来的点就是角点。 Harris角点检测原理:首先定义一个矩形区域,然后将这个矩形区域放置在我的图像中,求取这个区域内所有的像素值之和,之…...
C++数据结构题:DS 顺序表--连续操作
建立顺序表的类,属性包括:数组、实际长度、最大长度(设定为 1000 ) 该类具有以下成员函数: 构造函数:实现顺序表的初始化。 插入多个数据的 multiinsert(int i, int n, int item[]) 函数,实…...

DM@命题公式@主范式的性质和应用@数理逻辑解决数字电路全加器问题
文章目录 abstract主合取范式与主析取范式间的关系👺主范式存在及唯一性定理例 主范式的性质👺求公式的成真与成假赋值主析取范式直接得到主合取范式 判断公式的类型 n n n元命题公式的主析取范式(主合取范式)的个数判断两个命题公式是否等值 给出一个满…...
基于微信小程序+Springboot线上租房平台设计和实现【三端实现小程序+WEB响应式用户前端+后端管理】
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
