c++分层最短路(洛谷飞行路线)acwing版
分层最短路算法是在SPFA算法的基础上,将每个点分成若干层,从而使得每个点之间的转移只在同一层次或上下两个相邻层次之间进行,减少了每轮的迭代次数,优化了算法的效率。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>using namespace std;const int MAXN = 10005;
const int MAXM = 100005;
const int INF = 0x3f3f3f3f;struct Edge {int to, nxt, w;
} e[MAXM];int head[MAXN], tot;
int dis[MAXN], vis[MAXN];inline void add(int u, int v, int w) {e[++tot].nxt = head[u];e[tot].to = v;e[tot].w = w;head[u] = tot;
}void spfa(int s) {memset(dis, 0x3f, sizeof(dis));dis[s] = 0;queue<int> q;q.push(s);while (!q.empty()) {int u = q.front();q.pop();vis[u] = false;for (int i = head[u]; i; i = e[i].nxt) {int v = e[i].to;if (dis[v] > dis[u] + e[i].w) {dis[v] = dis[u] + e[i].w;if (!vis[v]) {q.push(v);vis[v] = true;}}}}
}int main() {int n, m;scanf("%d%d", &n, &m);tot = 0;memset(head, 0, sizeof(head));for (int i = 1; i <= m; ++i) {int u, v, w;scanf("%d%d%d", &u, &v, &w);add(u, v, w);}int s, t;scanf("%d%d", &s, &t);spfa(s);printf("%d\n", dis[t]);return 0;
}
int layer[MAXN]; //记录每个点所在的层次
int check_layer[MAXN]; //记录每个点是否在队列中void layer_spfa(int s) {memset(dis, 0x3f, sizeof(dis));dis[s] = 0;layer[s] = 0;queue<int> q;q.push(s);check_layer[s] = true;while (!q.empty()) {int u = q.front();q.pop();check_layer[u] = false;for (int i = head[u]; i; i = e[i].nxt) {int v = e[i].to;if (layer[u] == layer[v]) {if (dis[v] > dis[u] + e[i].w) {dis[v] = dis[u] + e[i].w;if (!check_layer[v]) {q.push(v);check_layer[v] = true;}}} else if (layer[v] > layer[u]) { //分层if (dis[v] > dis[u] + e[i].w) {dis[v] = dis[u] + e[i].w;layer[v] = layer[u] + 1;if (!check_layer[v]) {q.push(v);check_layer[v] = true;}}}}}
}
先看题目:
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 nn 个城市设有业务,设这些城市分别标记为 00 到 n-1n−1,一共有 mm 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 kk 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
输入格式
第一行三个整数 n,m,kn,m,k,分别表示城市数,航线数和免费乘坐次数。
接下来一行两个整数 s,ts,t,分别表示他们出行的起点城市编号和终点城市编号。
接下来 mm 行,每行三个整数 a,b,ca,b,c,表示存在一种航线,能从城市 aa 到达城市 bb,或从城市 bb 到达城市 aa,价格为 cc。
输出格式
输出一行一个整数,为最少花费。
输入样例:
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100输出样例:
8先给出具体代码:
#include<cstring>
#include<iostream>
#include<queue>using namespace std;typedef pair<int, int> PII;const int N = 2100010, INF = 0x3f3f3f3f;int n, m, k, s, t;
int dist[N];
int h[N], w[N], e[N], ne[N], idx;
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void dijkstra(int u)
{memset(dist, INF, sizeof dist);dist[u] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, u});while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second ,distance = t.first;if(st[ver]) continue;st[ver] = true;for(int i = h[ver]; ~i; i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}
}int main()
{cin >> n >> m >> k >> s >> t;memset(h, -1, sizeof h);while(m --){int a, b, c;scanf("%d%d%d", &a, &b ,&c);add(a, b, c), add(b, a, c);for(int j = 1; j <= k; j ++){add(j * n + a, j * n + b, c);add(j * n + b, j * n + a, c);add((j - 1) * n + a, j * n + b, 0);add((j - 1) * n + b, j * n + a, 0);}}for(int i = 0; i < k; i ++) add(i * n + t, (i + 1) * n + t, 0);dijkstra(s);printf("%d\n", dist[n * k + t]);return 0;
}1:解释数据:2≤n≤10^4,1≤m≤10^5,0≤k≤10,0≤s, t, a, b<n, a != b, 0≤c≤10^3
本来数据最大值是m,双向边开两倍就可以,但是这里是分层建图,最多有十层,所以要再乘以十
2:初始化h数组
3、加边,下面的是分层建图
建图:从0到k层建k+1张图
各层之间从上到下建边花费为0
为防止使用小于k次权力就到达终点,在每层的终点间建花费为0的边连起来
4、dijkstra堆优化版的模板
5、答案输出:到k层的终点为答案
相关文章:
acwing版)
c++分层最短路(洛谷飞行路线)acwing版
分层最短路算法是在SPFA算法的基础上,将每个点分成若干层,从而使得每个点之间的转移只在同一层次或上下两个相邻层次之间进行,减少了每轮的迭代次数,优化了算法的效率。 #include <iostream> #include <cstdio> #inc…...

Python bs4 BeautifulSoup库使用记录
目录 介绍 安装 初始化 解析器 使用方法 优势 Python标准库 lxml HTML lxml XML html5lib 格式化输出 对象 tag Name 多值属性 其他方法 NavigableString BeautifulSoup Comment 遍历 子节点 父节点 兄弟节点 回退和前进 搜索 过滤器 字符串 正则表达…...
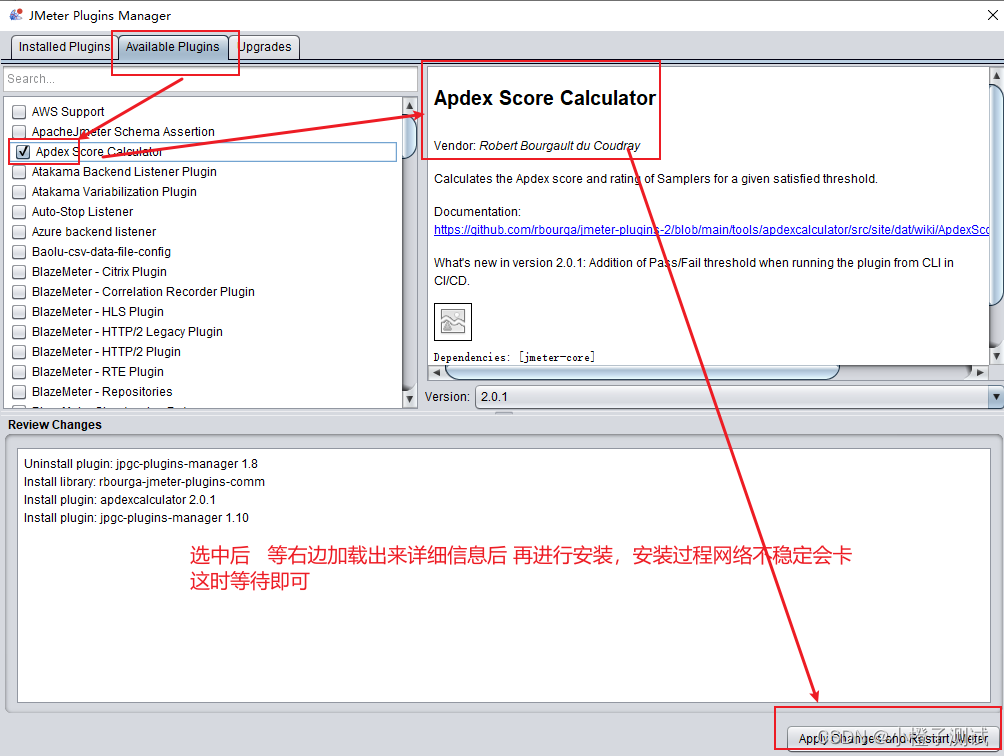
Jmeter系列-插件安装(5)
前言 jmeter4.0以上,如现在最新的5.2.1版本是有集成插件的只需要在官网下载 plugins-manager.jar 包,放在jmeter安装路径的lib/ext目录下即可使用:https://jmeter-plugins.org/install/Install/但并不能满足所有需求,仍然需要安装…...

spring aop源码解析
spring知识回顾 spring的两个重要功能:IOC、AOP,在ioc容器的初始化过程中,会触发2种处理器的调用, 前置处理器(BeanFactoryPostProcessor)后置处理器(BeanPostProcessor)。 前置处理器的调用时机是在容器基本创建完成时ÿ…...
控制物体移动、旋转)
使用Unity的Input.GetAxis(““)控制物体移动、旋转
使用Unity的Input.GetAxis("")控制物体移动、旋转 Input.GetAxis("") 是 Unity 引擎中的一个方法,用于获取游戏玩家在键盘或游戏手柄上输入的某个轴(Axis)的值。这里的 "" 是一个字符串参数,表示要…...

【CSS】画个三角形或圆形或环
首先通过调整边框,我们可以发现一些端倪 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><style>.box{width: 150px;height:150px;border: 50px solid black;}</style&g…...

AI项目六:基于YOLOV5的CPU版本部署openvino
若该文为原创文章,转载请注明原文出处。 一、CPU版本DEMO测试 1、创建一个新的虚拟环境 conda create -n course_torch_openvino python3.8 2、激活环境 conda activate course_torch_openvino 3、安装pytorch cpu版本 pip install torch torchvision torchau…...

记录YDLidar驱动包交叉编译时出现的一点问题
由于一不小心把交叉编译的系统根目录破坏了,所以一股脑将交叉编译系统根目录全删了重新安装,安装后,交叉编译发现ydlidar的ros包驱动出现了库无法链接的错误(刚刚还是好好的),但是又想不起来之前是怎么解决的了,所以还…...

嵌入式学习笔记(32)S5PV210的向量中断控制器
6.6.1异常处理的2个阶段 可以将异常处理分为2个阶段来理解。第一个阶段是异常向量表跳转;第二个阶段是进入了真正的异常处理程序irq_handler之后的部分。 6.6.2回顾:中断处理的第一个阶段(异常向量表跳转阶段)处理 (…...

linux下安装qt、qt触摸屏校准tslib
linux下安装qt 在 Linux 系统下安装 Qt,可以通过以下步骤进行操作:1. 下载 Qt 安装包:首先,你需要从 Qt 官方网站(https://www.qt.io/)下载适用于 Linux 的 Qt 安装包。选择与你的系统和需求相匹配的版本&…...

C++之unordered_map,unordered_set模拟实现
unordered_map,unordered_set模拟实现 哈希表源代码哈希表模板参数的控制仿函数增加正向迭代器实现*运算符重载->运算符重载运算符重载! 和 运算符重载begin()与end()实现 unordered_set实现unordered_map实现map/set 与 unordered_map/unordered_set对比哈希表…...

React Router,常用API有哪些?
react-router React Router是一个用于构建单页面应用程序(SPA)的库,它是用于管理React应用中页面导航和路由的工具。SPA是一种Web应用程序类型,它在加载初始页面后,通过JavaScript来动态加载并更新页面内容࿰…...

JVM类加载和双亲委派机制
当我们用java命令运行某个类的main函数启动程序时,首先需要通过类加载器把类加载到JVM,本文主要说明类加载机制和其具体实现双亲委派模式。 一、类加载机制 类加载过程: 类加载的过程是将类的字节码加载到内存中的过程,主要包括…...

P-MVSNet ICCV-2019 学习笔记总结 译文 深度学习三维重建
文章目录 5 P-MVSNet ICCV-20195.0 主要特点5.1 文章概述5.2 研究方法5.2.1 特征提取5.2.2 学习局域匹配置信5.2.3 深度图预测5.2.4 Loss方程MVSNet系列最新顶刊 对比总结5 P-MVSNet ICCV-2019 深度学习三维重建 P-MVSNet-ICCV-2019(原文、译文、批注) 下载 5.0 主要特点 …...
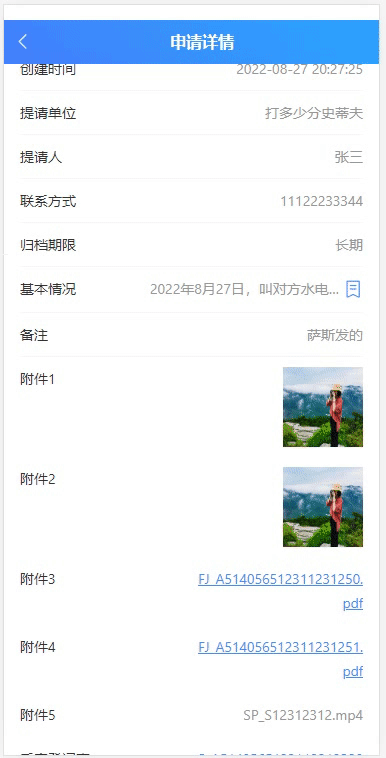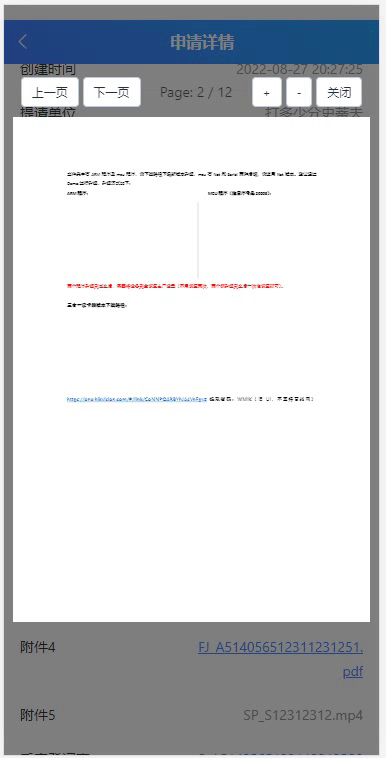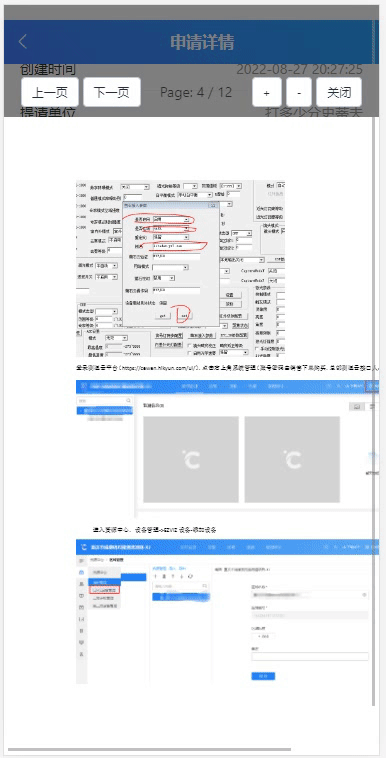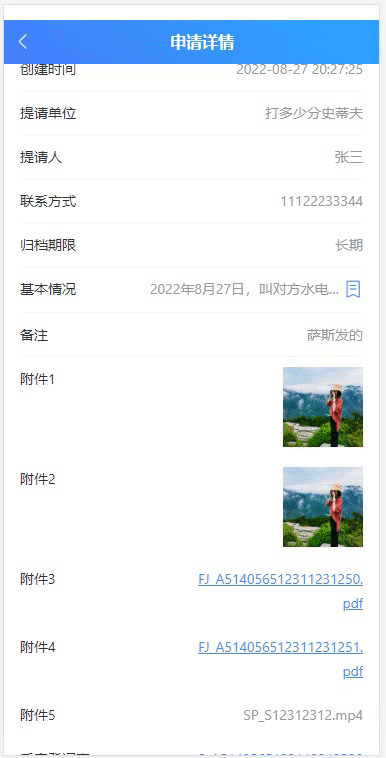
vueshowpdf 移动端pdf文件预览
1、安装 npm install vueshowpdf -S2、参数 属性说明类型默认值v-model是否显示pdf--pdfurlpdf的文件地址String- scale 默认放大倍数 Number1.2 minscale 最小放大倍数 Number0.8 maxscale 最大放大倍数 Number2 3、事件 名称说明回调参数closepdf pdf关闭事件-pdferr文…...

C#根据excel文件中的表头创建数据库表
C#根据excel文件中的表头创建数据库表 private void button1_Click(object sender, EventArgs e){string tableName tableNameTextBox.Text;string connectionString "";using (OpenFileDialog openFileDialog new OpenFileDialog()){openFileDialog.Filter &quo…...
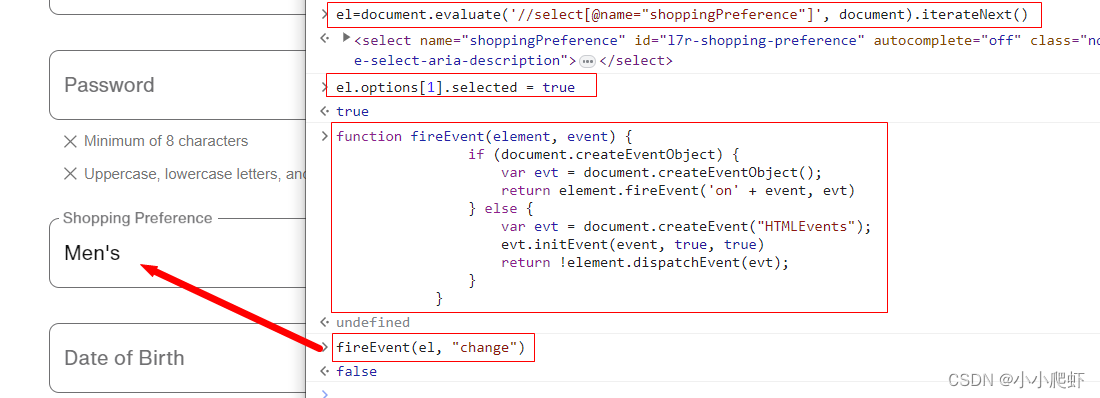
js通过xpath定位元素并且操作元素以下拉框select为例
js也可以使用xpath定位元素,现在实例讲解。 页面上有一个下拉框,里面内容有三个,用F12看一下 一、使用xpath定位这个下拉框select eldocument.evaluate(//select[name"shoppingPreference"], document).iterateNext()二、为下拉框…...
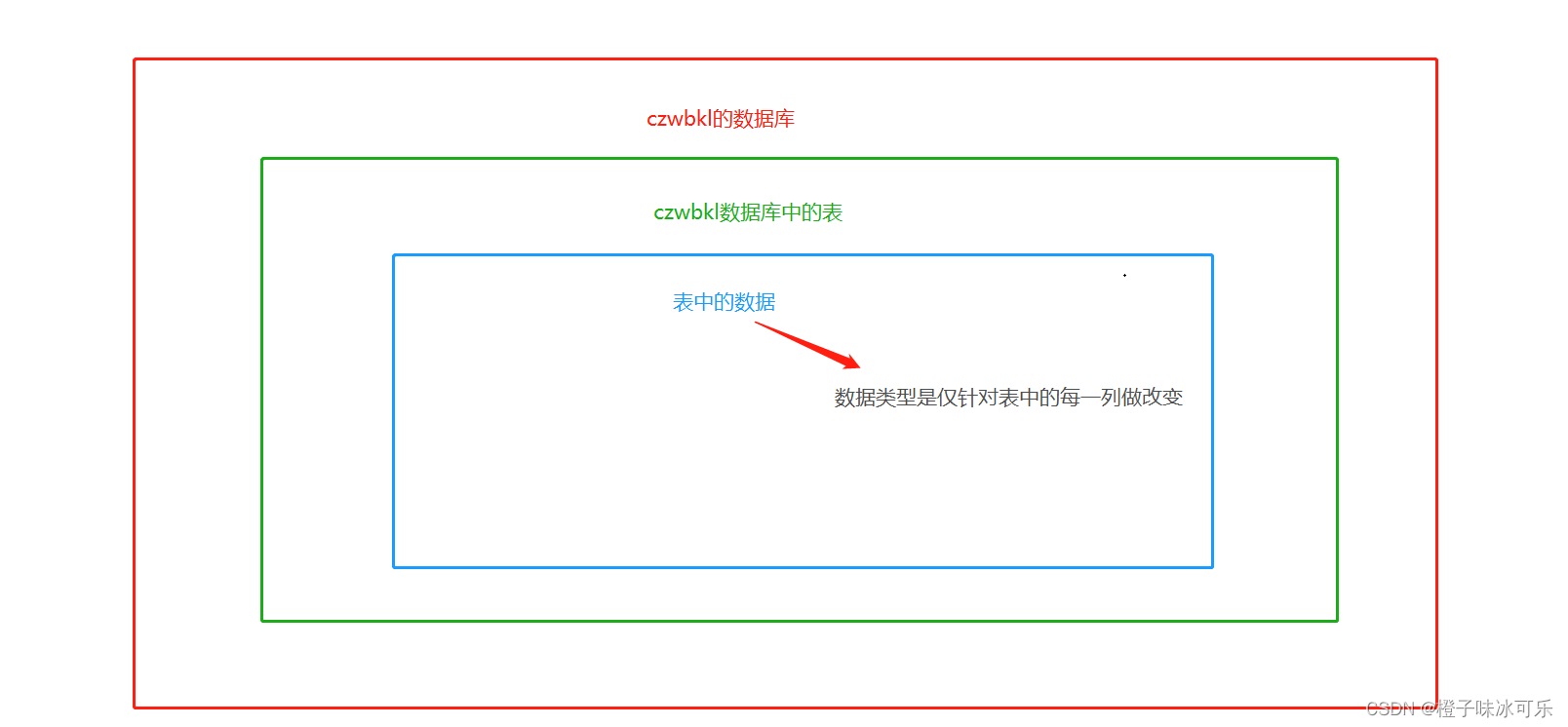
数据类型
目录 1.数值类型 整数类型 int 小数类型 double 2.字符类型 固定长度字符串 char 可变长度字符串 varchar 3.日期时间类型 日期类型:date 日期时间类型:datetime MySQL从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article…...

vue 模板应用
一,模板应用也就是对DOM的操作 二,如何使用 通过标签里面添加ref 和vue中使用 this.$refs.ref的名字.操作 进行使用 <template><h3>模板引用</h3><div ref"cont" class"cont">{{ content }}</div>&…...
Golang教程与Gin教程合集,入门到实战
GolangGin框架GormRbac微服务仿小米商城项目实战视频教程Docker Swarm K8s云原生分布式部署 介绍: Go即Golang,是Google公司2009年11月正式对外公开的一门编程语言,它不仅拥有静态编译语言的安全和高性能,而 且又达到了动态语言开…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
