聚类(性能度量)
文章目录
- 聚类(性能度量)
- 外部指标
- 例1
- 内部指标
- 例2
聚类(性能度量)
对数据集 D={x1,x2,...,xm}D=\{x_1,x_2,...,x_m\}D={x1,x2,...,xm} ,假定通过聚类给出的簇划分为 C={C1,C2,...,Ck}C=\{C_1,C_2,...,C_k\}C={C1,C2,...,Ck} ,参考模型给出的簇划分为 C∗={C1∗,C2∗,...,Cs∗}C^*=\{C_1^*,C_2^*,...,C_s^*\}C∗={C1∗,C2∗,...,Cs∗} ,相应的,令 λ\lambdaλ 与 λ∗\lambda^*λ∗ 分别表示与 CCC 和 C∗C^*C∗ 对应的簇标记向量。我们将样本两两配对考虑,定义:
a=∣SS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}b=∣SD∣,SS={(xi,xj)∣λi=λj,λi∗≠λj∗,i<j}c=∣DS∣,SS={(xi,xj)∣λi≠λj,λi∗=λj∗,i<j}d=∣DD∣,SS={(xi,xj)∣λi≠λj,λi∗≠λj∗,i<j}a=\vert SS \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i=\lambda_j,\lambda_i^*=\lambda_j^*,i<j\} \\ b=\vert SD \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i=\lambda_j,\lambda_i^* \neq \lambda_j^*,i<j\} \\ c=\vert DS \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i \neq \lambda_j,\lambda_i^*=\lambda_j^*,i<j\} \\ d=\vert DD \vert,\quad SS=\{(x_i,x_j) \quad| \quad \lambda_i \neq \lambda_j,\lambda_i^* \neq \lambda_j^*,i<j\} a=∣SS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}b=∣SD∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}c=∣DS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}d=∣DD∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j}
其中,集合 SSSSSS 包含了在 CCC 中隶属于相同簇且在 C∗C^*C∗ 中也隶属于相同簇的样本对,…
由于每个样本对 (xi,xj)(i<j)(x_i,x_j)(i<j)(xi,xj)(i<j) 仅能出现在一个集合中,因此有下列式子成立:
a+b+c+d=m(m−1)2a+b+c+d=\frac {m(m-1)} {2} a+b+c+d=2m(m−1)
外部指标
基于以上式子可导出下面这些常用的聚类性能度量外部指标:
- Jaccard系数(Jaccard Coefficient,简称 JC)
JC=aa+b+cJC = \frac {a} {a+b+c} JC=a+b+ca
- FM指数(Fowlkes and Mallows Index,简称 FMI)
FMI=aa+b⋅aa+cFMI = \sqrt{\frac {a} {a+b} \cdot \frac {a} {a+c}} FMI=a+ba⋅a+ca
- Rand指数(Rand Index,简称 RI)
RI=a(a+d)m(m−1)RI = \frac {a(a+d)} {m(m-1)} RI=m(m−1)a(a+d)
显然,上述性能度量的结果值均在 [0,1][0,1][0,1] 区间,值越大越好。
例1
| 聚类 CCC | 参考 C∗C^*C∗ |
|---|---|
| C1:x1,x2,x3C_1:x_1,x_2,x_3C1:x1,x2,x3 | C1∗:x1,x2,x4C_1^*:x_1,x_2,x_4C1∗:x1,x2,x4 |
| C2:x4,x5C_2:x_4,x_5C2:x4,x5 | C2∗:x3,x5C_2^*:x_3,x_5C2∗:x3,x5 |
a=∣SS∣=1(x1,x2)b=∣SD∣=3(x1,x3),(x2,x3),(x4,x5)c=∣DS∣=3(x1,x4),(x2,x4),(x3,x5)d=∣DD∣=3(x1,x5),(x2,x5),(x3,x4)\begin {aligned} a&=\vert SS \vert =1 \quad (x_1,x_2) \\ b&=\vert SD \vert =3 \quad (x_1,x_3),(x_2,x_3),(x_4,x_5) \\ c&=\vert DS \vert =3 \quad (x_1,x_4),(x_2,x_4),(x_3,x_5) \\ d&=\vert DD \vert =3 \quad (x_1,x_5),(x_2,x_5),(x_3,x_4) \end {aligned} abcd=∣SS∣=1(x1,x2)=∣SD∣=3(x1,x3),(x2,x3),(x4,x5)=∣DS∣=3(x1,x4),(x2,x4),(x3,x5)=∣DD∣=3(x1,x5),(x2,x5),(x3,x4)
JC=aa+b+c=11+3+3=17FMI=aa+b⋅aa+c=11+3⋅11+3=14RI=a(a+d)m(m−1)=RI=2(1+3)5(5−1)=25\begin {aligned} JC &= \frac {a} {a+b+c} = \frac {1} {1+3+3} = \frac {1} {7} \\ FMI &= \sqrt{\frac {a} {a+b} \cdot \frac {a} {a+c}} = \sqrt{\frac {1} {1+3} \cdot \frac {1} {1+3}} = \frac {1} {4} \\ RI &= \frac {a(a+d)} {m(m-1)} = RI = \frac {2(1+3)} {5(5-1)} = \frac {2} {5} \end {aligned} JCFMIRI=a+b+ca=1+3+31=71=a+ba⋅a+ca=1+31⋅1+31=41=m(m−1)a(a+d)=RI=5(5−1)2(1+3)=52
内部指标
考虑聚类结果的簇划分为 C={C1,C2,...,Ck}C = \{C_1,C_2,...,C_k\}C={C1,C2,...,Ck} ,定义
avg(C)=2∣C∣(∣C∣−1)∑1≤i<j≤∣C∣dist(xi,xj)avg(C) = \frac {2} {\vert C \vert (\vert C \vert -1)} \sum_{1 \leq i < j \leq \vert C \vert} dist(x_i,x_j) avg(C)=∣C∣(∣C∣−1)21≤i<j≤∣C∣∑dist(xi,xj)
其中,avg(C)avg(C)avg(C) 对应于簇 CCC 内样本间的平均距离,dist(⋅,⋅)dist(\cdot,\cdot)dist(⋅,⋅) 用于计算两个样本之间的距离。
diam(C)=max1≤i<j≤∣C∣dist(xi,xj)diam(C) = max_{1 \leq i < j \leq \vert C \vert} dist(x_i,x_j) diam(C)=max1≤i<j≤∣C∣dist(xi,xj)
diam(C)diam(C)diam(C) 对应于簇 CCC 内样本间的最远距离。
dmin(Ci,Cj)=minxi∈Ci,xj∈Cjdist(xi,xj)d_{min}(C_i,C_j) = min_{x_i \in C_i,x_j \in C_j} dist(x_i,x_j) dmin(Ci,Cj)=minxi∈Ci,xj∈Cjdist(xi,xj)
dmin(Ci,Cj)d_{min}(C_i,C_j)dmin(Ci,Cj) 对应于簇 CiC_iCi 和簇 CjC_jCj 最近样本间的距离。
dcen(Ci,Cj)=dist(μi,μj)d_{cen}(C_i,C_j) = dist(\mu_i,\mu_j) dcen(Ci,Cj)=dist(μi,μj)
dcen(Ci,Cj)d_{cen} (C_i,C_j)dcen(Ci,Cj) 对应于簇 CiC_iCi 和簇 CjC_jCj 中心点间的距离,μ\muμ 代表簇 CCC 的中心点 μ=1∣C∣∑1≤i≤∣C∣xi\mu = \frac {1} {\vert C \vert} \sum_{1 \leq i \leq \vert C \vert} x_iμ=∣C∣1∑1≤i≤∣C∣xi 。
基于以上式子可导出下面这些常用的聚类性能度量内部指标:
- DB指数(Davies-Bouldin Index,简称 DBI)
DBI=1k∑i=1kmaxj≠i(avg(Ci)+avg(Cj)dcen(Ci,Cj))DBI = \frac {1} {k} \sum_{i=1}^{k} \max \limits_{j \neq i}(\frac {avg(C_i) + avg(C_j)} {d_{cen}(C_i,C_j)}) DBI=k1i=1∑kj=imax(dcen(Ci,Cj)avg(Ci)+avg(Cj))
- Dunn指数(Dunn Index,简称DI)
DI=min1≤i≤kminj≠i(dmin(Ci,Cj)max1≤l≤kdiam(Cl))DI = \min \limits_{1 \leq i \leq k} \min \limits_{j \neq i}(\frac {d_{min}(C_i,C_j)} {max_{1 \leq l \leq k} diam(C_l)}) DI=1≤i≤kminj=imin(max1≤l≤kdiam(Cl)dmin(Ci,Cj))
显然,DBIDBIDBI 的值越小越好,而 DIDIDI 则相反,值越大越好。
例2
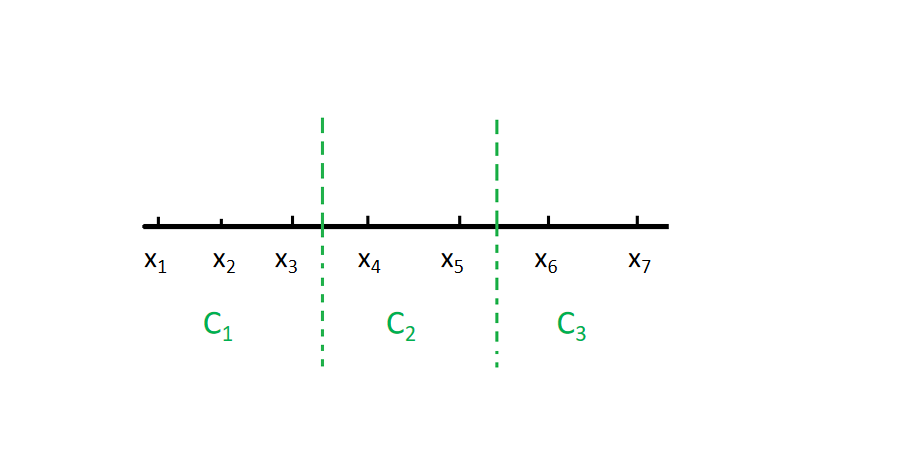
avg(C1)=23(3−1)⋅(∣x1−x2∣+∣x1−x3∣+∣x2−x3∣)avg(C2)=22(2−1)⋅(∣x4−x5∣)avg(C3)=22(2−1)⋅(∣x6−x7∣)\begin {aligned} avg(C_1) &= \frac {2} {3 (3 -1)} \cdot (\vert x_1-x_2 \vert + \vert x_1 - x_3 \vert + \vert x_2 - x_3 \vert) \\ avg(C_2) &= \frac {2} {2 (2 -1)} \cdot (\vert x_4-x_5 \vert) \\ avg(C_3) &= \frac {2} {2 (2 -1)} \cdot (\vert x_6-x_7 \vert) \end {aligned} avg(C1)avg(C2)avg(C3)=3(3−1)2⋅(∣x1−x2∣+∣x1−x3∣+∣x2−x3∣)=2(2−1)2⋅(∣x4−x5∣)=2(2−1)2⋅(∣x6−x7∣)
diam(C1)=∣x1−x3∣diam(C2)=∣x4−x5∣diam(C3)=∣x6−x7∣diam(C_1) = \vert x_1 - x_3 \vert \\ diam(C_2) = \vert x_4 - x_5 \vert \\ diam(C_3) = \vert x_6 - x_7 \vert diam(C1)=∣x1−x3∣diam(C2)=∣x4−x5∣diam(C3)=∣x6−x7∣
dmin(C1,C2)=∣x3−x4∣dmin(C2,C3)=∣x5−x6∣dmin(C1,C3)=∣x3−x6∣d_{min}(C_1,C_2) = \vert x_3 - x_4 \vert \\ d_{min}(C_2,C_3) = \vert x_5 - x_6 \vert \\ d_{min}(C_1,C_3) = \vert x_3 - x_6 \vert dmin(C1,C2)=∣x3−x4∣dmin(C2,C3)=∣x5−x6∣dmin(C1,C3)=∣x3−x6∣
μ1=x1+x2+x33μ2=x4+x52μ3=x6+x72\mu_1 = \frac {x_1 + x_2 + x_3} {3} \quad \mu_2 = \frac {x_4 + x_5} {2} \quad \mu_3 = \frac {x_6 + x_7} {2} μ1=3x1+x2+x3μ2=2x4+x5μ3=2x6+x7
dcen(C1,C2)=∣μ1−μ2∣dcen(C2,C3)=∣μ2−μ3∣dcen(C1,C3)=∣μ1−μ3∣d_{cen}(C_1,C_2) = \vert \mu_1-\mu_2 \vert \\ d_{cen}(C_2,C_3) = \vert \mu_2-\mu_3 \vert \\ d_{cen}(C_1,C_3) = \vert \mu_1-\mu_3 \vert dcen(C1,C2)=∣μ1−μ2∣dcen(C2,C3)=∣μ2−μ3∣dcen(C1,C3)=∣μ1−μ3∣
相关文章:
聚类(性能度量)
文章目录聚类(性能度量)外部指标例1内部指标例2聚类(性能度量) 对数据集 D{x1,x2,...,xm}D\{x_1,x_2,...,x_m\}D{x1,x2,...,xm} ,假定通过聚类给出的簇划分为 C{C1,C2,...,Ck}C\{C_1,C_2,...,C_k\}C{C1,C2,…...

GPT-4——比GPT-3强100倍
GPT-4——比GPT-3强100倍 当前世界上最强大的人工智能系统当属ChatGPT。推出2个月用户数就突破1亿。ChatGPT是当下最炙手可热的话题,科技圈几乎人人都在讨论。这边ChatGPT的热度还在不断攀升,另一边来自《纽约时报》的最新报道称ChatGPT即将被自家超越&…...
echart中x轴数据过多时展示不全
项目中遇到需要展示一些柱状图,之前做相关功能时,横坐标x轴一直用的是时间,所以没有注意到这个问题。 如下图所示: 当x轴显示的是”人名“这种类型的值的时候,这种显示情况就有问题了,这样就不会知道&…...

关于GIS原理的实际分析应用题的一些解法
话不多说,看题.01 公园选址问题1题目请写出利用GIS技术进行公园选址的空间操作步骤。其中公园选址条件:1)为了安静舒适,要求该园区离主要公路1公里以外,且交通方便,离主要公路3公里以内。2)公园最好依附在大…...

混合精度训练,FP16加速训练,降低内存消耗
计算机中的浮点数表示,按照IEEE754可以分为三种,分别是半精度浮点数、单精度浮点数和双精度浮点数。三种格式的浮点数因占用的存储位数不同,能够表示的数据精度也不同。 Signed bit用于控制浮点数的正负,0表示正数,1表…...

每天五分钟机器学习:新的大规模的机器学习机制——在线学习机制
本文重点 本节课程我们将学习一种新的大规模的机器学习机制--在线学习机制。在线学习机制让我们可以模型化问题。在线学习算法指的是对数据流进行学习而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流,对于每一个用户,网站希望能在不将数据存储到数据库中便顺…...
计算机组成原理错题
静态RAM(SRAM)和动态RAM(DRAM)的基本电路图不同,因此可以通过观察存储器的基本电路图来判断它属于哪一类。 静态RAM的基本电路图包括一个存储单元和一个数据选择器。每个存储单元由一个触发器(flip-flop&a…...

数学基础整理
收纳一些天天忘的结论qwq 线性求逆元 invi(p−pi)invpmodiinv_i(p-\dfrac{p}{i})\times inv_{p\bmod i}invi(p−ip)invpmodi 卡特兰数 组合数公式:HnC2nn−C2nn−1H_nC_{2n}^n-C_{2n}^{n-1}HnC2nn−C2nn−1 递推式:HnHn−1(4n−2)n1H_n\d…...
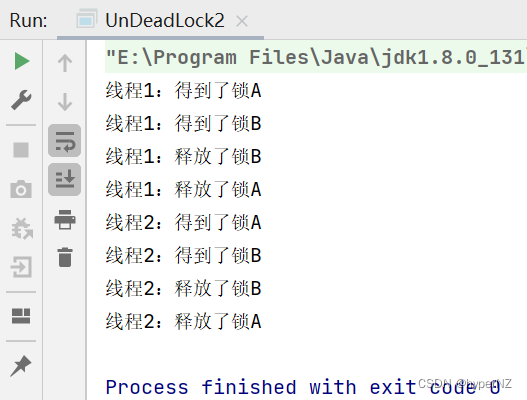
JavaWeb11-死锁
目录 1.死锁定义 1.1.代码演示 1.2.使用jconsole/jvisualvm/jmc查看死锁 ①使用jconsole:最简单。 ②使用jvisualvm:(Java虚拟机)更方便,更直观,更智能,更高级,是合适的选择。 …...
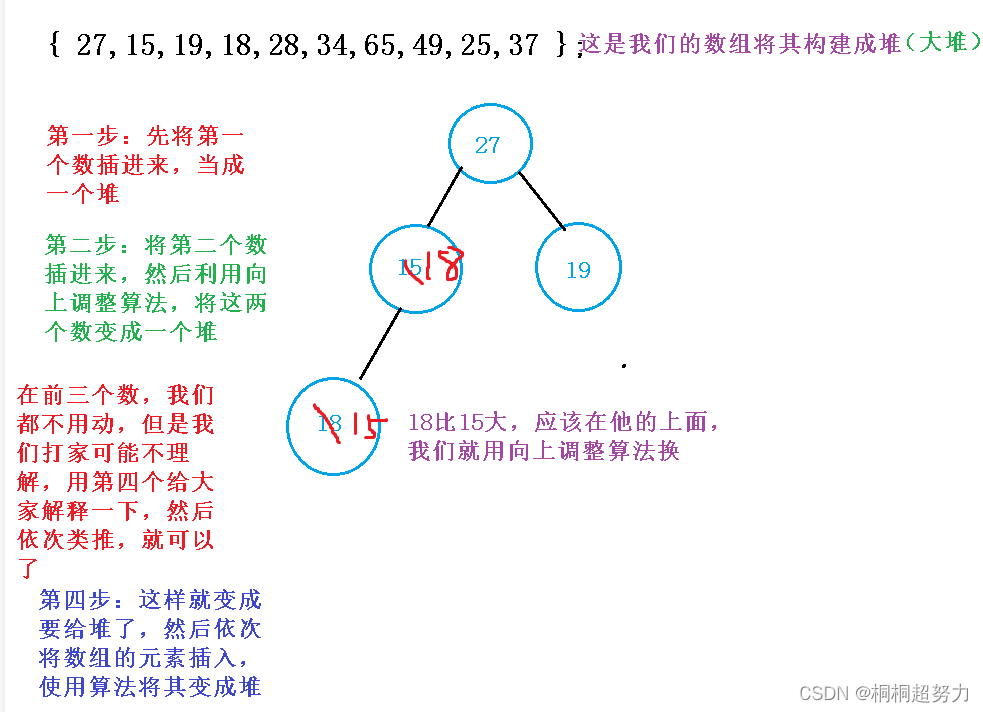
堆的概念和结构以及堆排序
前言 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,…...
【Linux学习笔记】1.Linux 简介及安装
前言 本章介绍Linux及其安装方法。 Linux 简介 Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多…...

代码练习2~
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。def …...

微信小程序 之 云开发
一、概念1. 传统开发模式2. 新开发模式 ( 云开发模式 )3. 传统、云开发的模式对比4. 传统、云开发的项目流程对比5. 云开发的定位1. 个人的项目或者想法,不想开发服务器,直接使用云开发2. 某些公司的小程序项目是使用云开发的,但是不多&#…...

程序员的三门课,学习成长笔记
最近是有了解到一本好书,叫做程序员的三门课在这本书的内容当中我也确实汲取到了很多前辈能够传达出来的很多关于程序员职业规划以及成长路线上的见解,令我受益匪浅,故此想要把阅读完的每一章节结合自己的工作经验做一个精细化的小结…...

[技术经理]01 程序员最优的成长之路是什么?
00前言 谈起程序员的职业规划,针对大部分的职场人士,最优的成长之路应该是走技术管理路线,而不是走技术专家路线。 01关键的一步 中国自古就有“学而优则仕”的传统,发展到今天,在我们的现代企业里面,尤…...
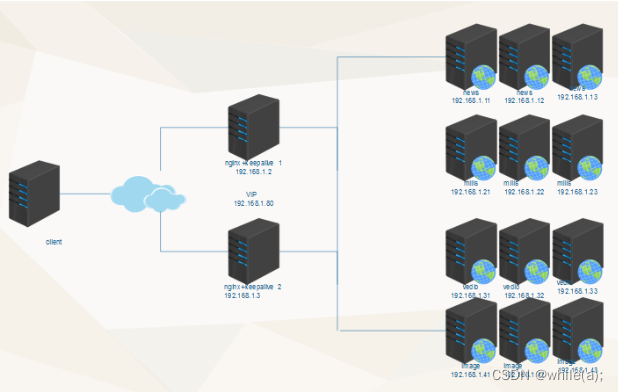
linux集群技术(三)--七层负载均衡-nginx
nginx特点nginx优势、缺点生产架构nginx 7层负载均衡语法示例nginx负载均衡算法测试案例生产案例 1.nginx特点 1. 功能强大,性能卓越,运行稳定。 2. 配置简单灵活。 3. 能够自动剔除工作不正常的后端服务器。 4. 上传文件使用异步模式。client---nginx---web1 web2 web3 lvs同…...
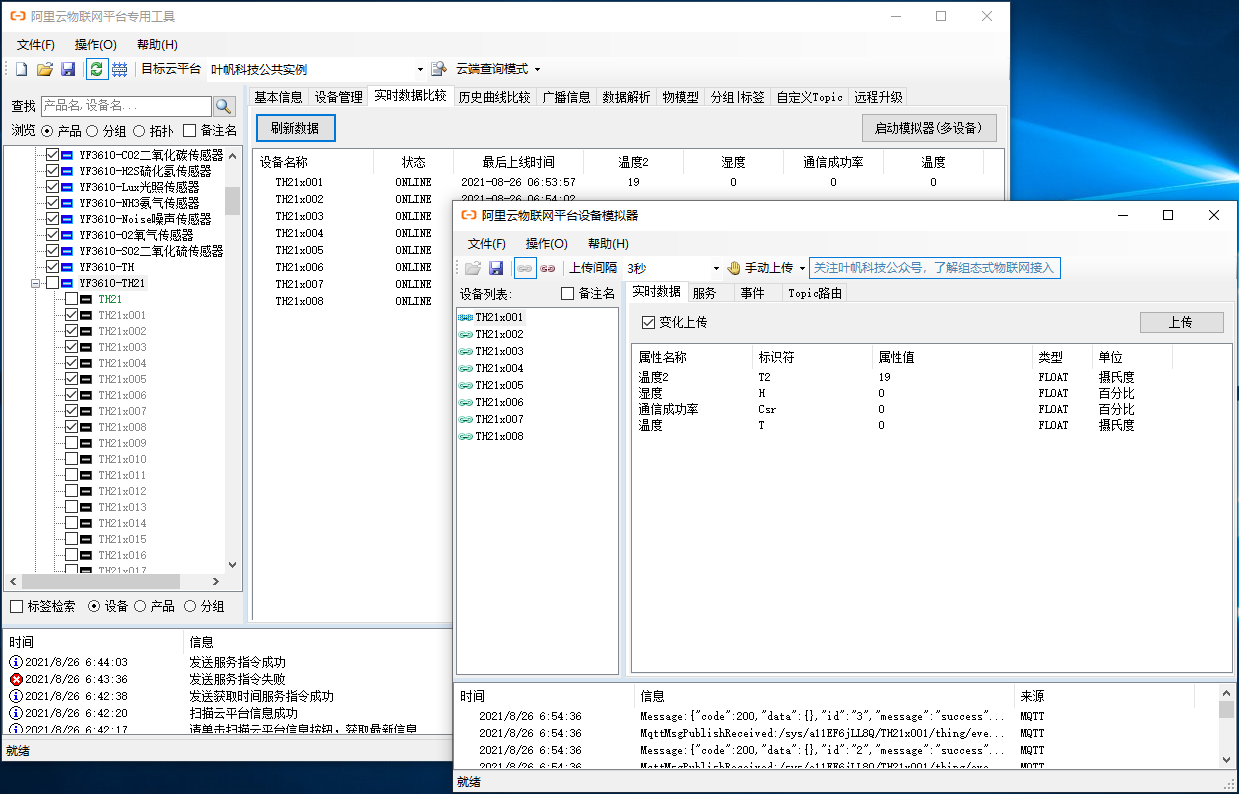
阿里云物联网平台设备模拟器
在使用阿里云物联网平台过程中,如果开始调试没有实际的物理设备,可以考虑在阿里云物联网平台使用官方自带的模拟器进行调试。不过也可以通过叶帆科技开发的阿里云物联网平台设备模拟器AliIoTSimulator进行调试,AliIoTSimulator可以独立运行&a…...
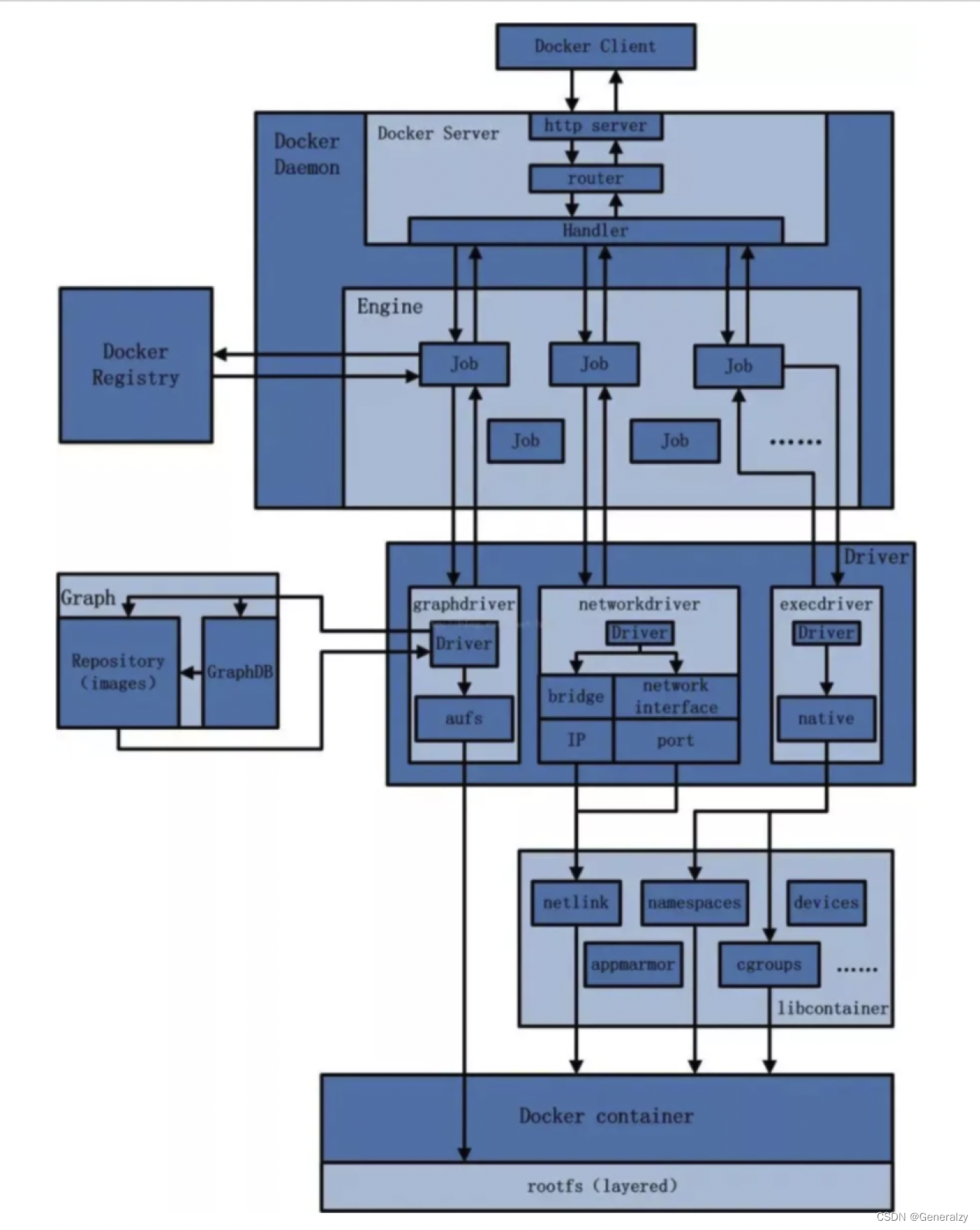
docker全解
目录说明docker简介为什么是docker容器与虚拟机比较容器发展简史传统虚拟机技术容器虚拟化技术docker能干什么带来技术职级的变化开发/运维(Devops)新一代开发工程师Docker应用场景why docker?docker的优势docker和dockerHub官网Docker安装CentOS Docker…...
Vue3 基础
Vue3 基础 概述 Vue (发音为 /vjuː/,类似 view) 是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS 和 JavaScript 构建,并提供了一套声明式的、组件化的编程模型,帮助你高效地开发用户界面。无论是简单还是复杂的界面&…...
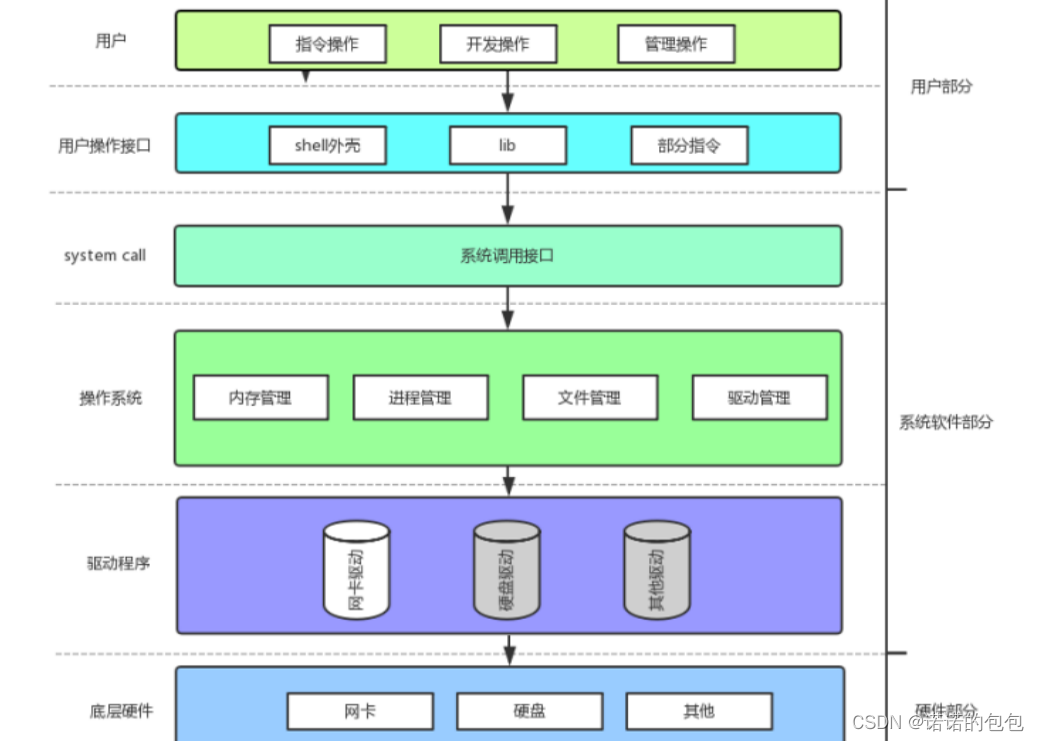
【Linux】冯.诺依曼体系结构与操作系统
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹冯.诺依曼体系结构什么是冯诺依曼体系结构?我们如今的计算机比如笔记本,或者是服务器,基本上都遵循冯诺依曼体系结构…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
