模拟实现链式二叉树及其结构学习——【数据结构】

W...Y的主页 😊
代码仓库分享 💕
之前我们实现了用顺序表完成二叉树(也就是堆),顺序二叉树的实际作用就是解决堆排序以及Topk问题。
今天我们要学习的内容是链式二叉树,并且实现链式二叉树,这篇博客与递归息息相关!
目录
链式存储
二叉树链式结构的实现
链式二叉树的快速创建
二叉树的遍历
前序、中序以及后序遍历
前序遍历的实现
中序遍历的实现
后序遍历实现
节点个数以及高度
总结点个数
叶子节点个数
第k层节点个数
整个代码模板以及验证
链式存储
什么是链式存储,就是用链来指示元素的逻辑关系。链式结构又分为二叉链和三叉链,而我们今天学习的是二叉链表,又称链式二叉树。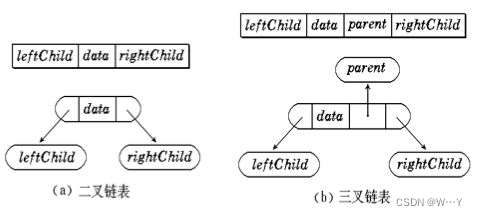
我们一般用链表来表示一棵二叉树,通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}对于链式二叉树,我们与其他前面的链表、顺序表、堆……数据结构有所不同,我们针对这一块并不是增删查改,为什么呢?
因为链式二叉树的存储方式,就是把每一个节点封装在结构体中然后进行链接, 而我们进行增删查改没有必要在这么复杂的结构中实现,当我有每个节点的左右指针时,我可以随心所欲,在哪里都可以进行插入删除。如果非得使用增删查改,我们就可以使用简单一些的数据结构进行。
所以我们学习链式二叉树是为了给我们后面的高级数据结构AVL、红黑树打基础的。所以我们也要认真学!!!
二叉树链式结构的实现
链式二叉树的快速创建
我们为了快速实现链式二叉树,从中感受到链式二叉树的结构,我们快速手动生成一个链式二叉树。
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}
int main(void)
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return 0;
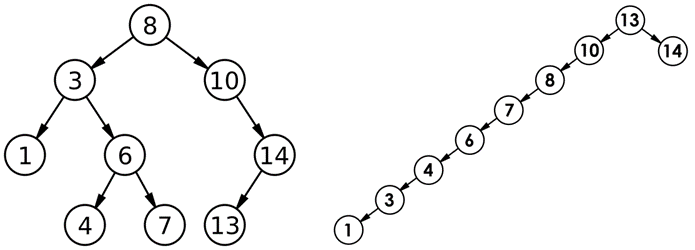
}我们创建了链式二叉树的基本结构,左指针右指针以及存储的值,然后开辟空间将里面的所有内容初始化。在main函数中手动插入了1、2、3、4、5、6封装在结构体中,然后依照下图进行链接快速得到一个链式二叉树。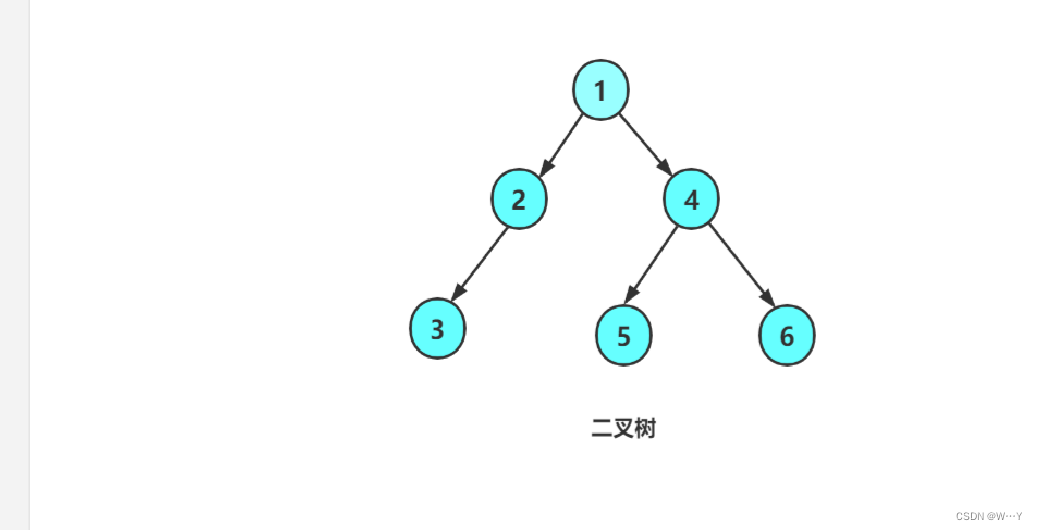
下面依照创建完成的链式二叉树继续学习。
二叉树的遍历
前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
前序遍历的实现
针对前序遍历,我们记住先访问左树,再访问根,最后再访问右树。我们可以先手动遍历一遍,将一颗大树分解成三部分(左树、根、右树),再将左树看作树继续分成左树右树与根,右数也一样,将其一直进行分解,直到左右树为空为止即可停止。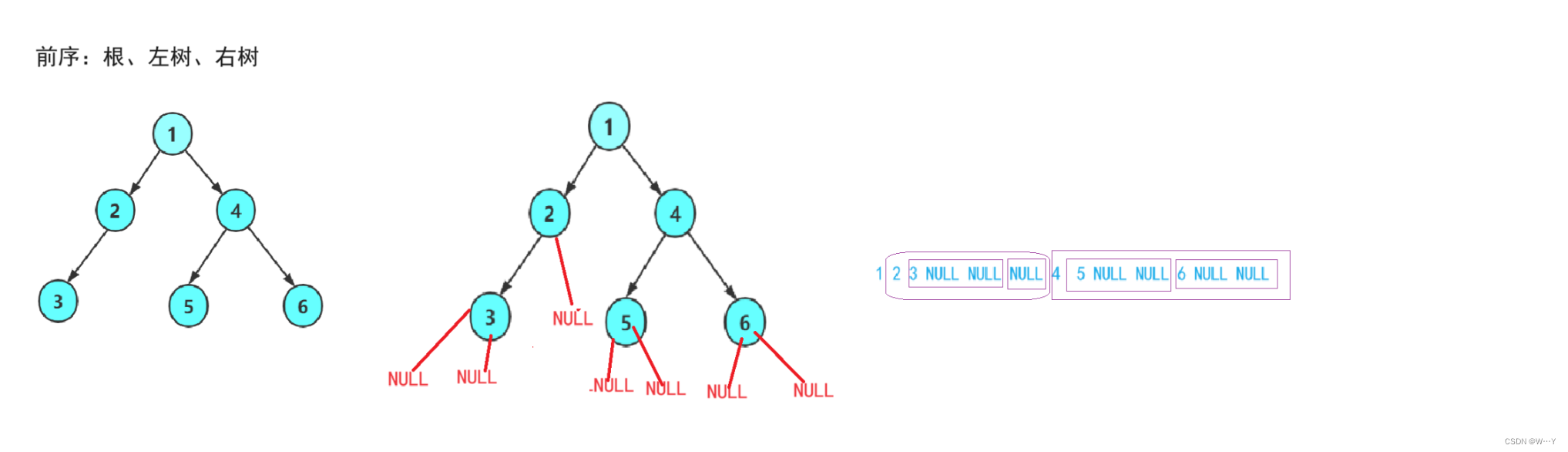
// 二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
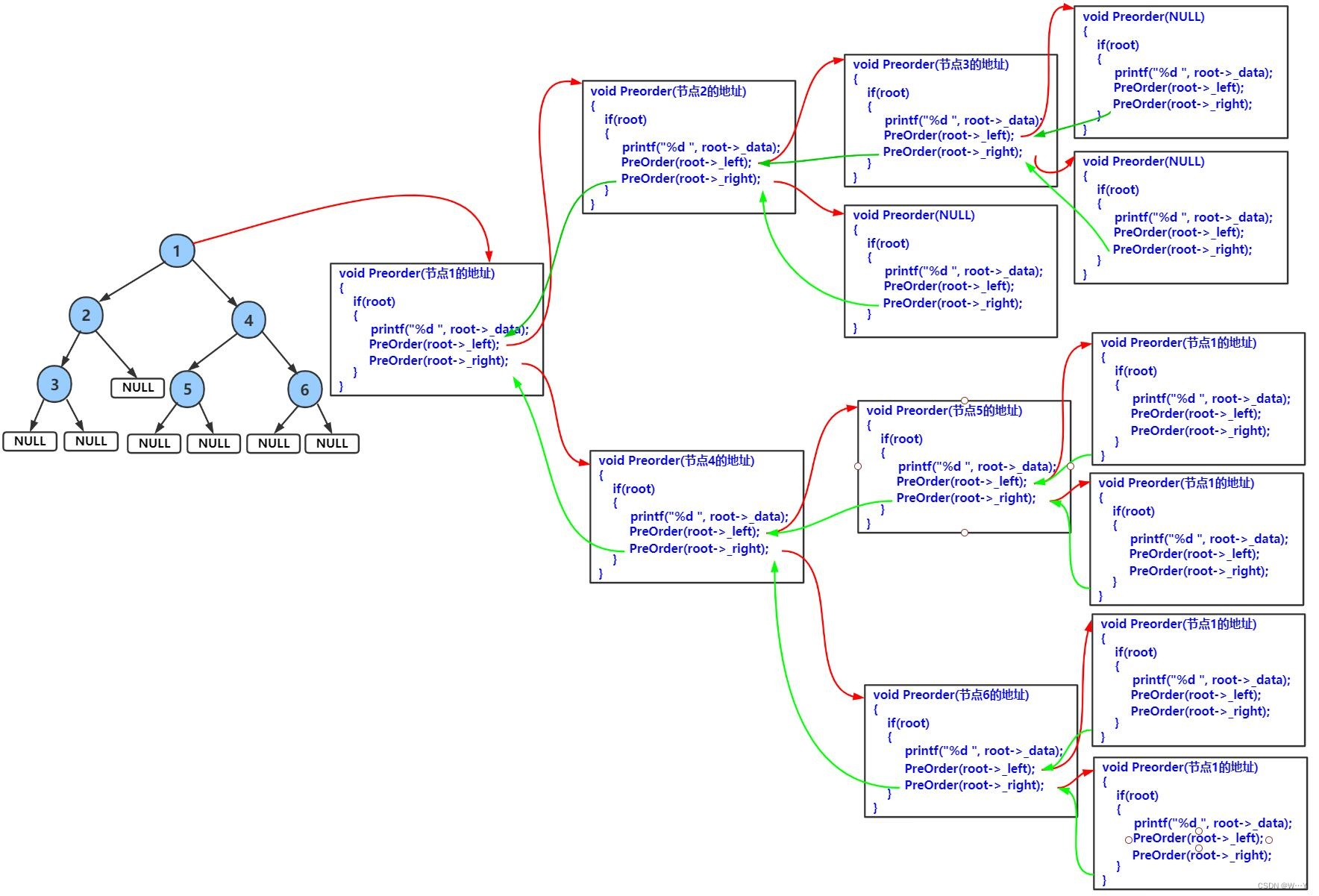
}在前序遍历中,我们使用递归进行。如果root为NULL证明树为空,直接返回即可。当进入下面代码时,前序遵循的是根、左树、右树。所以我们先将根打印出来,然后遍历左树。当进入左树递归时,root->left进入左树,那根的左子节点就变成了左树的根,打印出来继续递归,依次类推。而右树也是一样的,将左树遍历完后,我们将递归右数,先将左树递归的所有函数销毁,进入root->right中进行递归,根的右子节点成为右树的根,打印出进行递归,一直遵循根、左树、右树进行。
递归图解如下: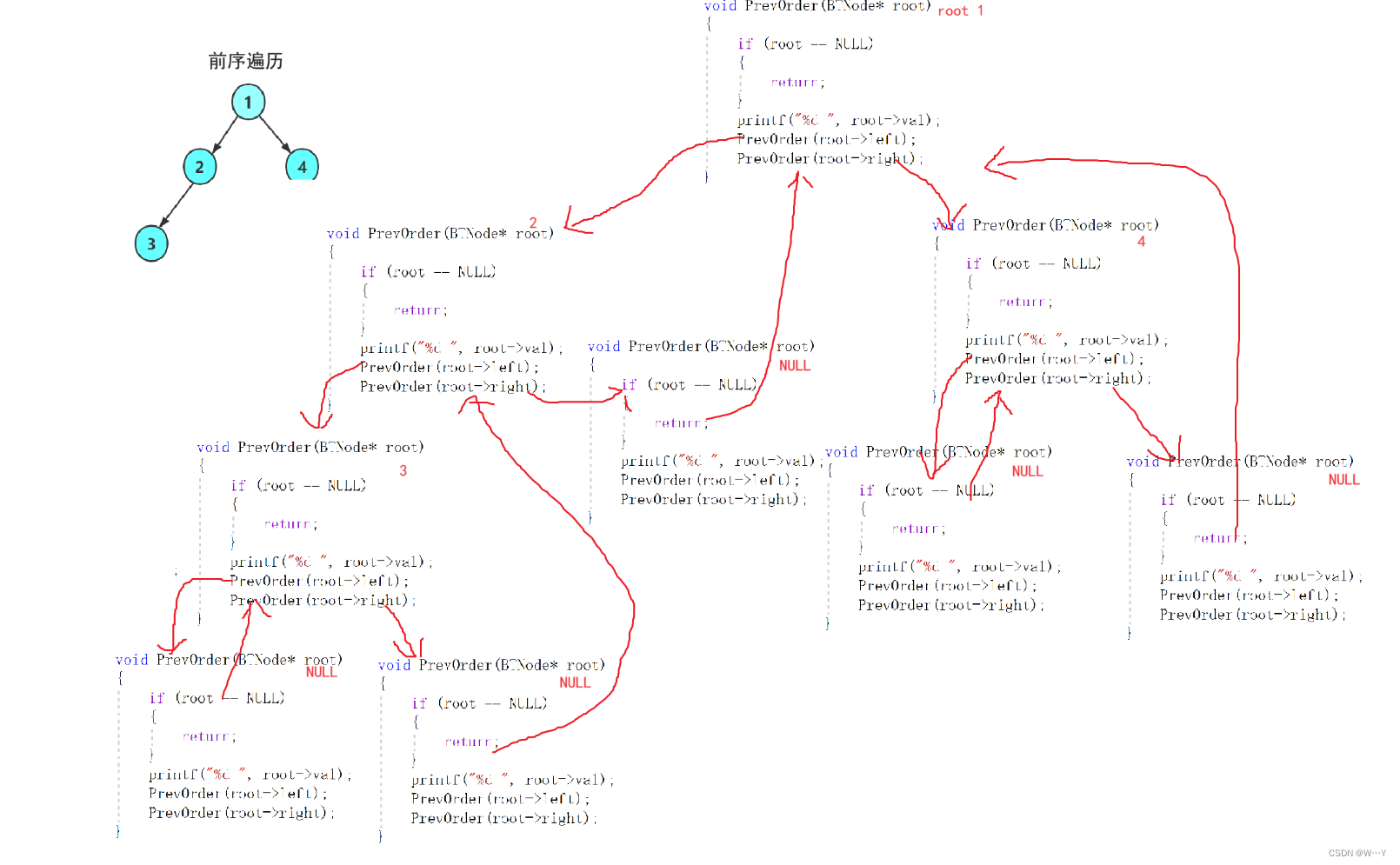
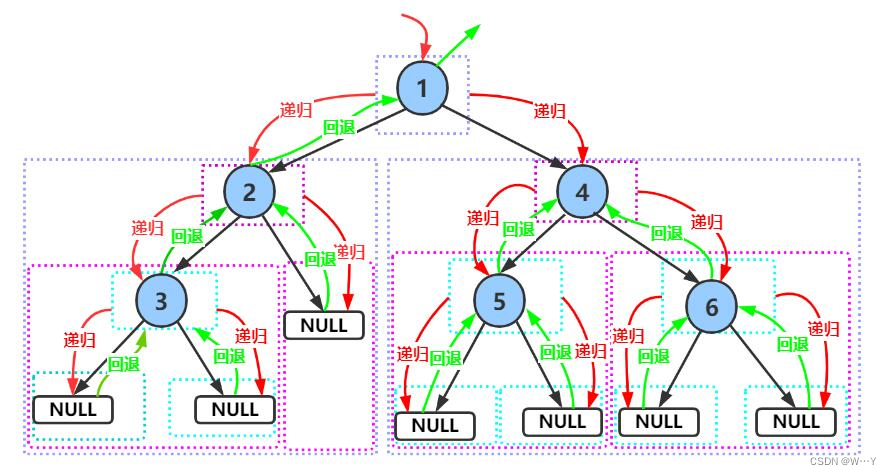 虽然代码非常简洁,但是理解起来不太容易,我们不能只记住代码如何写,应该理解其中的原理才行。
虽然代码非常简洁,但是理解起来不太容易,我们不能只记住代码如何写,应该理解其中的原理才行。
中序遍历的实现
只要我们理解了前序遍历,那么中序后序都是非常简单的存在。只需记住:左树、根、右树,然后写出递归即可
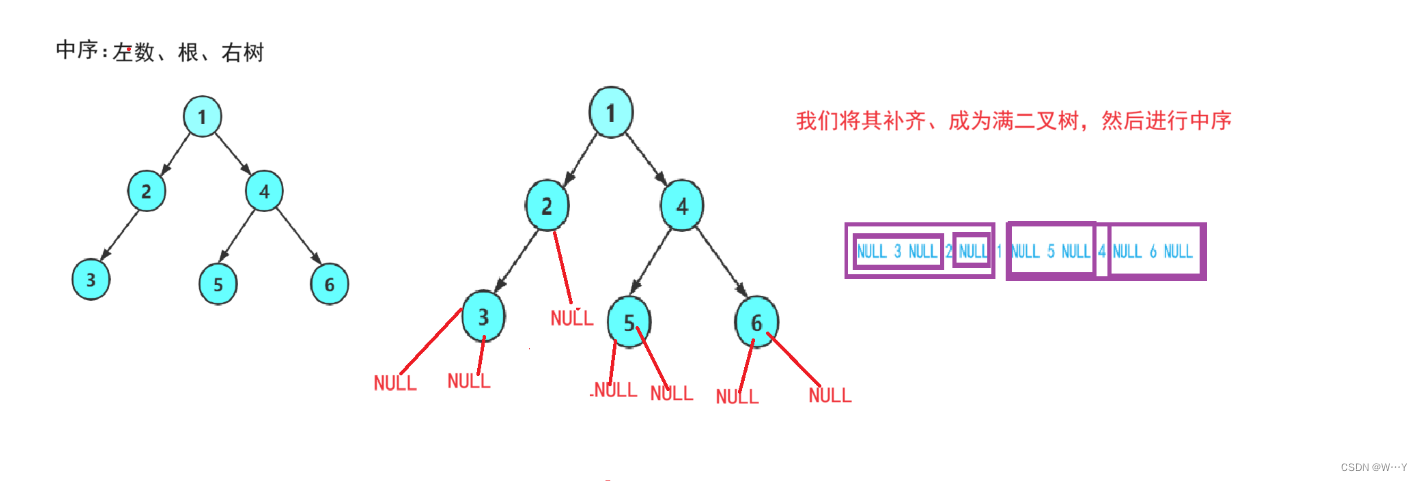
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}有没有发现这串代码与前序遍历非常相似,只是将两行代码交换位置就可以实现。我们先将左树的内容递归完然后打印,再打印根的,最后再打印右树的即可。可以参考前置遍历进行推理。
这里如果实在理解不了的可以认为调用InOrder(root->left)是遍历打印左树,printf是打印根,而调用递归InOrder(root->right)是为了遍历打印右树。
后序遍历实现
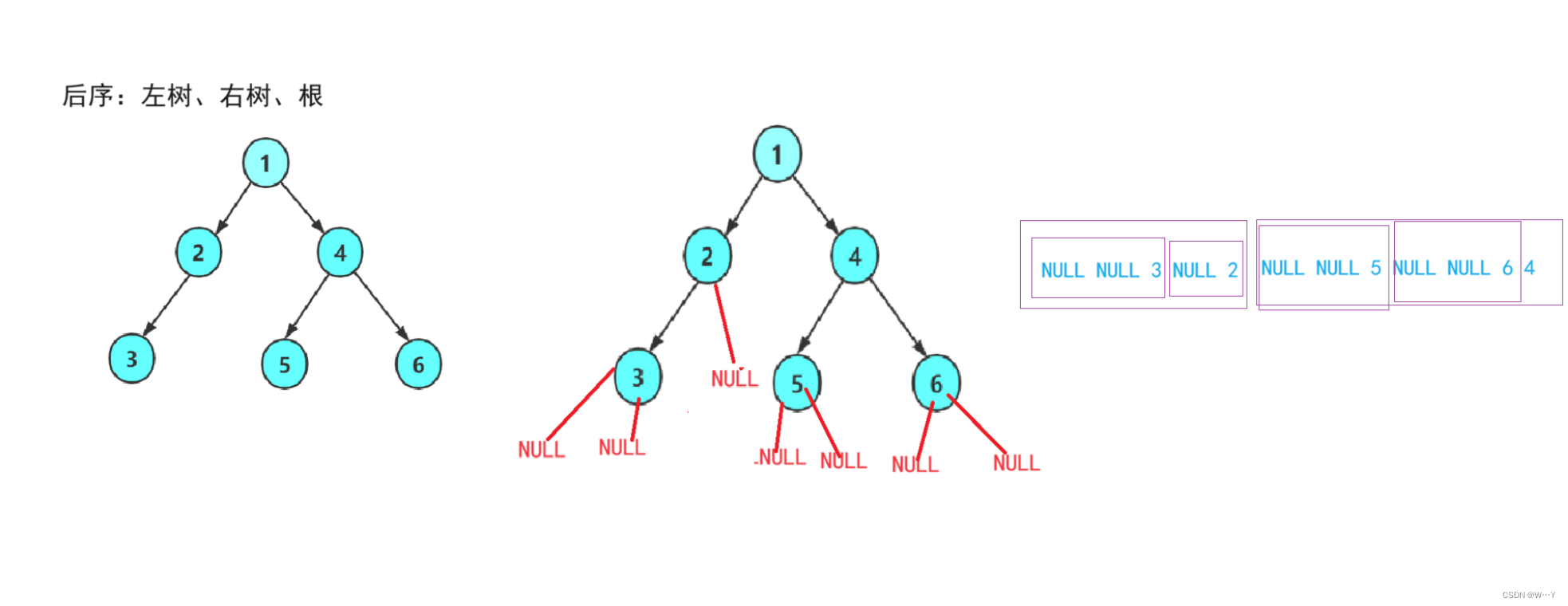
我相信大家已经知道函数怎么写了,那我就直接给模板:
void PostOrder(BTNode* root)
{if (root == NULL){return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}下面我们更进一步的学习链式二叉树的结构,上强度!!!
节点个数以及高度
总结点个数
我们需要建立一个函数,求出整个二叉树所有的节点个数。
有人一定会想直接全部遍历一遍然后创建一个全局变量用来统计个数就可以了。没错这个方法是可行的,我们刚才说的二叉树的遍历,然后在这里用一遍不就拿下来了。
int size = 0;
int TreeSize(BTNode* root)
{if (root == NULL)return 0;else++size;TreeSize(root->left);TreeSize(root->right);return size;
}我们直接遍历整棵树,先遍历左树、再遍历右数,每遍历一个节点size++即可。
但是这个函数有一个极大的缺点,当我们使用函数时,我们可以在任意一个位置去调用,全局变量是存储在静态区的,不会随着函数的结束而销毁,当我们调用过一次后, 再一次去调用此函数,如果没有及时将size归零,结果将会累加起来成为错误的结果。
我们应该优化一下程序:
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}直接使用递归,将左右子树包含在返回值中,我们在后面加上1,如果递归成功将+1,然后返回最后递归之和。
我们可以做个比喻:在一个大学中校长想要统计全校的人数,校长不可能亲自挨家挨户访问查人,它会通知每个院的院长,然后院长通知每个系的系主任,由系主任通知导员,最后由导员通知每个班的班长来统计人数。一级一级的下放任务。而这个递归也是如此,统计总节点个数就是一级一级下方给各个节点计数。
叶子节点个数
需要求出链式二叉树的叶子节点个数,叶节点或终端节点:度为0的节点称为叶节点;
大致原理都是一样的,只是条件不同。我们需要叶子节点就必须是度为0的节点,所以一个节点的root->right == NULL && root->left == NULL 这是必要条件,然后我们就应该去遍历二叉树的左子树与右子树去寻找满足条件的节点。最后求出左右子树的叶子节点之和即可。
代码实现:
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->right == NULL && root->left == NULL)return 1;return TreeLeafSize(root->right) + TreeLeafSize(root->left);
}第k层节点个数
当我们需要某一层的节点个数,我们也需要创建一个函数来进行,那我们应该怎么弄呢?
还是一级一级去派遣,假设我们需要第三层的节点个数,当我们刚进入在第一层时,我们距离目标层数还有两层之差,当我们遍历到第二层时,我们距离目标还有一层,当我们进入目标层后我们就要进行遍历节点, 统计出左右子树k层节点之和返回即可。
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0; }if (k == 1){return 1;}return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}需要注意的是我们先得使用assert进行断言,防止树为空。
整个代码模板以及验证
下面是增章全部代码以及测试用例:
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;int val;
}BTNode;BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}void PrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
void PostOrder(BTNode* root)
{if (root == NULL){return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
//总节点个数
//int TreeSize(BTNode* root)
//{
// static int size = 0;
// if (root == NULL)
// return 0;
// else
// ++size;
// TreeSize(root->left);
// TreeSize(root->right);
// return size;
//}
//int size = 0;
//int TreeSize(BTNode* root)
//{
// if (root == NULL)
// return 0;
// else
// ++size;
// TreeSize(root->left);
// TreeSize(root->right);
// return size;
//}
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->right == NULL && root->left == NULL)return 1;return TreeLeafSize(root->right) + TreeLeafSize(root->left);
}
//第k层节点个数
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0; }if (k == 1){return 1;}return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}int main(void)
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;PrevOrder(node1);printf("\n");InOrder(node1);printf("\n");PostOrder(node1);printf("\n%d", TreeSize(node1));printf("\n%d", TreeSize(node1));printf("\n%d", TreeLeafSize(node1));printf("\n%d", TreeKLevel(node1, 2));return 0;
}代码运行结果如下:

运行结果分别为前置遍历、中序遍历、后序遍历、总节点个数(两次)、叶子节点个数、第二层节点个数
参考下图均正确!!!
以上就是本次博客的全部内容,希望可以帮助到大家!!!支持博主的一键三连一下,谢谢大家❤️
相关文章:

模拟实现链式二叉树及其结构学习——【数据结构】
W...Y的主页 😊 代码仓库分享 💕 之前我们实现了用顺序表完成二叉树(也就是堆),顺序二叉树的实际作用就是解决堆排序以及Topk问题。 今天我们要学习的内容是链式二叉树,并且实现链式二叉树,这篇博客与递归息息相关&a…...

基于go版本的LoraWAN Server 的470MHz频段的设置
一、参考链接 如果您已经基于最新版本的LoraWAN Server(go 版本)的环境,搭建好了服务器的环境,但尚未进行参数设置(此处以470MHz频段设置为例),可以参考如下链接进行设置: LoraWAN…...

C与C++的函数相互调用
无法直接调用原因: C 和 C 的函数可以相互调用,但需要一些特殊的注意事项,因为它们有不同的编译和链接规则以及一些语法差异。 链接规则: C 语言的链接器通常使用 C 标准的函数命名和调用约定,而 C 链接器使用 C 的函数…...
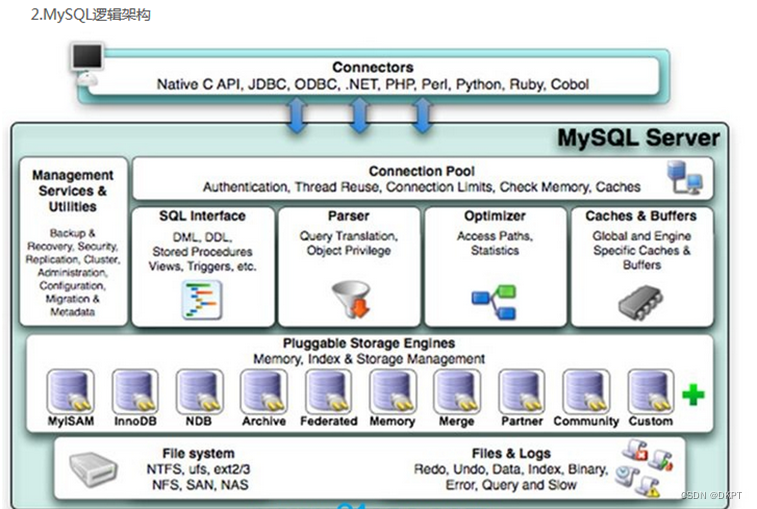
MySQL架构介绍与说明
1、MySQL架构介绍 和其它数据库相比,MySQL有点与众不同,它的架构可以在多种不同场景中应用并发挥良好作用。主要体现在存储引擎的架构上, 插件式的存储引擎架构将查询处理和其它的系统任务以及数据的存储提取相分离。这种架构可以根据业务的…...
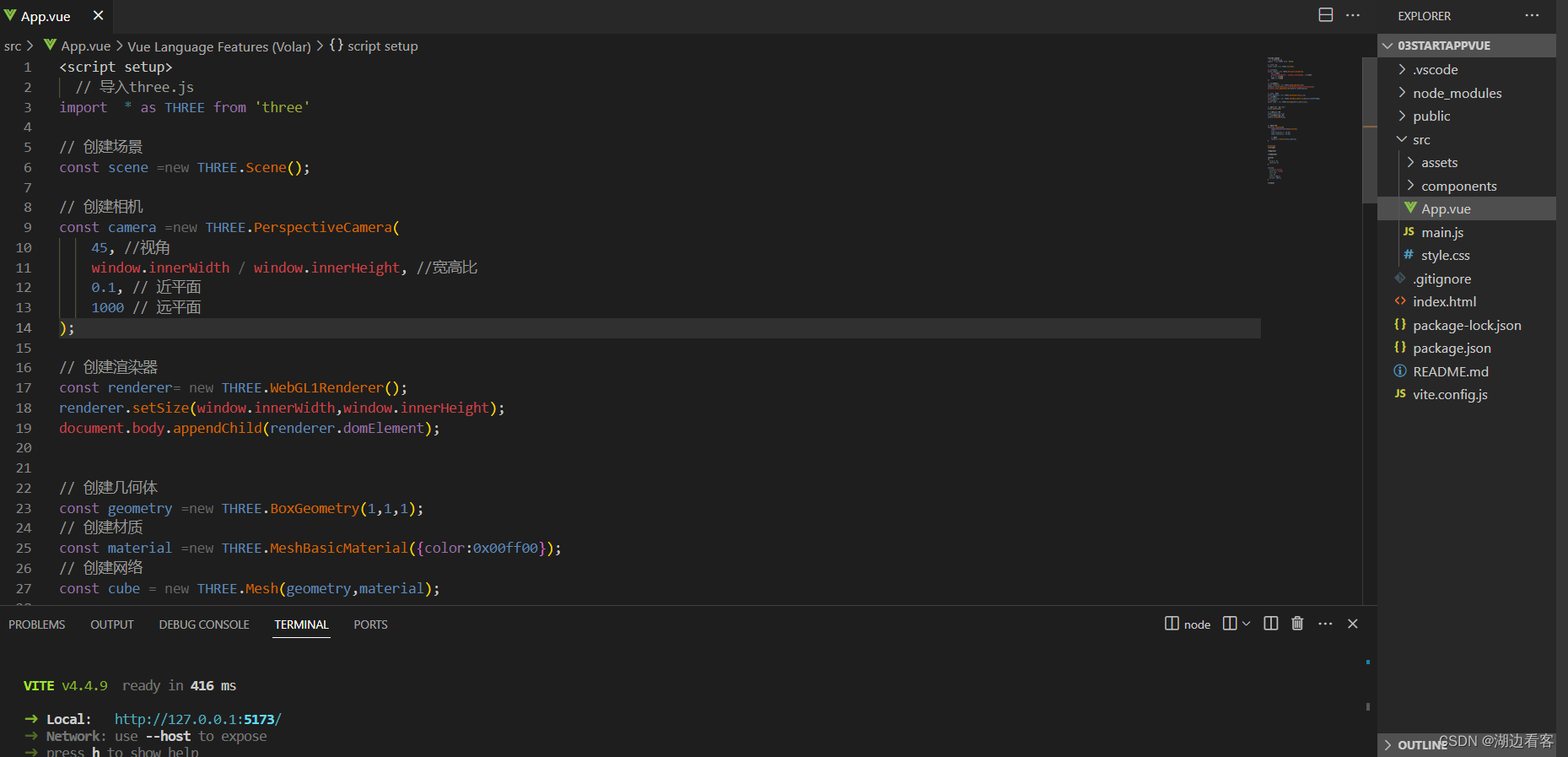
three3D的vite+vue版本基础代码
自己稍微处理一下目录结构 <script setup>// 导入three.js import * as THREE from three// 创建场景 const scene new THREE.Scene();// 创建相机 const camera new THREE.PerspectiveCamera(45, //视角window.innerWidth / window.innerHeight, //宽高比0.1, // 近平…...

实现按钮悬停动画
知识点与技巧 伪元素 使用伪元素来作为按钮悬停效果动画展示的元素 z-index 的使用技巧 使用z-index属性来控制按钮和伪元素的层次关系 transform、transition 复习 使用transform、transition两个属性来实现动画的展示 按钮边框动画 切换效果 核心代码 .btn.btn-border-…...
【C++】深拷贝和浅拷贝 ② ( 默认拷贝构造函数是浅拷贝 | 代码示例 - 浅拷贝造成的问题 )
文章目录 一、默认拷贝构造函数是浅拷贝1、默认拷贝构造函数2、默认拷贝构造函数是浅拷贝机制 二、代码示例 - 浅拷贝造成的问题 一、默认拷贝构造函数是浅拷贝 1、默认拷贝构造函数 如果 C 类中 没有定义拷贝构造函数 , C 编译器会自动为该类提供一个 " 默认的拷贝构造函…...
【Selenium】webdriver.ChromeOptions()官方文档参数
Google官方Chrome文档,在此记录一下 Chrome Flags for Tooling Many tools maintain a list of runtime flags for Chrome to configure the environment. This file is an attempt to document all chrome flags that are relevant to tools, automation, benchm…...
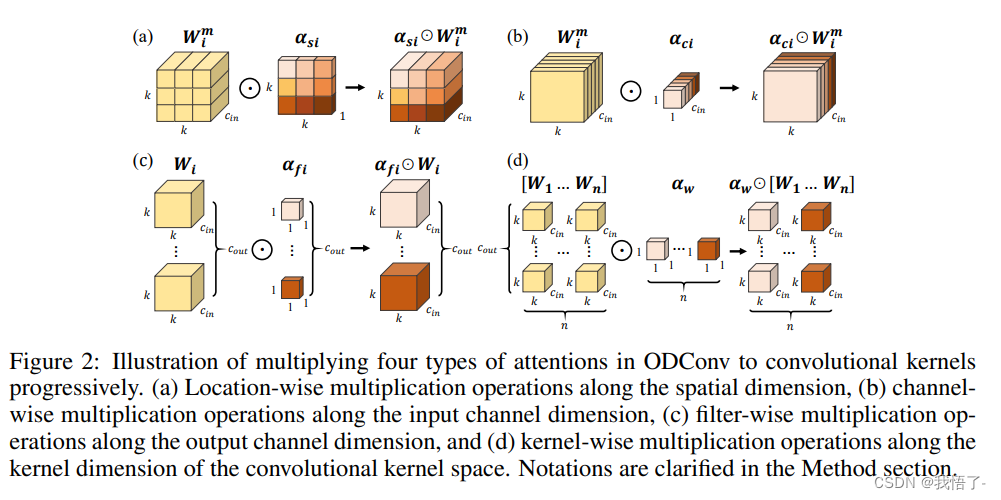
pytorch代码实现之动态卷积模块ODConv
ODConv动态卷积模块 ODConv可以视作CondConv的延续,将CondConv中一个维度上的动态特性进行了扩展,同时了考虑了空域、输入通道、输出通道等维度上的动态性,故称之为全维度动态卷积。ODConv通过并行策略采用多维注意力机制沿核空间的四个维度…...

动态规划:子序列问题(C++)
动态规划:子序列问题 前言子序列问题1.最长递增子序列(中等)2.摆动序列(中等)3.最长递增子序列的个数(中等)4.最长数对链(中等)5.最长定差子序列(中等&#x…...
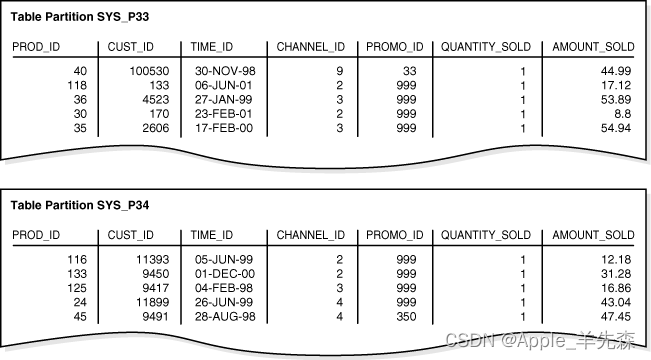
ORACLE的分区(一)
目录 一、分区概念 二、表分区的优点 三、分区策略 一、分区概念 随着时间的发展,一个表的数据会越来越多,当数据量增大的时候我们一般采取建立索引优化索引的方式提高查询速度,但是数据量再次增大即使是索引也无法提高速度,这时…...
【数据结构】C++实现二叉搜索树
二叉搜索树的概念 二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。若它的右子树不为空,则右子树上所有结点的值都大于根结…...

Python中Mock和Patch的区别
前言: 嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 在测试并行开发(TPD)中,代码开发是第一位的。 尽管如此,我们还是要写出开发的测试,…...
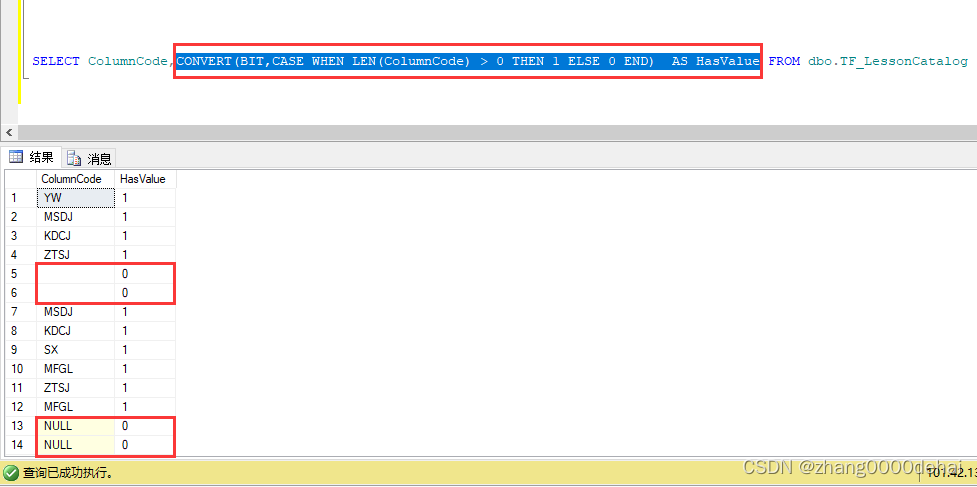
sql server 查询某个字段是否有值 返回bool类型
sql server 查询某个字段是否有值 返回bool类型,true 或 false SELECT ColumnCode,CONVERT(BIT,CASE WHEN LEN(ColumnCode) > 0 THEN 1 ELSE 0 END) AS HasValue FROM dbo.TF_LessonCatalog...

紫光展锐5G芯T820 解锁全新应用场景,让机器人更智能
数字经济的持续发展正推动机器人产业成为风口赛道。工信部数据显示,2023年上半年,我国工业机器人产量达22.2万套,同比增长5.4%;服务机器人产量为353万套,同比增长9.6%。 作为国内商用服务机器人领先企业,云…...

秋招前端面试题总结
1、this指向问题,以前总是迷糊,现在总算是一知半解了。应当遵循以下原则,应该就能做对题目了。 如果一个标准函数,也就是非箭头函数,作为某个对象的方法被调用时,那么这个this指向的就是这个对象。涉及到闭…...

【入门篇】ClickHouse 数据类型
文章目录 1. 引言2. ClickHouse 数据类型2.1 基本数据类型2.1.1 整型2.1.2 浮点型2.1.3 字符串型 2.2 复合数据类型2.2.1 数组2.2.2 枚举类型2.2.3 元组2.2.4 Map2.2.5 Nullable 2.3 特殊数据类型2.3.1 日期和时间类型2.3.2 UUID2.3.3 IP 地址2.3.4 AggregateFunction 2.4 数据…...

关于Python数据分析,这里有一条高效的学习路径
无处不在的数据分析 谷歌的数据分析可以预测一个地区即将爆发的流感,从而进行针对性的预防;淘宝可以根据你浏览和消费的数据进行分析,为你精准推荐商品;口碑极好的网易云音乐,通过其相似性算法,为不同的人…...

基于 json-server 工具,模拟实现后端接口服务环境
文章目录 本地配置后端接口一、安装json-server1、安装 JSON 服务器 安装 JSON 服务器2、创建一个db.json包含一些数据的文件(重点)3、启动 JSON 服务器 启动 JSON 服务器4、现在如果你访问http://localhost:3000/posts/1,你会得到 本地配置后…...

想要精通算法和SQL的成长之路 - 课程表II
想要精通算法和SQL的成长之路 - 课程表 前言一. 课程表II (拓扑排序)1.1 拓扑排序1.2 题解 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 课程表II (拓扑排序) 原题链接 1.1 拓扑排序 核心知识: 拓扑排序是专…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
