【项目经验】：elementui多选表格默认选中
一.需求
在页面刚打开就默认选中指定项。
二.方法Table Methods
| toggleRowSelection | 用于多选表格，切换某一行的选中状态，如果使用了第二个参数，则是设置这一行选中与否（selected 为 true 则选中） | row, selected |
详细请看elementui官网https://element.eleme.io/#/zh-CN/component/table
三.代码
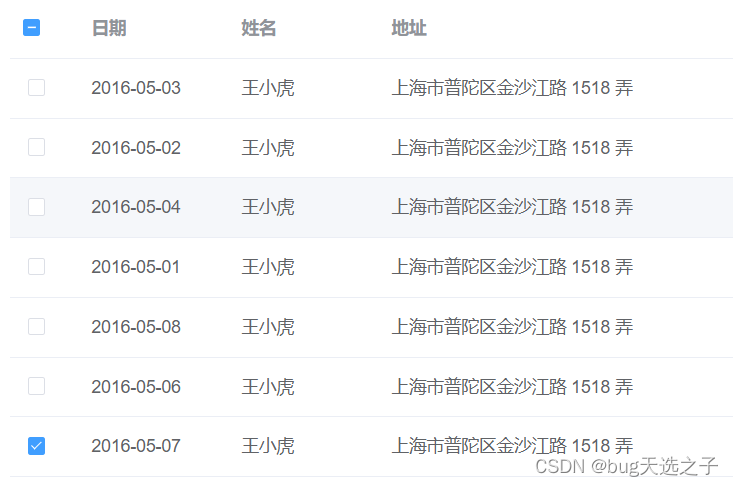
mounted () {// multipleSelection 想选中的数据 tableData表格数据this.$nextTick(() => {this.multipleSelection.forEach(row => {this.$refs.multipleTable.toggleRowSelection(this.tableData.find(item => {return row.date == item.date;}), true)})})},四.效果图
相关文章：
【项目经验】：elementui多选表格默认选中
一.需求 在页面刚打开就默认选中指定项。 二.方法Table Methods toggleRowSelection用于多选表格，切换某一行的选中状态，如果使用了第二个参数，则是设置这一行选中与否（selected 为 true 则选中）row, selected 详细…...
外星人入侵游戏-(创新版)
🌈write in front🌈 🧸大家好，我是Aileen🧸.希望你看完之后，能对你有所帮助，不足请指正！共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
HTML 学习笔记（基础）
它是超文本标记语言，由一大堆约定俗成的标签组成，而其标签里一般又有一些属性值可以设置。 W3C标准：网页主要三大部分 结构：HTML表现：CSS行为：JavaScript <!DOCTYPE html> <html lang"zh-…...
最小二乘法
Least Square Method 1、相关的矩阵公式2、线性回归3、最小二乘法3.1、损失函数（Loss Function）3.2、多维空间的损失函数3.3、解析法求解3.4、梯度下降法求解 1、相关的矩阵公式 P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ…...
使用stelnet进行安全的远程管理
1. telnet有哪些不足？ 2.ssh如何保证数据传输安全？ 需求：远程telnet管理设备 用户定义需要在AAA模式下： 开启远程登录的服务：定义vty接口 然后从R2登录：是可以登录的 同理R3登录： 在R1也可以查…...
python 二手车数据分析以及价格预测
二手车交易信息爬取、数据分析以及交易价格预测 引言一、数据爬取1.1 解析数据1.2 编写代码爬1.2.1 获取详细信息1.2.2 数据处理 二、数据分析2.1 统计分析2.2 可视化分析 三、价格预测3.1 价格趋势分析(特征分析)3.2 价格预测 引言 本文着眼于车辆信息，结合当下较…...
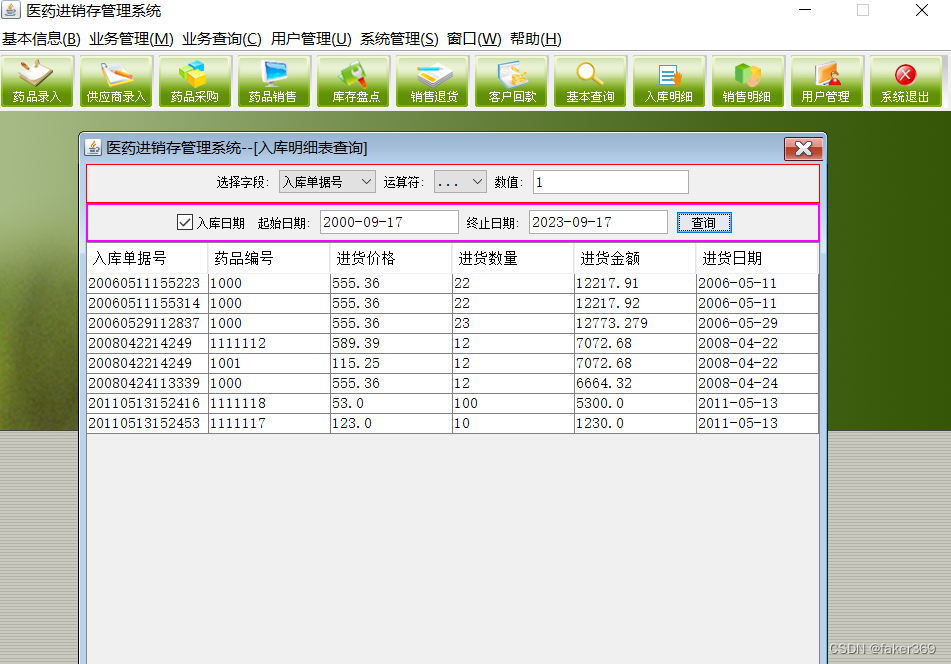
JAVA医药进销存管理系统（附源码+调试）
JAVA医药进销存管理系统 功能描述 （1）登录模块：登录信息等存储在数据库中 （2）基本信息模块：分为药品信息模块、客户情况模块、供应商情况模块； （3）业务管理模块&#x…...
H5 ＜blockquote＞ 标签
主要应用于：内容引用 标签定义及使用说明 <blockquote> 标签定义摘自另一个源的块引用。 浏览器通常会对 <blockquote> 元素进行缩进。 提示和注释 提示：如果标记是不需要段落分隔的短引用，请使用 <q>。 HTML 4.01 与 H…...
nginx配置指南
nginx.conf配置 找到Nginx的安装目录下的nginx.conf文件，该文件负责Nginx的基础功能配置。 配置文件概述 Nginx的主配置文件(conf/nginx.conf)按以下结构组织： 配置块功能描述全局块与Nginx运行相关的全局设置events块与网络连接有关的设置http块代理…...
【数据结构】优先级队列(堆)
文章目录 💐1. 优先级队列1.1 概念 💐2.堆的概念及存储方式2.1 什么是堆2.2 为什么要用完全二叉树描述堆呢？2.3 为什么说堆是在完全二叉树的基础上进行的调整？2.4 使用数组还原完全二叉树 💐3. 堆的常用操作-模拟实现3…...
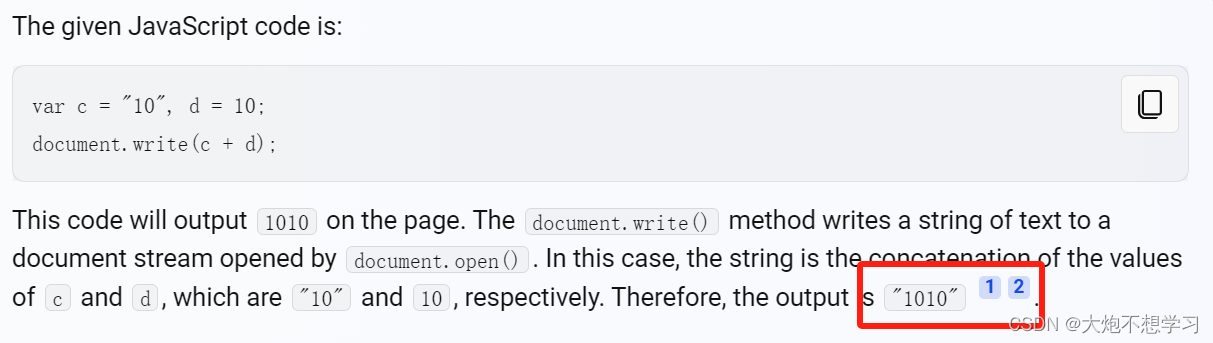
前端笔试2
1.下面哪一个是检验对象是否有一个以自身定义的属性? foo.hasOwnProperty("bar")bar in foo foo["bar"] ! undefinedfoo.bar ! null 解析： bar in foo 检查 foo 对象是否包含名为 bar 的属性，但是这个属性可以是从原型链继承来的&a…...
LeetCode:66.加一
66.加一 来源：力扣（LeetCode） 链接: https://leetcode.cn/problems/plus-one/description/ 给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。 最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外，这个整数…...
Redis 常用命令
目录 全局命令 1）keys 2）exists 3) del(delete) 4）expire 5）type SET命令 GET命令 MSET 和 MGET命令 其他SET命令 计数命令 redis-cli，进入redis 最核心的命令：我们这里只是先介绍 set 和 get 最简单的操作…...
用于字符和字符串的区别)
Integer.valueOf()用于字符和字符串的区别
LeetCode 17 电话号码的字母组合 先贴代码 class Solution {List<String> result new ArrayList<>();String temp new String("");Integer num;public List<String> letterCombinations(String digits) {dfs(digits, 0);return result;} publi…...
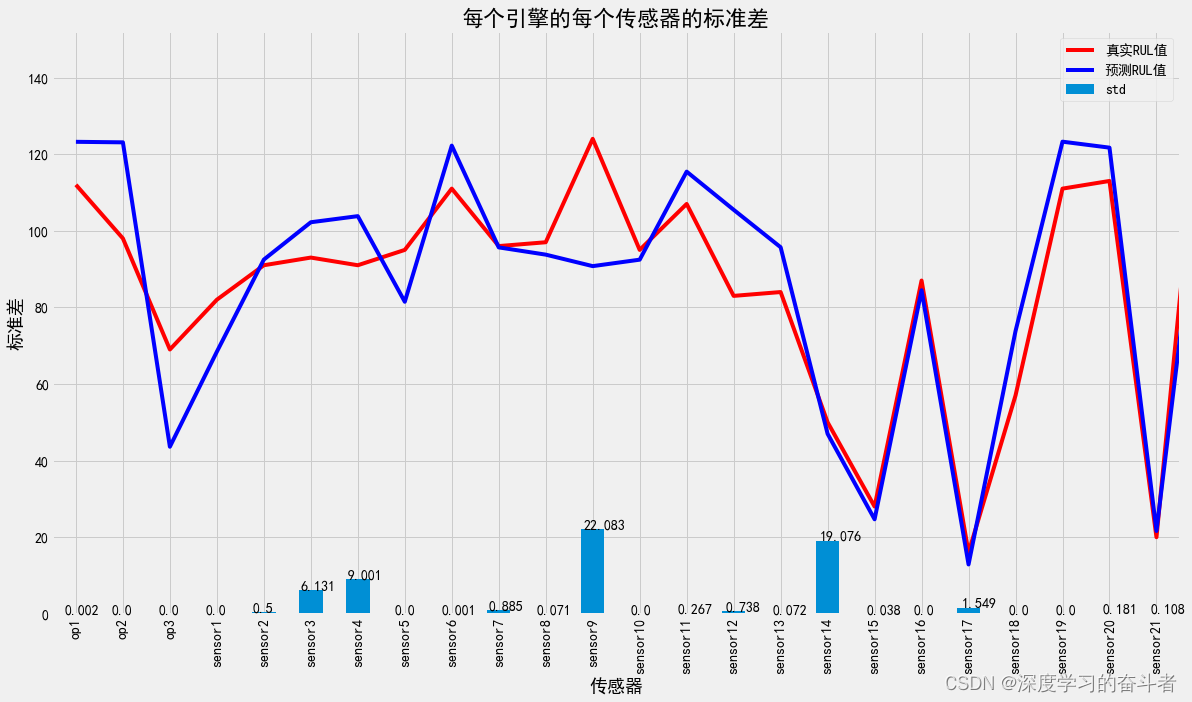
机械寿命预测（基于NASA C-MAPSS数据的剩余使用寿命RUL预测，Python代码，CNN_LSTM模型，有详细中文注释）
1.效果视频：机械寿命预测（NASA涡轮风扇发动机剩余使用寿命RUL预测，Python代码，CNN_LSTM模型，有详细中文注释）_哔哩哔哩_bilibili 环境库版本： 2.数据来源：https://www.nasa.gov/int…...
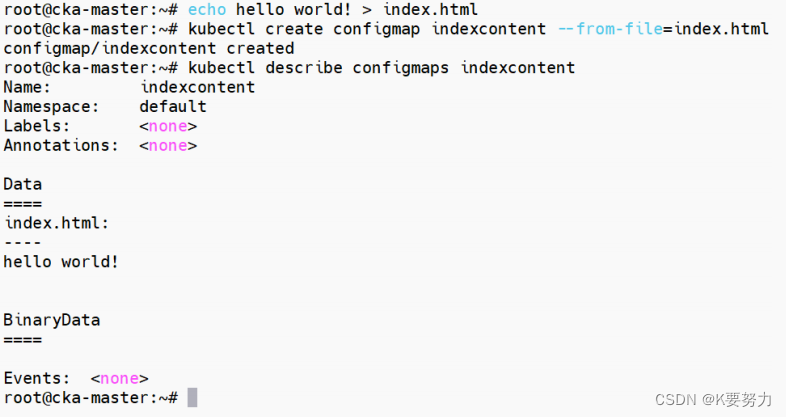
ConfigMaps-1
文章目录 主要内容一.使用 YAML 文件创建1.在data节点创建了一些键值：代码如下（示例）: 2.解释 二.使用命令行创建1.创建了一个名为 person 的键值：代码如下（示例）: 2.解释3.创建了一个 index.html 文件&…...
docker上安装es
安装docker 1 安装docker依赖 yum install -y yum-utils2 设置docker仓库镜像地址 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo3 安装制定版本的docker yum -y install docker-ce-20.10.17-3.el74 查看是否安装成功 y…...
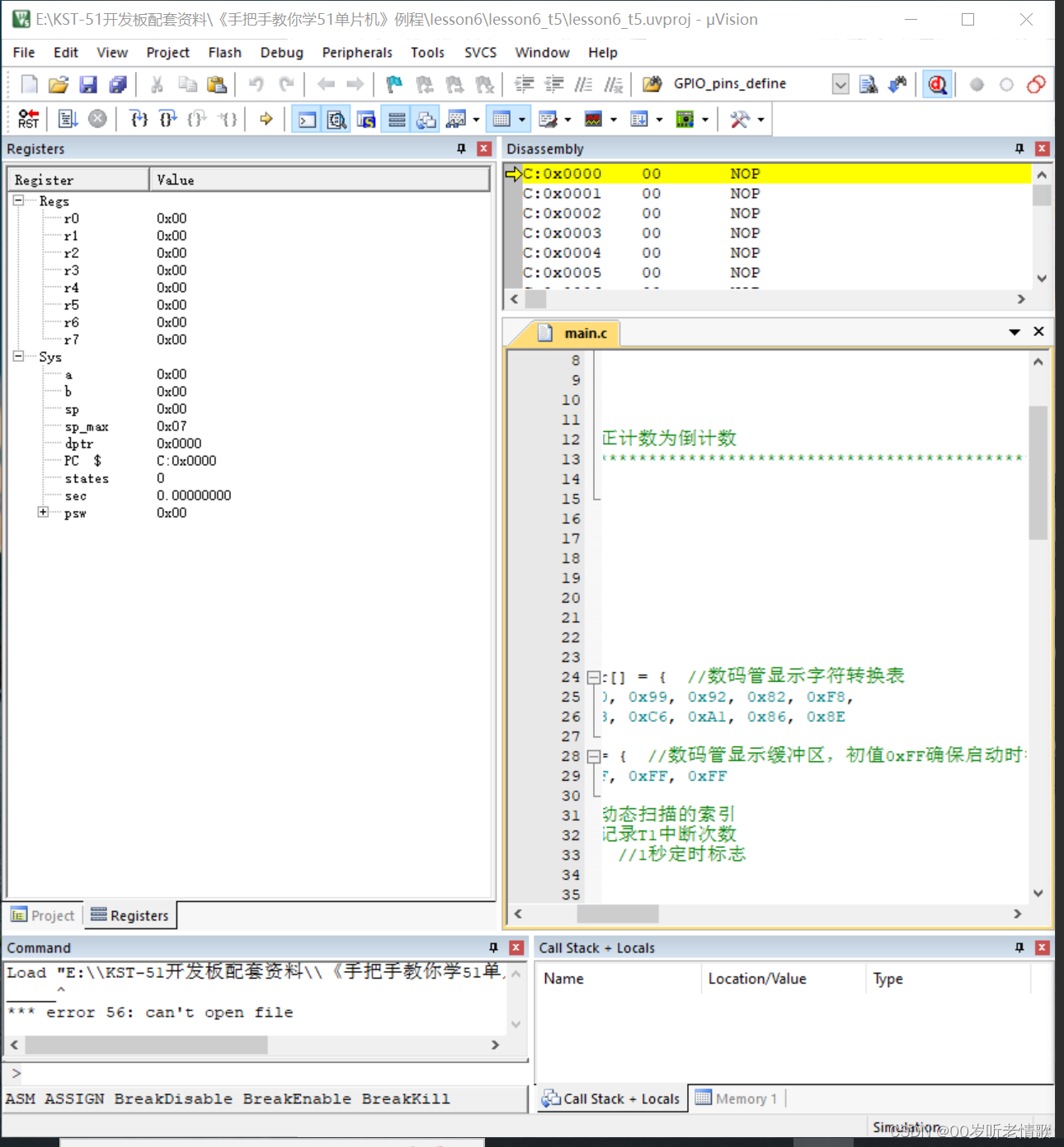
#循循渐进学51单片机#c语言基础和流水灯实现#not.3
1、熟练掌握二进制、十进制和十六进制的转换方法。 多少进制就是多少之间相加，比如十六进制就是十六一次一加；二进制转化十六进制，分成四个一组。 2、C语言变量类型与取值范围，for、while等基本语句的用法。 for、while等基本语句…...
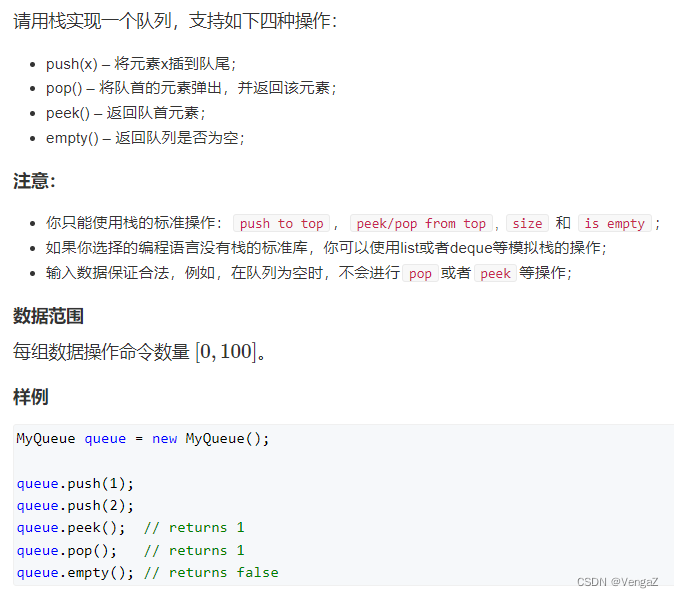
算法刷题 week3
这里写目录标题 1.重建二叉树题目题解(递归) O(n) 2.二叉树的下一个节点题目题解(模拟) O(h) 3.用两个栈实现队列题目题解(栈，队列) O(n) 1.重建二叉树 题目 题解 (递归) O(n) 递归建立整棵二叉树：先递归创建左右子树，然后创建根节点&…...
TCP详解之流量控制
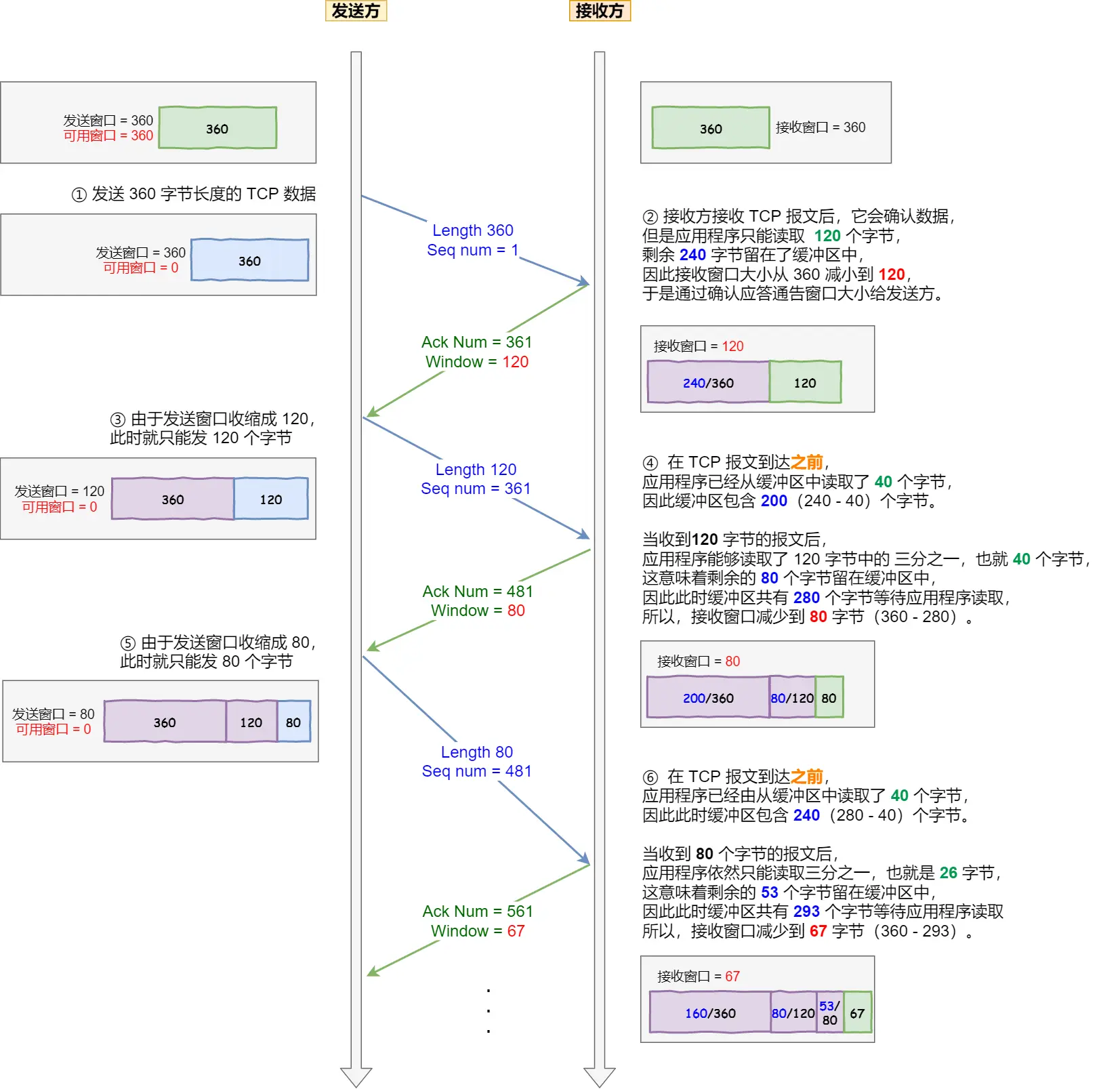
TCP详解之流量控制 发送方不能无脑的发数据给接收方，要考虑接收方处理能力。 如果一直无脑的发数据给对方，但对方处理不过来，那么就会导致触发重发机制，从而导致网络流量的无端的浪费。 为了解决这种现象发生，TCP 提…...
基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook，用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途，下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）
【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...
MySQL 8.0 OCP 英文题库解析（十三）
Oracle 为庆祝 MySQL 30 周年，截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始，将英文题库免费公布出来，并进行解析，帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控，故障处理工具
第2章 虚拟机性能监控，故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令：jps [options] [hostid] 功能：本地虚拟机进程显示进程ID（与ps相同），可同时显示主类&#x…...
3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象，只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意：它移动的位置必须是相连的有内容的单元格…...
【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法，且在 O…...
Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源：全方位解析 Vue 模板（<template> 部分）中的表达式、指令绑定（如 v-bind, v-on）和插值（{{ }}）都在一个特定的作用域内求值。这个作用域由当前 组件…...
多模态学习路线（2）——DL基础系列
目录 前言 一、归一化 1. Layer Normalization (LN) 2. Batch Normalization (BN) 3. Instance Normalization (IN) 4. Group Normalization (GN) 5. Root Mean Square Normalization（RMSNorm） 二、激活函数 1. Sigmoid激活函数（二分类&…...