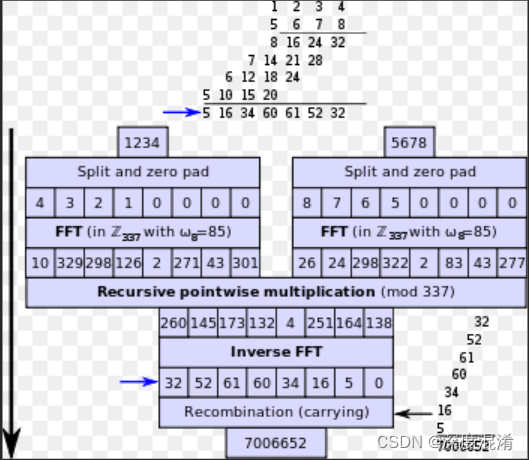
C#,《小白学程序》第二十六课:大数乘法(BigInteger Multiply)的Toom-Cook 3算法及源程序
凑数的,仅供参考。
1 文本格式
/// <summary>
/// 《小白学程序》第二十六课:大数(BigInteger)的Toom-Cook 3乘法
/// Toom-Cook 3-Way Multiplication
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static string toom_cook3_multiply(string a, string b)
{
int n = Math.Max(a.Length, b.Length);
int[] ra = string_to_digitals(a, n);
int[] rb = string_to_digitals(b, n);
toom_cook3_process_00(ra, rb, out int[] rz);
toom_cook3_carry(rz, n * 2);
return digitals_to_string(rz);
}
/// <summary>
/// 短数字的乘法(常规乘法,小学生算法)
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_normal(int[] a, int[] b, ref int[] z)
{
int n = a.Length;
for (int j = 0; j < n; j++)
{
for (int i = 0; i < n; i++)
{
z[j + i] += a[i] * b[j];
}
}
}
/// <summary>
/// 完全按原始C++代码改写;运行成功;
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_process_01(int[] a, int[] b, out int[] z)
{
int n = a.Length;
int n1 = n * 1 / 3;
int n2 = n * 2 / 3;
int n3 = n * 3 / 3;
int n4 = n * 4 / 3;
z = new int[n * 2];
if (n <= 9)
{
toom_cook3_normal(a, b, ref z);
return;
}
// int *a0 = &a[0];
// Multiplicand / right side array pointer
int a0 = 0;
// int *a1 = &a[tLen / 3];
// Multiplicand / central array pointer
int a1 = n1;
// int *a2 = &a[tLen * 2/ 3];
// Multiplicand / left side array pointer
int a2 = n2;// n * 2 / 3;
// int *b0 = &b[0];
// Multiplier / right side array pointer
int b0 = 0;
// int *b1 = &b[tLen / 3];
// Multiplier / central array pointer
int b1 = n1;
// int *b2 = &b[tLen * 2 / 3];
// Multiplier / left side array pointer
int b2 = n2;// n * 2 / 3;
// int *c0 = &z[(tLen / 3) * 0];
int[] c0 = new int[n2];
int[] c1 = new int[n2];
// int *c2 = &z[(tLen / 3) * 2];
int[] c2 = new int[n2];
int[] c3 = new int[n2];
// int *c4 = &z[(tLen / 3) * 4];
int[] c4 = new int[n2];
int[] a_m2 = new int[n1]; // a(-2)
int[] a_m1 = new int[n1]; // a(-1)
int[] a_0 = new int[n1]; // a(0)
int[] a_1 = new int[n1]; // a(1)
int[] a_inf = new int[n1]; // a(inf)
int[] b_m2 = new int[n1]; // b-2)
int[] b_m1 = new int[n1]; // b-1)
int[] b_0 = new int[n1]; // b(0)
int[] b_1 = new int[n1]; // b(1)
int[] b_inf = new int[n1]; // b(inf)
// ==== a(-2) = 4 * a2 - 2 * a1 + a0, b(-2) = 4 * b2 - 2 * b1 + b0
for (int i = 0; i < n1; i++)
{
a_m2[i] = (a[a2 + i] << 2) - (a[a1 + i] << 1) + a[a0 + i];
b_m2[i] = (b[b2 + i] << 2) - (b[b1 + i] << 1) + b[b0 + i];
}
// ==== c(-2) = a(-2) * b(-2)
toom_cook3_process_01(a_m2, b_m2, out int[] c_m2);
// ==== a(-1) = a2 - a1 + a0, b(-1) = b2 - b1 + b0
for (int i = 0; i < n1; i++)
{
a_m1[i] = a[a2 + i] - a[a1 + i] + a[a0 + i];
b_m1[i] = b[b2 + i] - b[b1 + i] + b[b0 + i];
}
// ==== c(-1) = a(-1) * b(-1)
toom_cook3_process_01(a_m1, b_m1, out int[] c_m1);
// ==== a(0) = a0, b(0) = b0
for (int i = 0; i < n1; i++)
{
a_0[i] = a[a0 + i];
b_0[i] = b[b0 + i];
}
// ==== c(0) = a(0) * b(0)
toom_cook3_process_01(a_0, b_0, out int[] c_0);
// ==== a(1) = a2 + a1 + a0, b(1) = b2 + b1 + b0
for (int i = 0; i < n1; i++)
{
a_1[i] = a[a2 + i] + a[a1 + i] + a[a0 + i];
b_1[i] = b[b2 + i] + b[b1 + i] + b[b0 + i];
}
// ==== c(1) = a(1) * b(1)
toom_cook3_process_01(a_1, b_1, out int[] c_1);
// ==== a(inf) = a2, b(inf) = b2
for (int i = 0; i < n1; i++)
{
a_inf[i] = a[a2 + i];
b_inf[i] = b[b2 + i];
}
// ==== c(inf) = a(inf) * b(inf)
toom_cook3_process_01(a_inf, b_inf, out int[] c_inf);
// ==== c4 = 6 * c(inf) / 6
for (int i = 0; i < n2; i++)
{
c4[i] = c_inf[i];
}
// ==== c3 = -c(-2) + 3 * c(-1) - 3 * c(0) + c(1) + 12 * c(inf) / 6
for (int i = 0; i < n2; i++)
{
c3[i] = -c_m2[i];
c3[i] += (c_m1[i] << 1) + c_m1[i];
c3[i] -= (c_0[i] << 1) + c_0[i];
c3[i] += c_1[i];
c3[i] += (c_inf[i] << 3) + (c_inf[i] << 2);
c3[i] /= 6;
}
// ==== c2 = 3 * c(-1) - 6 * c(0) + 3 * c(1) - 6 * c(inf) / 6
for (int i = 0; i < n2; i++)
{
c2[i] = (c_m1[i] << 1) + c_m1[i];
c2[i] -= (c_0[i] << 2) + (c_0[i] << 1);
c2[i] += (c_1[i] << 1) + c_1[i];
c2[i] -= (c_inf[i] << 2) + (c_inf[i] << 1);
c2[i] /= 6;
}
// ==== c1 = c(-2) - 6 * c(-1) + 3 * c(0) + 2 * c(1) - 12 * c(inf) / 6
for (int i = 0; i < n2; i++)
{
c1[i] = c_m2[i];
c1[i] -= (c_m1[i] << 2) + (c_m1[i] << 1);
c1[i] += (c_0[i] << 1) + c_0[i];
c1[i] += (c_1[i] << 1);
c1[i] -= (c_inf[i] << 3) + (c_inf[i] << 2);
c1[i] /= 6;
}
// ==== c0 = 6 * c(0) / 6
for (int i = 0; i < n2; i++)
{
c0[i] = c_0[i];
}
// ==== z = c4 * x^4 + c3 * x^3 + c2 * x^2 + c1 * x + c0
for (int i = 0; i < n2; i++)
{
z[i + n4] += c4[i];
z[i + n3] += c3[i];
z[i + n2] += c2[i];
z[i + n1] += c1[i];
z[i] += c0[i];
}
}
/// <summary>
/// 乘积和的进位计算
/// </summary>
/// <param name="a"></param>
/// <param name="n"></param>
/// <exception cref="Exception"></exception>
private static void toom_cook3_carry(int[] a, int n)
{
int cr = 0;
for (int i = 0; i < n; i++)
{
a[i] += cr;
if (a[i] < 0)
{
cr = -(-(a[i] + 1) / 10 + 1);
}
else
{
cr = a[i] / 10;
}
a[i] -= cr * 10;
}
if (cr != 0)
{
// Overflow
throw new Exception("OVERFLOW! cr=" + cr);
}
}
2 代码格式
/// <summary>
/// 《小白学程序》第二十六课:大数(BigInteger)的Toom-Cook 3乘法
/// Toom-Cook 3-Way Multiplication
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static string toom_cook3_multiply(string a, string b)
{int n = Math.Max(a.Length, b.Length);int[] ra = string_to_digitals(a, n);int[] rb = string_to_digitals(b, n);toom_cook3_process_00(ra, rb, out int[] rz);toom_cook3_carry(rz, n * 2);return digitals_to_string(rz);
}/// <summary>
/// 短数字的乘法(常规乘法,小学生算法)
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_normal(int[] a, int[] b, ref int[] z)
{int n = a.Length;for (int j = 0; j < n; j++){for (int i = 0; i < n; i++){z[j + i] += a[i] * b[j];}}
}/// <summary>
/// 完全按原始C++代码改写;运行成功;
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="z"></param>
private static void toom_cook3_process_01(int[] a, int[] b, out int[] z)
{int n = a.Length;int n1 = n * 1 / 3;int n2 = n * 2 / 3;int n3 = n * 3 / 3;int n4 = n * 4 / 3;z = new int[n * 2];if (n <= 9){toom_cook3_normal(a, b, ref z);return;}// int *a0 = &a[0];// Multiplicand / right side array pointerint a0 = 0;// int *a1 = &a[tLen / 3];// Multiplicand / central array pointerint a1 = n1;// int *a2 = &a[tLen * 2/ 3];// Multiplicand / left side array pointerint a2 = n2;// n * 2 / 3;// int *b0 = &b[0];// Multiplier / right side array pointerint b0 = 0;// int *b1 = &b[tLen / 3];// Multiplier / central array pointerint b1 = n1;// int *b2 = &b[tLen * 2 / 3];// Multiplier / left side array pointerint b2 = n2;// n * 2 / 3;// int *c0 = &z[(tLen / 3) * 0];int[] c0 = new int[n2];int[] c1 = new int[n2];// int *c2 = &z[(tLen / 3) * 2];int[] c2 = new int[n2];int[] c3 = new int[n2];// int *c4 = &z[(tLen / 3) * 4];int[] c4 = new int[n2];int[] a_m2 = new int[n1]; // a(-2)int[] a_m1 = new int[n1]; // a(-1)int[] a_0 = new int[n1]; // a(0)int[] a_1 = new int[n1]; // a(1)int[] a_inf = new int[n1]; // a(inf)int[] b_m2 = new int[n1]; // b-2)int[] b_m1 = new int[n1]; // b-1)int[] b_0 = new int[n1]; // b(0)int[] b_1 = new int[n1]; // b(1)int[] b_inf = new int[n1]; // b(inf)// ==== a(-2) = 4 * a2 - 2 * a1 + a0, b(-2) = 4 * b2 - 2 * b1 + b0for (int i = 0; i < n1; i++){a_m2[i] = (a[a2 + i] << 2) - (a[a1 + i] << 1) + a[a0 + i];b_m2[i] = (b[b2 + i] << 2) - (b[b1 + i] << 1) + b[b0 + i];}// ==== c(-2) = a(-2) * b(-2)toom_cook3_process_01(a_m2, b_m2, out int[] c_m2);// ==== a(-1) = a2 - a1 + a0, b(-1) = b2 - b1 + b0for (int i = 0; i < n1; i++){a_m1[i] = a[a2 + i] - a[a1 + i] + a[a0 + i];b_m1[i] = b[b2 + i] - b[b1 + i] + b[b0 + i];}// ==== c(-1) = a(-1) * b(-1)toom_cook3_process_01(a_m1, b_m1, out int[] c_m1);// ==== a(0) = a0, b(0) = b0for (int i = 0; i < n1; i++){a_0[i] = a[a0 + i];b_0[i] = b[b0 + i];}// ==== c(0) = a(0) * b(0)toom_cook3_process_01(a_0, b_0, out int[] c_0);// ==== a(1) = a2 + a1 + a0, b(1) = b2 + b1 + b0for (int i = 0; i < n1; i++){a_1[i] = a[a2 + i] + a[a1 + i] + a[a0 + i];b_1[i] = b[b2 + i] + b[b1 + i] + b[b0 + i];}// ==== c(1) = a(1) * b(1)toom_cook3_process_01(a_1, b_1, out int[] c_1);// ==== a(inf) = a2, b(inf) = b2for (int i = 0; i < n1; i++){a_inf[i] = a[a2 + i];b_inf[i] = b[b2 + i];}// ==== c(inf) = a(inf) * b(inf)toom_cook3_process_01(a_inf, b_inf, out int[] c_inf);// ==== c4 = 6 * c(inf) / 6for (int i = 0; i < n2; i++){c4[i] = c_inf[i];}// ==== c3 = -c(-2) + 3 * c(-1) - 3 * c(0) + c(1) + 12 * c(inf) / 6for (int i = 0; i < n2; i++){c3[i] = -c_m2[i];c3[i] += (c_m1[i] << 1) + c_m1[i];c3[i] -= (c_0[i] << 1) + c_0[i];c3[i] += c_1[i];c3[i] += (c_inf[i] << 3) + (c_inf[i] << 2);c3[i] /= 6;}// ==== c2 = 3 * c(-1) - 6 * c(0) + 3 * c(1) - 6 * c(inf) / 6for (int i = 0; i < n2; i++){c2[i] = (c_m1[i] << 1) + c_m1[i];c2[i] -= (c_0[i] << 2) + (c_0[i] << 1);c2[i] += (c_1[i] << 1) + c_1[i];c2[i] -= (c_inf[i] << 2) + (c_inf[i] << 1);c2[i] /= 6;}// ==== c1 = c(-2) - 6 * c(-1) + 3 * c(0) + 2 * c(1) - 12 * c(inf) / 6for (int i = 0; i < n2; i++){c1[i] = c_m2[i];c1[i] -= (c_m1[i] << 2) + (c_m1[i] << 1);c1[i] += (c_0[i] << 1) + c_0[i];c1[i] += (c_1[i] << 1);c1[i] -= (c_inf[i] << 3) + (c_inf[i] << 2);c1[i] /= 6;}// ==== c0 = 6 * c(0) / 6for (int i = 0; i < n2; i++){c0[i] = c_0[i];}// ==== z = c4 * x^4 + c3 * x^3 + c2 * x^2 + c1 * x + c0for (int i = 0; i < n2; i++){z[i + n4] += c4[i];z[i + n3] += c3[i];z[i + n2] += c2[i];z[i + n1] += c1[i];z[i] += c0[i];}
}/// <summary>/// 乘积和的进位计算/// </summary>/// <param name="a"></param>/// <param name="n"></param>/// <exception cref="Exception"></exception>private static void toom_cook3_carry(int[] a, int n){int cr = 0;for (int i = 0; i < n; i++){a[i] += cr;if (a[i] < 0){cr = -(-(a[i] + 1) / 10 + 1);}else{cr = a[i] / 10;}a[i] -= cr * 10;}if (cr != 0){// Overflowthrow new Exception("OVERFLOW! cr=" + cr);}}相关文章:

C#,《小白学程序》第二十六课:大数乘法(BigInteger Multiply)的Toom-Cook 3算法及源程序
凑数的,仅供参考。 1 文本格式 /// <summary> /// 《小白学程序》第二十六课:大数(BigInteger)的Toom-Cook 3乘法 /// Toom-Cook 3-Way Multiplication /// </summary> /// <param name"a"></par…...
destoon自定义一个archiver内容文档
在archiver目录建立以下代码: <?php define(DT_REWRITE, true); require ../common.inc.php; $EXT[archiver_enable] or dheader(DT_PATH); //$DT_BOT or dheader(DT_PATH); $N $M $T array(); $mid or $mid 5; $vmid $list 0; foreach($MODULE as $k>…...
5-1 Dataset和DataLoader
Pytorch通常使用Dataset和DataLoader这两个工具类来构建数据管道。 Dataset定义了数据集的内容,它相当于一个类似列表的数据结构,具有确定的长度,能够用索引获取数据集中的元素。 而DataLoader定义了按batch加载数据集的方法,它是…...
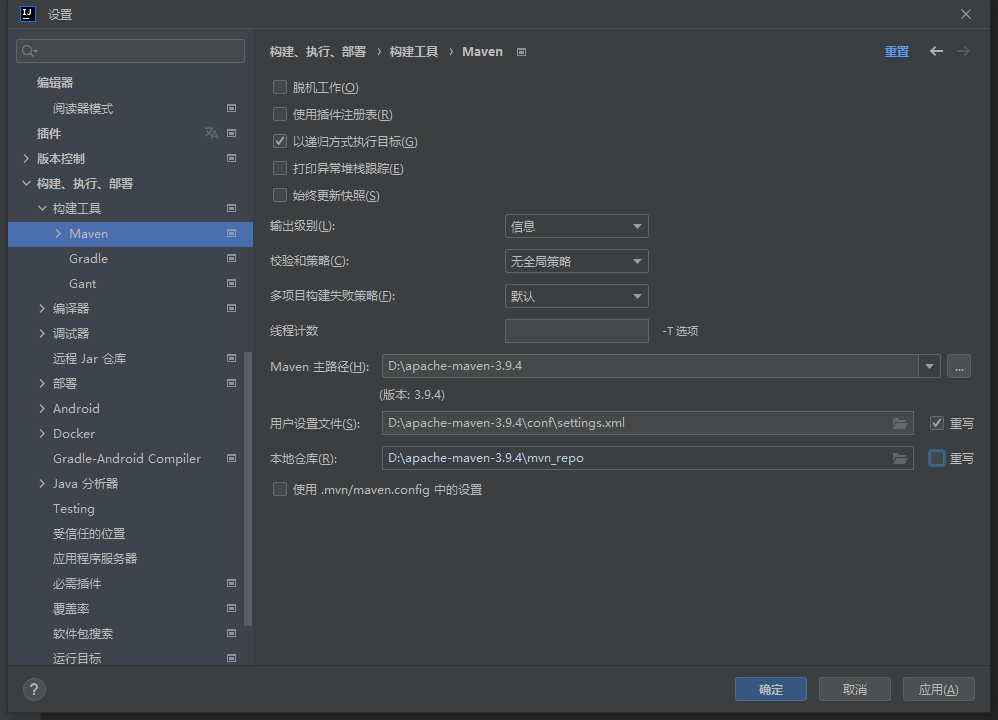
IDEA创建完Maven工程后,右下角一直显示正在下载Maven插件
原因: 这是由于新建的Maven工程,IDEA会用它内置的默认的Maven版本,使用国外的网站下载Maven所需的插件,速度很慢 。 解决方式: 每次创建 Project 后都需要设置 Maven 家目录位置(就是我们自己下载的Mav…...

最新清理删除Mac电脑内存空间方法教程
Mac电脑使用的时间越久,系统的运行就会变的越卡顿,这是Mac os会出现的正常现象,卡顿的原因主要是系统缓存文件占用了较多的磁盘空间,或者Mac的内存空间已满。如果你的Mac运行速度变慢,很有可能是因为磁盘内存被过度占用…...

【调试经验】MySQL - fatal error: mysql/mysql.h: 没有那个文件或目录
机器环境: Ubuntu 22.04.3 LTS 报错问题 在编译一个项目时出现了一段SQL报错: CGImysql/sql_connection_pool.cpp:1:10: fatal error: mysql/mysql.h: 没有那个文件或目录 1 | #include <mysql/mysql.h> | ^~~~~~~~~~~~~~~ c…...

腾讯mini项目-【指标监控服务重构】2023-08-12
今日已办 Watermill Handler 将 4 个阶段的逻辑处理定义为 Handler 测试发现,添加的 handler 会被覆盖掉,故考虑添加为 middleware 且 4 个阶段的处理逻辑针对不同 topic 是相同的。 参考https://watermill.io/docs/messages-router/实现不同topic&am…...

kubeadm部署k8sv1.24使用cri-docker做为CRI
目的 测试使用cri-docker做为containerd和docker的中间层垫片。 规划 IP系统主机名10.0.6.5ubuntu 22.04.3 jammymaster01.kktb.org10.0.6.6ubuntu 22.04.3 jammymaster02.kktb.org10.0.6.7ubuntu 22.04.3 jammymaster03.kktb.org 配置 步骤: 系统优化 禁用sw…...
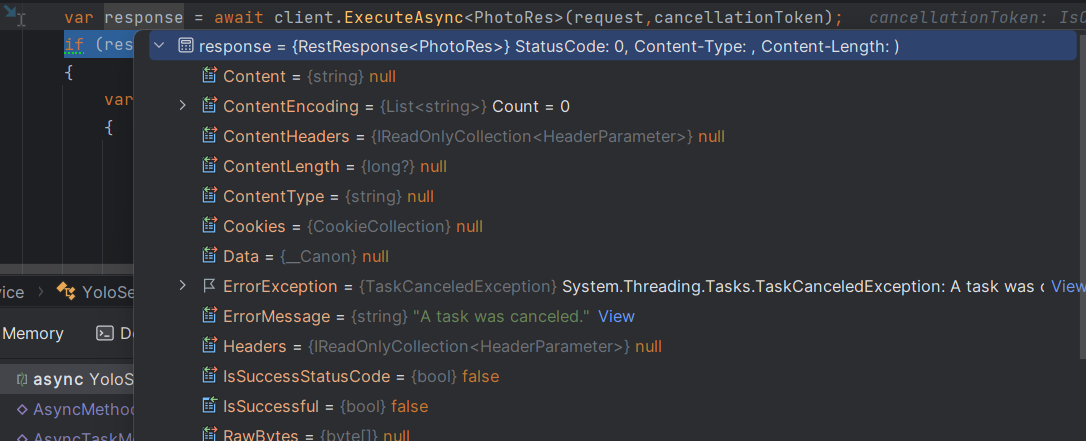
在c#中使用CancellationToken取消任务
目录 🚀介绍: 🐤简单举例 🚀IsCancellationRequested 🚀ThrowIfCancellationRequested 🐤在控制器中使用 🚀通过异步方法的参数使用cancellationToken 🚀api结合ThrowIfCancel…...
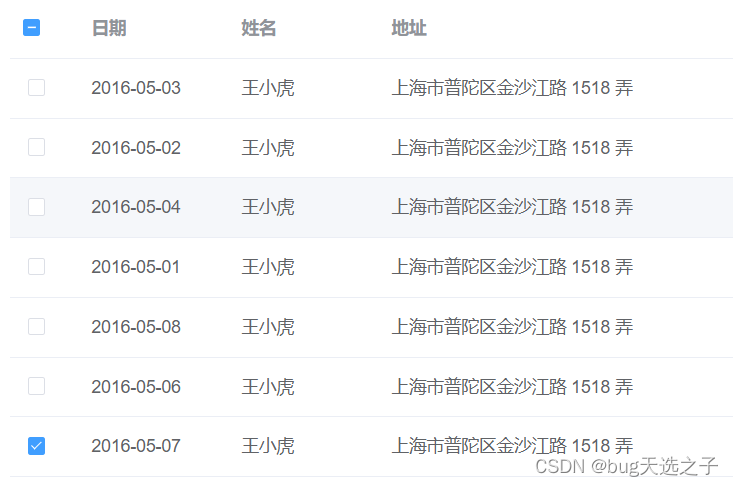
【项目经验】:elementui多选表格默认选中
一.需求 在页面刚打开就默认选中指定项。 二.方法Table Methods toggleRowSelection用于多选表格,切换某一行的选中状态,如果使用了第二个参数,则是设置这一行选中与否(selected 为 true 则选中)row, selected 详细…...

外星人入侵游戏-(创新版)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
HTML 学习笔记(基础)
它是超文本标记语言,由一大堆约定俗成的标签组成,而其标签里一般又有一些属性值可以设置。 W3C标准:网页主要三大部分 结构:HTML表现:CSS行为:JavaScript <!DOCTYPE html> <html lang"zh-…...

最小二乘法
Least Square Method 1、相关的矩阵公式2、线性回归3、最小二乘法3.1、损失函数(Loss Function)3.2、多维空间的损失函数3.3、解析法求解3.4、梯度下降法求解 1、相关的矩阵公式 P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ…...

使用stelnet进行安全的远程管理
1. telnet有哪些不足? 2.ssh如何保证数据传输安全? 需求:远程telnet管理设备 用户定义需要在AAA模式下: 开启远程登录的服务:定义vty接口 然后从R2登录:是可以登录的 同理R3登录: 在R1也可以查…...

python 二手车数据分析以及价格预测
二手车交易信息爬取、数据分析以及交易价格预测 引言一、数据爬取1.1 解析数据1.2 编写代码爬1.2.1 获取详细信息1.2.2 数据处理 二、数据分析2.1 统计分析2.2 可视化分析 三、价格预测3.1 价格趋势分析(特征分析)3.2 价格预测 引言 本文着眼于车辆信息,结合当下较…...
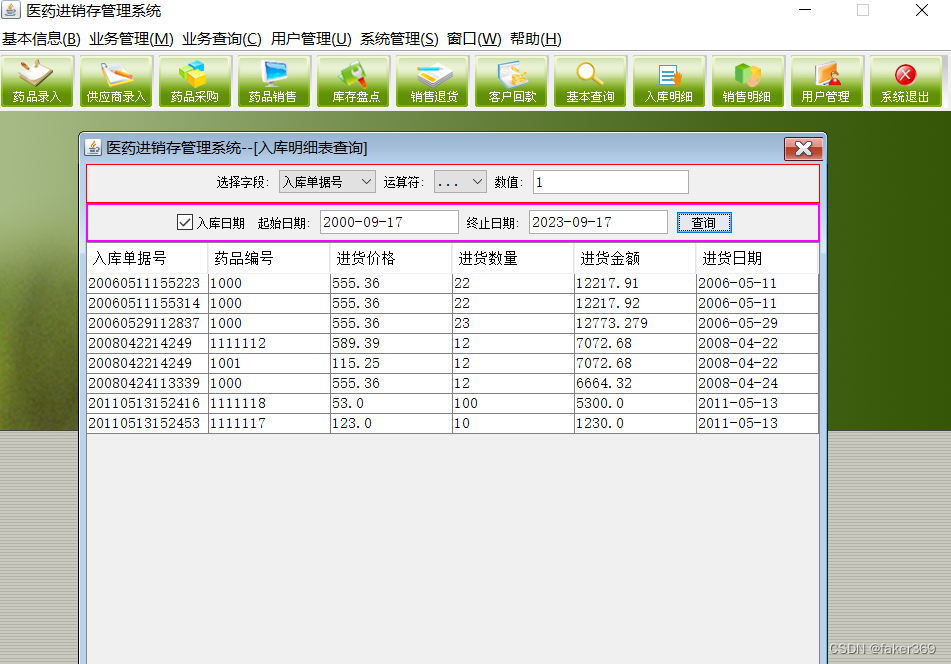
JAVA医药进销存管理系统(附源码+调试)
JAVA医药进销存管理系统 功能描述 (1)登录模块:登录信息等存储在数据库中 (2)基本信息模块:分为药品信息模块、客户情况模块、供应商情况模块; (3)业务管理模块&#x…...

H5 <blockquote> 标签
主要应用于:内容引用 标签定义及使用说明 <blockquote> 标签定义摘自另一个源的块引用。 浏览器通常会对 <blockquote> 元素进行缩进。 提示和注释 提示:如果标记是不需要段落分隔的短引用,请使用 <q>。 HTML 4.01 与 H…...
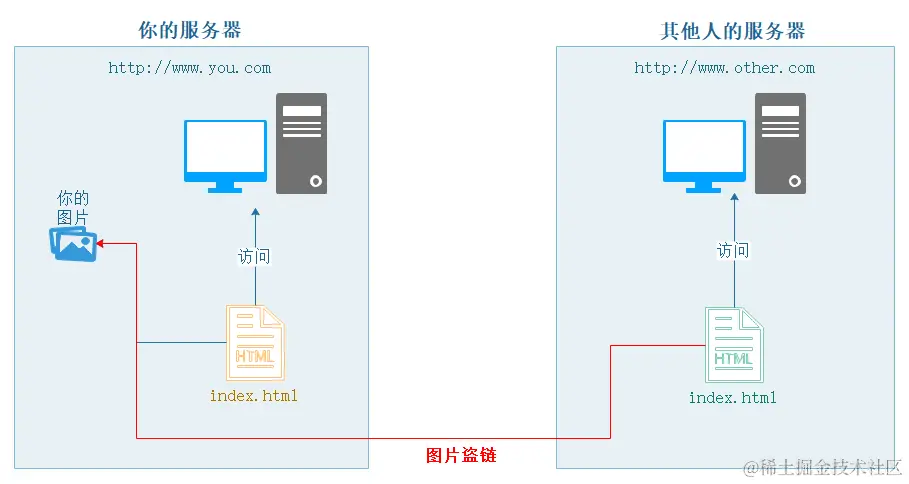
nginx配置指南
nginx.conf配置 找到Nginx的安装目录下的nginx.conf文件,该文件负责Nginx的基础功能配置。 配置文件概述 Nginx的主配置文件(conf/nginx.conf)按以下结构组织: 配置块功能描述全局块与Nginx运行相关的全局设置events块与网络连接有关的设置http块代理…...

【数据结构】优先级队列(堆)
文章目录 💐1. 优先级队列1.1 概念 💐2.堆的概念及存储方式2.1 什么是堆2.2 为什么要用完全二叉树描述堆呢?2.3 为什么说堆是在完全二叉树的基础上进行的调整?2.4 使用数组还原完全二叉树 💐3. 堆的常用操作-模拟实现3…...
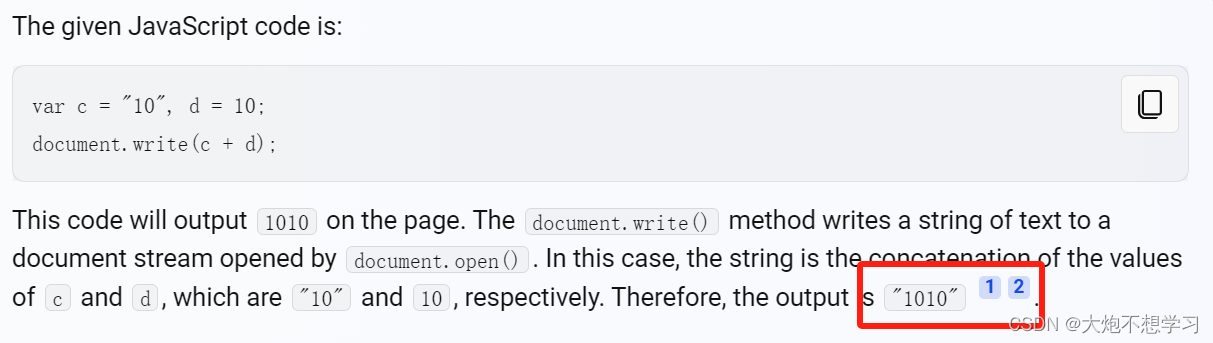
前端笔试2
1.下面哪一个是检验对象是否有一个以自身定义的属性? foo.hasOwnProperty("bar")bar in foo foo["bar"] ! undefinedfoo.bar ! null 解析: bar in foo 检查 foo 对象是否包含名为 bar 的属性,但是这个属性可以是从原型链继承来的&a…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
