代码随想录day38
动态规划五部曲
- 确定dp数组以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509. 斐波那契数
https://leetcode.cn/problems/fibonacci-number/
class Solution {public int fib(int n) {if(n==0) return 0;if(n<3) return 1;int[] dp = new int[n];dp[0]=1;dp[1]=1;for(int i=2;i<n;i++){dp[i]=dp[i-1]+dp[i-2];}return dp[n-1];}
}
讲解的简化版本。
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}
70. 爬楼梯
https://leetcode.cn/problems/climbing-stairs/
和斐波那契差不多。
class Solution {public int climbStairs(int n) {if(n<4) return n;int[] dp=new int[n];int a=2;int b=3;int c=5;for(int i=3;i<n;i++){c=a+b;a=b;b=c;}return c;}
}
746. 使用最小花费爬楼梯
https://leetcode.cn/problems/min-cost-climbing-stairs/
这个感觉最后一步不花费更好理解
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp=new int[cost.length];dp[0]=cost[0];dp[1]=cost[1];for(int i=2;i<cost.length;i++){dp[i]=Math.min(dp[i - 1], dp[i - 2]) + cost[i];}return Math.min(dp[cost.length-1],dp[cost.length-2]);}
}
相关文章:

代码随想录day38
动态规划五部曲 确定dp数组以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 509. 斐波那契数 https://leetcode.cn/problems/fibonacci-number/ class Solution {public int fib(int n) {if(n0) return 0;if(n<3) return 1;int[] dp new int[n]…...
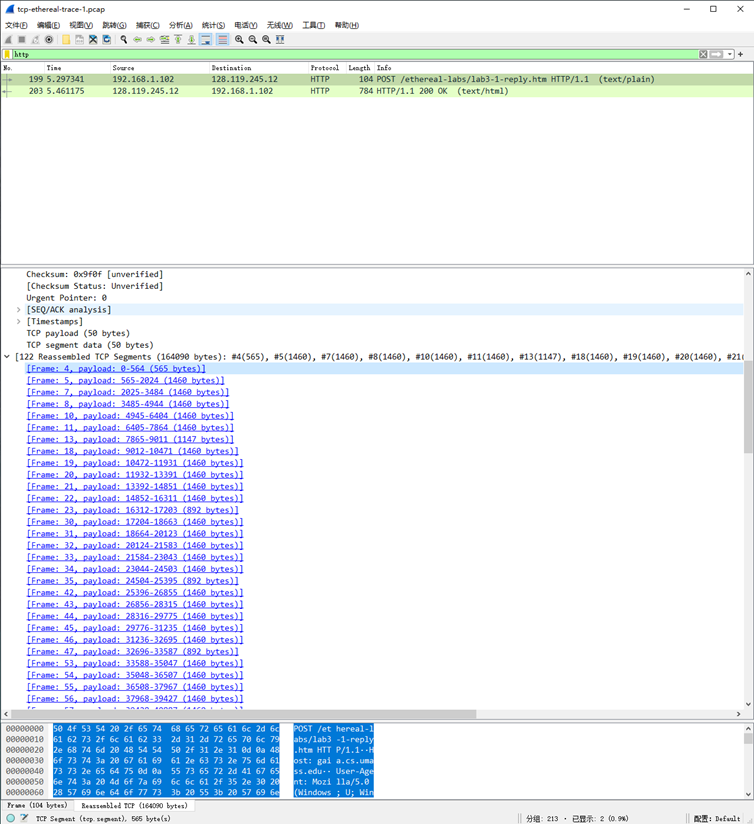
《计算机网络:自顶向下方法》实验5:TCP
Q1 包含HTTP POST消息的TCP报文段的序号是多少?注意:为了发现POST 命令, 你需要在wireshark底部的报文内容域窗口中去查找,查找数据中包含 “POST”的段。 如图所示,由报文中的POST 和 HTTP/1.1可知,其包含HTTP POST消息; TCP报文段的序号可见TCP报文: Sequence Number:…...

【踩坑指南】Stable Diffusion 服务器端部署笔记
文章目录下载github文件配置环境ckpt文件权重下载生成图像NSFW检查(瑟图过滤)下载github文件 https://github.com/CompVis/stable-diffusion 这个网址,下载压缩包解压,也可以用git clone下载 配置环境 这一步坑最多,…...

[qiankun]-多页签缓存
[qiankun]-多页签缓存环境功能需求多页签缓存方案方案1.主服务进行html替换方案2.微服务vnode 替换方案3.每个微服务都不卸载微服务加载方式的选择微服务的路由路径选择微服务的缓存工具微服务的容器使用tab作为微服务的挂载容器使用微服务路由作为微服务的挂载容器场景描述微服…...

2|电子技术|数字电子技术基础|雨课堂习题|考前回顾
A/DD/A转化横向与阵列 相乘,竖向为或阵列 相加!功率放大电路克服交越失真,是在乙类的基础上增加两个二极管,使微导通,使三极管导通时间大于半个周期,小于一个周期,构成甲乙类工作状态。选择填空…...

vue+echarts:圆形柱状图设置角度和最大值
第020个点击查看专栏目录本示例是显示圆形的柱状图,angleAxis设置一个max, angleAxis上startAngle:90 , 将0点设置为最顶点。 文章目录示例效果示例源代码(共100行)相关资料参考专栏介绍示例效果 示例源代码…...

Linux系统安装Nginx常见报错问题
安装Nginx从nginx官网下载所需版本的nginx,http://nginx.org/下载之后,将安装包上传到linux系统指定路径解压文件,tar -zxvf nginx-1.22.1.tar.gz (此处用1.22.1版本为例)进入安装包目录,cd nginx-1.22.1执…...

按下按键之后,打印一句话------>三个按键需要实现
main.c: #include "key.h" extern void printf(const char *fmt, ...); void delay_ms(int ms){ int i,j; for(i 0; i < ms;i) for (j 0; j < 1800; j);} int main(){ //key1键盘 //EXIT控制器初始化 void PF9_exti_init(); //GICD控…...

Mac配置VScode
Mac配置VScode 常用技巧 命令调色板 根据您当前的上下文访问所有可用的命令。 键盘快捷键:⇧⌘P 快速打开 快速打开文件。 键盘快捷键:⌘P **提示:**类型?查看命令建议。 在最近打开的文件夹和工作区之间导航 最近打开 键盘快捷…...
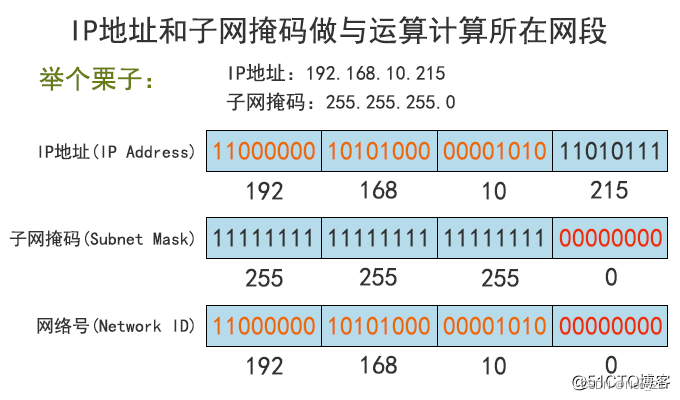
MAC地址IP地址 端口
网络结构: 服务器-客户机(C/S)Client-Server结构,如QQ,LOL都拥有客户端 优点:响应速度快,形式多样,安全新较高缺点:安装软件和维护,不能跨平台LINUX/windows/MAC浏览器-…...

关于虚拟数字人你想知道的都在这里
2022年底,微软旗下的人工智能实验室Open AI发布的对话式大型语言模型ChatGPT聊天机器人一夜蹿红,5天用户量超百万,在各大中外媒体平台掀起了一阵热潮。也带火了人工智能相关产业,AI虚拟数字人就是其中之一,一个随着元宇…...

分布式任务调度处理方案(无代码)
业务涉及到,需要向数据库、redis、elasticsearch、MinIO写四份数据,这里存在分布式事务问题。如何解决问题,先分析cap,是要保证可用性,还是保证一致性。如何选择是CP还是AP?分析业务场景CP的场景࿱…...
2023年博管办香江学者计划、澳门青年学者开始申报
2023年2月20日,全国博士后管委会办公室官方网站发出了2023年香江学者计划、澳门青年学者计划和博士后国(境)外学术交流项目申报指南,以下知识人网小编仅转载香江学者计划和澳门青年学者计划申报指南并做重点解读。知识人网整理香江…...
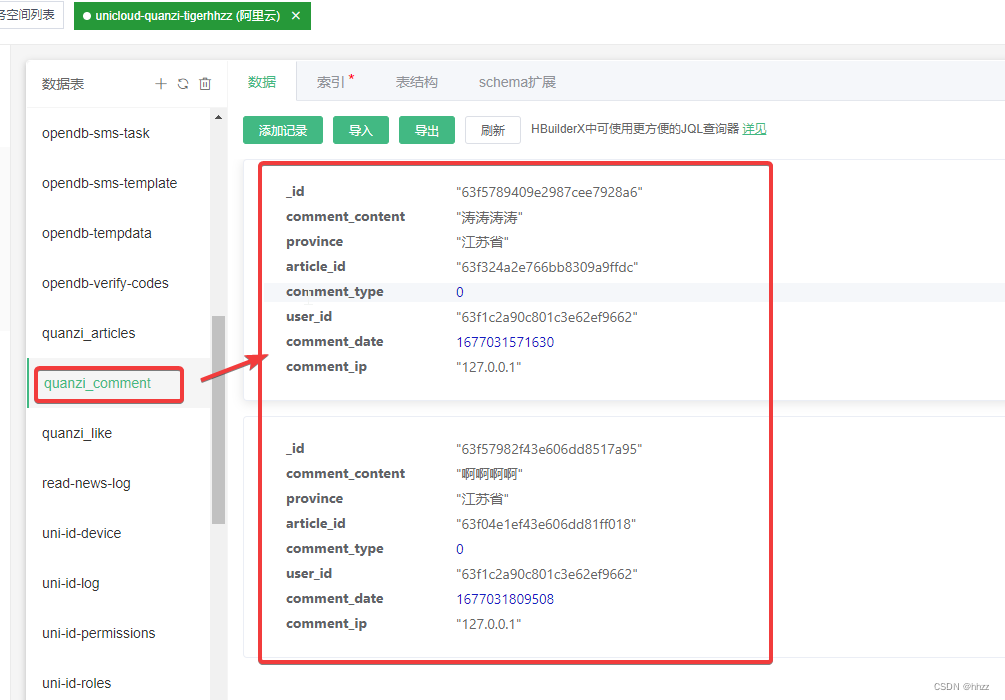
(二十一)、实现评论功能(1)【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,评论回复模块的样式布局 1.1 在detail页面添加uview中的 Empty 内容为空组件 <!-- 评论区 --><view class"comment"><u-empty mode"comment" icon"http://cdn.uviewui.com/uview/empty/comment.png"></u-emp…...
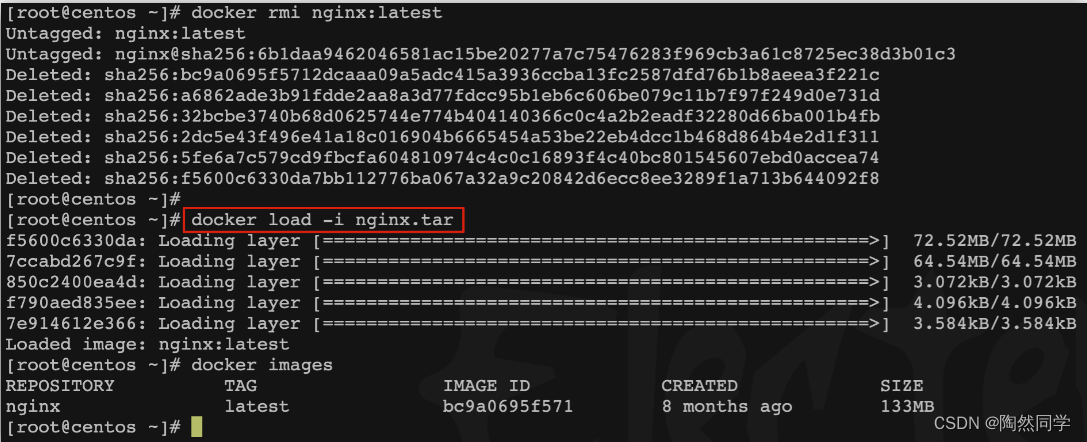
【Docker】初识Dcoker以及镜像操作(一)
目录 1.初识Docker 1.1.什么是Docker 1.1.1.应用部署的环境问题 1.1.2.Docker解决依赖兼容问题 1.1.3.Docker解决操作系统环境差异 1.1.4.小结 1.2.Docker和虚拟机的区别 1.3.Docker架构 1.3.1.镜像和容器 1.3.2.DockerHub 1.3.3.Docker架构 1.3.4.小结 1.4.安装D…...
C#传智:在vs2022中基本了解(第一天))
(1)C#传智:在vs2022中基本了解(第一天)
开始vs2022中C#入门,就是一笔记,算不上原创,没办法得选啊。 一、vs中卸载项目和移除项目有什么区别? 1、卸载、移除都不会移除物理文件,只会删除关联 2、卸载删除关联的程度低,卸载后项目只是“变灰色…...

【数据结构与算法】算法的时间复杂度和空间复杂度
文章目录前言1.算法效率1.1.如何衡量一个算法的好坏1.2.算法的复杂度2.时间复杂度2.1.时间复杂度的概念2.2.大O的渐进表示法2.3.常见时间复杂度计算举例2.4.常见时间复杂度3.空间复杂度4.复杂度oj练习Practice.1 消失的数字Practice.2 旋转数组写在最后前言 关于时空复杂度的分…...

不使用contab -e的方式,添加计划任务
不使用contab -e的方式,添加计划任务 crond 服务的周期任务的文件存放位置在:/var/spool/cron/ 如果你是root用户的话那么你的周期任务文件名就叫root 如果你使用其他用户创建的周期任务,任务文件名就叫它本身 1、 使用root用户创建周期任…...

sentry2摄像头之blink篇
一、硬件 arduino sentry2摄像头 二、实验内容 第一步 安装好esp8266库函数 具体详见ES826安装指导,CSDN有很多资源,或者浏览 https://tosee.readthedocs.io/zh/latest/ 网址 第二步 配置 详情见视频,有简单讲解 视频1:电脑端配置 https://live.csdn.net/v/277427 视频2:s…...

springboot集成PDF导出
内容目录 知识准备 什么是itext itext的历史版本和License问题 标准的itextpdf导出的步骤 实现案例 Pom依赖 导出PDF 添加页眉页脚和水印 进一步理解 遇到license问题怎么办 为何添加页眉页脚和水印是通过PdfPageEvent来完成 除了处理word, excel等文件外,最为常见的…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
