【每日一题】ARC071D - ### | 前缀和 | 简单
题目内容
原题链接
给定一个长度为 n n n 的数组 a a a 和一个长度为 m m m 的数组 b b b 。
从数组 a a a 中挑出两个数,作为两条平行于 y y y 轴的直线,数组 b b b 中挑出两个数,作为两条平行于 x x x 轴的直线,问这四条直线构成的矩形的面积。
你需要所有可能的矩形的面积之和,答案对 1 0 9 + 7 10^9+7 109+7 取模
数据范围
- 2 ≤ n , m ≤ 2 ⋅ 1 0 5 2\leq n,m\leq 2\cdot 10^5 2≤n,m≤2⋅105
- − 1 0 9 ≤ a i , b i ≤ 1 0 9 -10^9\leq a_i,b_i\leq 10^9 −109≤ai,bi≤109
题解
先对两个数组排序,下标从 0 0 0 开始。
对于数组 a a a ,每个数 a i a_{i} ai,考虑比其小的数的和为 p r e a i − 1 prea_{i-1} preai−1,一共有 i i i 个数比 a i a_i ai 小(小于等于),那么和 a i × i − p r e a i − 1 a_i\times i-prea_{i-1} ai×i−preai−1。
对于数组 b b b 也一样。
但是这里需要考虑的是,对于每个数 a i a_i ai ,其需要与数组 b b b 中任意两个数构成的直线进行计算。
所以考虑 p p r e b i = ∑ j = 0 i b i × p r e b i − 1 ppreb_{i}=\sum\limits_{j=0}^i b_i\times preb_{i-1} pprebi=j=0∑ibi×prebi−1
最后答案就是: ∑ i = 0 n − 1 ( a i × i − p r e a i − 1 ) × p p r e b n − 1 \sum\limits_{i=0}^{n-1} (a_i\times i-prea_{i-1})\times ppreb_{n-1} i=0∑n−1(ai×i−preai−1)×pprebn−1
时间复杂度: O ( n ) O(n) O(n)
代码
#include <bits/stdc++.h>
using namespace std;typedef long long ll;const int MOD = 1e9 + 7;int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;vector<ll> a(n), b(m);for (int i = 0; i < n; ++i) cin >> a[i];for (int i = 0; i < m; ++i) cin >> b[i];sort(a.begin(), a.end());sort(b.begin(), b.end());ll prea = (a[0] % MOD + MOD) % MOD;ll preb = (b[0] % MOD + MOD) % MOD, ppreb = 0;for (int i = 1; i < m; ++i) {ppreb += b[i] * i - preb;ppreb = (ppreb % MOD + MOD) % MOD;preb += b[i];preb %= MOD;}ll ans = 0;for (int i = 1; i < n; ++i) {ll cur = ((a[i] * i - prea) % MOD + MOD) % MOD;ans = (ans + cur * ppreb % MOD) % MOD;prea += a[i];prea %= MOD;}cout << ans << "\n";return 0;
}
相关文章:

【每日一题】ARC071D - ### | 前缀和 | 简单
题目内容 原题链接 给定一个长度为 n n n 的数组 a a a 和一个长度为 m m m 的数组 b b b 。 从数组 a a a 中挑出两个数,作为两条平行于 y y y 轴的直线,数组 b b b 中挑出两个数,作为两条平行于 x x x 轴的直线,问这四…...
VueRouter)
(Vue2)VueRouter
VueRouter 修改地址栏路径时,切换显示匹配的组件 使用52: 1下载版本3.6.5(Vue3对应版本4.X) npm add vue-router3.6.5 2引入 import VueRouter from vue-router 3安装注册 Vue.use(VueRouter) 4创建路由对象 const route…...

6.文本注释方法
1.单行注释 在 LaTeX 中,可以使用 % 符号进行单行注释。 2.整段的注释 但如果要注释一整段文字,可以使用 comment 宏包或 \iffalse 和 \fi 命令来实现。 2.1 使用 comment 宏包 在导言区使用 \usepackage{comment} 命令加载 comment 宏包。然后&…...
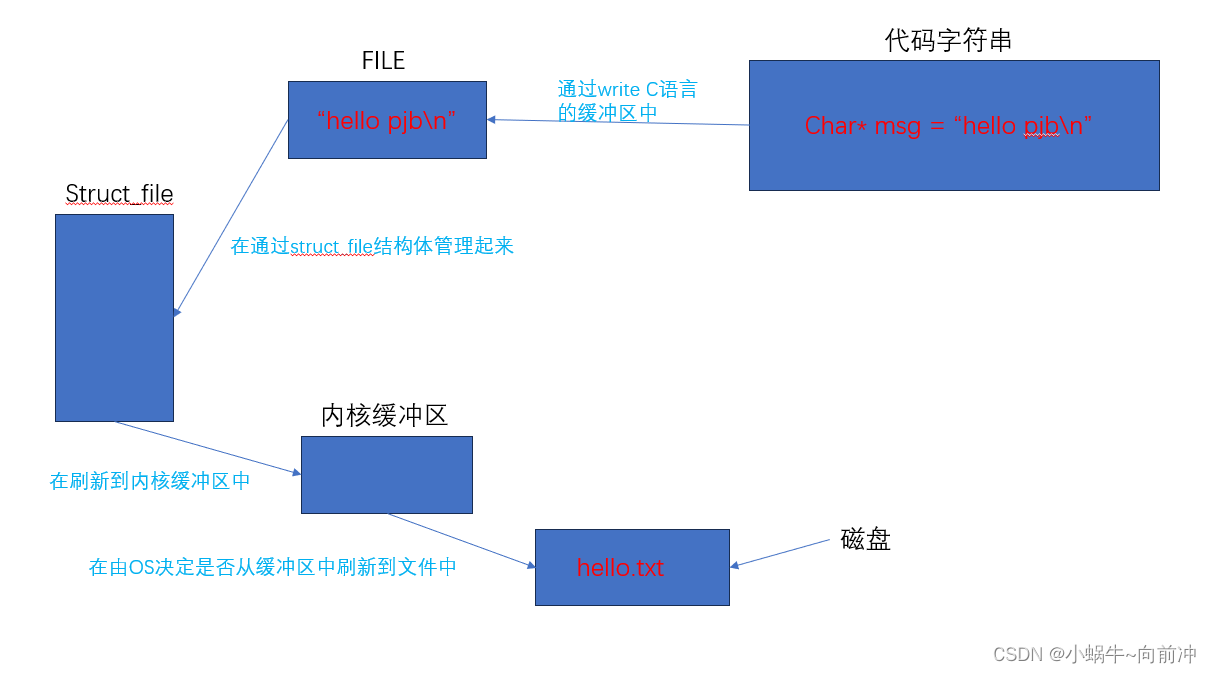
[Linux打怪升级之路]-缓冲区
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 本期学习目标&…...

【力扣】13. 罗马数字转整数
题目描述 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符数值I1V5X10L50C100D500M1000 例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X II 。 27 写…...
高效时间管理,事无巨细掌握——OmniFocus Pro 3 for Mac最强GTD工具
在快节奏的现代生活中,有效地管理和安排时间变得至关重要。如果您正在寻找一款功能强大的时间管理工具,那么OmniFocus Pro 3 for Mac将是您的最佳选择。作为一款专业的GTD(Getting Things Done)应用程序,它为您提供了一…...

解锁前端Vue3宝藏级资料 第五章 Vue 组件应用 3( Slots )
5.4 Slots 我们已经了解到组件能够接收任意类型的 JavaScript 值作为 props,但组件要如何接收模板内容呢?在某些场景中,我们可能想要为子组件传递一些模板片段,让子组件在它们的组件中渲染这些片段。Slots 可用于将Html内容从父组…...

接口测试之文件上传
在日常工作中,经常有上传文件功能的测试场景,因此,本文介绍两种主流编写上传文件接口测试脚本的方法。 首先,要知道文件上传的一般原理:客户端根据文件路径读取文件内容,将文件内容转换成二进制文件流的格…...

7.Flask-Migrate数据库迁移
基本介绍 flask-migrate是基于Alembic的一个封装,并集成到Flask中 所有的迁移操作其实都是Alembic做的,能跟踪模型的变化,并将变化映射到数据库中 一.安装 pip install flask-migrate二.基本使用 2.1初始化数据库迁移脚本 在Flask应用的根目录下,运行命令 flas…...
信创办公–基于WPS的PPT最佳实践系列 (项目8创建电子相册)
信创办公–基于WPS的PPT最佳实践系列 (项目8创建电子相册) 目录 应用背景操作步骤 应用背景 如果我们想把图片弄成相册,或者弄成一段有音乐的视频分享给朋友。我们可以利用PPT来制作。那我们如何用PPT制作电子相册或视频呢?可以跟…...
JRedis的基本操作,基本数据类型操作
Redis的基本数据类型: stringhashlistsetzset {public static void main(String[] args) {Jedis jedis new Jedis("127.0.0.1", 6379);// stringjedis.set("hello", "word");String hello jedis.get("hello");System.o…...

QT网页 webengine / CEF
QT WebEngine 官方文档 WebEngine 架构: 能看到 WebEngine 有一个核心模块是基于 Chromium 构造的,通过使用 Chromium 的Blink渲染引擎和V8 JavaScript引擎来处理和渲染Web内容,并将这些底层技术封装为一系列高级的C类和接口,以…...

Golang笔试题:编写一个函数,接收一个整数参数n,输出n的阶乘结果
今天,我们开发的AI笔试题工具,ai扁食——AI程序员笔试系统给我出了中级Golang题目,就是这道题:《请编写一个函数,接收一个整数参数n,输出n的阶乘结果》,希望我写一个函数,输出n的阶乘…...
外包干了2个月,技术退步明显.......
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

无涯教程-JavaScript - BINOM.DIST函数
描述 BINOM.DIST函数返回单个项二项式分布概率。 在具有固定数量的测试或试验的问题中使用BINOM.DIST。 当任何试验的输出只是成功或失败时 试验是独立的,并且 在整个实验中成功的概率不变的情况 语法 BINOM.DIST (number_s,trials,probability_s,cumulative)争论 Argu…...

linux定时重启tomcat
1.编辑重启Tomcat命令 首先编辑一个文件 vi my_restart.sh 然后输入: #!/bin/bash . /etc/profile tomcatPath"/opt/finereport/tomcat" binPath"$tomcatPath/bin" echo "[info][$(date %F %H:%M:%S)]正在监控tomcat,路径&a…...

在静态方法中访问@Value注入的静态变量!!
一、 静态变量 static修饰的成员变量,称为静态成员变量,静态成员变量最大的特性:不属于某个具体的对象,是所有对象所共享的 简单来说:在某些类的对象中存在一些相同的成员变量,那么这种成员变量就可以设置…...

掌握这些算法,让你的编程之路更顺畅——重要算法解析
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。这些算法通常被广泛应用于日常编程工作中,是提升编程效率和解决实际问题的重要工具。本文将介绍几种十分重要的“必抓…...
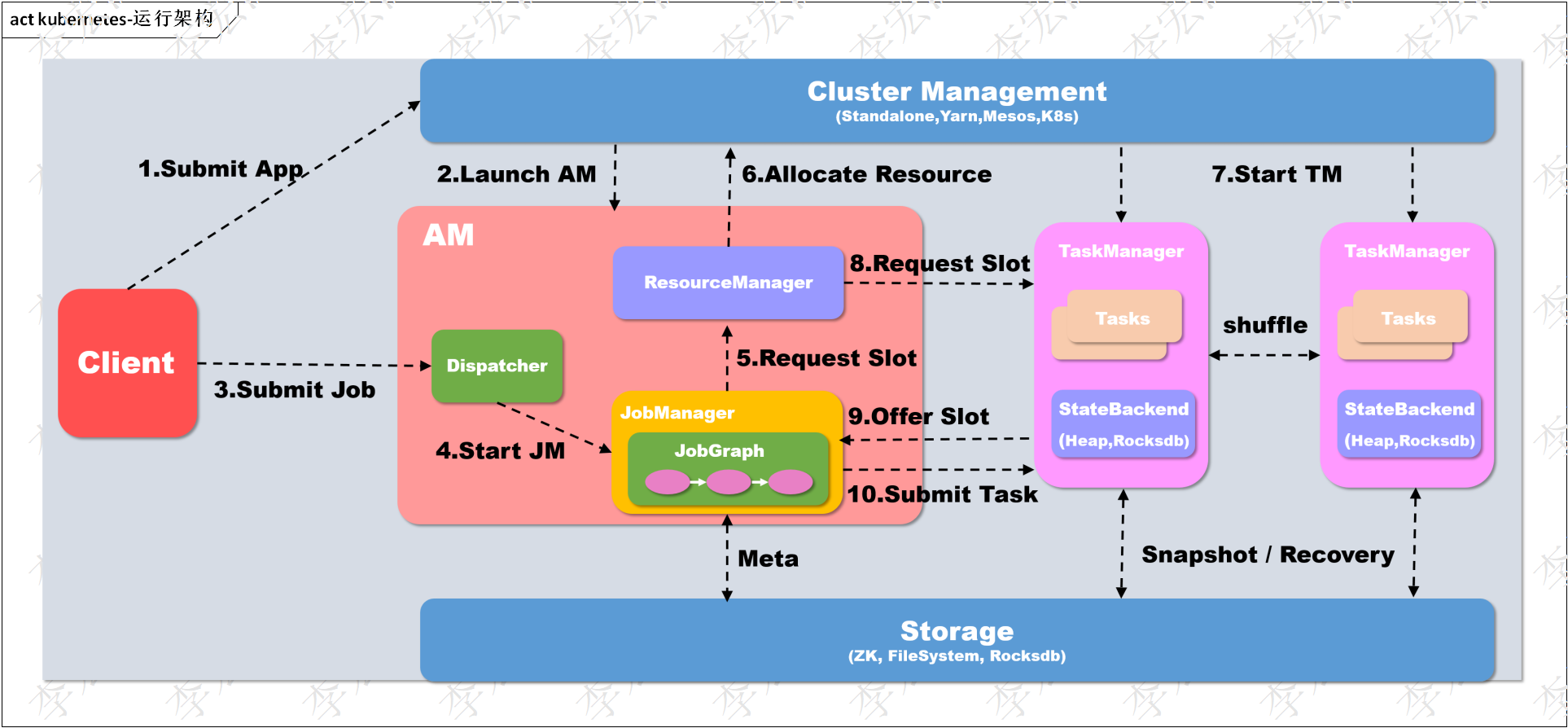
flink集群与资源@k8s源码分析-总述
1 简介 集群和资源模块提供动态资源能力,是分布式系统关键基础设施,分布式datax,分布式索引,事件引擎都需要集群和资源的弹性资源能力,提高伸缩性和作业处理能力。本文分析flink的集群和资源的k8s模块,深入了解其设计原理,为开发自有的集群和资源组件做技术准备, 同时涉…...

LeetCode 0213. 打家劫舍 II:动动态规划
【LetMeFly】213.打家劫舍 II:动动态规划 力扣题目链接:https://leetcode.cn/problems/house-robber-ii/ 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
