LC1713. 得到子序列的最少操作次数(java - 动态规划)
LC1713. 得到子序列的最少操作次数
- 题目描述
- LIS 动态规划 + 二分法
- 代码演示
题目描述
难度 - 困难
LC1713.得到子序列的最少操作次数
给你一个数组 target ,包含若干 互不相同 的整数,以及另一个整数数组 arr ,arr 可能 包含重复元素。
每一次操作中,你可以在 arr 的任意位置插入任一整数。比方说,如果 arr = [1,4,1,2] ,那么你可以在中间添加 3 得到 [1,4,3,1,2] 。你可以在数组最开始或最后面添加整数。
请你返回 最少 操作次数,使得 target 成为 arr 的一个子序列。
一个数组的 子序列 指的是删除原数组的某些元素(可能一个元素都不删除),同时不改变其余元素的相对顺序得到的数组。比方说,[2,7,4] 是 [4,2,3,7,2,1,4] 的子序列(加粗元素),但 [2,4,2] 不是子序列。
示例 1:
输入:target = [5,1,3], arr = [9,4,2,3,4]
输出:2
解释:你可以添加 5 和 1 ,使得 arr 变为 [5,9,4,1,2,3,4] ,target 为 arr 的子序列。
示例 2:
输入:target = [6,4,8,1,3,2], arr = [4,7,6,2,3,8,6,1]
输出:3
提示:
1 <= target.length, arr.length <= 10^5
1 <= target[i], arr[i] <= 10^9
target 不包含任何重复元素。
LIS 动态规划 + 二分法
为了方便,我们令 target 长度为 n,arr 长度为 m,target 和 arr 的最长公共子序列长度为 max,不难发现最终答案为 n−max。
因此从题面来说,这是一道最长公共子序列问题(LCS)。
但朴素求解 LCS 问题复杂度为 O(n∗m),使用状态定义「f[i][j] 为考虑 a 数组的前 i 个元素和 b 数组的前 j 个元素的最长公共子序列长度为多少」进行求解。
而本题的数据范围为 10^5,使用朴素求解 LCS 的做法必然超时。
一个很显眼的切入点是 target 数组元素各不相同,当 LCS 问题增加某些条件限制之后,会存在一些很有趣的性质。
其中一个经典的性质就是:当其中一个数组元素各不相同时,最长公共子序列问题(LCS)可以转换为最长上升子序列问题(LIS)进行求解。同时最长上升子序列问题(LIS)存在使用「维护单调序列 + 二分」的贪心解法,复杂度为 O(nlogn)。
因此本题可以通过「抽象成 LCS 问题」->「利用 target数组元素各不相同,转换为 LIS 问题」->「使用 LIS 的贪心解法」,做到 O(nlogn) 的复杂度。
朴素的 LIS 问题求解,我们需要定义一个 f[i] 数组代表以 nums[i] 为结尾的最长上升子序列的长度为多少。
对于某个 f[i] 而言,我们需要往回检查 [0,i−1] 区间内,所有可以将 nums[i] 接到后面的位置 jjj,在所有的 f[j]+1中取最大值更新 f[i]。因此朴素的 LIS 问题复杂度是 O(n^2) 的。
LIS 的贪心解法则是维护一个额外 ggg 数组,g[len]=x 代表上升子序列长度为 lenlenlen 的上升子序列的「最小结尾元素」为 x。
整理一下,我们总共有两个数组:
- f 动规数组:与朴素 LIS 解法的动规数组含义一致。f[i]f[i]f[i] 代表以 nums[i] 为结尾的上升子序列的最大长度;
- g 贪心数组:g[len]=x代表上升子序列长度为 len 的上升子序列的「最小结尾元素」为 x。
由于我们计算 f[i] 时,需要找到满足 nums[j]<nums[i],同时取得最大 f[j] 的位置 j。
我们期望通过 g 数组代替线性遍历。
显然,如果 g 数组具有「单调递增」特性的话,我们可以通过「二分」找到符合 g[idx]<nums[i] 分割点 idxi(下标最大),即利用 O(logn) 复杂度找到最佳转移位置。
代码演示
class Solution {public int minOperations(int[] target , int[] arr) {Map<Integer, Integer> map = new HashMap();int Tlen = target.length, Alen = arr.length;//1:target的元素和对应下标 装入mapfor(int i = 0; i < Tlen; i++) map.put(target[i], i);//2:在arr中寻找相等的值的下标装入下标数组int[] index = new int[Alen];int p = 0;for(int i = 0; i < Alen; i++){if(map.containsKey(arr[i])) index[p++] = map.get(arr[i]);}//3:直接调用处理最长递增公共子串代码(之前做过,这里赋值过来,偷懒)int uplen = lengthOfLIS(index,p);return Tlen - uplen;}public int lengthOfLIS(int[] nums,int n){if(n == 0) return 0;int res = 1;int[] dp = new int[n];dp[0] = nums[0];for(int num:nums){int i = 0,j = res;while(i < j){int mid = (i + j)>>1;if(dp[mid] >= num) j = mid;else i = mid + 1;}dp[i] = num;if(j == res) res++;}return res;}}
相关文章:

LC1713. 得到子序列的最少操作次数(java - 动态规划)
LC1713. 得到子序列的最少操作次数 题目描述LIS 动态规划 二分法代码演示 题目描述 难度 - 困难 LC1713.得到子序列的最少操作次数 给你一个数组 target ,包含若干 互不相同 的整数,以及另一个整数数组 arr ,arr 可能 包含重复元素。 每一次…...
vr飞机驾驶舱模拟流程3D仿真演示加大航飞安全法码
众所周知,航空航天飞行是一项耗资大、变量参数很多、非常复杂的系统工程,因此可利用虚拟仿真技术经济、安全及可重复性等特点,进行飞行任务或操作的模拟,以代替某些费时、费力、费钱的真实试验或者真实试验无法开展的场合…...
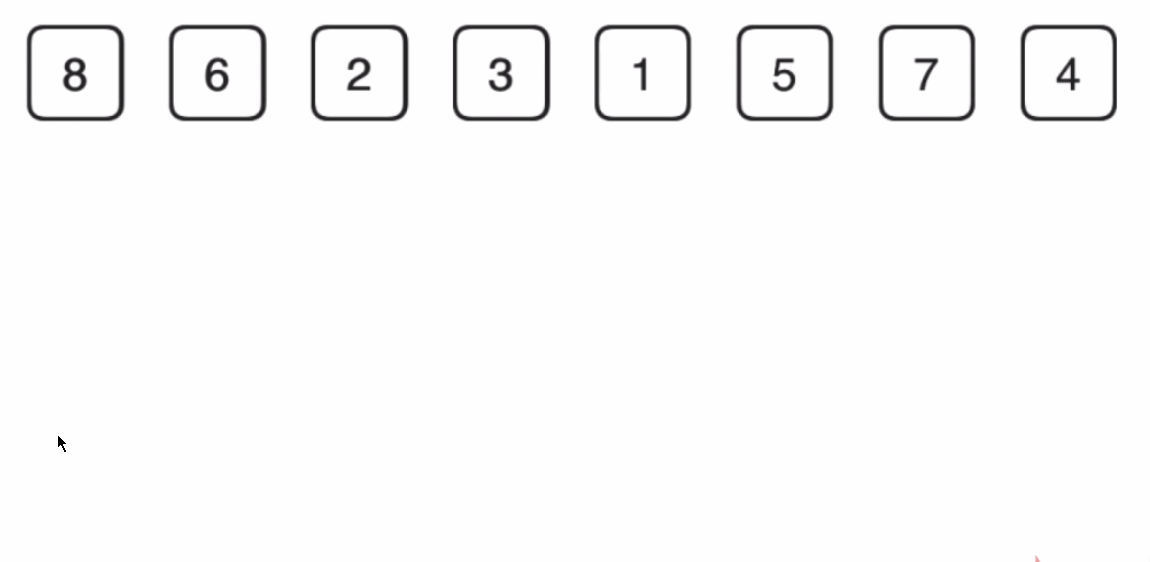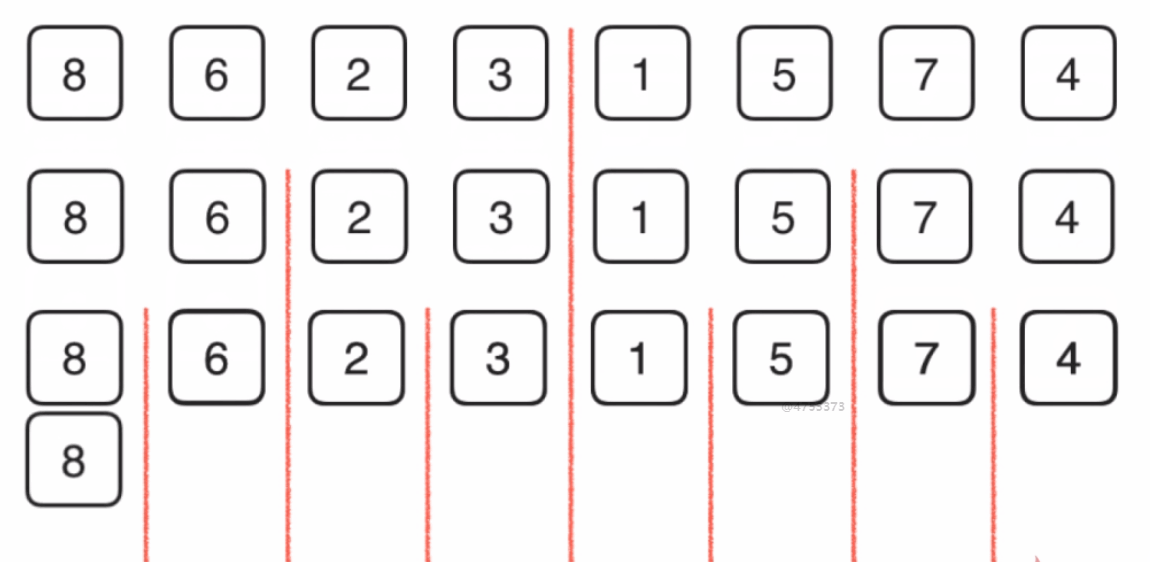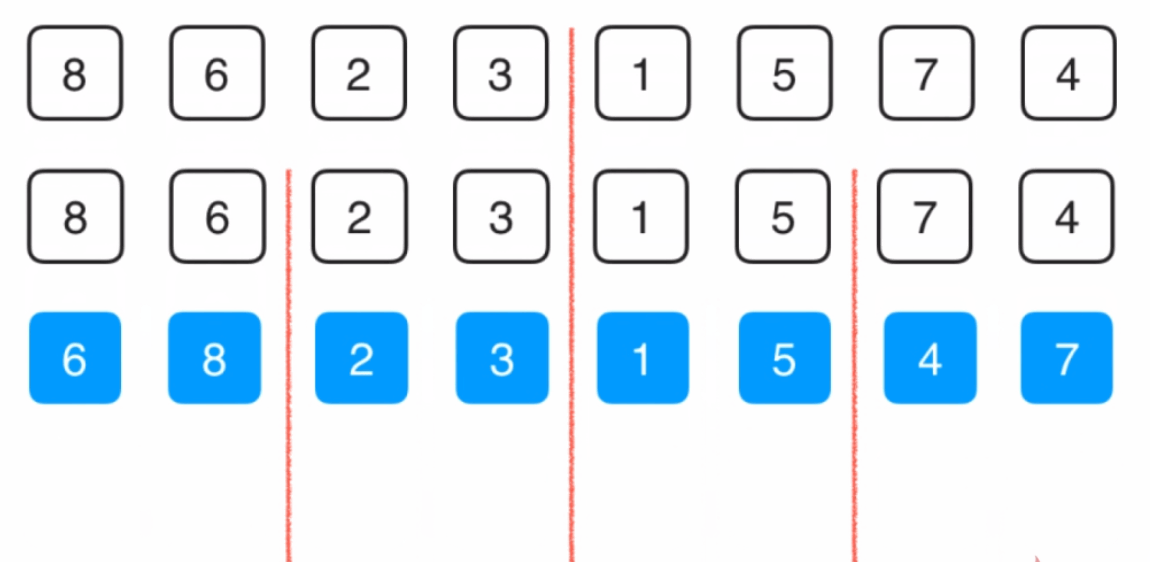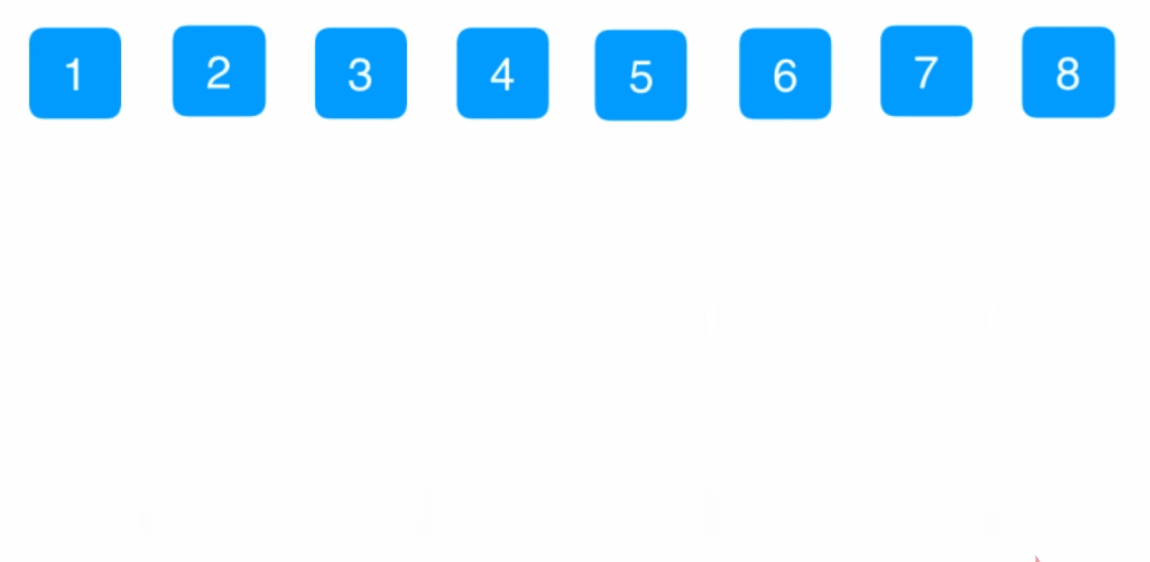
一、八大排序(sort)
文章目录 一、时间复杂度(一)定义:常数操作 二、空间复杂度(一)定义: 三、排序(一)选择排序1.定义2.代码3.特性 (二)冒泡排序1.定义2.代码3.特性 (…...
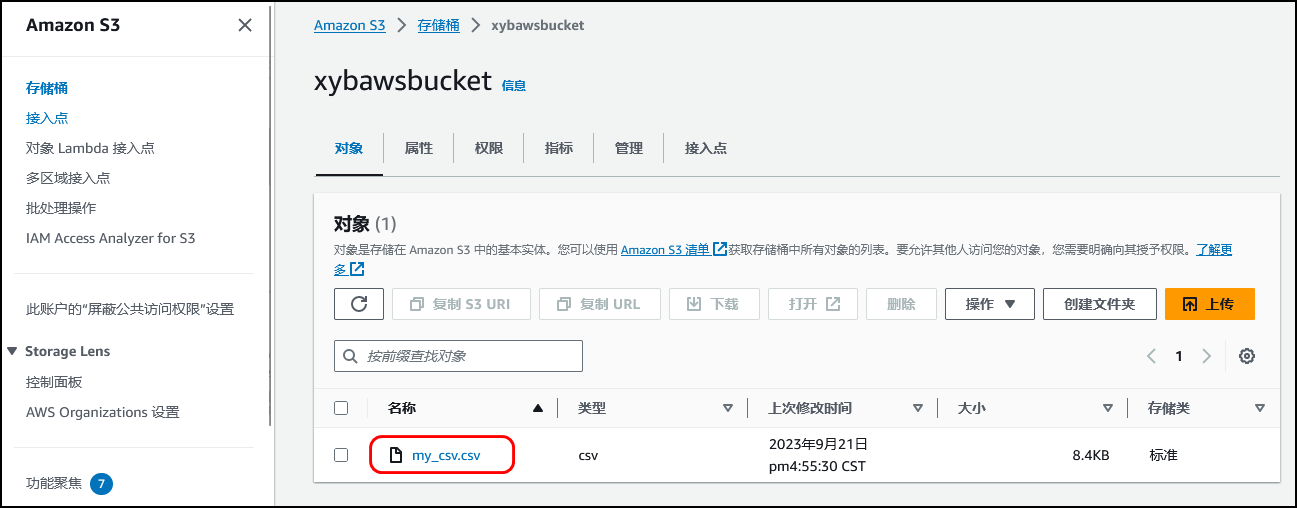
【AWS】AI 代码生成器—Amazon CodeWhisperer初体验 | 开启开挂编程之旅
使用 AI 编码配套应用程序更快、更安全地构建应用程序 文章目录 1.1 Amazon CodeWhisperper简介1.2 Amazon CodeWhisperer 定价2.1 打开VS Code2.2 安装AWS ToolKit插件 一、前言 1.1 Amazon CodeWhisperper简介 1️⃣更快地完成更多工作 CodeWhisperer 经过数十亿行代码的训…...

【Mysql主从配置方法---单主从】
Mysql主从 主服务器 创建用户 create user “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 授权 grant replication slave on . to “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 查看用户权限 SHOW GRANTS FOR “for_rep”“从服务器IP地址”; 修改M…...

⼀⽂读懂加密资产交易赛道的新锐⼒量Bitdu
交易所,仍然是加密资产赛道的皇冠级赛道。围绕这个领域展开的商业竞争,最能引起⼴⼤⽤⼾的关注。 经历了数轮资产价格涨跌的⽜熊之后,⼀批批创业者也在不断地思考这⼀议题 — 如何在去中⼼化的世界中,最⾼效率地集结流量、资本和…...
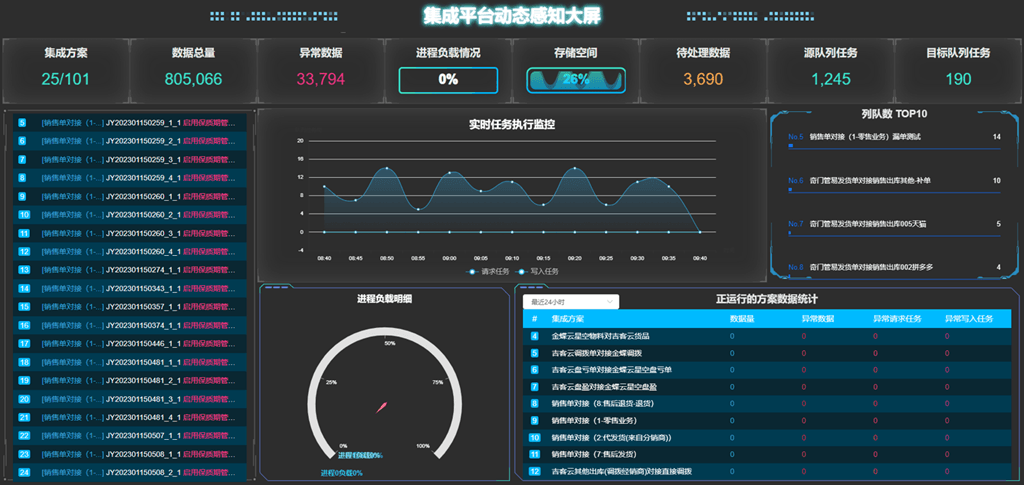
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】)
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】) 源系统:万里牛 万里牛是杭州湖畔网络技术有限公司旗下SaaS软件品牌,主要针对电商、外贸、实体门店等业务群体,帮助企业快速布局新零售,提升订单处理效…...
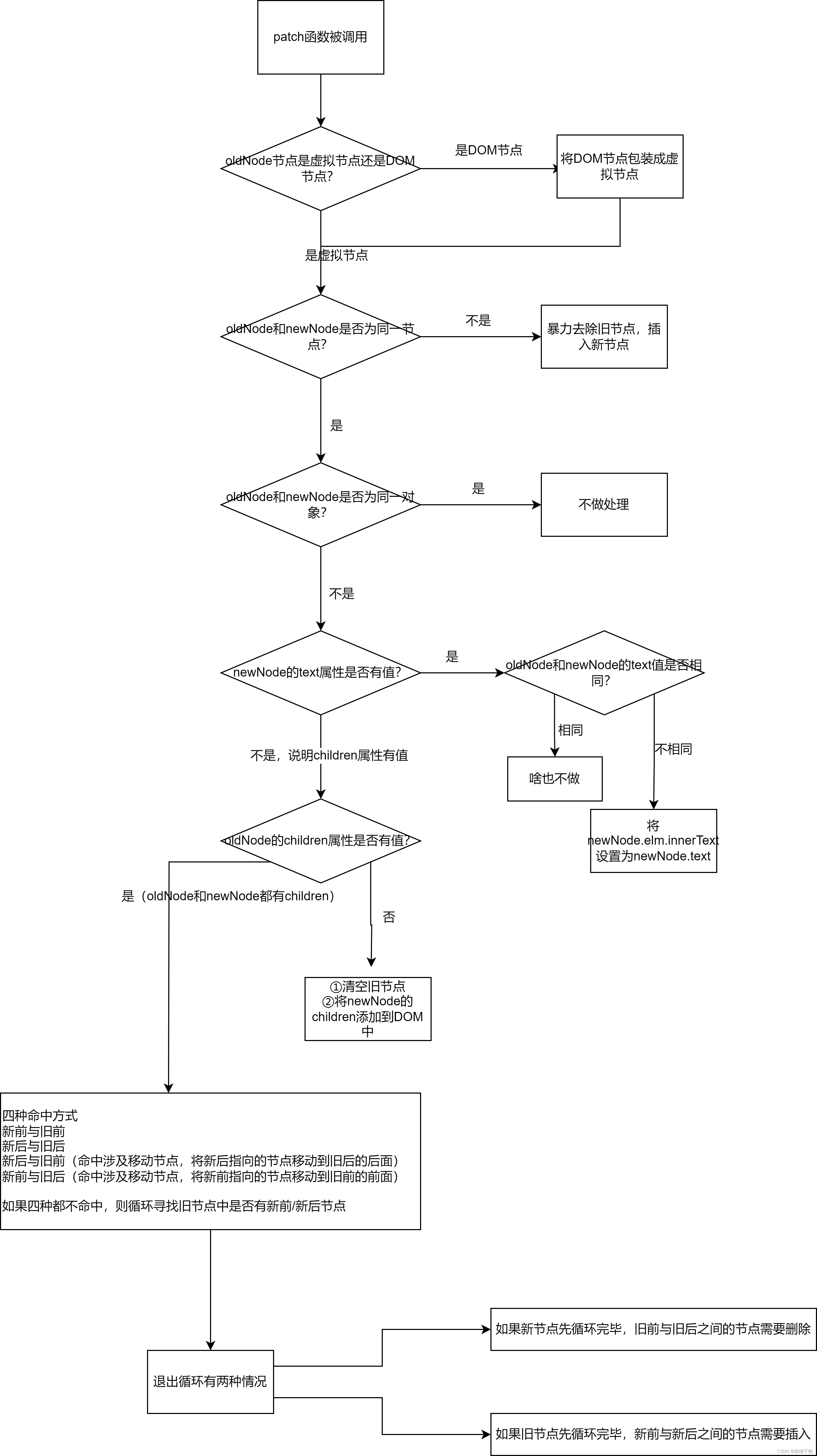
虚拟DOM与diff算法
虚拟DOM与diff算法 snabbdom虚拟DOMdiff算法 snabbdom 是什么:snabbdom是著名的虚拟DOM库,是diff算法的鼻祖,Vue源码借鉴了snabbdom 虚拟DOM 是什么:本质上是存在内存里的 JavaScript 对象 作用:用来描述真实DOM的层…...

K8S:pod资源限制及探针
文章目录 一.pod资源限制1.pod资源限制方式2.pod资源限制指定时指定的参数(1)request 资源(2) limit 资源(3)两种资源匹配方式 3.资源限制的示例(1)官网示例(2࿰…...

CSS中的定位
position 的属性与含义 CSS 中的 position 属性用于控制元素在页面中的定位方式,有四个主要的取值,每个取值都会影响元素的布局方式,它们是: static(默认值): 这是所有元素的初始定位方式。在静…...
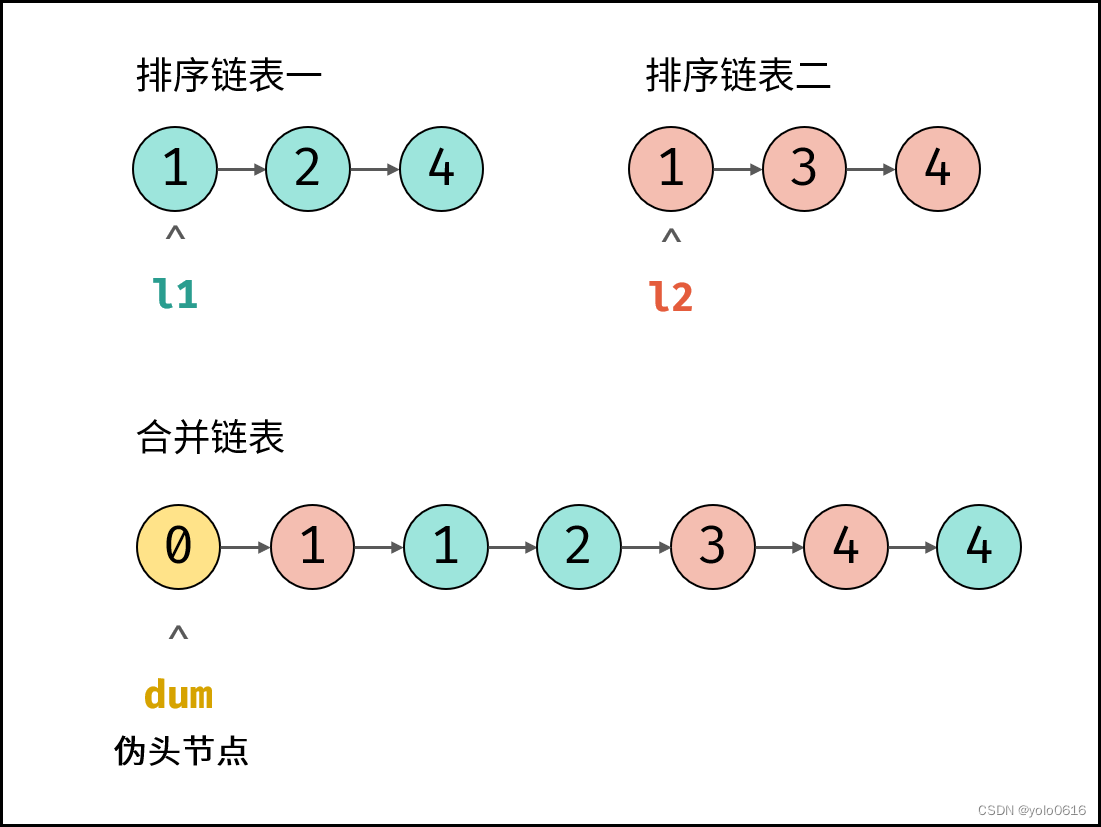
二、链表(linked-list)
文章目录 一、定义二、经典例题(一)[21.合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)1.思路2.复杂度分析3.注意4.代码 (二)[86.分割链表](https://leetcode.cn/problems/partition-list…...
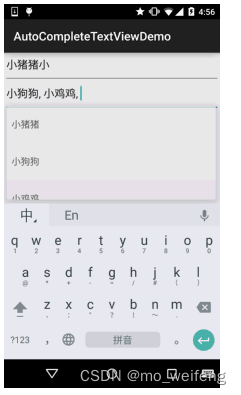
Android EditText筛选+选择功能开发
在日常开发中经常会遇到这种需求,EditText既需要可以筛选,又可以点击选择。这里筛选功能用的是AutoCompleteTextView,选择功能使用的是第三方库https://github.com/kongzue/DialogX。 Android AutoCompleteTextView(自动完成文本框)的基本使用…...

Linux 信号 alarm函数 setitimer函数
/*#include <unistd.h>unsigned int alarm(unsigned int seconds);功能:设置定时器。函数调用,开始倒计时,0的时候给当前的进程发送SIGALARM信号参数:倒计时的时长。。单位:秒 如果参数为0,无效返回…...

自主设计,模拟实现 RabbitMQ - 实现发送方消息确认机制
目录 一、实现发送方消息确认 1.1、需求分析 什么是发送方的消息确认? 如何实现?...

【数据结构】二叉树的·深度优先遍历(前中后序遍历)and·广度优先(层序遍历)
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
优彩云采集器下载-免费优彩云采集器下载地址
免费优彩云采集器。您是否曾为了数据采集而感到头疼不已?是否一直在寻找一种能够轻松、高效地获取所需数据的方法?别着急,让我们一起来了解如何通过优彩云采集器解决这些问题,从而让您产生购买的欲望。 免费全自动采集发布批量管理…...

【Python】OJ 常用函数
这里写目录标题 一. math1. 求阶乘 - factorial()2. 绝对值 - fabs() 二. 容器的方法1. reverse() 三. Python 内置函数1. sort() 一. math 需要引入 math 包:import math 1. 求阶乘 - factorial() import math print(math.factorial(5))--------运行结果-------…...

【Vue】上万个字把事件处理讲解的淋漓尽致
hello,我是小索奇,精心制作的Vue系列教程持续更新哈,想要学习&巩固&避坑就一起学习吧~ 事件处理 事件的基本用法 重点内容 使用v-on:xxx缩写xxx绑定事件,其中 xxx 是事件名(回顾:v-bind缩写为冒号…...

Remmina中VNC、SSH和RDP的区别
Remmina 可以在 Linux 系统上对远程进行连接。它支持多种远程连接协议,包括 VNC(Virtual Network Computing)、SSH(Secure Shell)和 RDP(Remote Desktop Protocol)。这些协议用于实现不同类型的…...
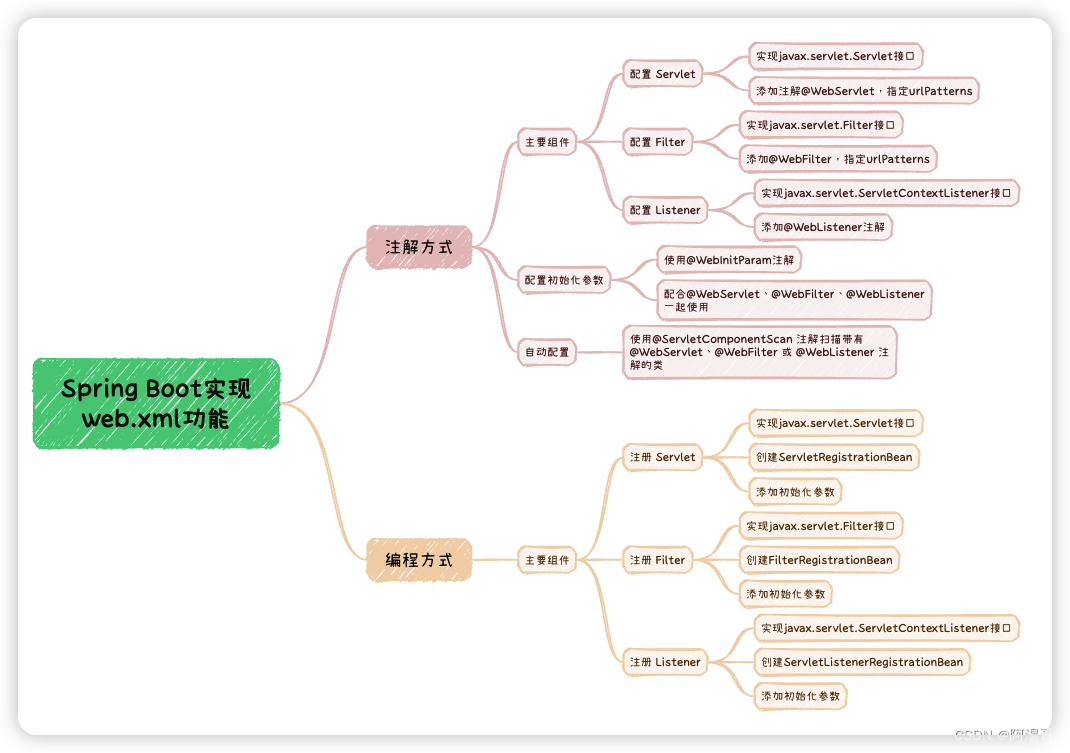
Spring Boot实现web.xml功能
Spring Boot实现web.xml功能 1. 基于注解实现1.1 组件注册1.2 WebInitParam注解 2. 基于编码实现2.1 Servlet & Filter2.2 Listener 3. 总结 在Spring Boot中,不再需要使用传统的 web.xml 文件来配置web应用的功能,Spring Boot支持通过注解和基于代码…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
