2023年浙工商MBA新生奖学金名单公布,如何看待?
浙工商MBA项目官方最新公布了2023年的非全日制新生奖学金名单,按照政策约定,共分为特等奖学金1名,一等奖学金10名,二等奖学金15名,三等奖学金30名,额度对应3万、1万、0.8万、0.5万不等,主要名单信息如下:
 2023浙工商MBA奖学金名单
2023浙工商MBA奖学金名单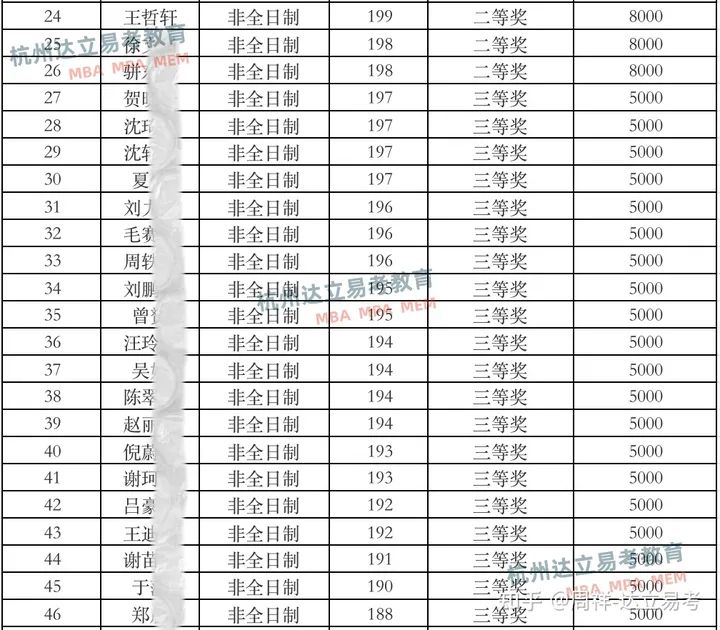 2023浙工商MBA奖学金名单
2023浙工商MBA奖学金名单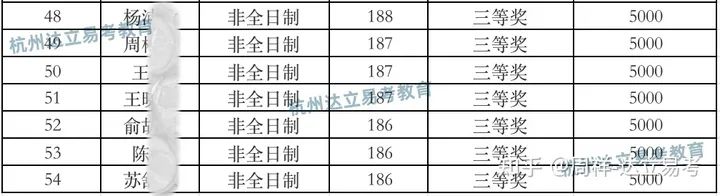 2023浙工商MBA奖学金名单
2023浙工商MBA奖学金名单
浙工商MBA项目2023届的非全日制学费是12.8万,总计招收了207人,预期学费收入约为2650万,本届的非全奖学金总额度为39万,按照比例来说占到1.47%,从这个角度来说确实不是很有冲击力,隔壁的工大MBA奖学金占比大概为1.58%,也没高到哪里去,所以这个比例应该可以理解为目前基本的“市场行情”,对于冲着奖学金读书的考生,参考着一志愿的分数信息还是可以制定一个目标去追求的,毕竟再小的苍蝇也是肉。
从另一个维度来说,浙工商MBA项目的奖学金制度也是从2023届开始的,而且学费的上调也恰恰是这一届,所以从某种意义上来说也可以看作是对涨价后的一种回馈缓冲方式,毕竟作为普通高校MBA项目,以目前的学费水平在全国同类项目中算是偏高的了,只是在江浙长三角地区,考生们的选择余地不大,算是吃了一波地理差异优势的红利。
万了八千的奖学金客观来说对于大多数考生其实吸引力并不是很大,如果一个学员真的是冲着奖学金而去选择了某个项目,站在客观的角度来说对自己的未来也不是很负责任的行为。杭州达立易考教育立足浙江这么多年,每年接触的考生有很多,大多数考生还是在选择项目上花费了不少精力去对比做出决策,经济承受的住的一般首选还是浙大MBA项目,而经济承受不了的,在普通类MBA项目中也会尽量选择更加匹配自己的项目,杭州达立易考教育认为这才是相对客观理性的选择,对自己负责的选择。更多省内MBA项目的选择报考与备考课程指导,可以随时与杭州达立易考教育沟通联系!(专注联考 达立易考)
相关文章:

2023年浙工商MBA新生奖学金名单公布,如何看待?
浙工商MBA项目官方最新公布了2023年的非全日制新生奖学金名单,按照政策约定,共分为特等奖学金1名,一等奖学金10名,二等奖学金15名,三等奖学金30名,额度对应3万、1万、0.8万、0.5万不等,主要名单…...
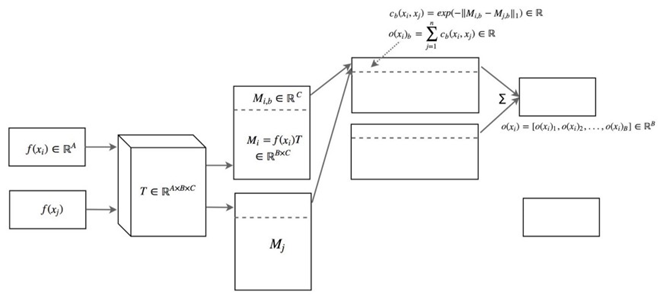
关于时空数据的培训 GAN:实用指南(第 02/3 部分)
一、说明 在本系列关于训练 GAN 实用指南的第 1 部分中,我们讨论了 a) 鉴别器 (D) 和生成器 (G) 训练之间的不平衡如何导致模式崩溃和由于梯度消失而导致静音学习,以及 b) GAN 对超参…...

UNIAPP利用canvas绘制图片和文字,并跟随鼠标移动
最近有个项目,要触摸组件,产生一条图片跟随移动,并显示相应的文字,在网上找了一些资料,终于完成构想,废话少说,直接上代码(测试通过) <template> <view>…...
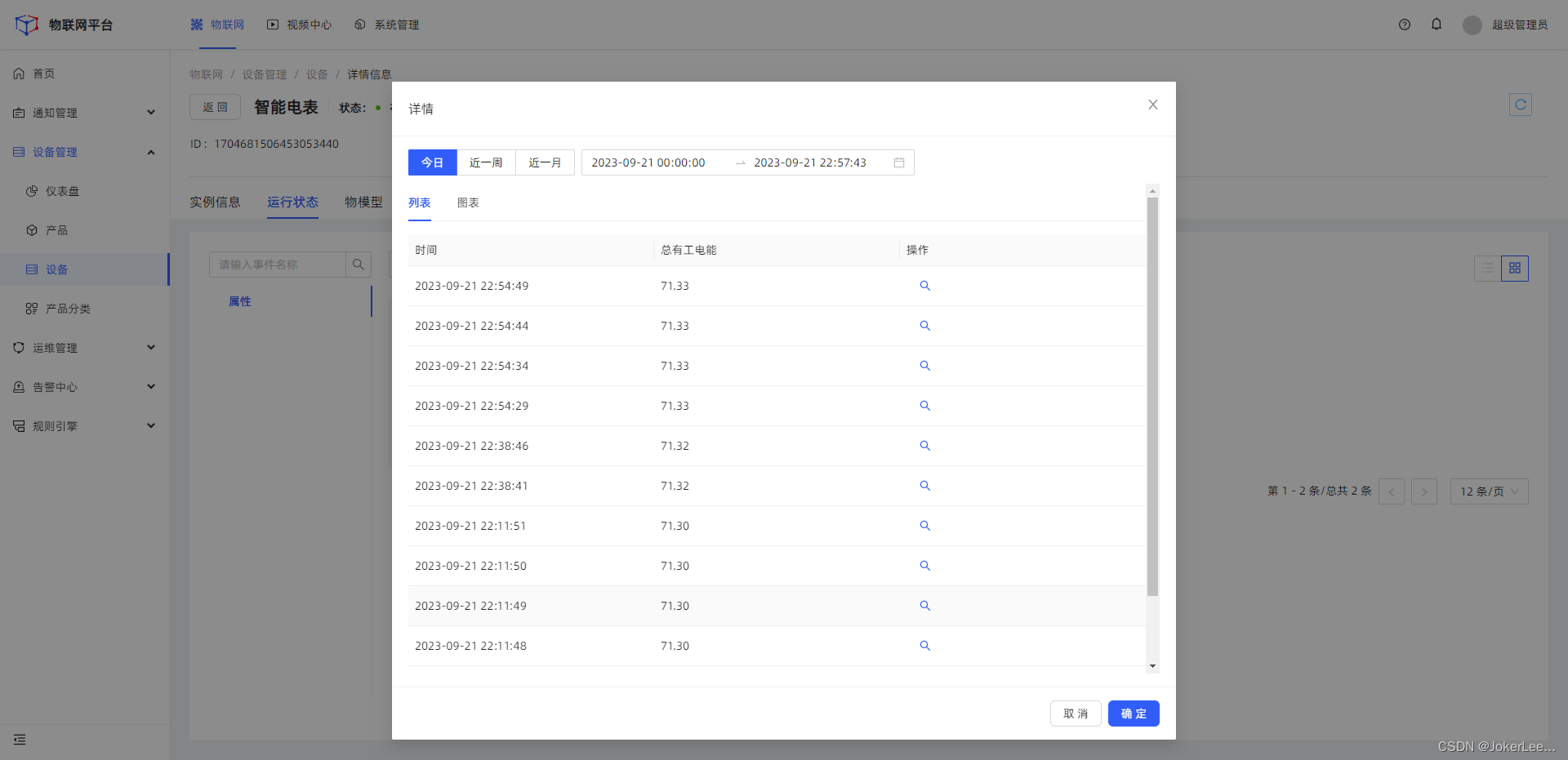
【智能电表数据接入物联网平台实践】
智能电表数据接入物联网平台实践 设备接线准备设备调试代码实现Modbus TCP Client 读取电表数据读取寄存器数据转成32bit Float格式然后使用modbusTCP Client 读取数据 使用mqtt协议接入物联网平台最终代码实现 设备接线准备 设备调试 代码实现 Modbus TCP Client 读取电表数…...

Docker--network命令的用法
原文网址:Docker--network命令的用法_IT利刃出鞘的博客-CSDN博客 简介 说明 本文介绍Docker的network网络命令的用法。 官网网址 docker network | Docker Documentation 命令概述 所有命令 命令名称 说明 docker network connect 将容器连接到网络 dock…...
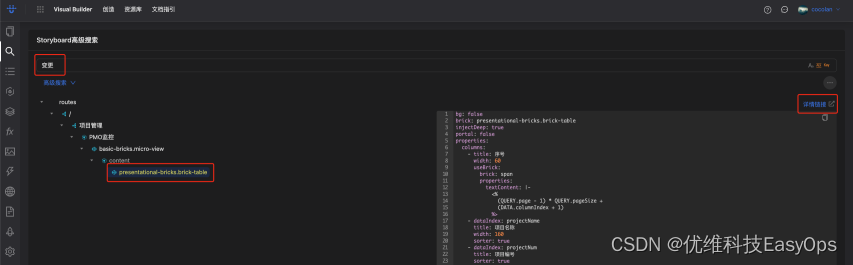
优维低代码实践:图片和搜索
优维低代码技术专栏,是一个全新的、技术为主的专栏,由优维技术委员会成员执笔,基于优维7年低代码技术研发及运维成果,主要介绍低代码相关的技术原理及架构逻辑,目的是给广大运维人提供一个技术交流与学习的平台。 优维…...
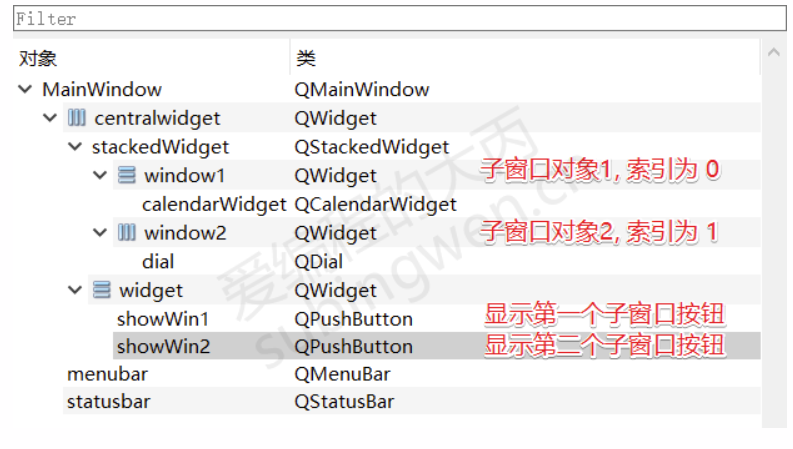
[Qt]控件
文章摘于 爱编程的大丙 文章目录 1. 按钮类型控件1.1 按钮基类 QAbstractButton1.1.1 标题和图标1.1.2 按钮的 Check 属性1.1.3 信号1.1.4 槽函数 1.2 QPushButton1.2.1 常用API1.2.2 按钮的使用 1.3 QToolButton1.3.1 常用API1.3.2 按钮的使用 1.4 QRadioButton1.4.1 常用API…...
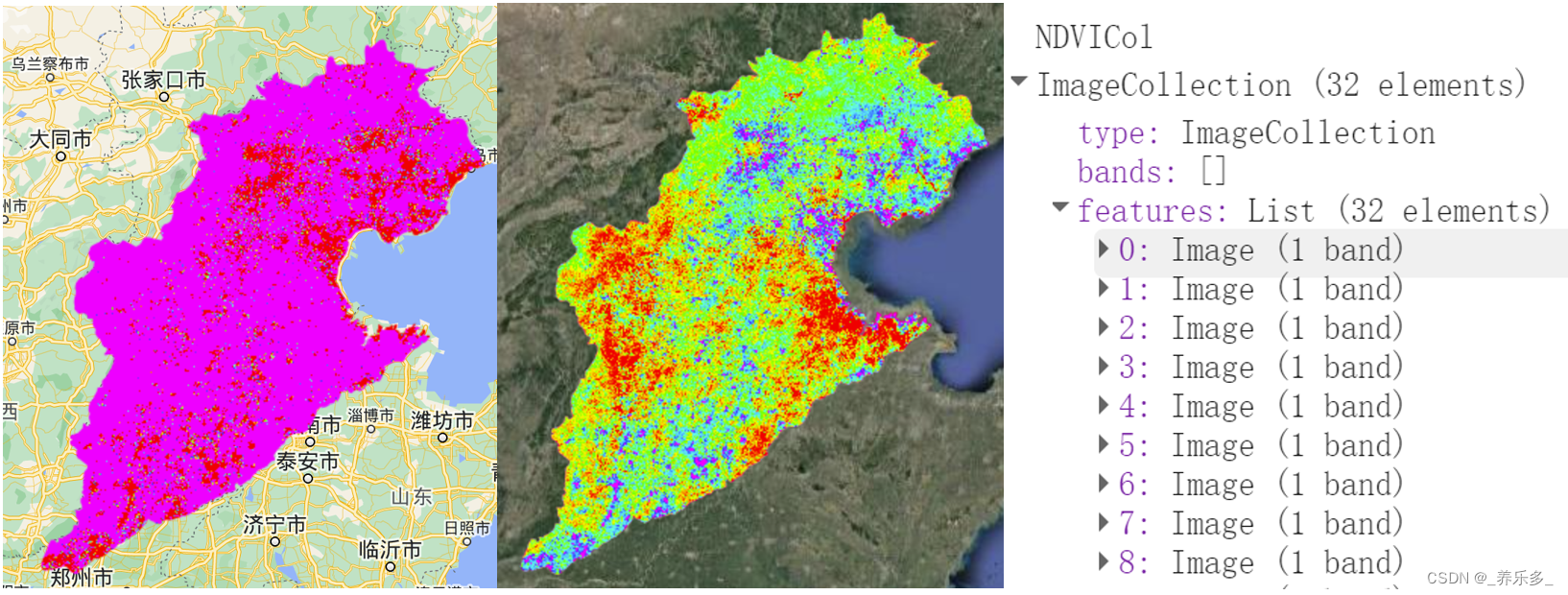
GEE:快速实现时间序列线性趋势和变化敏感性计算(斜率、截距)以NDVI时间序列为例
作者:CSDN @ _养乐多_ 本博客将向您介绍如何使用Google Earth Engine(GEE)平台来处理Landsat 5、7和8的卫星图像数据,构建时间序列,以NDVI为例,计算NDVI时间序列的斜率和截距,以及如何导出这些结果供进一步分析使用。 文章目录 一、代码详解1.1 核心代码详解1.2 核心代…...

LC1713. 得到子序列的最少操作次数(java - 动态规划)
LC1713. 得到子序列的最少操作次数 题目描述LIS 动态规划 二分法代码演示 题目描述 难度 - 困难 LC1713.得到子序列的最少操作次数 给你一个数组 target ,包含若干 互不相同 的整数,以及另一个整数数组 arr ,arr 可能 包含重复元素。 每一次…...
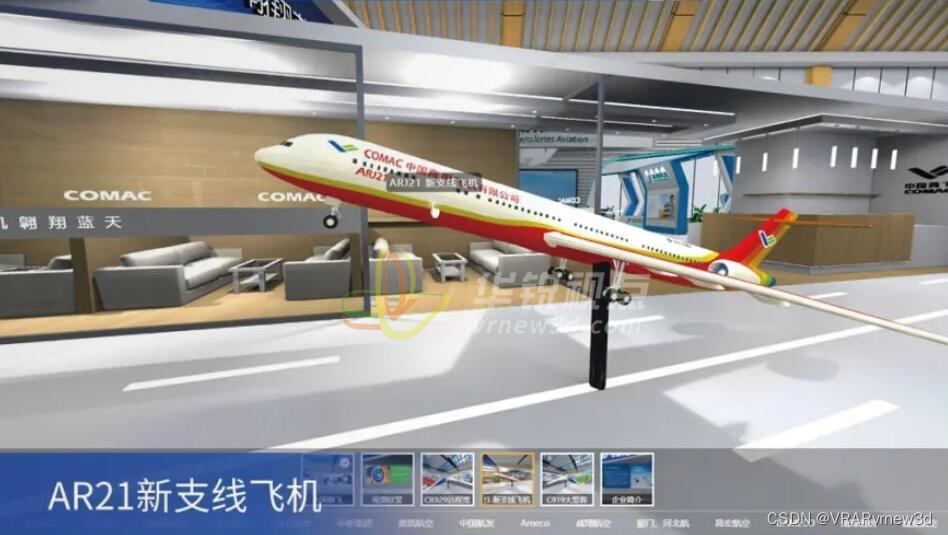
vr飞机驾驶舱模拟流程3D仿真演示加大航飞安全法码
众所周知,航空航天飞行是一项耗资大、变量参数很多、非常复杂的系统工程,因此可利用虚拟仿真技术经济、安全及可重复性等特点,进行飞行任务或操作的模拟,以代替某些费时、费力、费钱的真实试验或者真实试验无法开展的场合…...
一、八大排序(sort)
文章目录 一、时间复杂度(一)定义:常数操作 二、空间复杂度(一)定义: 三、排序(一)选择排序1.定义2.代码3.特性 (二)冒泡排序1.定义2.代码3.特性 (…...
【AWS】AI 代码生成器—Amazon CodeWhisperer初体验 | 开启开挂编程之旅
使用 AI 编码配套应用程序更快、更安全地构建应用程序 文章目录 1.1 Amazon CodeWhisperper简介1.2 Amazon CodeWhisperer 定价2.1 打开VS Code2.2 安装AWS ToolKit插件 一、前言 1.1 Amazon CodeWhisperper简介 1️⃣更快地完成更多工作 CodeWhisperer 经过数十亿行代码的训…...

【Mysql主从配置方法---单主从】
Mysql主从 主服务器 创建用户 create user “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 授权 grant replication slave on . to “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 查看用户权限 SHOW GRANTS FOR “for_rep”“从服务器IP地址”; 修改M…...

⼀⽂读懂加密资产交易赛道的新锐⼒量Bitdu
交易所,仍然是加密资产赛道的皇冠级赛道。围绕这个领域展开的商业竞争,最能引起⼴⼤⽤⼾的关注。 经历了数轮资产价格涨跌的⽜熊之后,⼀批批创业者也在不断地思考这⼀议题 — 如何在去中⼼化的世界中,最⾼效率地集结流量、资本和…...
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】)
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】) 源系统:万里牛 万里牛是杭州湖畔网络技术有限公司旗下SaaS软件品牌,主要针对电商、外贸、实体门店等业务群体,帮助企业快速布局新零售,提升订单处理效…...
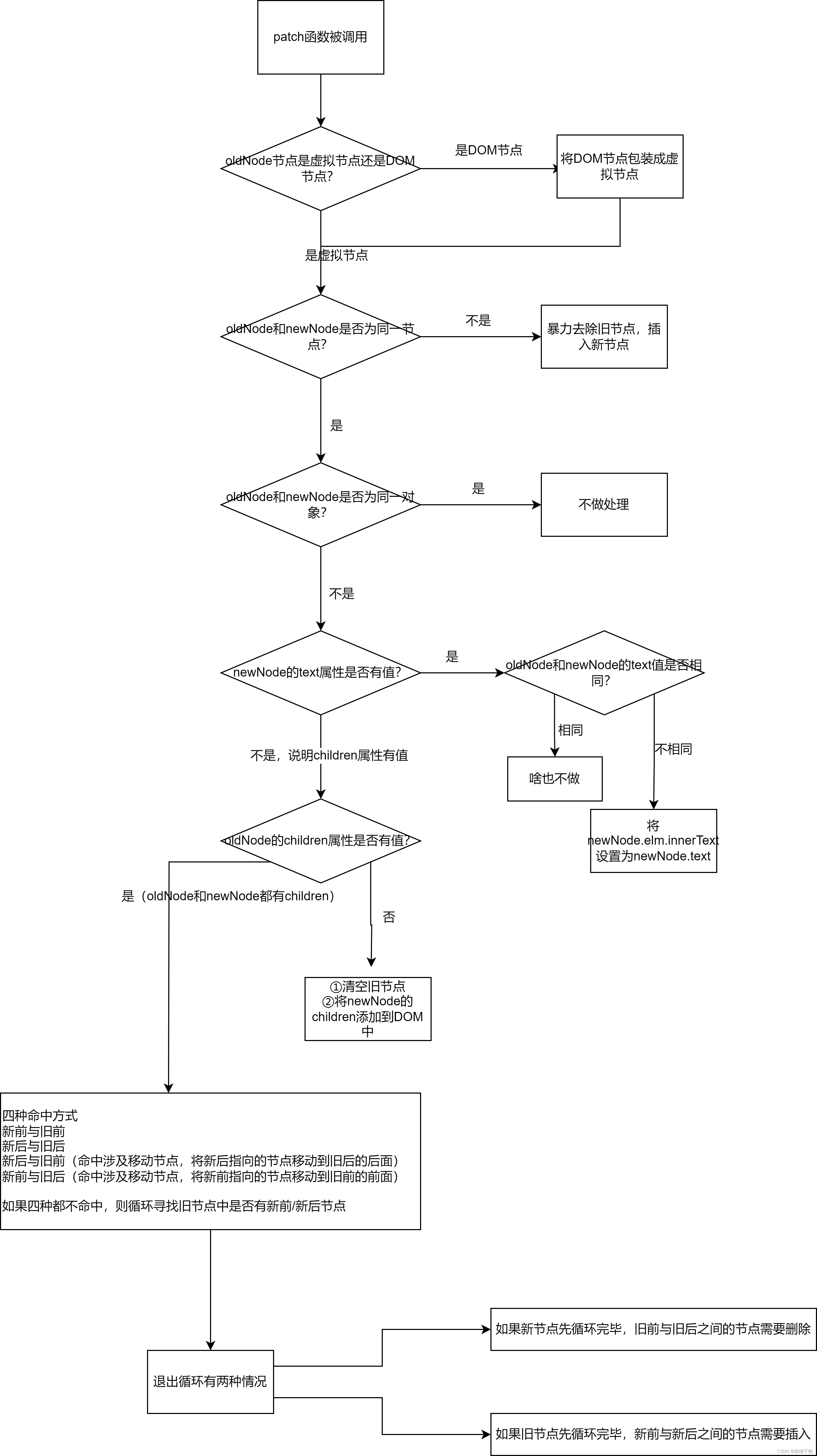
虚拟DOM与diff算法
虚拟DOM与diff算法 snabbdom虚拟DOMdiff算法 snabbdom 是什么:snabbdom是著名的虚拟DOM库,是diff算法的鼻祖,Vue源码借鉴了snabbdom 虚拟DOM 是什么:本质上是存在内存里的 JavaScript 对象 作用:用来描述真实DOM的层…...

K8S:pod资源限制及探针
文章目录 一.pod资源限制1.pod资源限制方式2.pod资源限制指定时指定的参数(1)request 资源(2) limit 资源(3)两种资源匹配方式 3.资源限制的示例(1)官网示例(2࿰…...

CSS中的定位
position 的属性与含义 CSS 中的 position 属性用于控制元素在页面中的定位方式,有四个主要的取值,每个取值都会影响元素的布局方式,它们是: static(默认值): 这是所有元素的初始定位方式。在静…...
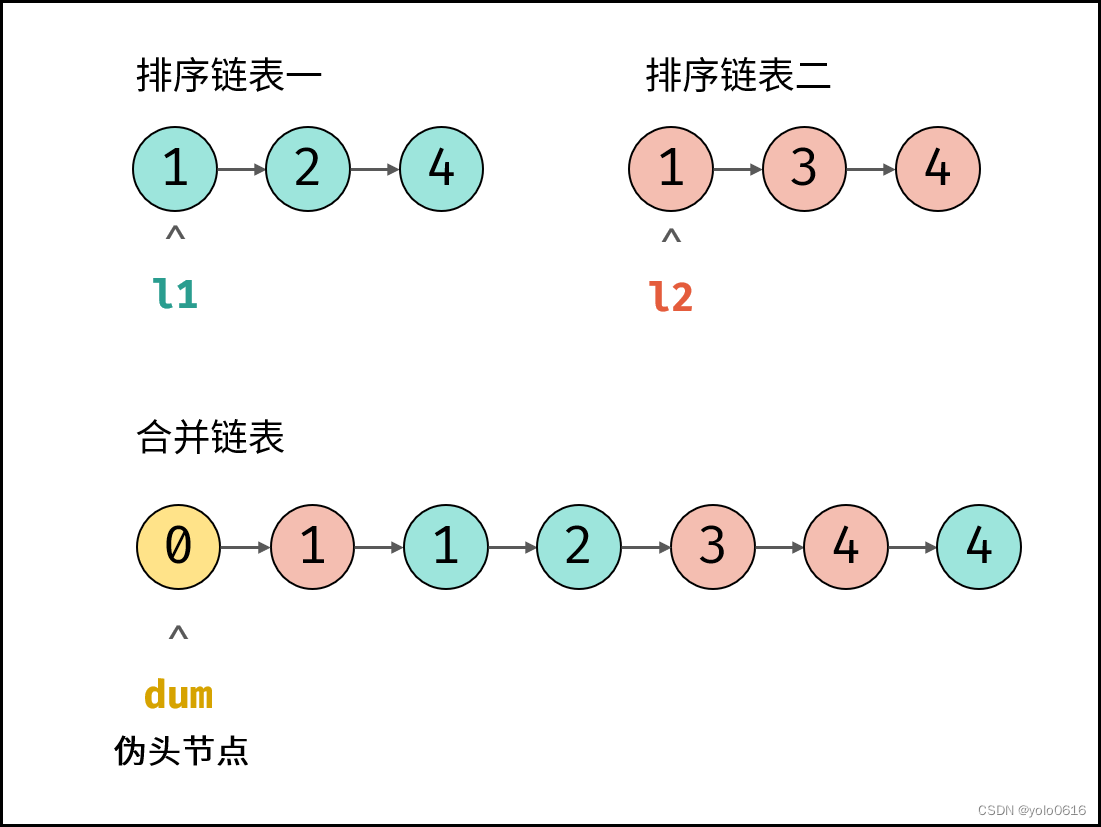
二、链表(linked-list)
文章目录 一、定义二、经典例题(一)[21.合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)1.思路2.复杂度分析3.注意4.代码 (二)[86.分割链表](https://leetcode.cn/problems/partition-list…...
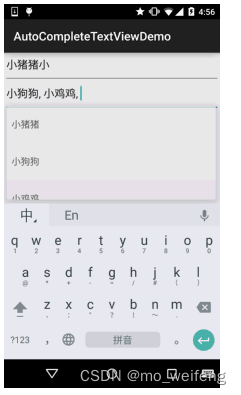
Android EditText筛选+选择功能开发
在日常开发中经常会遇到这种需求,EditText既需要可以筛选,又可以点击选择。这里筛选功能用的是AutoCompleteTextView,选择功能使用的是第三方库https://github.com/kongzue/DialogX。 Android AutoCompleteTextView(自动完成文本框)的基本使用…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
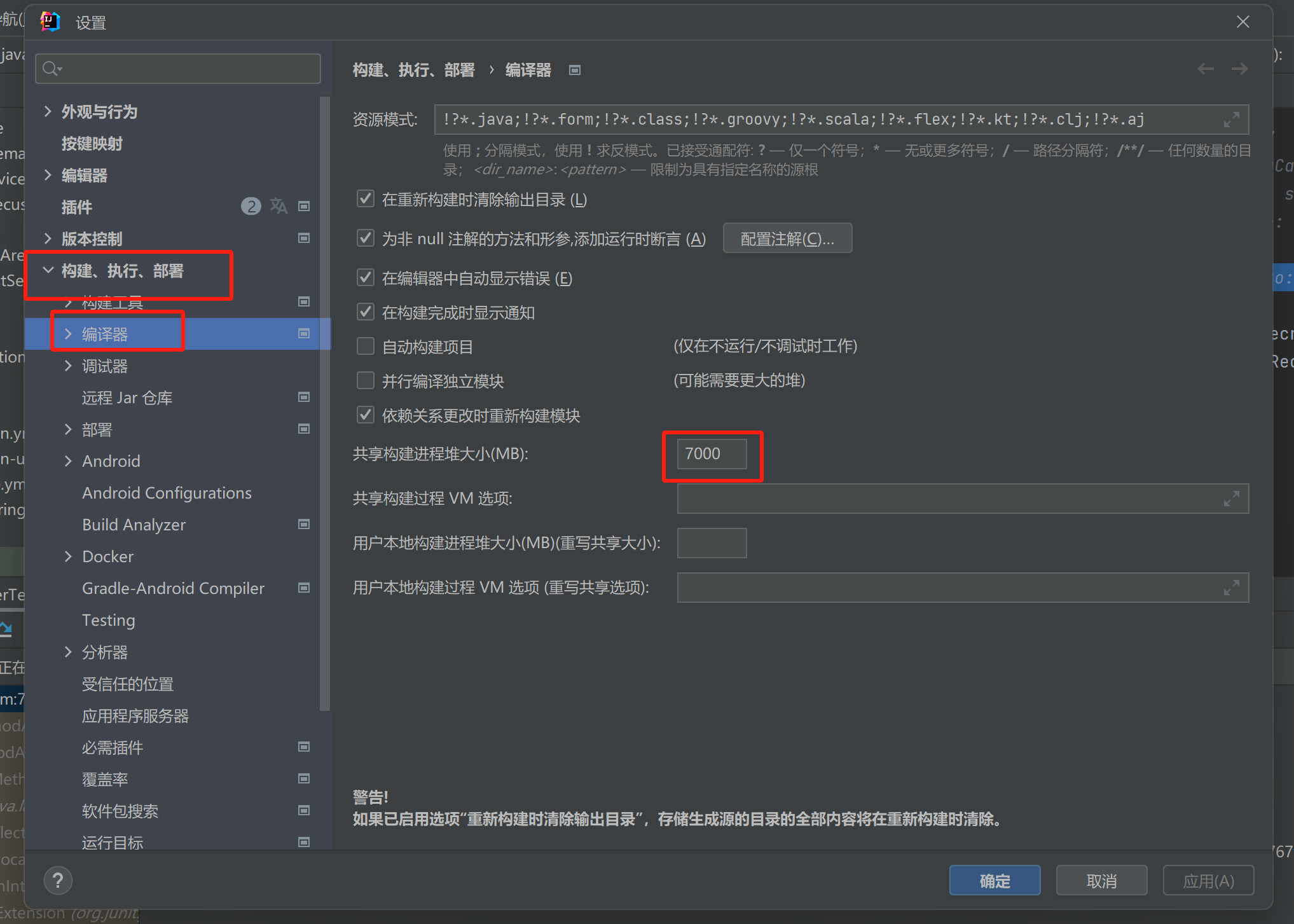
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
