五、回溯(trackback)
文章目录
- 一、算法定义
- 二、经典例题
- (一)排列
- 1.[46.全排列](https://leetcode.cn/problems/permutations/description/)
- (1)思路
- (2)代码
- (3)复杂度分析
- 2.[LCR 083. 全排列](https://leetcode.cn/problems/VvJkup/description/)
- (1)思路
- (2)代码
- (3)复杂度分析
- (二)组合
- (三)子集
- (四)N皇后问题、岛屿问题
- 1.[51.N皇后](https://leetcode.cn/problems/n-queens/)
- (1)思路
- (2)代码
- (3)复杂度分析
一、算法定义
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。
站在回溯树的一个节点上,你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。

二、经典例题
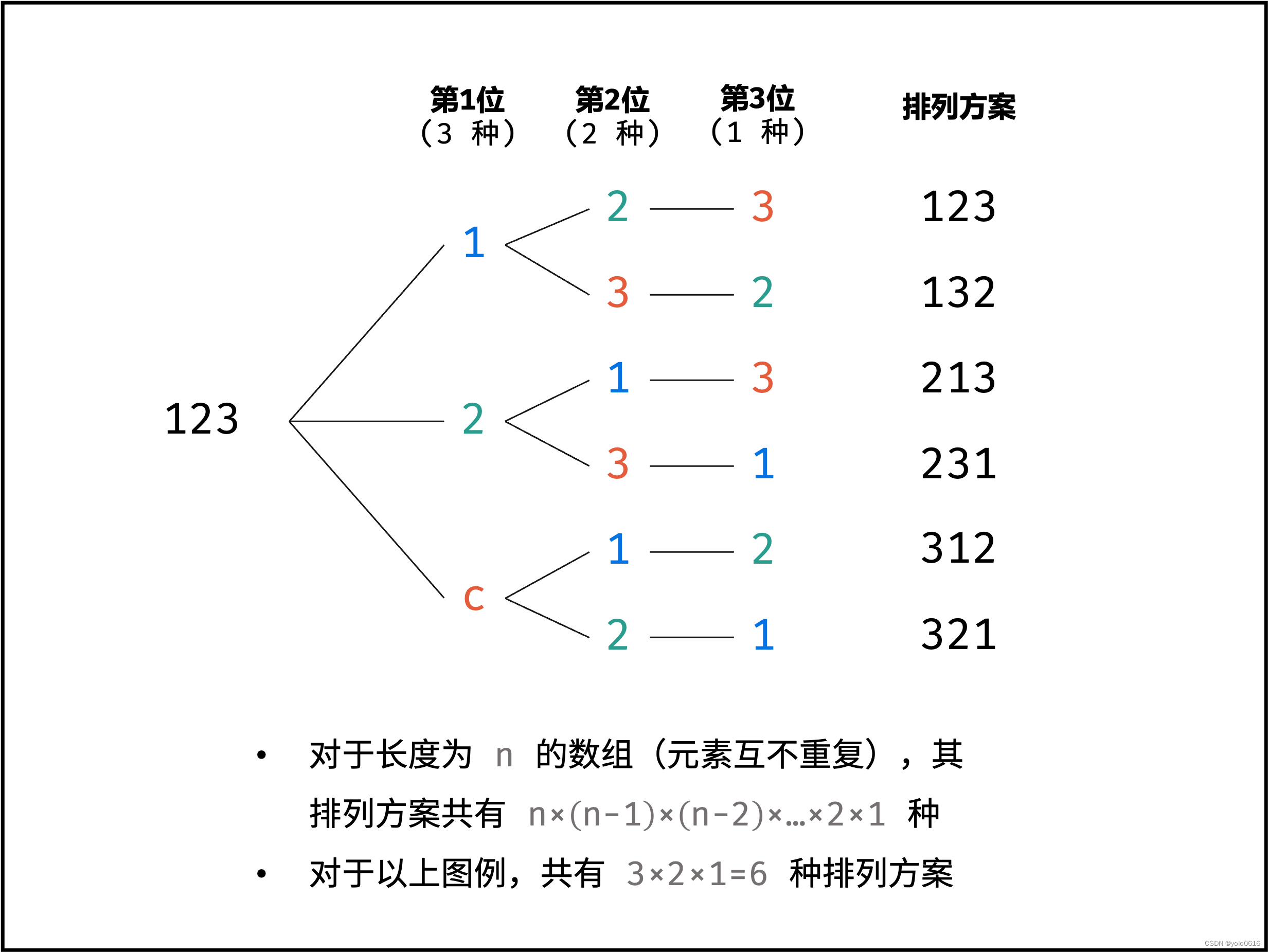
(一)排列
1.46.全排列
(1)思路
(2)代码
class Solution {
public:
vector<vector<int>> res;void dfs(vector<int>& nums) {vector<int> path;vector<bool> used(nums.size(),false);trackback(nums,path,used);}void trackback(vector<int>& nums,vector<int>&path,vector<bool>&used) {if (path.size() == nums.size()) {res.push_back(path);return ;}for (int i = 0; i < nums.size(); i ++) {if (used[i] == true) continue;path.push_back(nums[i]);used[i] = true;trackback(nums, path, used);used[i] = false;path.pop_back();}}vector<vector<int>> permute(vector<int>& nums) {if (nums.size() == 0) return res;dfs(nums);return res;}
};
(3)复杂度分析
时间复杂度:O(n x n!)
空间复杂度:O(n),其中n为序列的长度。除答案数组以外,递归函数在递归过程中需要为每一层递归函数分配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,这里可知递归调用深度为 O(n)。
2.LCR 083. 全排列
(1)思路
(2)代码
class Solution {
public:
vector<vector<int>> res;void process(vector<int>& nums) {vector<int> path;vector<bool> used(nums.size(),false);dfs(used,path,nums);}void dfs(vector<bool>& used,vector<int> &path,vector<int>& nums) {if (path.size() == nums.size()){res.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (used[i]) continue;path.push_back(nums[i]);used[i] = true;dfs(used,path,nums);used[i] = false;path.pop_back();}}vector<vector<int>> permute(vector<int>& nums) {if (nums.size() == 0) return res;sort(nums.begin(),nums.end());process(nums);return res;}
};
(3)复杂度分析
时间复杂度:O(n x n!)
空间复杂度:O(n)
(二)组合
(三)子集
(四)N皇后问题、岛屿问题
1.51.N皇后
(1)思路
(2)代码
class Solution {
public:
vector<vector<string>> res;vector<vector<string>> solveNQueens(int n) {vector<string> board (n,string(n,'.'));backtrack(board,0);return res;}void backtrack(vector<string>& board, int row) {if (row == board.size()) {res.push_back(board);return;}int n = board[row].size();for (int col = 0; col < n; col++) {if (!isvaild(board,row,col)) {continue;}board[row][col] = 'Q';backtrack(board, row + 1);// 撤销选择board[row][col] = '.';}}bool isvaild(vector<string>& board, int row, int col) {int n = board.size();for (int i = 0; i <= row; i++) {if (board[i][col] == 'Q')return false;}for (int i = row - 1,j = col + 1; i >= 0 && j < n;i --,j ++) { // 左上if (board[i][j] == 'Q')return false;}for (int i = row - 1, j = col - 1;i >= 0 && j >= 0; i--, j--) { // 右上if (board[i][j] == 'Q')return false;}return true;}
};
(3)复杂度分析
相关文章:

五、回溯(trackback)
文章目录 一、算法定义二、经典例题(一)排列1.[46.全排列](https://leetcode.cn/problems/permutations/description/)(1)思路(2)代码(3)复杂度分析 2.[LCR 083. 全排列](https://le…...

什么是分布式锁?他解决了什么样的问题?
相信对于朋友们来说,锁这个东西已经非常熟悉了,在说分布式锁之前,我们来聊聊单体应用时候的本地锁,这个锁很多小伙伴都会用 ✔本地锁 我们在开发单体应用的时候,为了保证多个线程并发访问公共资源的时候,…...
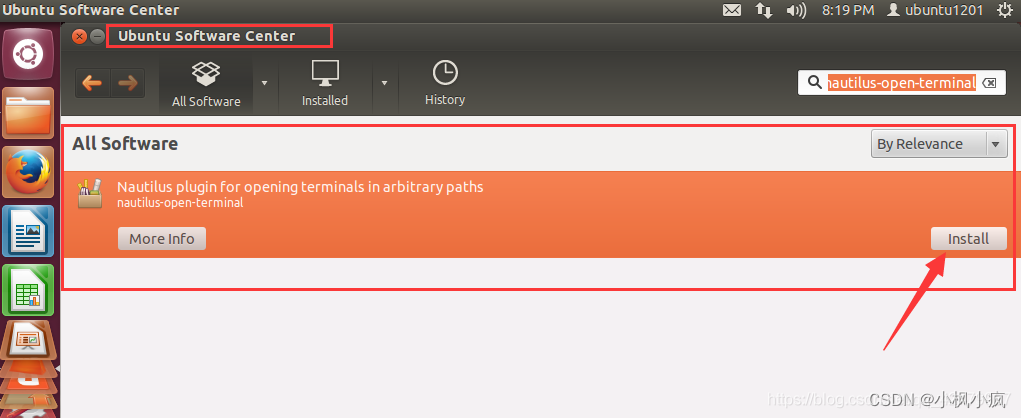
Ubuntu 12.04增加右键命令:在终端中打开增加打开文件
Ubuntu 12.04增加右键命令:在终端中打开 软件中心:搜索nautilus-open-terminal安装 用快捷键CtrlT打开命令行输入: sudo apt-get install nautilus-open-terminal 重新加载文件管理器 nautilus -q 或注销再登录即要使用...

Centos 7 访问局域网windows共享文件夹
Refer: centos7 访问windows系统的共享文件夹_centos访问windows共享_三希的博客-CSDN博客 一、在CentOS中配置CIFS网络存储服务 CIFS(Common Internet File System)是一种在网络上共享文件的协议,也称为SMB(Server Message Blo…...

GDB的TUI模式(文本界面)
2023年9月22日,周五晚上 今晚在看GDB的官方文档时,发现GDB居然有文本界面模式 TUI (Debugging with GDB) (sourceware.org) GDB开启TUI的条件 GDB的文本界面的开启条件是:操作系统有适当版本的curses库 The TUI mode is supported only on…...

深入了解Python和OpenCV:图像的卡通风格化
前言 当今数字时代,图像处理和美化已经变得非常普遍。从社交媒体到个人博客,人们都渴望分享独特且引人注目的图片。本文将介绍如何使用Python编程语言和OpenCV库创建令人印象深刻的卡通风格图像。卡通风格的图像具有艺术性和创意,它们可以用…...

【算法挨揍日记】day06——1004. 最大连续1的个数 III、1658. 将 x 减到 0 的最小操作数
1004. 最大连续1的个数 III 1004. 最大连续1的个数 III 题目描述: 给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 解题思路: 首先题目要我们求出的最多翻转k个0后&#x…...
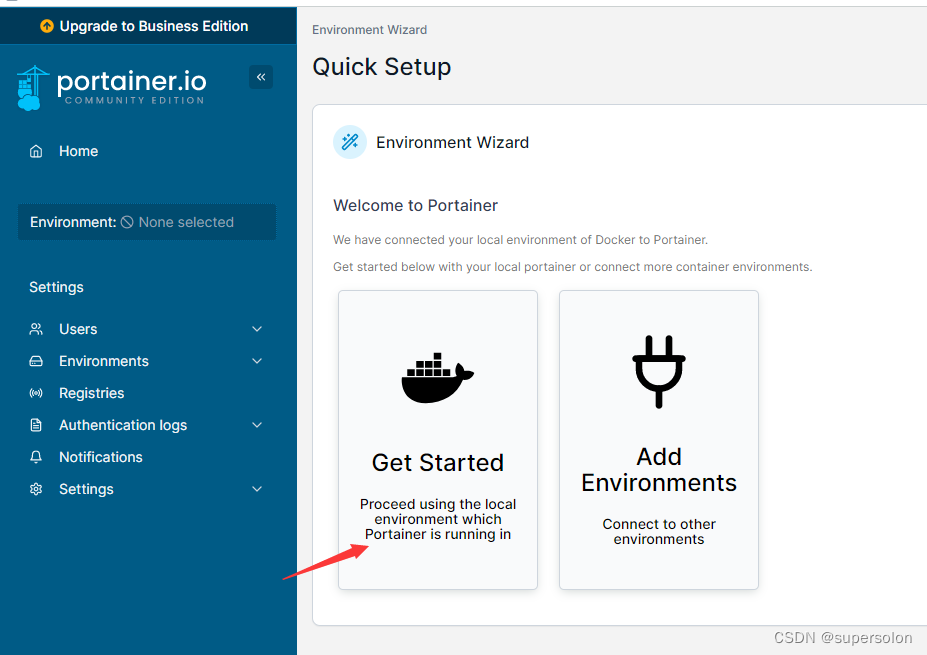
华为云HECS安装docker
1、运行安装指令 yum install docker都选择y,直到安装成功 2、查看是否安装成功 运行版本查看指令,显示docker版本,证明安装成功 docker --version 或者 docker -v 3、启用并运行docker 3.1启用docker 指令 systemctl enable docker …...

力扣669 补9.16
最近大三上四天有早八,真的是受不了了啊,欧嗨呦,早上困如狗,然后,下午困如狗,然后晚上困如狗,尤其我最近在晚上7点到10点这个时间段看力扣,看得我昏昏欲睡,不自觉就睡了1…...

2023-9-22 没有上司的舞会
题目链接:没有上司的舞会 #include <cstring> #include <iostream> #include <algorithm>using namespace std;const int N 6010;int n; int happy[N]; int h[N], e[N], ne[N], idx; bool has_father[N];// 两个状态,选该节点或不选该…...

【HDFS】cachingStrategy的设置
org.apache.hadoop.hdfs.client.impl.BlockReaderFactory#getRemoteBlockReader: private BlockReader getRemoteBlockReader(Peer peer) throws IOException {int networkDistance = clientContext.getNetworkDistance(datanode);return BlockReaderRemote...

性能测试 —— 性能测试常见的测试指标 !
一、什么是性能测试 先看下百度百科对它的定义,性能测试是通过自动化的测试工具模拟多种正常、峰值以及异常负载条件来对系统的各项性能指标进行测试。 我们可以认为性能测试是:通过在测试环境下对系统或构件的性能进行探测,用以验证在生产环…...

【学习草稿】背包问题
一、01背包问题 图解详细解析 (转载) https://blog.csdn.net/qq_37767455/article/details/99086678 :Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个物…...
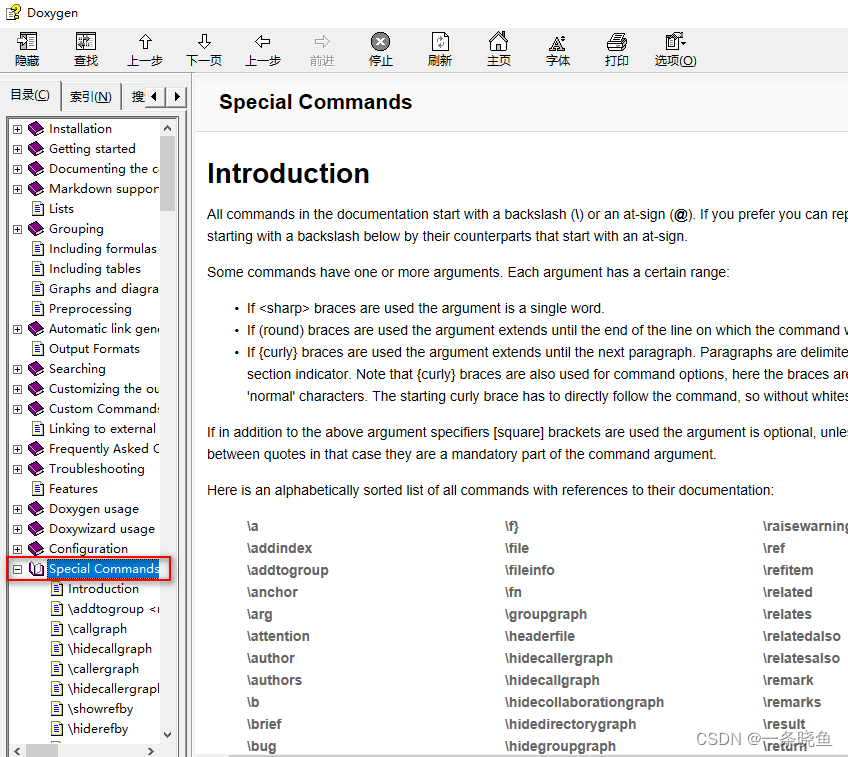
doxygen c++ 语法
c基本语法模板 以 /*! 开头, */ 结尾 /*!\关键字1\关键字2 */1 文件头部信息 /*! \file ClassA.h* \brief 文件说明 定义了类fatherA* \details This class is used to demonstrate a number of section commands.* \author John Doe* \author Jan Doe* \v…...
)
ChatGLM微调基于P-Tuning/LoRA/Full parameter(上)
1. 准备环境 首先必须有7个G的显存以上,torch >= 1.10 需要根据你的cuda版本 1.1 模型下载 $ git lfs install $ git clone https://huggingface.co/THUDM/chatglm-6b1.2 docker环境搭建 环境搭建 $ sudo docker pull slpcat/chatglm-6b:latest $ sudo docker run -it …...

BLE Mesh蓝牙mesh传输大数据包传输文件照片等大数据量通讯
1、BLE Mesh数据传输现状 BLE Mesh网络技术是低功耗蓝牙的一个进阶版,Mesh扩大了蓝牙在应用中的规模和范围,因为它同时支持超过三万个网络节点,可以跨越大型建筑物,不仅可以使得医疗健康应用更加方便快捷,还能监测像学…...
9.18 QT作业
mainwindow.h QT_BEGIN_NAMESPACE namespace Ui { class MainWindow; } QT_END_NAMESPACEclass MainWindow : public QMainWindow {Q_OBJECTpublic:MainWindow(QWidget *parent nullptr);~MainWindow();signals:void jump(); //自定义跳转信号函数private slots:vo…...
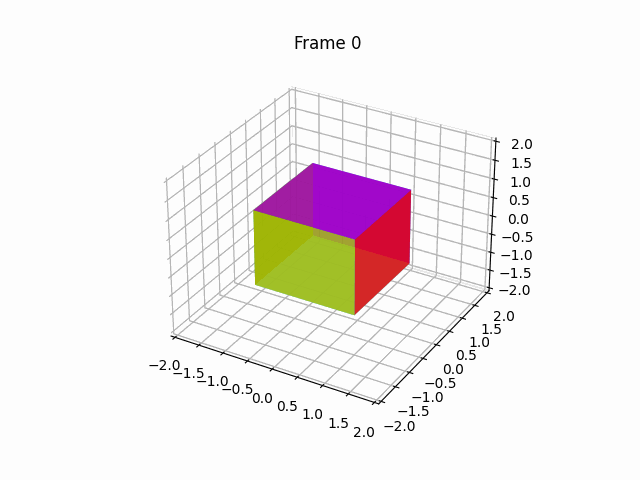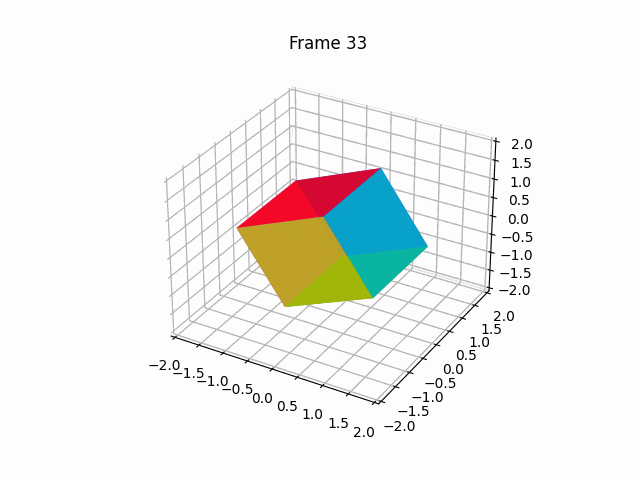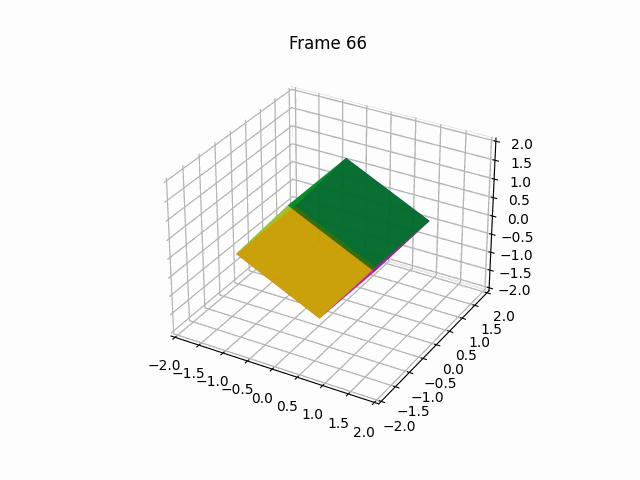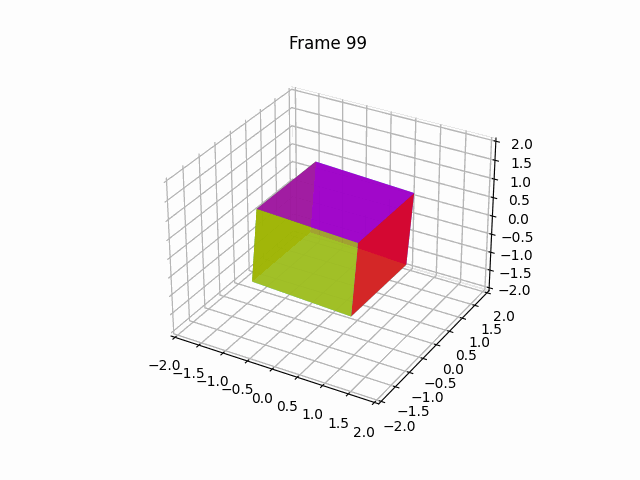
【100天精通Python】Day67:Python可视化_Matplotlib 绘动画,2D、3D 动画 示例+代码
1 绘制2D动画(animation) Matplotlib是一个Python绘图库,它提供了丰富的绘图功能,包括绘制动画。要绘制动画,Matplotlib提供了FuncAnimation类,允许您创建基于函数的动画。下面是一个详细的Matplotlib动画示…...

Linux内核源码分析 (B.x)Linux页表的映射
Linux内核源码分析 (B.x)Linux页表的映射 文章目录 Linux内核源码分析 (B.x)Linux页表的映射一、ARM32页表1、页表术语2、虚拟地址到物理地址转换3、一级页表项4、二级页表项 二、ARM64页表1、ARMv8-A架构2、4KB大小页4级映射 三、Linux内核中关于页表的函数和宏1、查询页表2、…...

机器学习(15)---代价函数、损失函数和目标函数详解
文章目录 一、各自定义二、各自详解三、代价函数和损失函数区别四、例题理解 一、各自定义 1. 代价函数:代价函数(Cost Function)是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。它用于衡量模型在…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
