代码随想录|392.判断子序列,115.不同的子序列(需要二刷)
392.判断子序列
先用双指针做
class Solution {public boolean isSubsequence(String s, String t) {//双指针int m=s.length();int n=t.length();int slow=0;int i=0;int j=0;while(i<m&&j<n){if(s.charAt(i)==t.charAt(j)){i++;System.out.println(i);}j++;}return i==m?true:false;}
}再用动规
1.确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。注意要判断s是否为t的子序列。即t的长度是大于等于s的
2.确定递推公式
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
3.dp初始化
dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],dp[0][0]表示两个空字符串相同子序列的长度,dp[i][0]表示下标为i-1的字符串s与空字符串t的相同子序列的长度,所以dp[0][0],dp[i][0]都初始化为0
4.遍历顺序
根据递推公式可知是从前往后的
5.推导dp
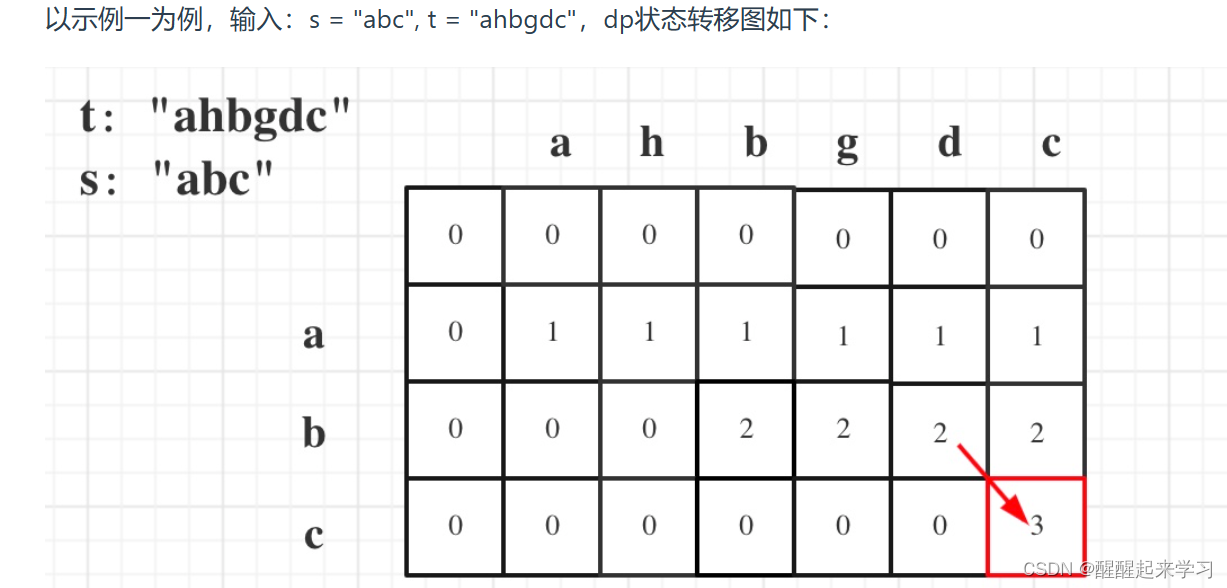
代码实现
class Solution {public boolean isSubsequence(String s, String t) {//动规int m=s.length();int n=t.length();int[][] dp=new int[m+1][n+1];for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(s.charAt(i-1)==t.charAt(j-1)){//比较的是下标i-1和j-1对应的字符dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=dp[i][j-1];}}}return dp[m][n]==m?true:false;}
}115.不同的子序列(需要二刷)
这里要明确,我们要求的是s中有多少个t
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
2.确定递推公式
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
当s[i-1]与t[j-1]不相等时,s中只要一部分能组成t,不用s[i-1]来匹配(就是模拟在s中删除这个元素即:dp[i-1][j])所以递推公式:dp[i][j]=dp[i-1][j]
3.dp初始化
从递推公式dp[i][j]=dp[i-1][j]和dp[i][j]=dp[i-1][j-1]+dp[i-1][j]来看,dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。,dp[i][0]表示以i-1为结尾的字符串s中能匹配出多少个空字符串t,所以dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1;dp[0][j]表示空字符串s能匹配出以j-1为结尾的字符串t的个数,所以dp[0][j]一定都是0,s如论如何也变成不了t。
4.遍历顺序从前往后
5.推导dp
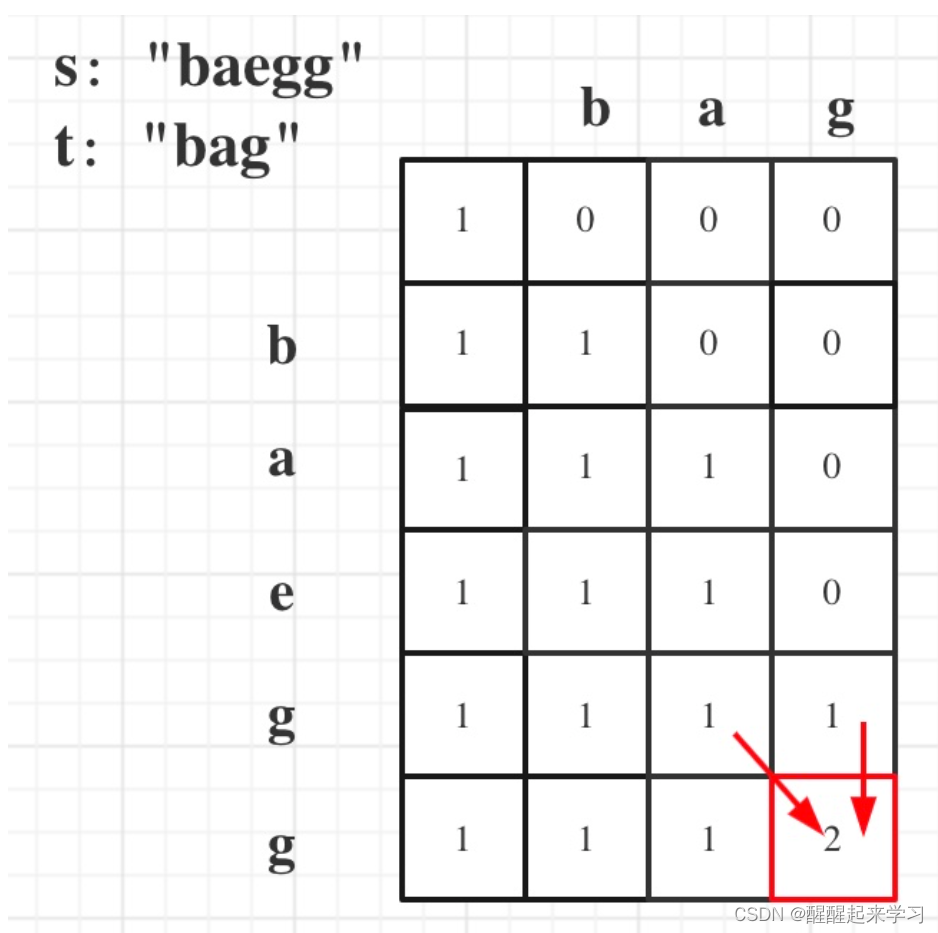
代码实现
class Solution {public int numDistinct(String s, String t) {int m=s.length();int n=t.length();int[][] dp=new int[m+1][n+1];//初始化for(int i=0;i<=m;i++){dp[i][0]=1;}// for (int j = 1; j < t.size(); j++) dp[0][j] = 0; //默认就是初始化为0//递推for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){if(s.charAt(i-1)==t.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+dp[i-1][j]; //如s=bagg,t=bag}else{dp[i][j]=dp[i-1][j];//}}}return dp[m][n];}
}相关文章:

代码随想录|392.判断子序列,115.不同的子序列(需要二刷)
392.判断子序列 先用双指针做 class Solution {public boolean isSubsequence(String s, String t) {//双指针int ms.length();int nt.length();int slow0;int i0;int j0;while(i<m&&j<n){if(s.charAt(i)t.charAt(j)){i;System.out.println(i);}j;}return im?…...
Linux——文件系统
✅<1>主页::我的代码爱吃辣 📃<2>知识讲解:Linux——文件系统 ☂️<3>开发环境:Centos7 💬<4>前言:上期我们了解了文件在内存中得组织方式,那么文件在磁盘中…...

《动手学深度学习 Pytorch版》 7.3 网络中的网络(NiN)
LeNet、AlexNet和VGG的设计模式都是先用卷积层与汇聚层提取特征,然后用全连接层对特征进行处理。 AlexNet和VGG对LeNet的改进主要在于扩大和加深这两个模块。网络中的网络(NiN)则是在每个像素的通道上分别使用多层感知机。 import torch fr…...

古代有没有电子元器件?
手机,电脑,电视等等电子产品,无时无刻充斥在我们的生活中,如果有一天突然没有了这些功能多样的电子产品,估计大部分人都会一时之间难以适应。 这就好比正在上网,结果突然被人断了网,导致无网络连…...

log4j2或者logback配置模版实现灵活输出服务名
介绍 在我们使用log4j2或者logback打印日志时,输出的内容中通常是一定要加上服务名的。以log4j2为例: <!--输出控制台的配置--> <Console name"Console" target"SYSTEM_OUT"><!-- 输出日志的格式 --><Patter…...

使用HTTP爬虫ip中的常见误区与解决方法
在如今的互联网时代,为了保障个人隐私和实现匿名浏览,许多人选择使用HTTP爬虫ip。然而,由于缺乏了解和使用经验,常常会出现一些误区。本文将为大家介绍使用HTTP爬虫ip过程中常见的误区,并提供相应的解决方法࿰…...
MySQL学习笔记3
MySQL的源码编译安装: 1、参考MySQL的源码安装官方文档: 2、源码安装定制选项: 3、源码安装三部曲:配置、编译、安装。 4、软件安装包: mysql-boost-5.7.43.tar.gz 5、安装需求: 安装需求具体配置安装目…...

快速掌握ES6
什么是ES6 ES6(ECMAScript 6),也被称为ES2015,是JavaScript的第六个版本,于2015年发布。ES6引入了许多新的语法和功能,旨在提高JavaScript的开发效率和代码质量。 ES6的一些主要特性和改进包括࿱…...

电池厂提供excel电池曲线zcv到mtk电池曲线zcv转换
#encoding:utf8 #电池厂提供excel电池曲线zcv到mtk电池曲线zcv转换 import pandas as pd import openpyxl import math # 读取Excel文件 df pd.read_excel("a55-zcv.xlsx") for j in range(0,10): if(j<3): offset0 #T0~T2 if(j3): offset…...

重写和重载、抽象类和接口
文章目录 前言一、重载与重写1.重载(Overload)(1)条件(2)举例 2.重写(Override)(1)规则(2)举例 3.重载和重写区别 二、抽象类与接口1.抽象类&…...

Untiy UDP局域网 异步发送图片
同步画面有问题,传图片吧 using System.Text; using System.Net.Sockets; using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.Events; using System.Net; using System; using System.Threading.Tasks; using Sy…...

移动端H5封装一个 ScrollList 横向滚动列表组件,实现向左滑动
效果: 1.封装组件: <template><div class"scroll-list"><divclass"scroll-list-content":style"{ background, color, fontSize: size }"ref"scrollListContent"><div class"scroll…...

Docker一键安装和基本配置
一键安装脚本 注:该脚本需要root权限 curl -sSL https://get.docker.com/ | sh非root组用户赋权 sudo groupadd docker # 若使用一键安装脚本会自动创建这个组,提示已存在 sudo gpasswd -a ${USER} docker # 将当前用户添加到docker组,也…...

MVC设计思想理解和ASP.NET MVC理解
三层模式 三层模式包括:UI层,业务逻辑层,数据访问层,模型层 MVC设计思想和ASP.NET MVC理解 MVC设计思想: MVC的思想就是把我们的程序分为三个核心的模块,这三个模块的详细介绍如下: 模型(Model) :负责封装与引用程序的业务逻辑相关的数据以及对数据的处理方法。模型层有对…...

大模型应用选择对比
大模型应用选择对比 1、知识库对比:dify、fastgpt、langchatchat 2、agent构建器选择:flowise、langflow、bisheng 3、召回率提升方案...

c++STL概述
目录 STL基本概念 STL六大组件 STL的优点 STL三大组件 容器 算法 迭代器 普通的迭代器访问vector容器元素 算法for_each实现循环 迭代器指向的元素类型是自定义数据类型 迭代器指向容器 常用容器 string容器 string的基本概念 string容器的操作 string的构造函…...

利用容器技术优化DevOps流程
利用容器技术优化DevOps流程 随着云计算的快速发展,容器技术也日益流行。容器技术可以打包和分发应用程序,并实现快速部署和扩展。在DevOps流程中,容器技术可以大大优化开发、测试、部署和运维各个环节。本文将介绍如何利用容器技术优化DevO…...

91 # 实现 express 的优化处理
上一节实现 express 的请求处理,这一节来进行实现 express 的优化处理 让 layer 提供 match 方法去匹配 pathname,方便拓展让 layer 提供 handle_request 方法,方便拓展利用第三方库 methods 批量生成方法性能优化问题 进行路由懒加载&#…...
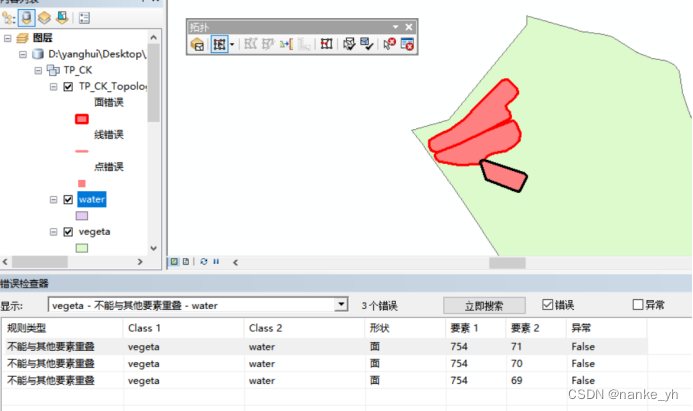
arcgis拓扑检查实现多个矢量数据之间消除重叠区域
目录 环境介绍: 操作任务: 步骤: 1、数据库和文件结构准备 2、建立拓扑规则 3、一直下一页默认参数后,进行拓扑检查 4、打开TP_CK_Topology,会自动带出拓扑要素,红色区域为拓扑错误的地方࿱…...

基于Vue+ELement搭建登陆注册页面实现后端交互
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《ELement》。🎯🎯 …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
