数据结构————寻路算法
(一)基础补充
二维数组
定义:基本概念与方法和一维数组相似,一般形式为:类型符 数组名[常量表达式][常量表达式];
其中,数组长度只能是常量;通常把二维数组第一个下标理解成行,第二个下标为列,常量表达式: 表达式里面只有常量的式子(如数字类常量);
二维数组常用于描述二维空间,因而可以使用二维数组来描述地图,如1:表示墙,0 表示空地,……我们可以利用二维数组的性质,构建一个简单的二维空间。如
//0:空地 1:墙 3:目的地 4:箱子 5:人 8:人站在目的地 7:箱在目的地
int map[8][8] = {
0,0,1,1,1,0,0,0,
0,0,1,3,1,0,0,0,
0,0,1,0,1,0,0,0,
1,1,1,4,0,1,1,0,
1,3,0,4,5,4,3,1,
1,1,1,1,4,1,1,0,
0,0,1,1,3,1,0,0,
0,0,0,1,1,1,0,0,
};
//打印地图
void show()
{
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 8; j++) {
switch (map[i][j])
{
case 0:
printf(" ");
break;
case 1相关文章:

数据结构————寻路算法
(一)基础补充 二维数组 定义:基本概念与方法和一维数组相似,一般形式为:类型符 数组名[常量表达式][常量表达式]; 其中,数组长度只能是常量;通常把二维数组第一个下标理解成行,第二个下标为列,常量表达式: 表达式里面只有常量的式子(如数字类常量); 二维数组常…...

蓝桥杯 题库 简单 每日十题 day7
01 啤酒和饮料 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。啤酒每罐2.3元,饮料每罐1.9元。小明买了若干啤酒和饮料,一共花了82.3元。我们还知道他买的啤酒比饮料的数量少,请你…...

go -- 获取当前24点的时间戳 --chatGpt
gpt: 要获取当前24点的时间戳,你可以使用 Go 标准库中的 time 包来实现。以下是一个示例函数,它可以获取当前日期的24点的时间戳: go package main import ( "fmt" "time" ) func getMidnightTimestamp() in…...

docker 容器内手动设置服务自启动
需求描述:不使用DockerFile实现容器内的服务自动启动 1、创建执行程序,以crond为例 //进入容器xxx docker exec -it xxx /bin/sh //切换root账户 bash //创建自动执行文件 vim /root/cron.sh2、自动执行文件内容 crond start3、修改执行文件权限 chmod x /root/…...
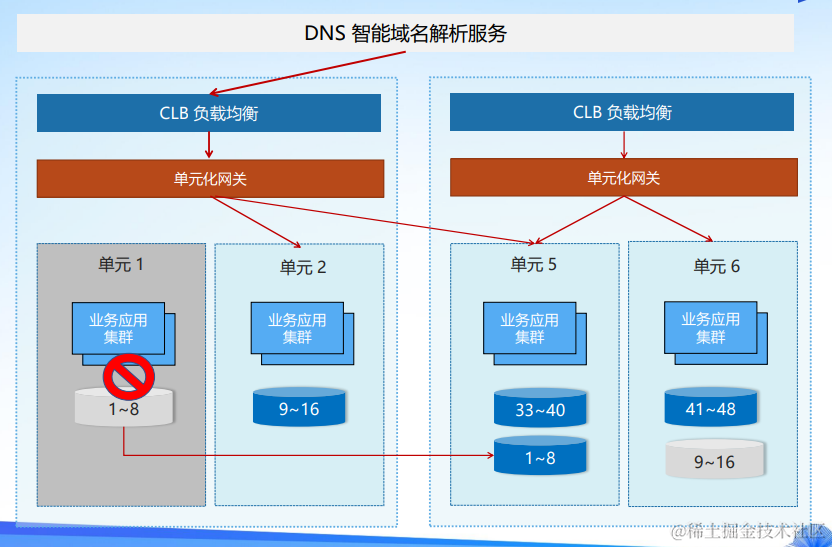
腾讯云微服务平台 TSF 异地多活单元化能力重磅升级
导语 2023腾讯全球数字生态大会已于9月7-8日完美落幕,40专场活动展示了腾讯最新的前沿技术、核心产品、解决方案。 微服务与消息队列专场,腾讯云微服务平台 TSF 产品经理张桢带来了《腾讯云微服务平台 TSF 异地多活单元化能力重磅升级》的精彩演讲。本…...

01贪心:算法理论知识
贪心:01算法理论知识 什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 这么说有点抽象,来举一个例子: 例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额࿰…...
目标分类笔记(二): 利用PaddleClas的框架来完成多标签分类任务(从数据准备到训练测试部署的完整流程)
文章目录 一、演示多分类效果二、PaddleClas介绍三、代码获取四、数据集获取五、环境搭建六、数据格式分析七、模型训练7.1 模型恢复训练7.2 多卡训练7.3 其他训练指标 八、模型预测九、模型评估十、PaddleClas相关博客 一、演示多分类效果 二、PaddleClas介绍 PaddleClas主要…...

PageHelp插件在复杂sql下引起的Having无法识别错误及其解决方案
1: 问题出现的场景 系统中有一个复杂SQL内嵌套了多个子查询.在改动时需要将SQL的最后一行加上having来做额外的过滤处理. 添加完having语句后发现SQL能够正常执行就直接将代码提交到了测试环境.结果在测试环境报错Unknown column ‘xxx‘ in ‘having clause. 2: 分析问题 1…...
linux中的开发工具
在刚开始使用linux的时候,我们需要在系统上写一些简单的代码,来熟悉环境以及各种指令 并且熟悉属于linux的一套开发的环境,而这对于c来说需要三个软件就可以进行简单的编码 和使用,让我们来认识一下下列工具,以及工具的…...

2023 第十二届中国智能产业高峰论坛 - 文档大模型的未来展望
目录 前言文档图像分析识别与理解中的技术挑战 文档图像分析识别与理解的研究主题文档图像分析与预处理文档解析与识别版面分析与还原文档信息抽取与理解AI安全知识化&存储检索和管理 多模态大模型在文档图像处理中的应用多模态的GPT-4在文档图像上的表现多模态的Google Ba…...

【小沐学NLP】关联规则分析Apriori算法(Mlxtend库,Python)
文章目录 1、简介2、Mlxtend库2.1 安装2.2 功能2.2.1 User Guide2.2.2 User Guide - data2.2.3 User Guide - frequent_patterns 2.3 入门示例 3、Apriori算法3.1 基本概念3.2 apriori3.2.1 示例 1 -- 生成频繁项集3.2.2 示例 2 -- 选择和筛选结果3.2.3 示例 3 -- 使用稀疏表示…...

对话ChatGPT:AIGC时代下,分布式存储的应用与前景
随着科技的飞速发展,我们正步入一个被称为AIGC时代的全新阶段,人工智能、物联网、大数据、云计算成为这个信息爆炸时代的主要特征。自2022年11月以来,ChatGPT的知名度迅速攀升,引发了全球科技爱好者的极大关注,其高超的…...

java多线程学习笔记一
一、线程的概述 1.1 线程的相关概念 1.1.1 进程(Process) 进程(Process)是计算机的程序关于某数据集合上的一次运行活动,是操作系统进行资源分配与调度的基本单位。 可以把进程简单的理解为操作系统中正在有运行的一…...

BOM与DOM--记录
BOM基础(BOM简介、常见事件、定时器、this指向) BOM和DOM的区别和联系 JavaScript的DOM与BOM的区别与用法详解 DOM和BOM是什么?有什么作用? 图解BOM与DOM的区别与联系 BOM和DOM详解 JavaScript 中的 BOM(浏览器对…...
Docker安装MongoDB
一、docker安装mongodb MongoDB 是一个免费的开源跨平台面向文档的 NoSQL 数据库程序。 二、安装步骤 1.docker 拉取mysql镜像 docker pull mongo:latest 2.运行容器 docker run -itd --name mongo -p 27017:27017 mongo --auth参数说明: -p 27017:27017 &#…...

不要对正则表达式进行频繁重复预编译
背景 在频繁调用场景,如方法体内或者循环语句中,新定义Pattern会导致重复预编译正则表达式,降低程序执行效率。另外,在 JDK 中部分 入参为正则表达式格式的 API,如 String.replaceAll, String.split 等,也…...

vue入门及小项目小便签条
vue 框架:是一个半成品软件,是一套可重用的,通用的,软件基础代码模型。基于框架进行开发,更加快捷 ,更加高效 v-bind为HTML标签绑定属性值,如设置href,css样式等 v-model在表单元素上创建双向数…...

详解TCP/IP协议第四篇:数据在网络中传输方式的分类概述
文章目录 前言 一:面向有连接型与面向无连接型 1:大致概念 2:面向有连接型 3:面向无连接型 二:电路交换与分组交换 1:分组交换概念 2:分组交交换过程 三:根据接收端数量分…...

SpringMvc决战-【SpringMVC之自定义注解】
目录 一、前言 1.1.什么是注解 1.2.注解的用处 1.3.注解的原理 二.注解父类 1.注解包括那些 2.JDK基本注解 3. JDK元注解 4.自定义注解 5.如何使用自定义注解(包括:注解标记【没有任何东西】,元数据注解)? 三…...
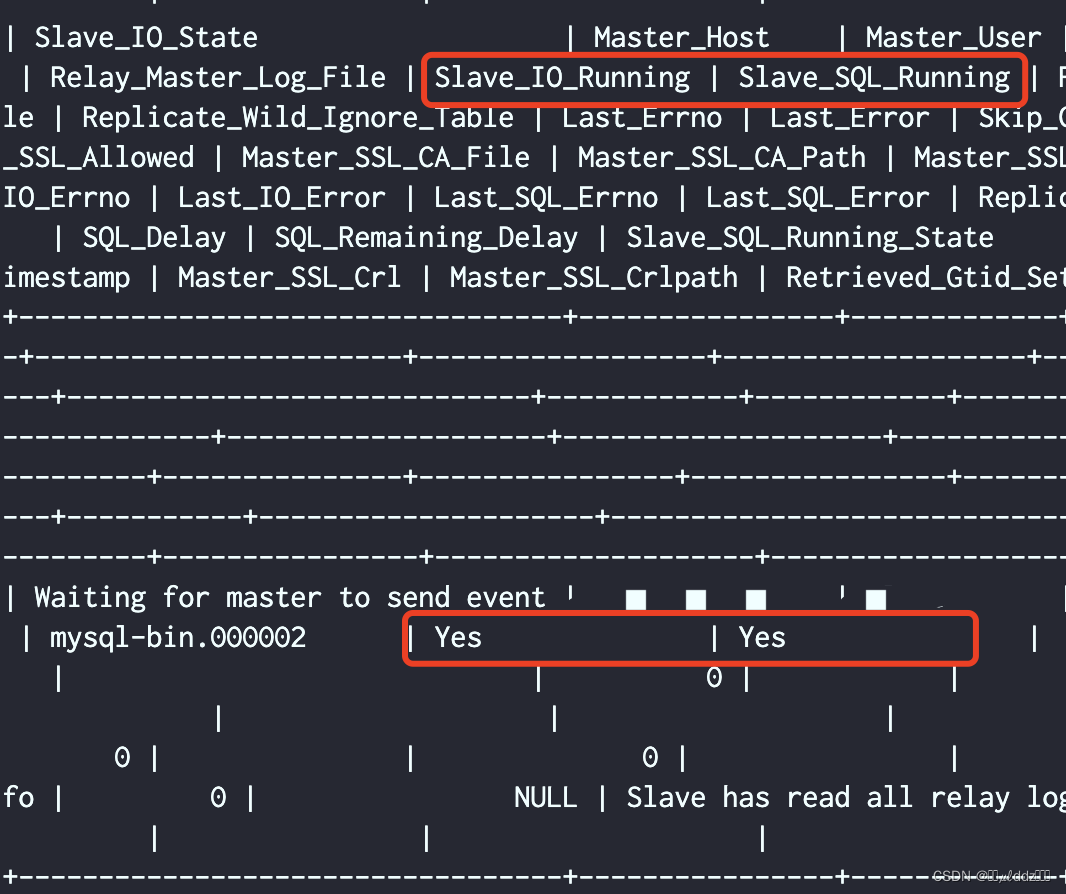
【MySQL集群一】CentOS 7上搭建MySQL集群:一主一从、多主多从
CentOS 7上搭建MySQL集群 介绍一主一从步骤1:准备工作步骤2:安装MySQL步骤3:配置主服务器步骤4:创建复制用户步骤5:备份主服务器数据,如果没有数据则省略这一步步骤6:配置从服务器步骤7…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
