【1993. 树上的操作】
来源:力扣(LeetCode)
描述:
给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点,所以 parent[0] = -1 ,因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁,解锁和升级操作。
数据结构需要支持如下函数:
- Lock: 指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。
- Unlock: 指定用户给指定节点 解锁 ,只有当指定节点当前正被指定用户锁住时,才能执行该解锁操作。
- Upgrade: 指定用户给指定节点 上锁 ,并且将该节点的所有子孙节点 解锁 。只有如下 3 个条件 全部 满足时才能执行升级操作:
- 指定节点当前状态为未上锁。
- 指定节点至少有一个上锁状态的子孙节点(可以是 任意 用户上锁的)。
- 指定节点没有任何上锁的祖先节点。
请你实现 LockingTree 类:
- LockingTree(int[] parent) 用父节点数组初始化数据结构。
- lock(int num, int user) 如果 id 为 user 的用户可以给节点 num 上锁,那么返回 true ,否则返回 false 。如果可以执行此操作,节点 num 会被 id 为 user 的用户 上锁 。
- unlock(int num, int user) 如果 id 为 user 的用户可以给节点 num 解锁,那么返回 true ,否则返回 false 。如果可以执行此操作,节点 num 变为 未上锁 状态。
- upgrade(int num, int user) 如果 id 为 user 的用户可以给节点 num 升级,那么返回 true ,否则返回 false 。如果可以执行此操作,节点 num 会被 升级 。
示例 1:

输入:
["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
输出:
[null, true, false, true, true, true, false]解释:
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2); // 返回 true ,因为节点 2 未上锁。// 节点 2 被用户 2 上锁。
lockingTree.unlock(2, 3); // 返回 false ,因为用户 3 无法解锁被用户 2 上锁的节点。
lockingTree.unlock(2, 2); // 返回 true ,因为节点 2 之前被用户 2 上锁。// 节点 2 现在变为未上锁状态。
lockingTree.lock(4, 5); // 返回 true ,因为节点 4 未上锁。// 节点 4 被用户 5 上锁。
lockingTree.upgrade(0, 1); // 返回 true ,因为节点 0 未上锁且至少有一个被上锁的子孙节点(节点 4)。// 节点 0 被用户 1 上锁,节点 4 变为未上锁。
lockingTree.lock(0, 1); // 返回 false ,因为节点 0 已经被上锁了。
提示:
- n == parent.length
- 2 <= n <= 2000
- 对于 i != 0 ,满足 0 <= parent[i] <= n - 1
- parent[0] == -1
- 0 <= num <= n - 1
- 1 <= user <= 104
- parent 表示一棵合法的树。
- lock ,unlock 和 upgrade 的调用 总共 不超过 2000 次。
方法:深度优先搜索
思路
按照题目要求,依次实现各个函数即可:
- Lock:可以用一个数组变量 lockNodeUser 记录给各个节点上锁的用户,lockNodeUser[num] 即表示给节点 num 上锁的用户。当lockNodeUser[num] = −1 时,即表示 节点 num 未被上锁,通过给 lockNodeUser[num] 赋值实现上锁。
- Unlock:通过比较变量 lockNodeUser[num] 和 user 是否先等来判断当前节点是否可以解锁,通过赋值来解锁。
- Upgrade:实现较为复杂,首先需要判断三个条件是否同时成立,如果是,还需要给指定节点上锁并且给它的所有子孙节点解锁。三个条件中:
- 指定节点当前状态为未上锁:通过变量 lockNodeUser 来判断。
- 指定节点没有任何上锁的祖先节点:需要依次遍历当前节点的父亲节点,通过变量 lockNodeUser 和 parent 来判断。具体代码中,我们利用一个函数 hasLockedAncestor 来实现这一判断。
- 指定节点至少有一个上锁状态的子孙节点:我们将这一判断放到第三步来进行,使得它可以和「给它的所有子孙节点解锁」同时实现。三个状态的判断,我们用「短路与」来连接,当只有前两步都为真,才会进行第三步。当第三步也为真,那么我们就需要进行「给它的所有子孙节点解锁」这一步;当第三步为假,就说明指定节点没有上锁的子孙节点,那么我们仍可以进行「给它的所有子孙节点解锁」这一步,并不影响树的状态。我们定义一个递归函数 checkAndUnlockDescendant 来实现这一步,返回一个布尔值表示当前节点是否有上锁的子孙节点(也包括自己),同时将所有的子孙节点(也包括自己)解锁。遍历子孙节点时,我们提前构建一个变量 children,表示当前节点的孩子节点,这一步可以在初始化时完成。
最后,如果这三个条件与的结果为真,将当前节点上锁。
代码:
class LockingTree {
public:LockingTree(vector<int>& parent) {int n = parent.size();this->parent = parent;this->lockNodeUser = vector<int>(n, -1);this->children = vector<vector<int>>(n);for (int i = 0; i < n; i++) {int p = parent[i];if (p != -1) {children[p].emplace_back(i);}}}bool lock(int num, int user) {if (lockNodeUser[num] == -1) {lockNodeUser[num] = user;return true;} return false;}bool unlock(int num, int user) {if (lockNodeUser[num] == user) {lockNodeUser[num] = -1;return true;}return false;}bool upgrade(int num, int user) {bool res = lockNodeUser[num] == -1 \&& !hasLockedAncestor(num) \&& checkAndUnlockDescendant(num);if (res) {lockNodeUser[num] = user;}return res;}bool hasLockedAncestor(int num) {num = parent[num];while (num != -1) {if (lockNodeUser[num] != -1) {return true;}num = parent[num];}return false;}bool checkAndUnlockDescendant(int num) {bool res = lockNodeUser[num] != -1;lockNodeUser[num] = -1;for (int child : children[num]) {res |= checkAndUnlockDescendant(child);} return res;}private:vector<int> parent;vector<int> lockNodeUser;vector<vector<int>> children;
};
时间 328ms 击败 62.96%使用 C++ 的用户
内存 117.67MB 击败 94.44%使用 C++ 的用户
复杂度分析
- 时间复杂度:初始化:构建 children 消耗 O(n),Lock 和 Unlock 都消耗 O(1),Upgrade 消耗 O(n)。
- 空间复杂度:初始化消耗 O(n),Lock 和 Unlock 都消耗 O(1),Upgrade 消耗 O(n)。
author:力扣官方题解
相关文章:

【1993. 树上的操作】
来源:力扣(LeetCode) 描述: 给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点,所以 par…...

LeetCode【1. 两数之和】
穷通有命无须卜,富贵何时乃济贫;角逐名场今已久,依然一幅旧儒巾。 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输…...
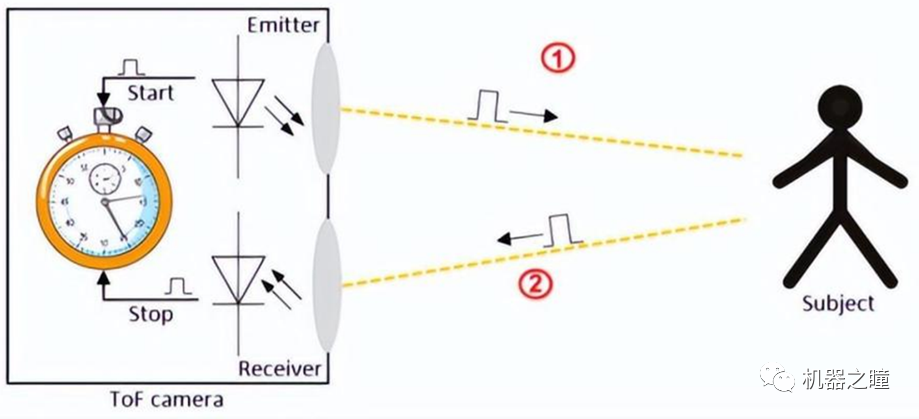
3D成像技术概述
工业4.0时代,三维机器视觉备受关注,目前,三维机器视觉成像方法主要分为光学成像法和非光学成像法,这之中,光学成像法是市场主流。 飞行时间3D成像 飞行时间成像(Time of Flight),简称TOF,是通过给目标连续发送光脉冲,然后用传感器接收从物体返回的光,通过探测光脉…...
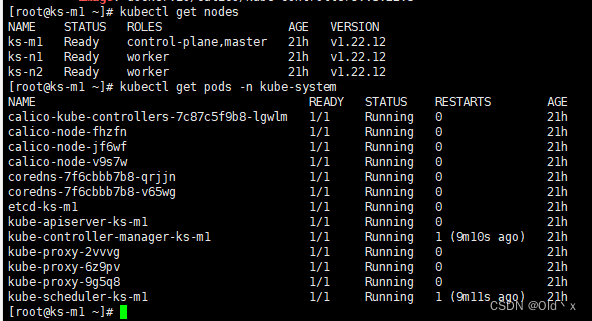
Centos7 安装部署 Kubernetes(k8s) 高可用集群
1:基础环境准备 宿主机系统集群角色服务器IP主机名称容器centos7.6master192.168.2.150ks-m1dockercentos7.6master192.168.2.151ks-n1dockercentos7.6master192.168.2.152ks-n2docker 1.1 服务器初始化及网络配置 VMware安装Centos7并初始化网络使外部可以访问*…...

c++加速方法大全
我们平常写代码的时候,经常超时,非常难受,所以,我写了这篇文章,让你的代码提升速度(这些方法作者亲测有效,用了这些方法,足足提升了1秒!虽然最后题目还是没过)…...

【国科大卜算】Truck History 最小生成树Prim
Truck History 文章目录 Truck Historyproblem descriptionInputOutputSample个人理解 problem description Advanced Cargo Movement, Ltd. uses trucks of different types. Some trucks are used for vegetable delivery, other for furniture, or for bricks. The company…...

SQLAlchemy映射表结构和对数据的CRUD
目录 ORM模型映射到数据库中 SQLAlchemy对数据的增删改查操作编辑 构建session对象 添加对象 查找对象 修改对象 删除对象 ORM模型映射到数据库中 用declarative_base根据engine创建一个ORM基类 from sqlalchemy.ext.declarative import declarative_base engine cr…...
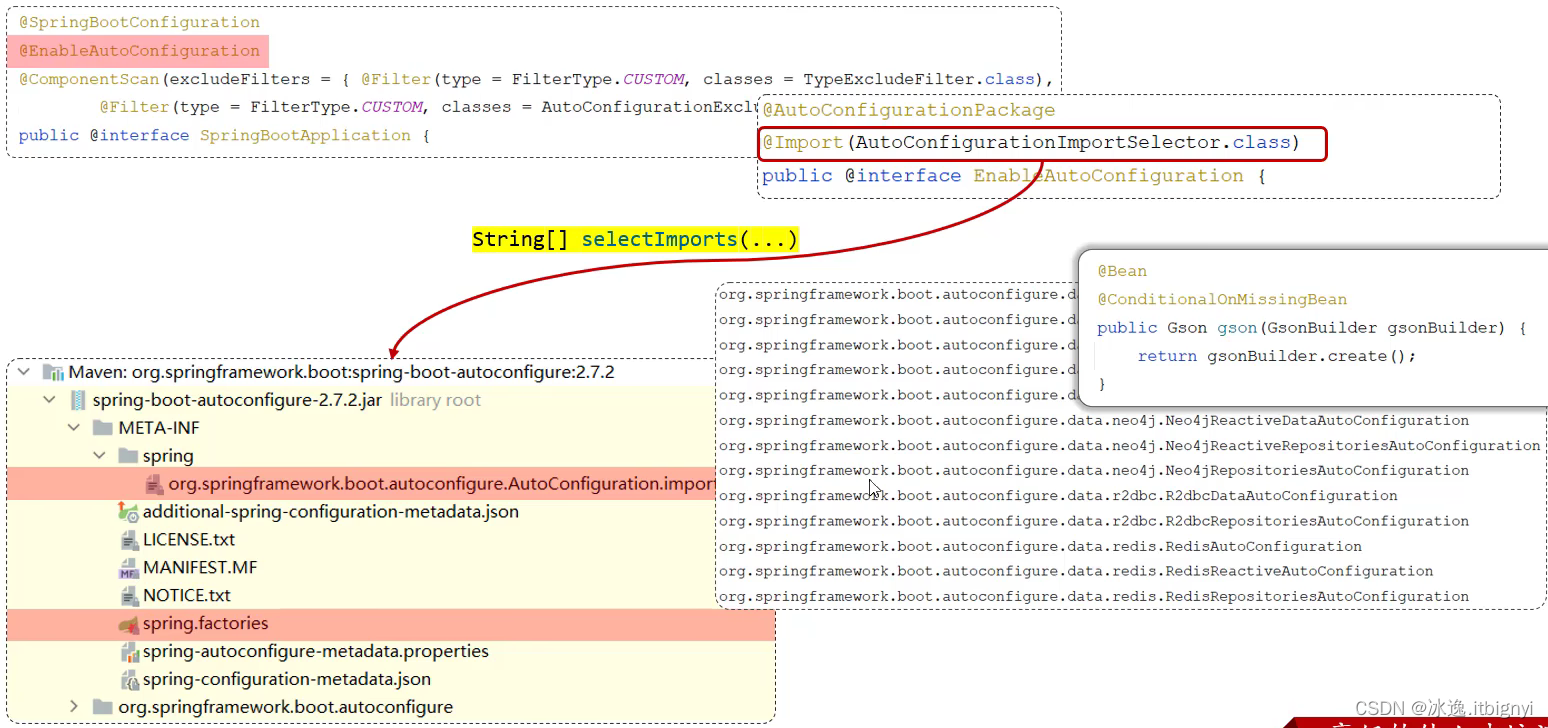
Spring boot原理
起步依赖 Maven的传递依赖 自动配置 Springboot的自动配置就是当spring容器启动后,一些配置类、bean对象就自动存入到IOC容器中,不需要我们手动去声明,从而简化了开发,省去了繁琐的配置操作。 自动配置原理: 方案一…...
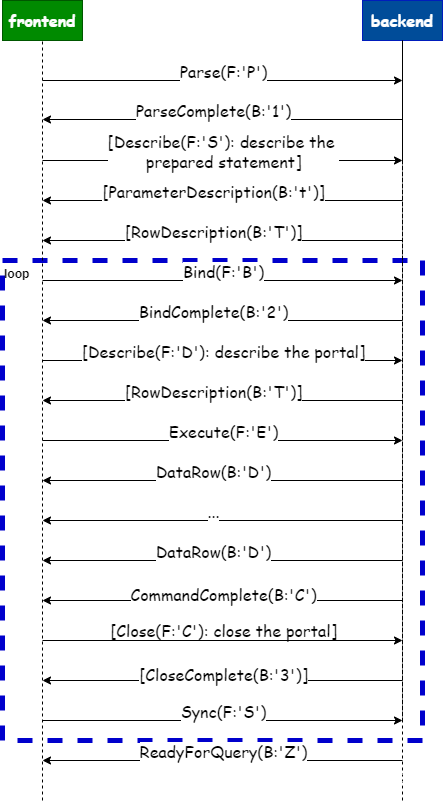
技术贴 | 深度解析 PostgreSQL Protocol v3.0(二)— 扩展查询
引言 PostgreSQL 使用基于消息的协议在前端(客户端)和后端(服务器)之间进行通信。该协议通过 TCP/IP 和 Unix 域套接字支持。 《深度解析 PostgreSQL Protocol v3.0》系列技术贴,将带大家深度了解 PostgreSQL Protoc…...
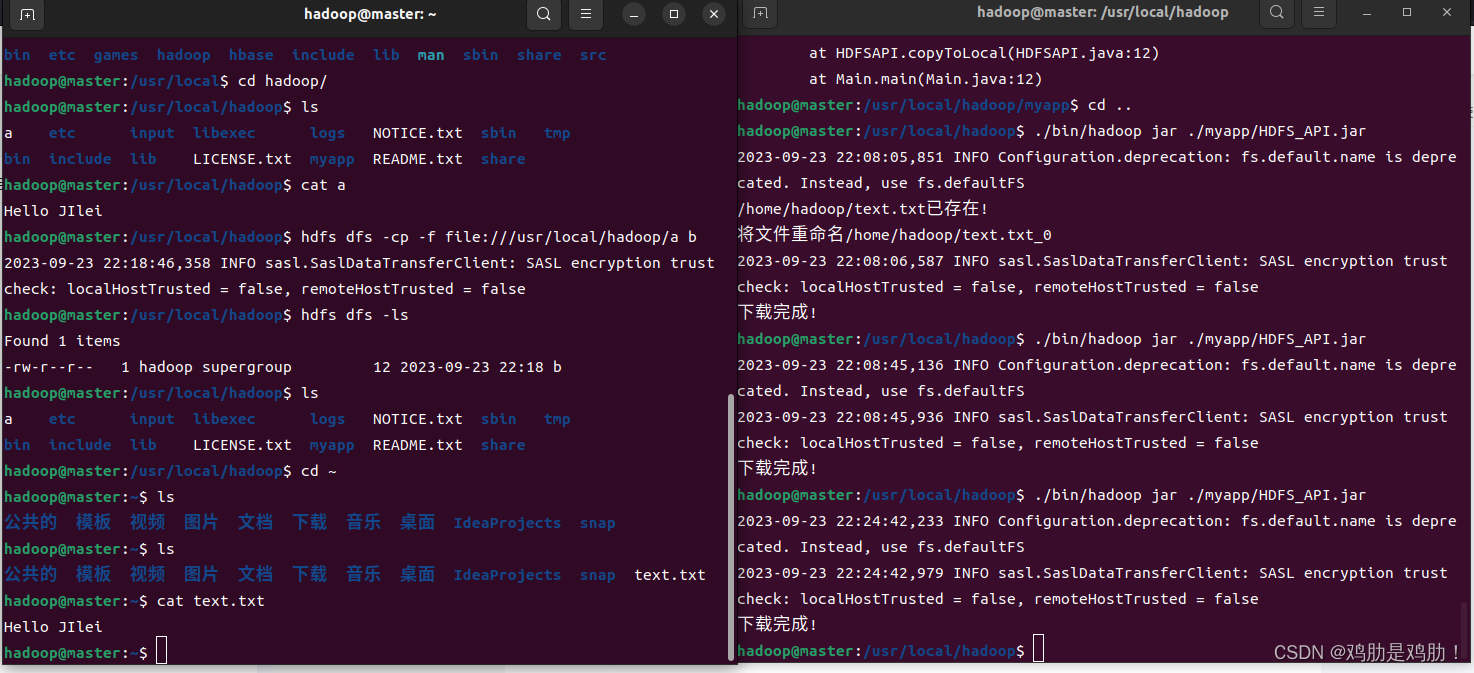
HDFS编程实践-从HDFS中下载指定文件到本地
前言:Hadoop采用java语言开发,提供了Java Api与HDFS进行交互 先要把hadoop的jar包导入到idea中去 为了能编写一个与hdfs交互的java应用程序,一般需要向java工程中添加以下jar包 1)/usr/local/hadoop/share/hadoop/common目录下…...

安防监控视频AI智能分析网关:人流量统计算法的应用场景汇总
TSINGSEE青犀人流量检测算法是内置在智能分析网关中的一种能够通过AI分析和计算人群数量以及密度的算法技术,在提升城市管理效率、改善用户体验和增加安全性方面发挥着重要作用。人流量检测算法在许多领域都有广泛的应用,如智慧城市、智慧交通、智慧景区…...

第一百五十二回 自定义组件综合实例:游戏摇杆三
文章目录 内容回顾优化性能示例代码我们在上一章回中介绍了 如何实现游戏摇杆相关的内容,本章回中将继续介绍这方面的知识.闲话休提,让我们一起Talk Flutter吧。 内容回顾 我们在前面章回中介绍了游戏摇杆的概念以及实现方法,并且通过示例代码演示了实现游戏摇杆的整个过程…...
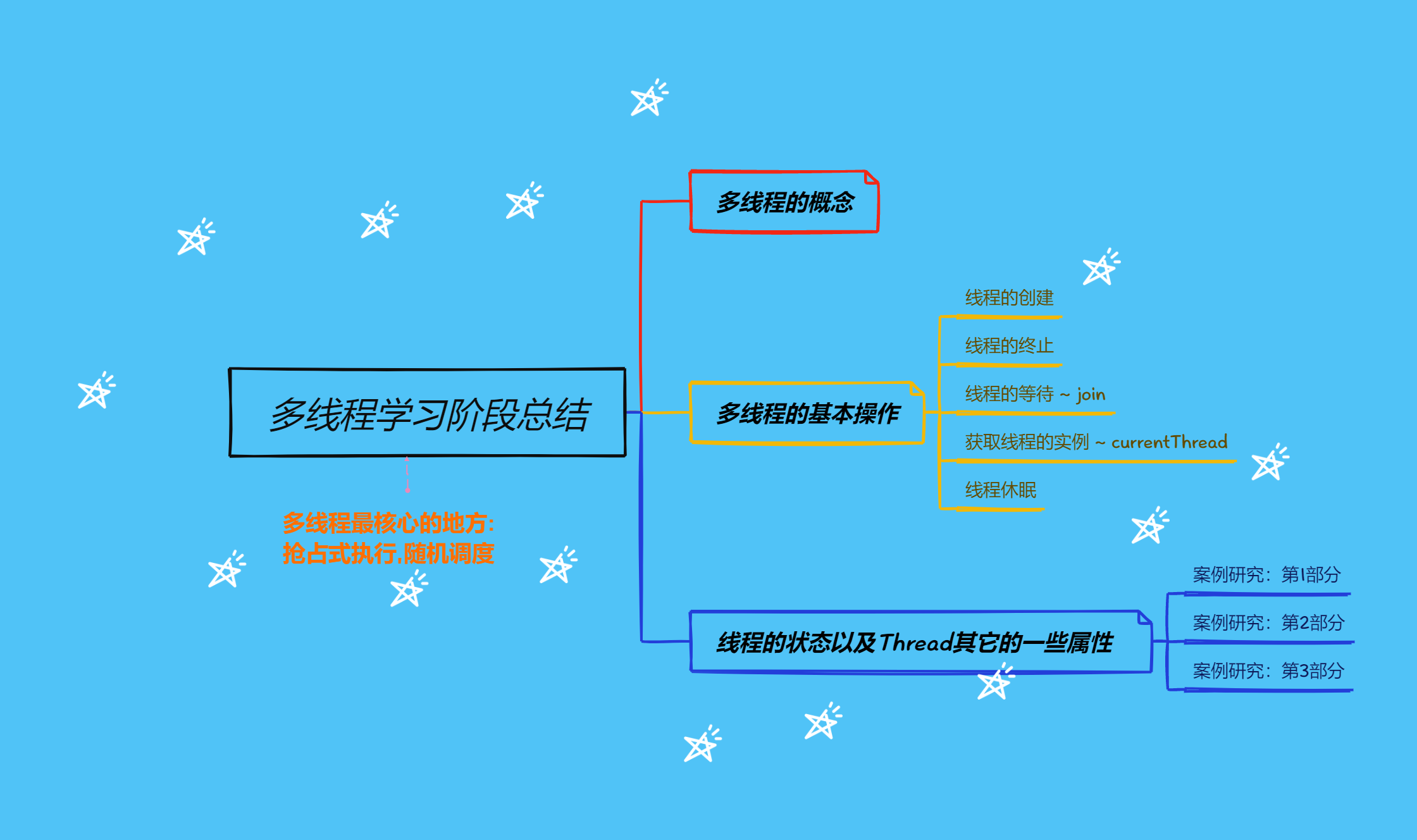
多线程的学习中篇上
终其一生,满是遗憾 知足且坚定,温柔且上进 总之岁月漫长,然而值得等待 获取当前线程引用 方法说明public static Thread currentThread();返回当前线程对象的引用 currentThread() > 在那个线程中, 就能获取到那个线程的实例. static关键…...

非标准化套利
交易对象:目前使用非标准化组合进行交易。(即黄金远近月,焦煤焦炭等等) 交易平台:易盛极星极星产品网 手续费研究:白糖期货手续费和保证金2023年09月更新 - 九期网 本人使用的期货交易公司:中信期货&…...

从CNN(卷积神经网络),又名CAM获取热图
一、说明 卷积神经网络(CNN)令人难以置信。如果你想知道它如何看待世界(图像),有一种方法是可视化它。 这个想法是,我们从最后的密集层中得到权重,然后乘以最终的CNN层。这需要全局平均…...
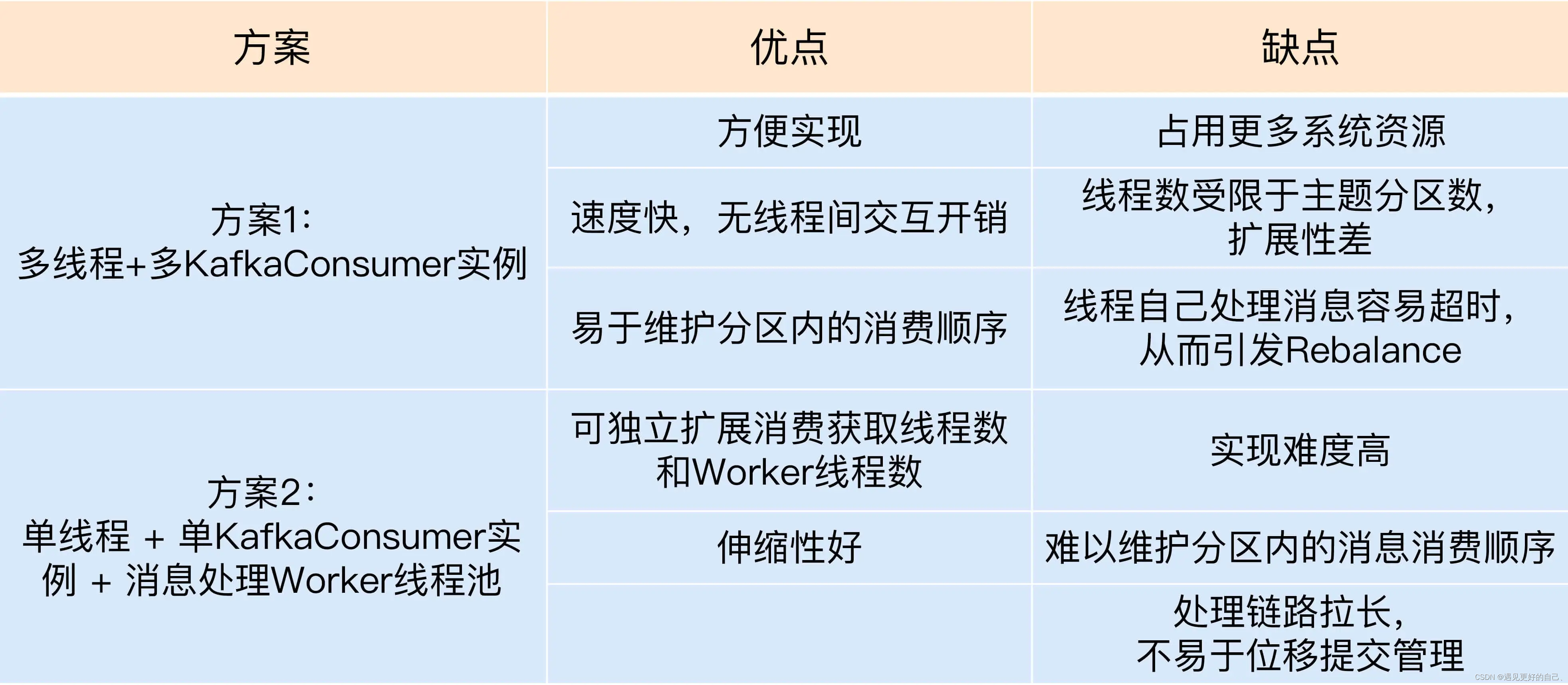
kafka消费者多线程开发
目录 前言 kafka consumer 设计原理 多线程的方案 参考资料 前言 目前,计算机的硬件条件已经大大改善,即使是在普通的笔记本电脑上,多核都已经是标配了,更不用说专业的服务器了。如果跑在强劲服务器机器上的应用程序依然是单…...

布局设计和实现:计算器UI【TableLayout、GridLayout】
一、使用TableLayout实现计算器UI 1.新建一个空白项目布局 根据自己的需求输入其他信息 填写完成后,点击Finish即可 2. 设计UI界面 在res/layout文件夹中的XML文件中创建UI界面。在这个XML文件中,您可以使用TableLayout来设计计算器界面。 2.1 创建l…...
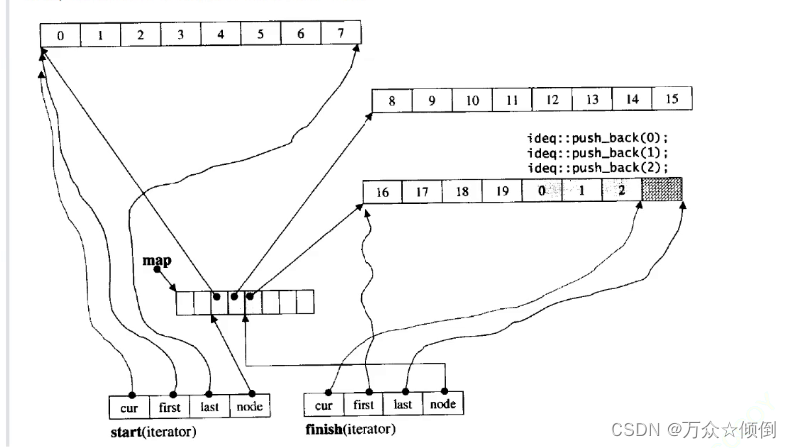
stack与queue的简单封装
前言: stack与queue即栈和队列,先进后出/先进先出的特性我们早已了然于心, 在学习数据结构时,我们利用c语言实现栈与队列,从结构体写起,利用数组或指针表示他们的数据成员,之后再一个个实现他们…...

ChatGPT使用技巧整理
目录 1. 让ChatGPT扮演专家角色2. 告诉ChatGPT你的身份3. 限制ChatGPT的回答长度4. 让ChatGPT一步步思考5. 明确你的要求和目的6. 提供充分的背景信息7. 始终结构化思考你的prompt1. 让ChatGPT扮演专家角色 当你们讨论的是市场营销问题时,你可以要求ChatGPT扮演一个具有20年从…...
机器学习笔记 - 维度诅咒的数学表达
1、点之间的距离 kNN分类器假设相似的点也可能有相同的标签。但是,在高维空间中,从概率分布中得出的点往往不会始终靠近在一起。 我们可以用一个简单的例子来说明这一点。 我们将在单位立方体内均匀地随机绘制点(如图所示),并研究该立方体内测试点的 k 个最近邻将占用多少…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
