工业蒸汽量预测(速通一)
工业蒸汽量预测(一)
- 赛题理解
- 1、评估指标
- 2、赛题模型
- 3、解题思路
- 理论知识
- 1、变量识别
- 2、变量分析
- 3、缺失值处理
- 4、异常值处理
- 5、变量转换
- 6、新变量生成
- 数据探索
- 1、导包
- 2、读取数据
- 3、查看数据
- 4、可视化数据分布
- 4.1箱型图
- 4.2获取异常数据并画图
- 4.3直方图和QQ图
- 4.4KDE分布图
- 4.5线性回归关系图
- 5、查看特征变量的相关性
- 5.1计算相关性系数
- 5.2画出相关性热力图
- 5.3筛选特征变量
- 5.4Box-Cox变换
赛题理解
1、评估指标
预测结果以均方误差MSE(Mean Squared Error)为评判标准,计算公式如下:
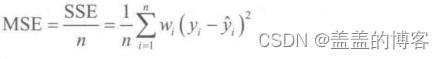
MSE是衡量“平均误差”的一种较为方便的方法。其值越小,说明预测模型描述实验数据具有越高的准确度,在sklearn中可以直接调用mean_squared_error()函数计算MSE,调用方法如下:

2、赛题模型
在机器学习中,根据问题类型的不同,常用的模型包括回归预测模型和分类预测模型。
回归问题:
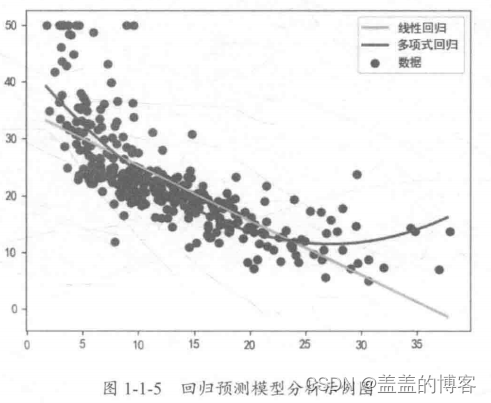
分类问题:

3、解题思路
在本赛题中,需要根据提供的V0~V37共38个特征变量来预测蒸汽量的数值,其预测值为连续型数值变量,故此问题为回归预测求解。
理论知识
1、变量识别
分清输入变量与输出变量,看清数据类型是字符型还是数值型,弄清楚连续型变量与类别型变量。
2、变量分析
2.1单变量分析
对于连续型变量,需要统计数据的中心分布趋势和变量的分布,如对下表中的数据进行分析:
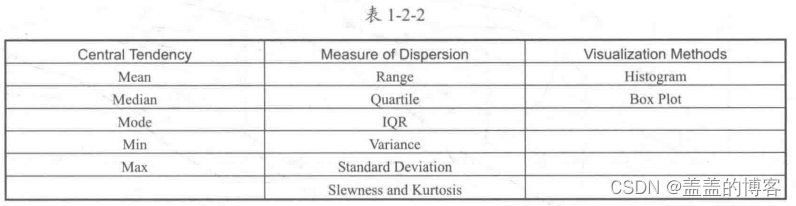
对于类别型变量,一般使用频次或占比表示每一个类别的分布情况,对应的衡量指标分别是类别变量的频次(次数)和频率(占比),可以用柱形图来表示可视化分布情况。
2.2双变量分析
使用双变量分析可以发现变量之间的关系。根据变量类型的不同,可以分为连续型与连续型、类别型与类别型、类别型与连续型三种双变量分析组合。
(1)连续型与连续型。绘制散点图和计算相关性是分析连续型与连续型双变量的常用方法。

一般来说, 在取绝对值后,0 ~ 0.09 为没有相关性,0.1 ~ 0.3 为弱相关,0.3 ~ 0.5 为中等相关,0.5 ~1.0为强相关。
(2)类别型与类别型。一般采用双向表、堆叠柱状图和卡方检验进行分析。
●双向表:这种方法是通过建立频次(次数)和频率(占比)的双向表来分析变量之间的关系,其中行和列分别表示一个变量,如表1-2-3 所示。
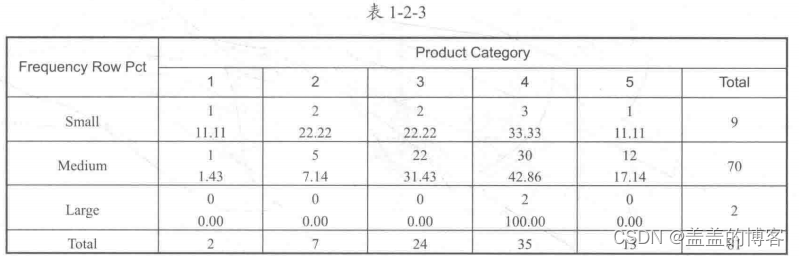
●堆叠柱状图:更直观

●卡方检验:主要用于两个和两个以上样本率(构成比)及两个二值型离散变量的关联性分析,即比较理论频次与实际频次的吻合程度或拟合优度。

(3)类别型与连续型。在分析类别型和连续型双变量时,可以绘制小提琴图(ViolinPlot),这样可以分析类别变量在不同类别时,另一个连续变量的分布情况。
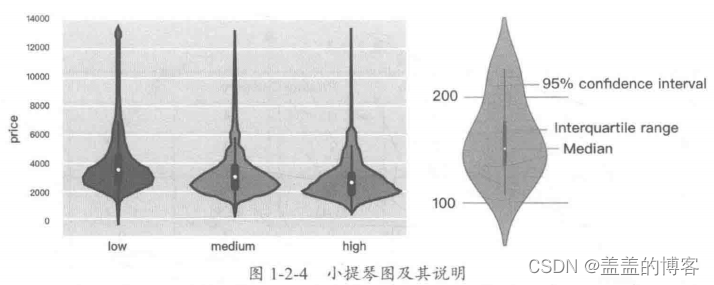
小提琴图结合了箱形图和密度图的相关特征信息,可以直观、清晰地显示数据的分布,常用于展示多组数据的分布及相关的概率密度。
说明:建议使用Seaborn包中的violinplot()函数。
3、缺失值处理
3.1删除: 分为成列删除和成对删除。

3.2平均值、众数、中值填充: 具体操作为一般填充和相似样本填充。
一般填充是用该变量下所有非缺失值的平均值或中值来补全缺失值。
相似样本填充是利用具有相似特征的样本的值或者近似值进行填充。
3.3预测模型填充: 通过建立预测模型来填补缺失值。在这种情况下,会把数据集分为两份:一份是没有缺失值的,用作训练集;另一份是有缺失值的,用作测试集。这样,缺失的变量就是预测目标,此时可以使用回归、分类等方法来完成填充。
当然,这种方法也有不足之处。首先,预测出来的值往往更加“规范”;其次,如果变量之间不存在关系,则得到的缺失值会不准确。
4、异常值处理
异常值对模型和预测分析的影响主要有增加错误方差,降低模型的拟合能力;异常值的非随机分布会降低正态性;与真实值可能存在偏差:影响回归、方差分析等统计模型的基本假设。
4.1 异常值检测
一般可以采用可视化方法进行异常值的检测,常用工县包括箱线图、直方图、散点图等。
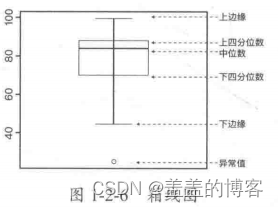
利用箱线图检测异常值的原则如下:
不在-1.5 * IQR和1.5 * IQR之间的样本点认为是异常值;
使用封顶方法可以认为在第5和第95百分位数范围之外的任何值都是异常值;
距离平均值为三倍标准差或更大的数据点可以被认为是异常值。
4.2 异常值处理
对异常值一般采用删除、转换、填充、区别对待等方法进行处理。
●删除: 如果是由输入误差、数据处理误差引起的异常值,或者异常值很小,则可以直接删除。
●转换: 数据转换可以消除异常值,如对数据取对数会减轻由极值引起的变化。
例如,图1-2-10所示即为取对数前后的数据分布直方图,可以看到转换后的数据分布更加均匀,没有明显的异常值。
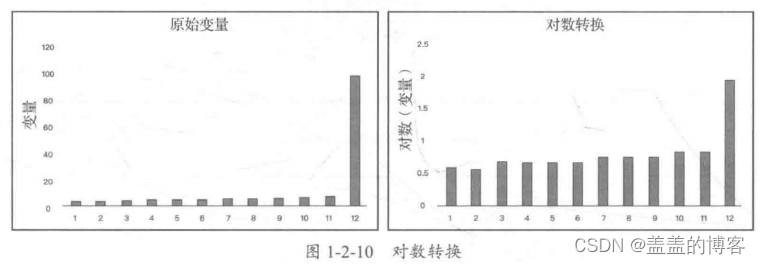
●填充:像处理缺失值一样,使用平均值、中值或其他的一些填补方法。在填补之前,需要分析异常值是自然形成的,还是人为造成的。如果是人为造成的,则可以进行填充处理,如使用预测模型填充。
● 区别对待:如果存在大量的异常值,则应该在统计模型中区别对待。其中一个方法是将数据分为两个不同的组,异常值归为一组,非异常值归为一组,且两组分别建立模型,然后最终将两组的输出合并。
5、变量转换
在使用直方图、核密度估计等工县对特征分布进行分析的过程中,我们可能会发现一些变量的取值分布不平均,这将会极大影响估计。为此,我们需要对变量的取值区间等进行转换,使其分布落在合理的区间内。

下面具体介绍几种常用的转换方法:
(1)对数变换: 对变量取对数,可以更改变量的分布形状。其通常应用于向右倾斜的分布,缺点是不能用于含有零或负值的变量。
(2)取平方根或立方根: 变量的平方根和立方根对其分布有波形的影响。取平方根可用于包括零的正值,取立方根可用于取值中有负值(包括零)的情况。
(3)变量分组: 对变量进行分类,如可以基于原始值、百分比或频率等对变量分类。例如,我们可以将收入分为高、中、低三类。其可以应用于连续型数据,超高维逻辑回归就是采取这种方式产生one-hot变量特征的。
6、新变量生成
变量生成是基于现有变量生成新变量的过程。生成的新变量可能与目标变量有更好的相关性,有助于进行数据分析。
如输入变量Date (dd-mm-yy, 日期),可以拆分生成新变量,日、月、年、周、工作日,也可能会发现与目标变量相关性更强的新变量。
有两种生成新变量的方法:
(1)创建派生变量: 指使用一组函数或不同方法从现有变量创建新变量。例如,在某个数据集中需要预测缺失的年龄值,为了预测缺失项的价值,我们可以提取名称中的称呼(Master,Mr, Miss, Mrs) 作为新变量。
(2)创建哑变量: 哑变量方法可将类别型变量转换为数值型变量。如Var. _Male (男性)和Var. Female (女性)这两个数值型变量,等效于类别型变量中的Gender (性别)。
数据探索
1、导包
2、读取数据
train_data_file = "./zhengqi_train.txt"
test_data_file = "./zhengqi_test.txt"train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
3、查看数据
查看训练集的统计信息:
train_data.describe()
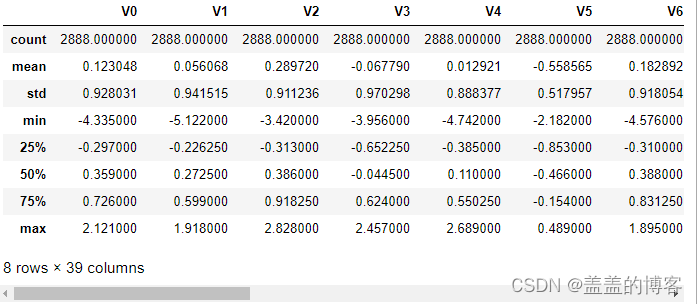
上面结果显示了数据的统计信息,如样本数、数据的均值(mean)、 标准差(std)、 最小值、最大值等。
4、可视化数据分布
4.1箱型图
fig = plt.figure(figsize=(4,6)) #指定绘图对象的宽度和高度
#sns.boxplot(train_data['V0'],orient="v",width=0.5) 图像是横着的
sns.boxplot(data=train_data['V0'],width=0.5)
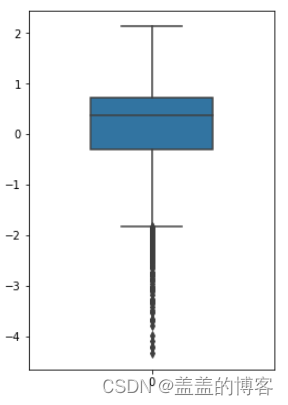
从图中可以看出有偏离值,许多数据点位于下四分位点以下。
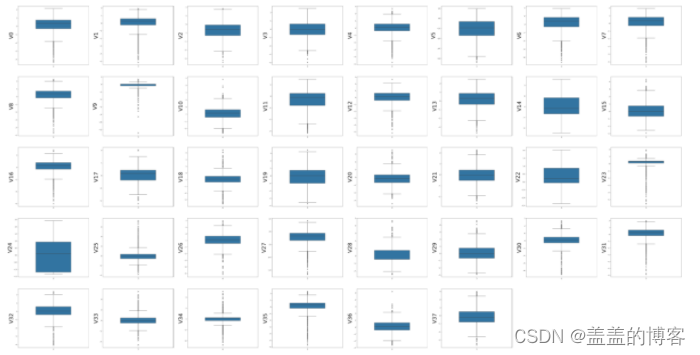
然后绘制训练集中变量V0~V37的箱形图:
column = train_data.columns.tolist()[:39] #列表头
fig = plt.figure(figsize=(80,60),dpi=75) #指定绘图对象的宽度和高度
for i in range(38):plt.subplot(7,8,i+1) #7行8列子图sns.boxplot(data=train_data[column[i]],width=0.5) #箱式图plt.ylabel(column[i],fontsize=36)
plt.show()
plt.figure(figsize=(18,10))
plt.boxplot(x=train_data.values,labels=train_data.columns)
plt.hlines([-7.5,7.5],0,40,colors='r')
plt.show()
#另一种方法,用plt自带的方法画箱型图
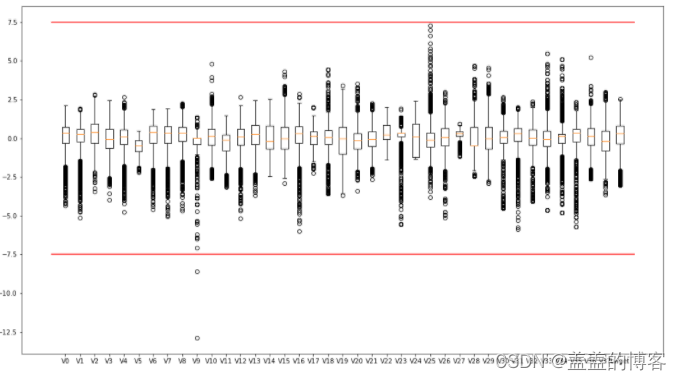
4.2获取异常数据并画图
此方法是采用模型预测的形式找出异常值。
#function to detect outliers based on the predictions of a model
def find_outliers(model,X,y,sigma=3):#predict y values using modeltry:y_pred = pd.Series(model.predict(X),index=y.index)#if predicting fails,try fitting the model firstexcept:model.fit(X,y)y_pred = pd.Series(model.predict(X),index=y.index)#calculate residuals between the model prediction and true y values resid = y - y_predmean_resid = resid.mean()std_resid = resid.std()#calculate z statistic, define outliers to be where |z| > sigmaz = (resid - mean_resid)/std_residoutliers = z[abs(z)>sigma].index#print and plot the resultsprint('R2=',model.score(X,y))print('mse=',mean_squared_error(y,y_pred))print('---------------------------------')print('mean of residuals:',mean_resid)print('std of residuals:',std_resid)print('---------------------------------')print(len(outliers),'outliers:')print(outliers.tolist())plt.figure(figsize=(15,5))ax_131 = plt.subplot(1,3,1)plt.plot(y,y_pred,'.')plt.plot(y.loc[outliers],y_pred.loc[outliers],'ro')plt.legend(['Accepted','Outliers'])plt.xlabel('y')plt.ylabel('y_pred');ax_132=plt.subplot(1,3,2)plt.plot(y,y-y_pred,'.')plt.plot(y.loc[outliers],y.loc[outliers]-y_pred.loc[outliers],'ro')plt.legend(['Accepted','Outliers'])plt.xlabel('y')plt.ylabel('y-y_pred');ax_133=plt.subplot(1,3,3)z.plot.hist(bins=50,ax=ax_133)z.loc[outliers].plot.hist(color='r',bins=50,ax=ax_133)plt.legend(['Accepted','Outliers'])plt.xlabel('z')plt.savefig('outliers.png')return outliers
#通过岭回归模型找出异常值,并绘制其分布
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
X_train=train_data.iloc[:,0:-1]
y_train=train_data.iloc[:,-1]
outliers = find_outliers(Ridge(),X_train, y_train)
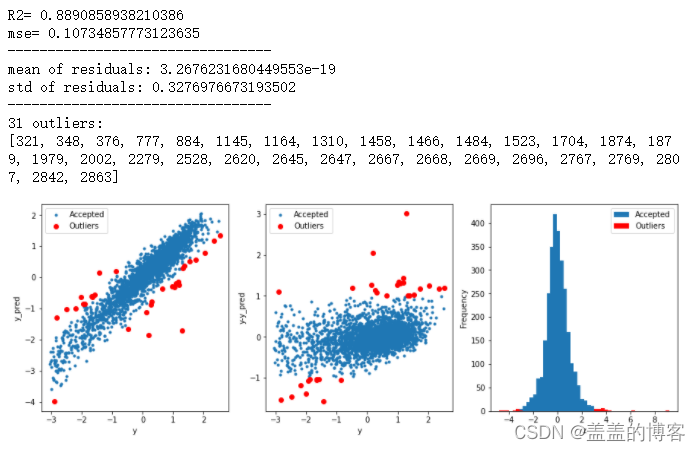
4.3直方图和QQ图
Q-Q图是指数据的分位数和正态分布的分位数对比参照的图,如果数据符合正态分布,则所有的点都会落在直线上。
首先,通过绘制特征变量V0的直方图查看其在训练集中的统计分布,并绘制Q-Q图查看V0的分布是否近似于正态分布。
plt.figure(figsize=(10,5))ax=plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax=plt.subplot(1,2,2)
res=stats.probplot(train_data['V0'],plot=plt)
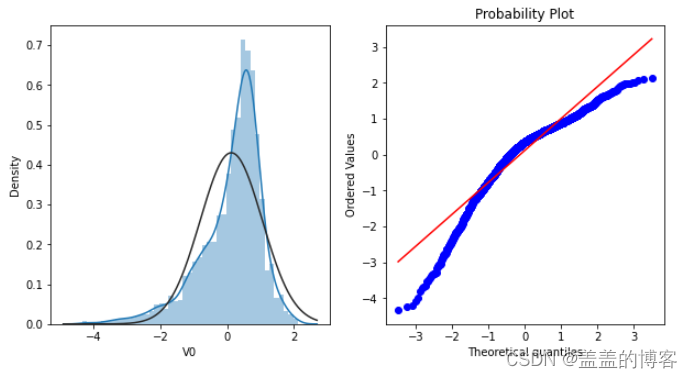
可以看到,训练集中特征变量V0的分布不是正态分布。
然后,绘制训练集中所有变量的直方图和Q-Q图。
train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4*train_cols,4*train_rows))i=0
for col in train_data.columns:i+=1ax=plt.subplot(train_rows,train_cols,i)sns.distplot(train_data[col],fit=stats.norm)i+=1ax=plt.subplot(train_rows,train_cols,i)res=stats.probplot(train_data[col],plot=plt)
plt.tight_layout()
plt.show()
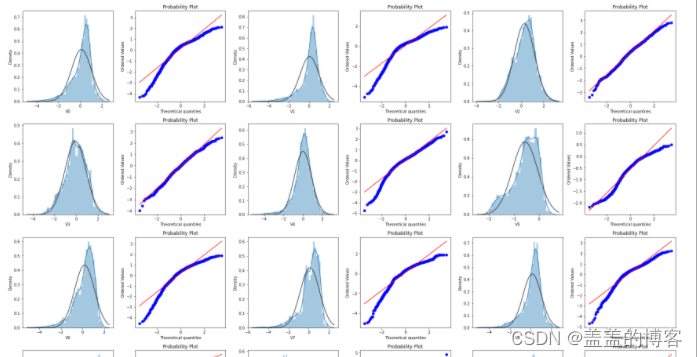
从数据分布图可以发现,很多特征变量(如V1,V9,V24,V28等)的数据分布不是正态的,
数据并不跟随对角线分布,后续可以使用数据变换对其进行处理。
4.4KDE分布图
KDE ( Kernel Density Estimation,核密度估计)可以理解为是对直方图的加窗平滑。通过绘制KDE分布图,可以查看并对比训练集和测试集中特征变量的分布情况,发现两个数据集中分布不一致的特征变量。
首先对比同一特征变量V0在训练集和测试集中的分布情况,并查看数据分布是否–致。
plt.figure(figsize=(8,4),dpi=150)
ax = sns.kdeplot(train_data['V0'],color="Red", shade=True)
ax = sns.kdeplot(test_data['V0'],color="Blue", shade=True)
ax.set_xlabel('V0')
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])
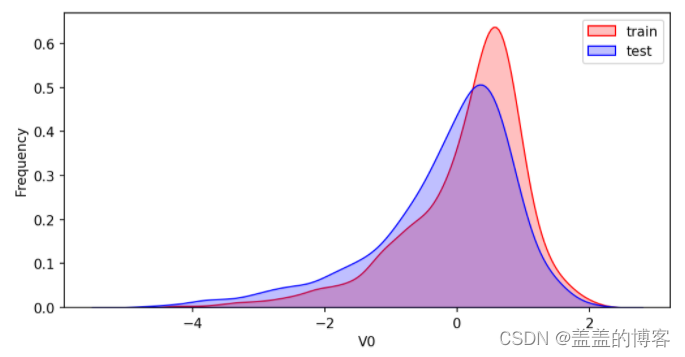
可以看到,V0在两个数据集中的分布基本一致。
然后,对比所有变量在训练集和测试集中的KDE分布。
dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4 * dist_cols, 4 * dist_rows))
i = 1
for col in test_data.columns:ax = plt.subplot(dist_rows,dist_cols,i)ax = sns.kdeplot(train_data[col],color="Red",shade=True)ax = sns.kdeplot(test_data[col],color="Blue",shade=True)ax.set_xlabel(col)ax.set_ylabel("Frequency")ax = ax.legend(["train","test"])i += 1
plt.show()
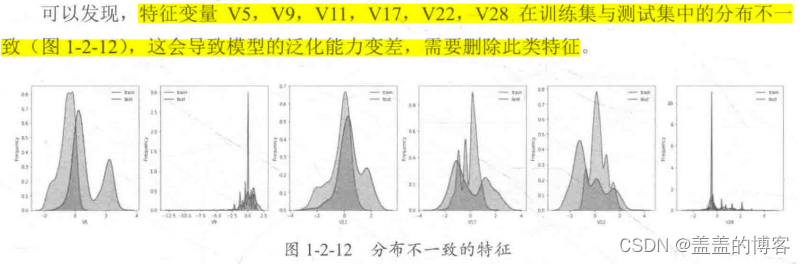
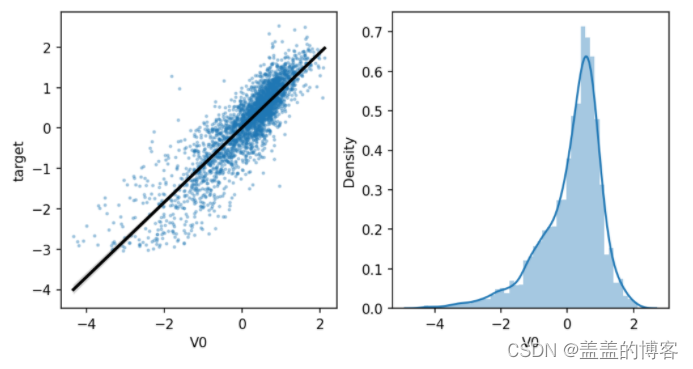
4.5线性回归关系图
fcols = 2
frows = 1
plt.figure(figsize=(8,4),dpi=150)ax=plt.subplot(1,2,1)
sns.regplot(x='V0',y='target',data=train_data,ax = ax,scatter_kws={'marker':'.','s':3,'alpha':0.3},line_kws={'color':'k'});
plt.xlabel('V0')
plt.ylabel('target')ax=plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')plt.show()
5、查看特征变量的相关性
5.1计算相关性系数
在删除训练集和测试集中分布不一致的特征变量,如V5,V9, V11, V17, V22,V28之后,计算剩余特征变量及target变量的相关性系数。
pd.set_option('display.max_columns',10)
pd.set_option('display.max_rows',10)
data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28'],axis=1)train_corr = data_train1.corr()
train_corr
5.2画出相关性热力图
ax=plt.subplots(figsize=(20,16)) #调整画布大小
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True) #画热力图
5.3筛选特征变量
根据相关系数筛选K个最相关的特征变量:
k = 10
cols = train_corr.nlargest(k,'target')['target'].indexcm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10,10)) #调整画布大小
hm = sns.heatmap(train_data[cols].corr(),annot=True, square = True)
plt.show()
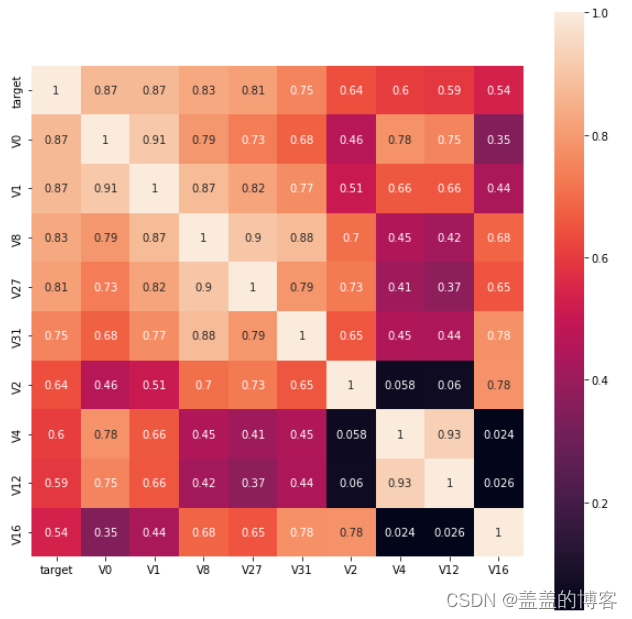
找出相关系数>0.5的特征变量:
threshold = 0.5corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat["target"]) > threshold]
plt.figure(figsize=(10,10))
g = sns.heatmap(train_data[top_corr_features].corr(),annot = True,cmap="RdYlGn")
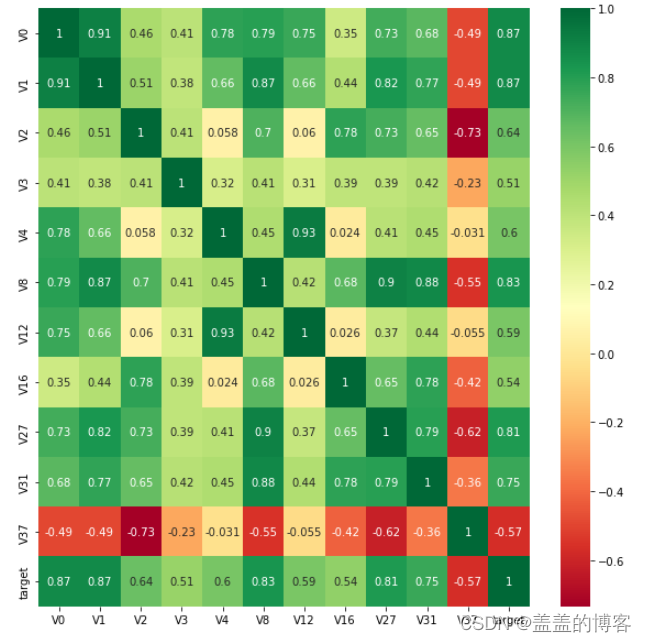
可以将一些不重要的特征删除,方便快速分析重要特征。
说明:相关性选择主要用于判别线性相关,对于target变量如果存在更复杂的函数形式的影响,则建议使用树模型的特征重要性去选择。
5.4Box-Cox变换
由于线性回归是基王正态分布的,因此在进行统计分析时,需要将数据转换使其符合正态分布。
Box-Cox变换是统计建模中常用的一种数据转换方法。在连续的响应变量不满足正态分布时,可以使用Box-Cox变换,这一变换可以使线性回归模型在满足线性、正态性、独立性及方差齐性的同时,又不丢失信息。在对数据做Box-Cox变换之后,可以在一定程度上减小不可观测的误差和预测变量的相关性,这有利于线性模型的拟合及分析出特征的相关性。
在做Box-Cox变换之前,需要对数据做归一化预处理。在归一化时,对数据进行合并操作可以使训练数据和测试数据一致。这种方式可以在线下分析建模中使用,而线上部署只需采用训练数据的归一化即可。
#pandas归一化
cols_numeric = list(X_train.columns)def scale_minmax(col):return(col-col.min())/(col.max()-col.min())X_train_s = X_train[cols_numeric].apply(scale_minmax,axis = 0)
X_train_s.describe()
#sklearn归一化
from sklearn import preprocessingfeatures_columns = list(X_train.columns)
min_max_scaler = preprocessing.MinMaxScaler()
min_max_scaler = min_max_scaler.fit(X_train[features_columns])X_train_scaler = pd.DataFrame(min_max_scaler.transform(X_train[features_columns]))
X_test_scaler = pd.DataFrame(min_max_scaler.transform(X_test[features_columns]))
X_test_data_scaler = pd.DataFrame(min_max_scaler.transform(test_data[features_columns]))
对特征变量做Box-Cox变换后,计算分位数并画图展示(基于正态分布),显示特征变量与target变量的线性关系。示例代码如下:
fcols = 6
frows = len(cols_numeric_left)
plt.figure(figsize=(4*fcols,4*frows))
i = 0for var in cols_numeric_left:dat = train_data_process[[var,'target']].dropna()i += 1plt.subplot(frows,fcols,i)sns.distplot(dat[var], fit = stats.norm)plt.title(str(var) + 'Original')plt.xlabel('')i += 1plt.subplot(frows,fcols,i)_ = stats.probplot(dat[var],plot = plt)plt.title('skew' + '{:.4f}'.format(stats.skew(dat[var])))plt.xlabel('')plt.ylabel('')i += 1plt.subplot(frows,fcols,i)plt.plot(dat[var],dat['target'],'.',alpha = 0.5)plt.title('corr=' + '{:.2f}'.format(np.corrcoef(dat[var],dat['target'])[0][1]))i += 1plt.subplot(frows,fcols,i)trans_var,lambda_var = stats.boxcox(dat[var].dropna() + 1)trans_var = scale_minmax(trans_var)sns.distplot(trans_var,fit=stats.norm)plt.title(str(var) + 'Tramsformed')plt.xlabel('')i += 1plt.subplot(frows,fcols,i)_ = stats.probplot(trans_var,plot = plt)plt.title('skew=' + '{:.4f}'.format(stats.skew(trans_var)))plt.xlabel('')plt.ylabel('')i += 1plt.subplot(frows,fcols,i)plt.plot(trans_var,dat['target'],'.',alpha = 0.5)plt.title('corr=' + '{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))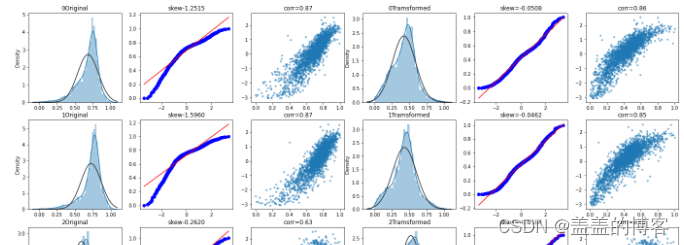
可以发现,经过变换后,变量分布更接近正态分布,而且从图中可以更加直观地看出特
征变量与target变量的线性相关性。
相关文章:

工业蒸汽量预测(速通一)
工业蒸汽量预测(一) 赛题理解1、评估指标2、赛题模型3、解题思路 理论知识1、变量识别2、变量分析3、缺失值处理4、异常值处理5、变量转换6、新变量生成 数据探索1、导包2、读取数据3、查看数据4、可视化数据分布4.1箱型图4.2获取异常数据并画图4.3直方图…...

机器学习的主要内容
分类任务 回归任务 有一些算法只能解决回归问题有一些算法只能解决分类问题有一些算法的思路既能解决回归问题,又能解决分类问题 一些情况下, 回归任务可以转化为分类任务, 比如我们预测学生的成绩,然后根据学生的成绩划分为A类、…...
)
华为OD机试真题-分积木-2023年OD统一考试(B卷)
题目描述: Solo和koko是两兄弟,妈妈给了他们一大堆积木,每块积木上都有自己的重量。现在他们想要将这些积木分成两堆。哥哥Solo负责分配,弟弟koko要求两个人获得的积木总重量“相等”(根据Koko的逻辑),个数可以不同,不然就会哭,但koko只会先将两个数转成二进制再进行加…...

SpringBoot自动装配原理及分析
一、什么是自动装配 在使用SpringBoot的时候,会自动将Bean装配到IoC容器中。例如我们在使用Redis数据库的时候,会引入依赖spring-boot-starter-data-redis。在引入这个依赖后,服务初始化的时候,会将操作Redis需要的组件注入到IoC…...
Android开发笔记 :理解Fragment
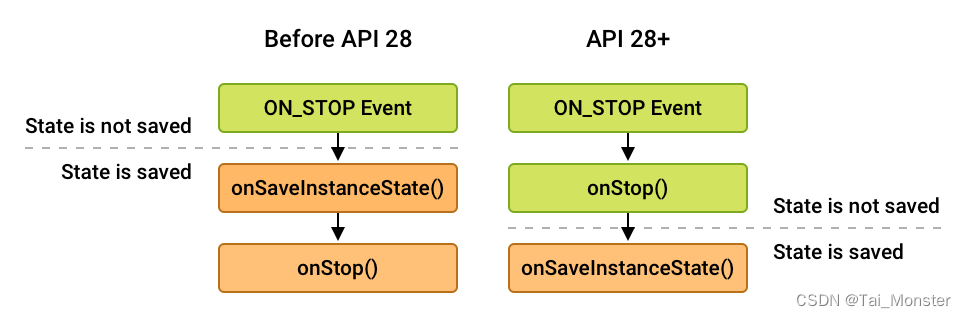
Android开发笔记:理解Fragment 导言 本篇文章产生的原因很简单,就是我在了解Android Jetpack中的Lifecycle框架时发现Lifecycle具体时间和状态的更新都是由一个名为ReportFragment的Fragment来跟踪的,为了更好的了解Fragment是如何追踪Activ…...

std::chrono获取当前秒级/毫秒级/微秒级/纳秒级时间戳
当前时间戳获取方法 先使用std::chrono获取当前系统时间,然后将当前系统时间转换为纪元时间std::time_t类型,之后使用std::localtime对std::time_t类型转换为本地时间结构体std::tm类型,最后使用strftime对时间进行格式化输出。 其中std::t…...

sh文件介绍及linux下执行
Shell脚本是一种用于自动化任务和系统管理的脚本语言。它允许用户通过命令行界面执行一系列命令,从而简化了重复性任务的处理过程。 以下是关于Shell脚本的一些基本概念: 1. Shell脚本通常以“.sh”扩展名保存,例如“script.sh”。 2. Shell…...

js-cookie使用 js深度克隆(判断引用类型是数组还是对象的方法)
cookie和深度拷贝的使用 1、js-cookie使用2、js深度克隆 1、js-cookie使用 前端的本地存储分为 localstorage、sesstionstorage、cookie 但是咱们有时候需要做7天免登录的需求时,选择 cookie 作为前端的本地存储是在合适不过的了 直接操作 cookie 可以, …...

[Pytorch]语义分割任务分类的实现
文章目录 [Pytorch]语义分割任务分类的实现 [Pytorch]语义分割任务分类的实现 假如我们定义了一个网络用于语义分割任务,这个网络简称为model() 语义分割任务要做的是: 对于一个图片输入input,大小为(B,C,…...
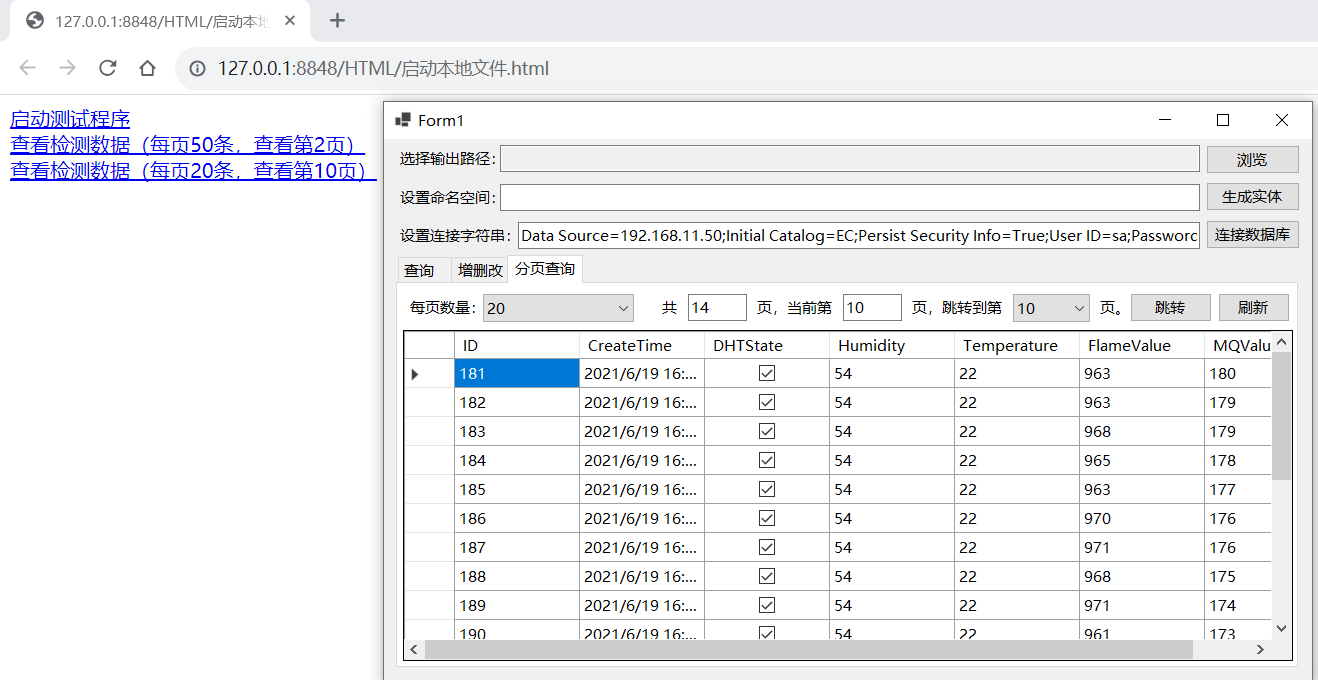
测试网页调用本地可执行程序(续:带参数调用)
前篇文章介绍了网页调用本地可执行程序的方式,通过在注册表中注册命令,然后在网页中调用命令启动本地程序。如果需要传递参数,则需要在注册表命令中的command项中设置如下形式的值。 "XXXXXX\XXXXXXX.exe" "%1"&emsp…...

Carla自动驾驶模拟器安装和使用
Carla自动驾驶模拟器安装和使用 1 安装 ubuntu20.04安装carla0.9.11版本 步骤1:打开下面链接,点击第一个[Ubuntu] CARLA_0.9.11.tar.gz carla-0.9.11源码下载 步骤2:下载完解压到/opt目录下 我的话是先在下载目录上提取解压,然…...
【每日一题】1539. 第 k 个缺失的正整数
1539. 第 k 个缺失的正整数 - 力扣(LeetCode) 给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。 请你找到这个数组里第 k 个缺失的正整数。 示例 1: 输入:arr [2,3,4,7,11], k 5 输出:9 解释:缺失…...

AI-Chat,一款集全网ai功能的应用(附下载链接)
AI-Chat是一款综合性的聊天机器人,集成了多种先进的模型和功能。它采用了GPT4.0、联网版GPT和清华模型等多种模型,使得其具备更强大的语言处理能力。同时,AI-Chat还融合了AI绘画模型,例如Stable Diffusion绘画、文生图、图生图、艺…...

3、靶场——Pinkys-Place v3(3)
文章目录 一、获取flag41.1 关于SUID提权1.2 通过端口转发获取setuid文件1.3 运行pinksecd文件1.4 利用nm对文件进行分析1.5 构建payload1.6 Fire 二、获取flag52.1 生成ssh公钥2.2 免密登录ssh2.3 以pinksecmanagement的身份进行信息收集2.4 测试程序/usr/local/bin/PSMCCLI2.…...
什么是 AirServer?Mac专用投屏工具AirServer 7 .27 for Mac中文破解版百度网盘下载
AirServer 7 .27 for Mac中文免费激活版是一款Mac专用投屏工具,能够通过本地网络将音频、照片、视频以及支持AirPlay功能的第三方App,从 iOS 设备无线传送到 Mac 电脑的屏幕上,把Mac变成一个AirPlay终端的实用工具。 目前最新的AirServer 7.2…...

MapStruct介绍以及VO、DTO、PO、DO的区别
文章目录 一.基本概念1.1VO**(Value Object)值对象**1.2DTO**(Data Transfer Object)数据传输对象**1.3 PO**(Persistant Object)持久对象**等同于Entity,这俩概念是一致的 或DO1.4 **BO&#x…...

记一次hyperf框架封装swoole自定义进程
背景 公司准备引入swoole和rabbitmq来处理公司业务。因此,我引入hyperf框架,想用swoole的多进程来实现。 自定义启动服务封装 <?php /*** 进程启动服务【manager】*/ declare(strict_types1);namespace App\Command;use Swoole; use Swoole\Proce…...

多输入多输出 | MATLAB实现GA-BP遗传算法优化BP神经网络多输入多输出
多输入多输出 | MATLAB实现GA-BP遗传算法优化BP神经网络多输入多输出 目录 多输入多输出 | MATLAB实现GA-BP遗传算法优化BP神经网络多输入多输出预测效果基本介绍程序设计往期精彩参考资料 预测效果 基本介绍 多输入多输出 | MATLAB实现GA-BP遗传算法优化BP神经网络多输入多输出…...

李宏毅机器学习笔记-transformer
transformer是什么呢?是一个seq2seq的model。具体应用如上图所示,输入和输出的序列长度不固定,由model自己决定。 语音翻译指的是,直接输入一段语音信号,例如英文,输出的直接是翻译之后的中文。 seq2seq如…...
基于Java的酒店管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...

记一次spark在docker本地启动报错
1,背景 在docker中部署spark服务和调用spark服务的微服务,微服务之间通过fegin调用 2,问题,docker容器中服务器来后,注册中心都有,调用服务也正常,但是调用spark启动任务后报错,报错…...
