113双周赛
题目列表
2855. 使数组成为递增数组的最少右移次数
2856. 删除数对后的最小数组长度
2857. 统计距离为 k 的点对
2858. 可以到达每一个节点的最少边反转次数
一、使数组成为递增数组的最少右移次数

这题可以直接暴力求解,枚举出每种右移后的数组,将它和排完序后的数组比较,时间复杂度为O(n^2)
代码如下
class Solution {
public:int minimumRightShifts(vector<int>& nums) {vector<int> v=nums;sort(v.begin(),v.end());for(int i=0;i<nums.size();i++){if(v==nums) return i;nums.insert(nums.begin(),nums.back());nums.pop_back();}return -1;}
};这个能过,但是有没有更快的算法,我们观察一下这个数组,如果它要是能右移成递增数组,那么它必然是由两个递增数组构成的,且前一个数组的最小值,一定大于后一个数组的最大值,答案就是第二个数组的长度,所以我们只要试着将数组拆分成两个递增数组就行(边界条件挺多,一定要细节),时间复杂度为O(n)
代码如下
class Solution {
public:int minimumRightShifts(vector<int>& nums) {int end1=0,n=nums.size();while(end1+1<n&&nums[end1]<nums[end1+1])end1++;if(end1==n-1) return 0;int end2=end1+1;while(end2+1<n&&nums[end2]<nums[end2+1])end2++;if(end2!=n-1||nums[0]<nums[n-1]) return -1;else return n-end1-1;}
};二、删除数对后的最小数组长度

这题还是比较难想到的,比较绕。我们需要多枚举几个例子,然后就会发现,当某个数的个数cnt大于等于数组长度n的一半时,最优的方案就是将它前后的数都与它相互抵消(因为如果还让其他数相互抵消,那么剩余的和该数相抵消的元素个数就会变小,从而该元素剩下的个数就会变多),所以答案就是cnt-(n-cnt)=2*cnt-n,那么如果没有一个数的个数大于数组长度的一半呢?
首先从最特殊的数组中数字都是唯一的情况开始讨论,那么显然,当数组长度为偶数时,答案为0,当数组长度为奇数时,答案为1,那么是不是所有的情况都符合这个规律呢?答案是,确实都符合这个规律,因为所有的数的个数都<n/2,那么我们就可以通过抵消,将数的个数全部化成1
代码如下
class Solution {
public:int minLengthAfterRemovals(vector<int>& nums) {unordered_map<int,int>cnt;int n=nums.size(),ans=n&1;//n&1,奇数为1,偶数为0for(auto x:nums)++cnt[x];for(auto [x,y]:cnt)if(y>n/2)ans=max(ans,2*y-n);return ans;}
};当然这题如果想不到这么深,那么也可以用最基本的贪心,每次拿出出现次数最大的两个元素相抵消,直到剩下零个数或剩下一个数为止。代码如下
class Solution {
public:int minLengthAfterRemovals(vector<int>& nums) {unordered_map<int,int>cnt;int n=nums.size(),ans=n&1;for(auto x:nums)++cnt[x];priority_queue<int>q;for(auto [x,y]:cnt)q.push(y);while(q.size()>1){int x=q.top();q.pop();int y=q.top();q.pop();x--,y--;if(x)q.push(x);if(y)q.push(y);}return q.empty()?0:q.top();}
};三、统计距离为k的点对

看到两个数的和k,以及k的数据范围,我们就要想到这题能用暴力枚举点来做,然后通过枚举到的点,求出与之相对应的点的坐标,答案加上之前出现的该点个数(用哈希表统计),代码如下
class Solution {
public:int countPairs(vector<vector<int>>& coordinates, int k) {int n=coordinates.size();unordered_map<long long,int>cnt;int ans=0;for(auto& e:coordinates){int x=e[0],y=e[1];for(int i=0;i<=k;i++){auto it=cnt.find((x^i)*1000000LL+(y^(k-i)));if(it!=cnt.end())ans+=it->second;}cnt[x*1000000LL+y]++;}return ans;}
};四、可以到达每一个节点的最小边反转次数

这题是换根dp,即通过根节点的最小边反转次数,来得到它孩子结点的最小边反转次数,因为它的孩子结点的反转边的个数就和它父节点的最小边反转次数相差一个它俩之间的边是否需要翻转,其它的都一样。
代码如下
class Solution {
public:vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {//建图vector<vector<pair<int,int>>>g(n);for(auto& e:edges){int x=e[0],y=e[1];g[x].push_back({y,1});//顺便记录一下边的方向,1为正,-1为逆g[y].push_back({x,-1});}vector<int>ans(n);//计算根节点的最少边反转次数function<void(int,int)>dfs=[&](int x,int fa){for(auto& [y,dir]:g[x]){if(y!=fa){ans[0]+=(dir<0);//方向反的需要反转dfs(y,x);}}};dfs(0,-1);//换根dpfunction<void(int,int)>reroot=[&](int x,int fa){for(auto& [y,dir]:g[x]){if(y!=fa){ans[y]=ans[x]+dir;reroot(y,x);}}};reroot(0,-1);return ans;}
};相关文章:

113双周赛
题目列表 2855. 使数组成为递增数组的最少右移次数 2856. 删除数对后的最小数组长度 2857. 统计距离为 k 的点对 2858. 可以到达每一个节点的最少边反转次数 一、使数组成为递增数组的最少右移次数 这题可以直接暴力求解,枚举出每种右移后的数组,将…...
React 全栈体系(九)
第五章 React 路由 一、相关理解 1. SPA 的理解 单页 Web 应用(single page web application,SPA)。整个应用只有一个完整的页面。点击页面中的链接不会刷新页面,只会做页面的局部更新。数据都需要通过 ajax 请求获取, 并在前端…...
阈值化分割,对灰度级图像进行二值化处理(数字图像处理大题复习 P8)
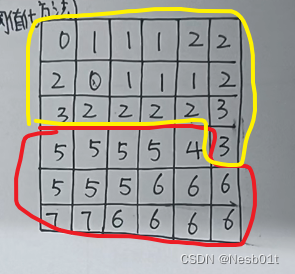
文章目录 画出表格求出灰度直方图 & 山谷画出结果图 画出表格 有几个0就写几,有几个1就写几,如图 求出灰度直方图 & 山谷 跟前面求灰度直方图的方法一样,找出谷底,发现结果为 4 画出结果图 最终的结果就是…...

vue3中withDefaults是什么
问: const props withDefaults(defineProps<{// 数据列表lotteryList: { pic: string; name?: string }[];// 中奖idwinId: number;// 抽奖初始转动速度initSpeed: number;// 抽奖最快转动速度fastSpeed: number;// 抽奖最慢转动速度slowSpeed: number;// 基本圈数baseCi…...
Android进阶之路 - 盈利、亏损金额格式化
在金融类型的app中,关于金额、数字都相对敏感和常见一些,在此仅记录我在金融行业期间学到的皮毛,如后续遇到新的场景也会加入该篇 该篇大多采用 Kotlin 扩展函数的方式进行记录,尽可能熟悉 Kotlin 基础知识 兄弟 Blog StringUti…...
工业蒸汽量预测(速通一)
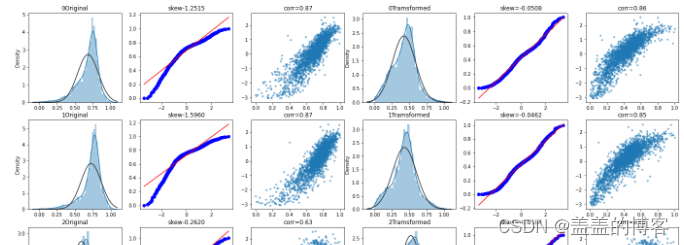
工业蒸汽量预测(一) 赛题理解1、评估指标2、赛题模型3、解题思路 理论知识1、变量识别2、变量分析3、缺失值处理4、异常值处理5、变量转换6、新变量生成 数据探索1、导包2、读取数据3、查看数据4、可视化数据分布4.1箱型图4.2获取异常数据并画图4.3直方图…...

机器学习的主要内容
分类任务 回归任务 有一些算法只能解决回归问题有一些算法只能解决分类问题有一些算法的思路既能解决回归问题,又能解决分类问题 一些情况下, 回归任务可以转化为分类任务, 比如我们预测学生的成绩,然后根据学生的成绩划分为A类、…...
)
华为OD机试真题-分积木-2023年OD统一考试(B卷)
题目描述: Solo和koko是两兄弟,妈妈给了他们一大堆积木,每块积木上都有自己的重量。现在他们想要将这些积木分成两堆。哥哥Solo负责分配,弟弟koko要求两个人获得的积木总重量“相等”(根据Koko的逻辑),个数可以不同,不然就会哭,但koko只会先将两个数转成二进制再进行加…...

SpringBoot自动装配原理及分析
一、什么是自动装配 在使用SpringBoot的时候,会自动将Bean装配到IoC容器中。例如我们在使用Redis数据库的时候,会引入依赖spring-boot-starter-data-redis。在引入这个依赖后,服务初始化的时候,会将操作Redis需要的组件注入到IoC…...
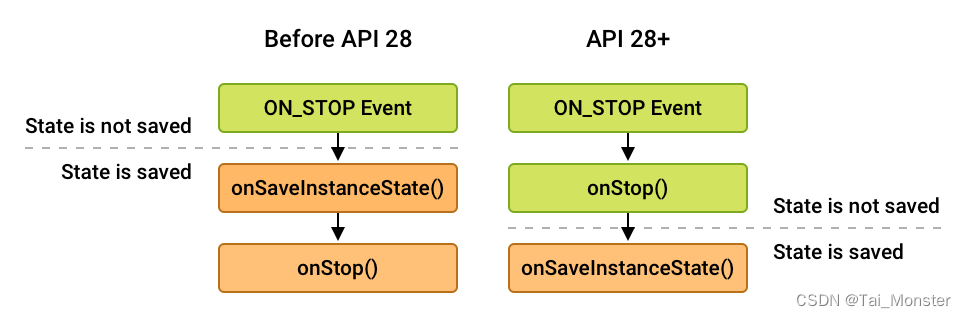
Android开发笔记 :理解Fragment
Android开发笔记:理解Fragment 导言 本篇文章产生的原因很简单,就是我在了解Android Jetpack中的Lifecycle框架时发现Lifecycle具体时间和状态的更新都是由一个名为ReportFragment的Fragment来跟踪的,为了更好的了解Fragment是如何追踪Activ…...

std::chrono获取当前秒级/毫秒级/微秒级/纳秒级时间戳
当前时间戳获取方法 先使用std::chrono获取当前系统时间,然后将当前系统时间转换为纪元时间std::time_t类型,之后使用std::localtime对std::time_t类型转换为本地时间结构体std::tm类型,最后使用strftime对时间进行格式化输出。 其中std::t…...

sh文件介绍及linux下执行
Shell脚本是一种用于自动化任务和系统管理的脚本语言。它允许用户通过命令行界面执行一系列命令,从而简化了重复性任务的处理过程。 以下是关于Shell脚本的一些基本概念: 1. Shell脚本通常以“.sh”扩展名保存,例如“script.sh”。 2. Shell…...

js-cookie使用 js深度克隆(判断引用类型是数组还是对象的方法)
cookie和深度拷贝的使用 1、js-cookie使用2、js深度克隆 1、js-cookie使用 前端的本地存储分为 localstorage、sesstionstorage、cookie 但是咱们有时候需要做7天免登录的需求时,选择 cookie 作为前端的本地存储是在合适不过的了 直接操作 cookie 可以, …...

[Pytorch]语义分割任务分类的实现
文章目录 [Pytorch]语义分割任务分类的实现 [Pytorch]语义分割任务分类的实现 假如我们定义了一个网络用于语义分割任务,这个网络简称为model() 语义分割任务要做的是: 对于一个图片输入input,大小为(B,C,…...
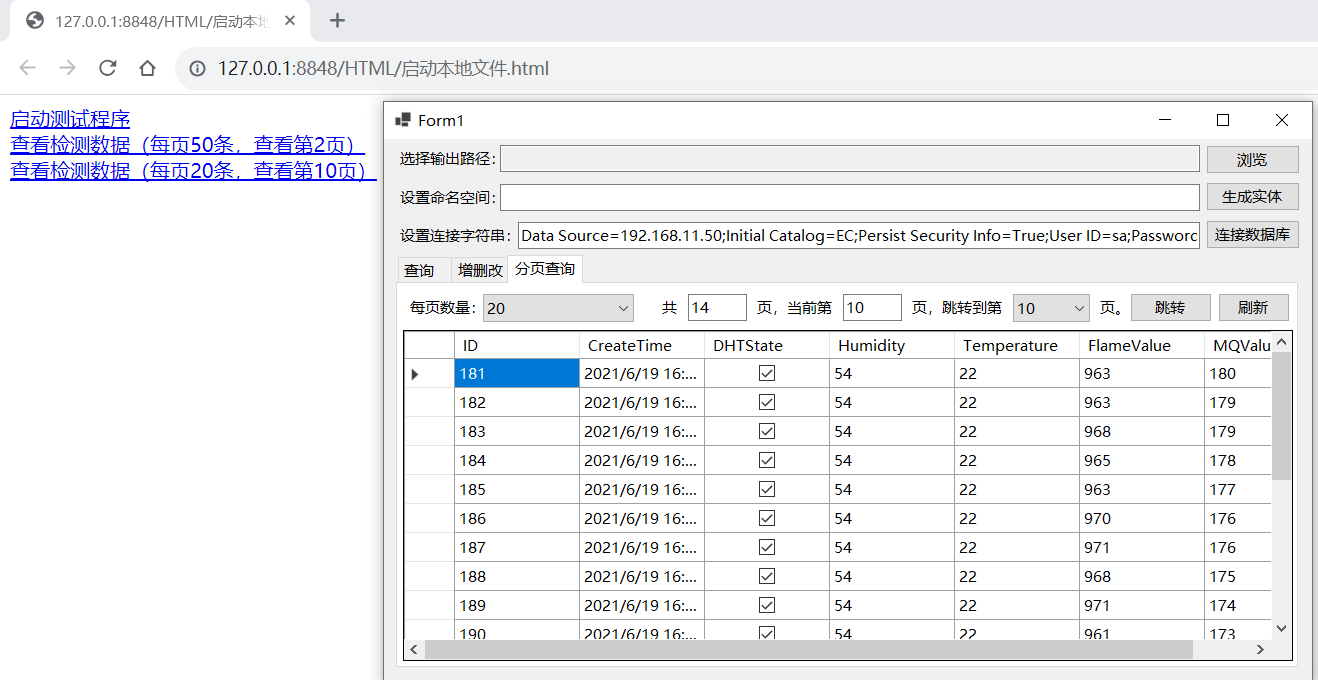
测试网页调用本地可执行程序(续:带参数调用)
前篇文章介绍了网页调用本地可执行程序的方式,通过在注册表中注册命令,然后在网页中调用命令启动本地程序。如果需要传递参数,则需要在注册表命令中的command项中设置如下形式的值。 "XXXXXX\XXXXXXX.exe" "%1"&emsp…...

Carla自动驾驶模拟器安装和使用
Carla自动驾驶模拟器安装和使用 1 安装 ubuntu20.04安装carla0.9.11版本 步骤1:打开下面链接,点击第一个[Ubuntu] CARLA_0.9.11.tar.gz carla-0.9.11源码下载 步骤2:下载完解压到/opt目录下 我的话是先在下载目录上提取解压,然…...
【每日一题】1539. 第 k 个缺失的正整数
1539. 第 k 个缺失的正整数 - 力扣(LeetCode) 给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。 请你找到这个数组里第 k 个缺失的正整数。 示例 1: 输入:arr [2,3,4,7,11], k 5 输出:9 解释:缺失…...

AI-Chat,一款集全网ai功能的应用(附下载链接)
AI-Chat是一款综合性的聊天机器人,集成了多种先进的模型和功能。它采用了GPT4.0、联网版GPT和清华模型等多种模型,使得其具备更强大的语言处理能力。同时,AI-Chat还融合了AI绘画模型,例如Stable Diffusion绘画、文生图、图生图、艺…...

3、靶场——Pinkys-Place v3(3)
文章目录 一、获取flag41.1 关于SUID提权1.2 通过端口转发获取setuid文件1.3 运行pinksecd文件1.4 利用nm对文件进行分析1.5 构建payload1.6 Fire 二、获取flag52.1 生成ssh公钥2.2 免密登录ssh2.3 以pinksecmanagement的身份进行信息收集2.4 测试程序/usr/local/bin/PSMCCLI2.…...
什么是 AirServer?Mac专用投屏工具AirServer 7 .27 for Mac中文破解版百度网盘下载
AirServer 7 .27 for Mac中文免费激活版是一款Mac专用投屏工具,能够通过本地网络将音频、照片、视频以及支持AirPlay功能的第三方App,从 iOS 设备无线传送到 Mac 电脑的屏幕上,把Mac变成一个AirPlay终端的实用工具。 目前最新的AirServer 7.2…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
