【机器学习】详解回归(Regression)
文章目录
- 是什么的问题
- 案例说明
是什么的问题
- 回归分析(Regression Analysis) 是研究自变量与因变量之间数量变化关系的一种分析方法,它主要是通过因变量Y与影响它的自变量 X i ( i 1 , 2 , 3 … ) X_i(i1,2,3…) Xi(i1,2,3…)之间的回归模型,衡量自变量 X i X_i Xi对因变量Y的影响能力的,进而可以用来预测因变量Y的发展趋势。
- 损失函数(Cost Function/Lost Function) 用于估计模型的预测值和真实值之间的不一致程度,损失函数越小代表模型预测结果与真实值越相近。
定义线性回归的损失函数,可采用最小二乘法,通过最小化误差的平方和寻找数据的最佳函数匹配。
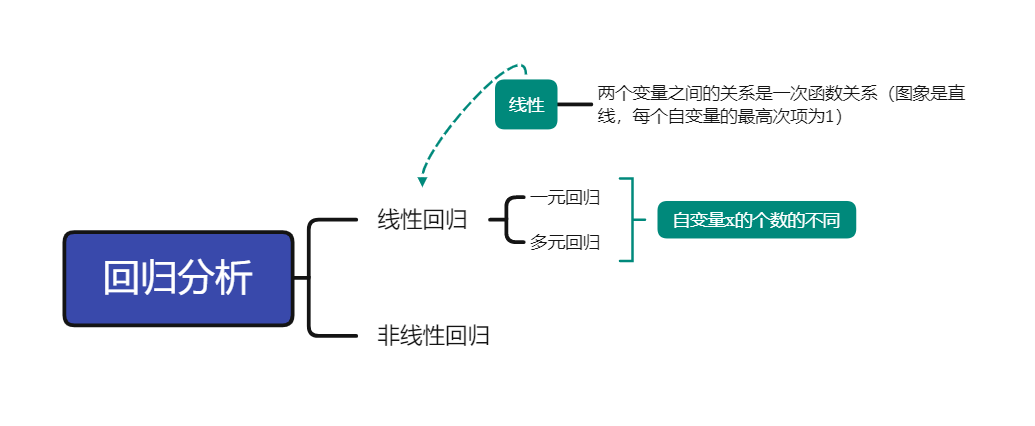
单个样本(example)的误差函数:
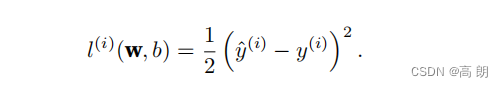
总体n的误差函数:
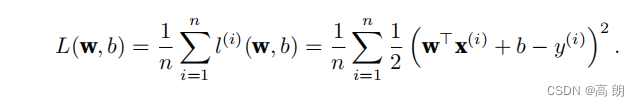 线性回归模型的函数: y ^ = w 1 x 1 + w 2 x 2 + . . . + w d x d + b = W T X + b \hat{y}=w_1x_1+w_2x_2+...+w_dx_d+b=W^TX+b y^=w1x1+w2x2+...+wdxd+b=WTX+b
线性回归模型的函数: y ^ = w 1 x 1 + w 2 x 2 + . . . + w d x d + b = W T X + b \hat{y}=w_1x_1+w_2x_2+...+w_dx_d+b=W^TX+b y^=w1x1+w2x2+...+wdxd+b=WTX+b
在训练模型时,我们希望寻找⼀组参数(w∗, b∗),这组参数能最⼩化在所有训练样本上的总损失。
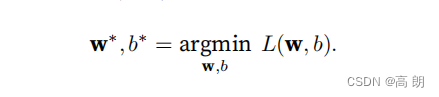
- 如何找到最优的w,b来优化我们的模型?
用数学的方法就是把w,b看成未知变量,分别对其求偏导。
L ( w , b ) = ∑ i = 1 n ( W T X + b i − y i ) 2 L(w,b)=\sum_{i=1}^{n} (W^TX+bi-y_i)^2 L(w,b)=i=1∑n(WTX+bi−yi)2
因为我们求L最小时,w和b的值,去掉前面的非0正系数不影响。
求参数w:
 求参数b:同上
求参数b:同上

案例说明
问题:预测宝可梦升级后的cp值
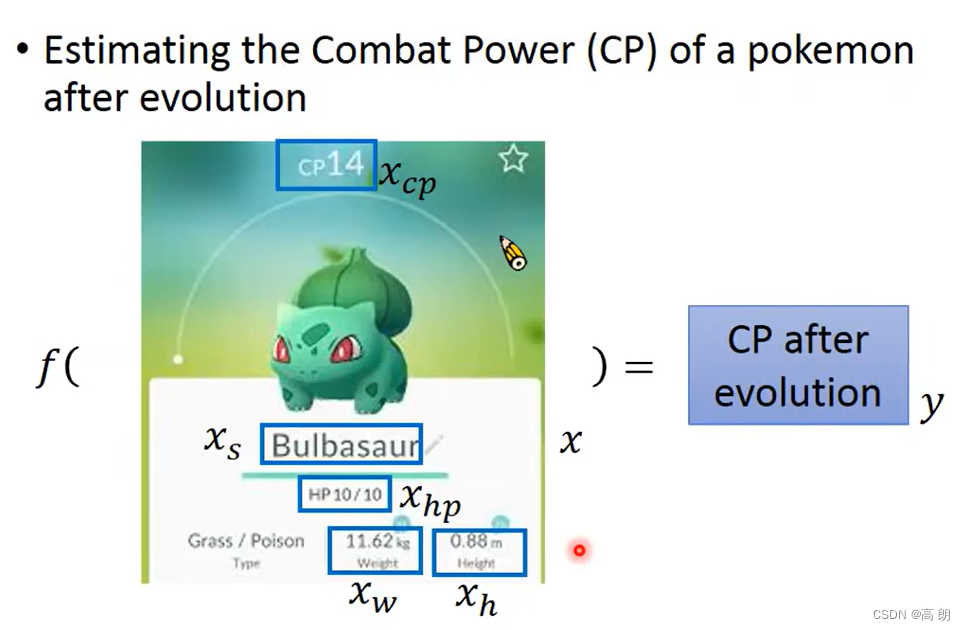 Step1: model (设计网络模型)define a set of function
Step1: model (设计网络模型)define a set of function
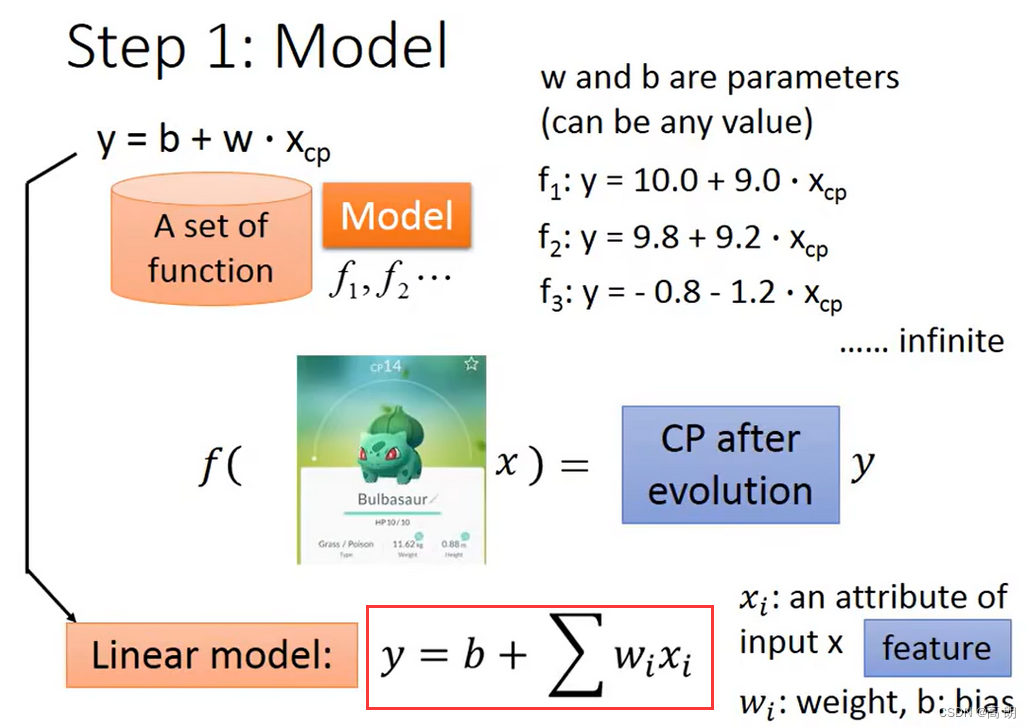
b是bias(偏置), w i w_i wi是weight(权重), X c p X_{cp} Xcp是我们输入的cp值
线性模型: y = b + w 1 x 1 + w 2 x 2 + . . . + w i x i y = b + w_1x_1 + w_2x_2 + ... + w_ix_i y=b+w1x1+w2x2+...+wixi
b和w的值是有很多个的,所以有a set of function,需要通过这个train data去找到这个最合适的function。
step 2: Goodness of function(函数的好坏)
 通过第一另外一个function:Loss来判断上面的function的好坏
通过第一另外一个function:Loss来判断上面的function的好坏
 Loss function 是去衡量y的好坏,去判断我们找到的w,b的好坏
Loss function 是去衡量y的好坏,去判断我们找到的w,b的好坏
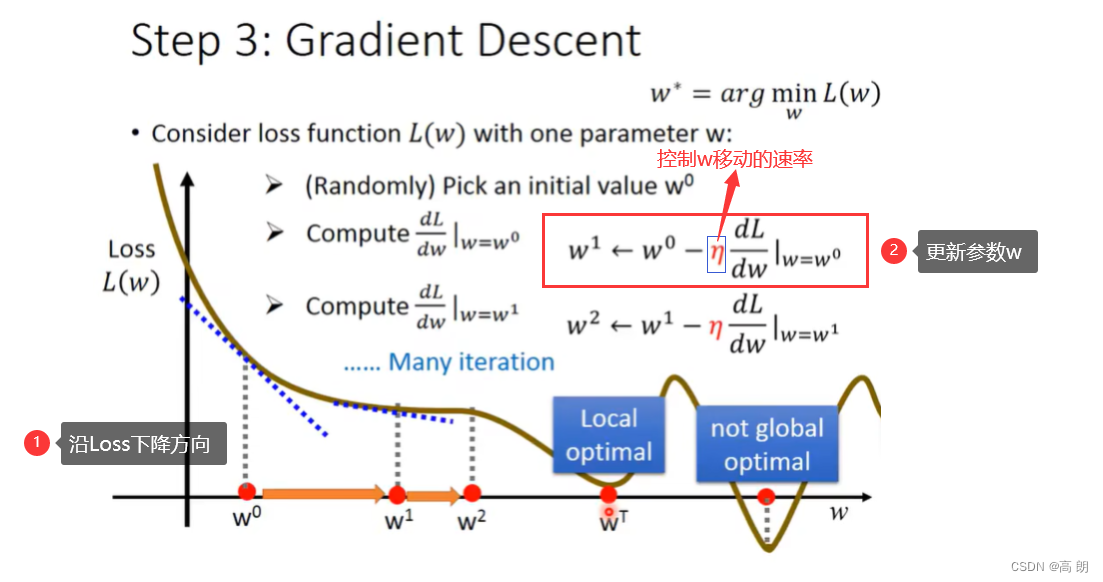
step 3: Best Funciton(Gradient Descent)
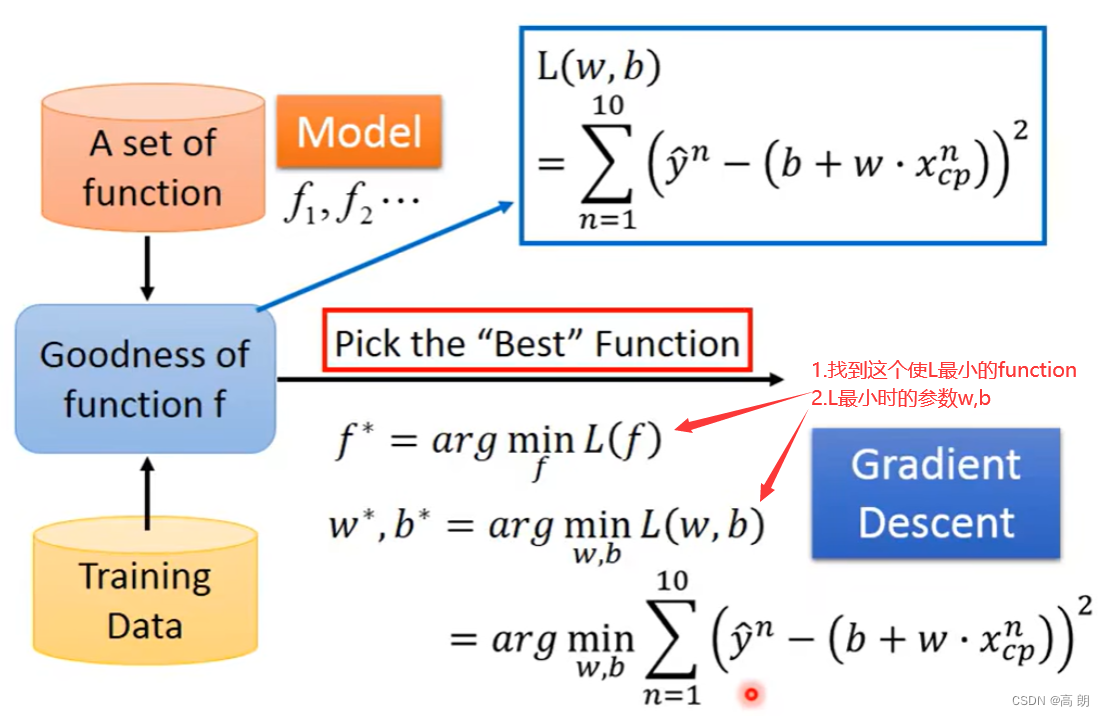 很显然,就是求L分别对w,b的偏导,通过梯度下降的方式来找到最小的L。
很显然,就是求L分别对w,b的偏导,通过梯度下降的方式来找到最小的L。
单个参数的考虑:
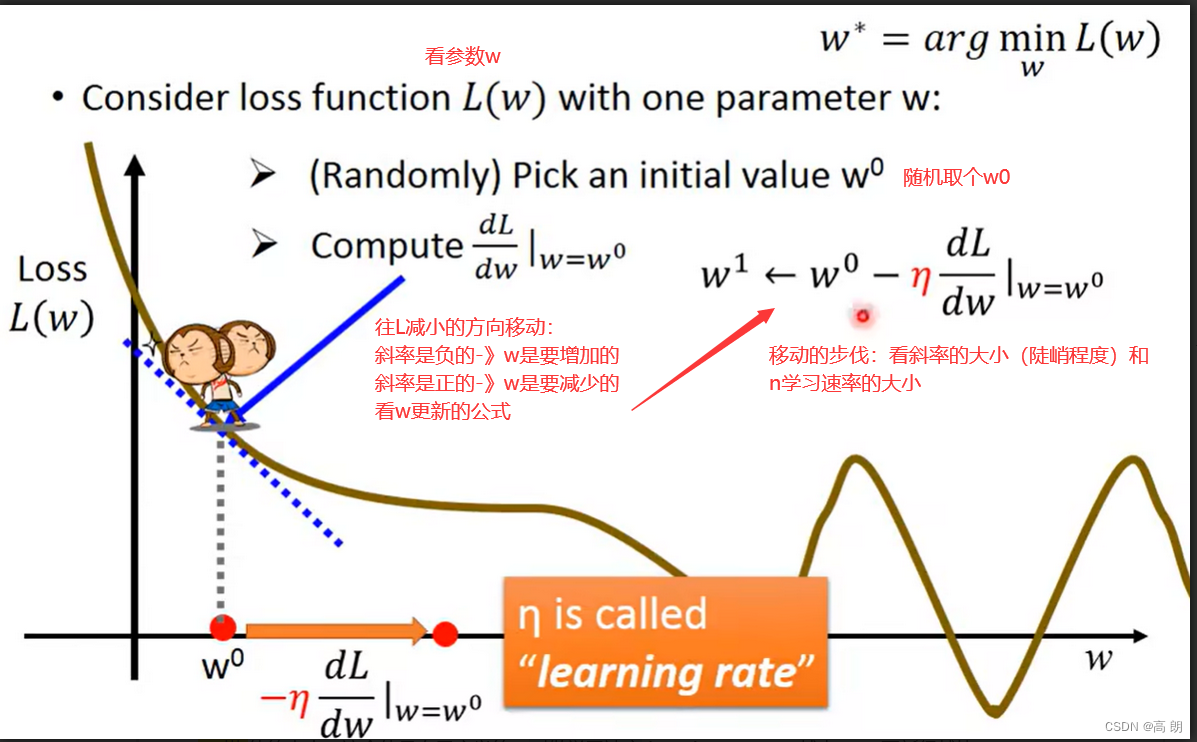 通过不断更新,使得L最小,会到达一个局部最优(local optimal),斜率为0或接近于0,这个时候就无法再更新w了,所以是不能找到全局最优(global optimal)。
通过不断更新,使得L最小,会到达一个局部最优(local optimal),斜率为0或接近于0,这个时候就无法再更新w了,所以是不能找到全局最优(global optimal)。
俩个参数的考虑:

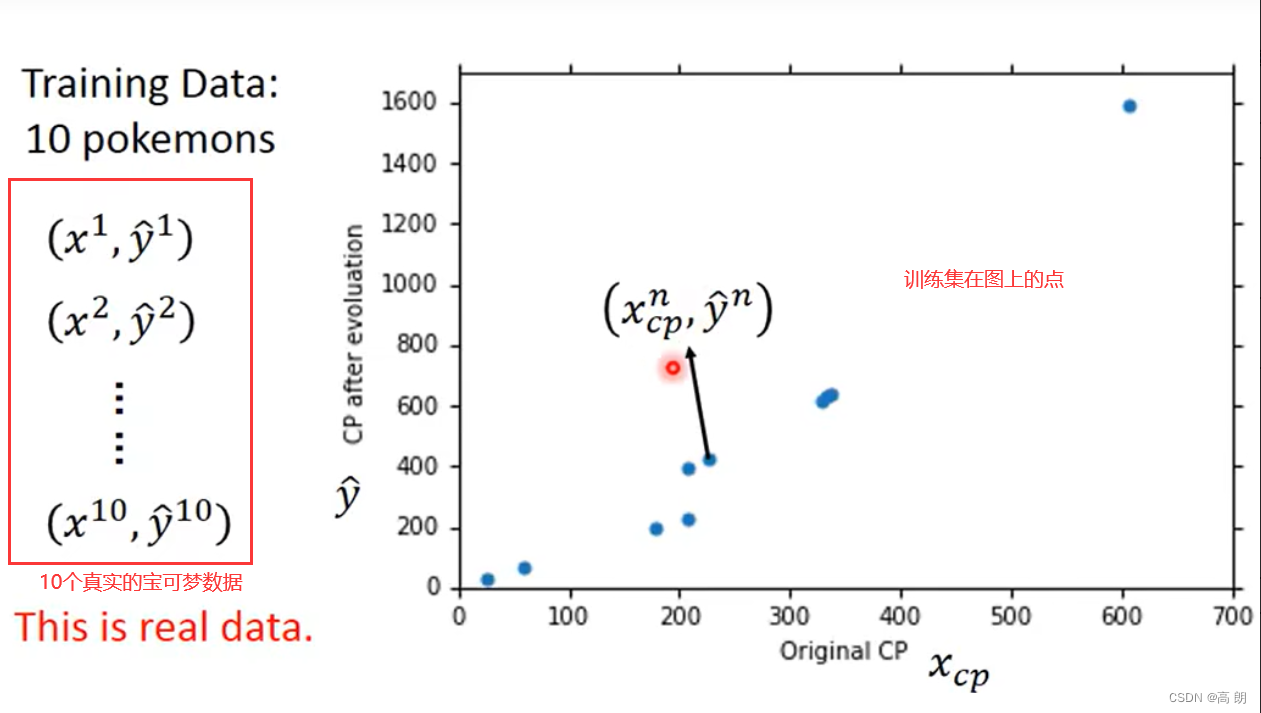
 最后,通过上面的10个宝可梦的数据,得到参数b,w,然后进行测试:
最后,通过上面的10个宝可梦的数据,得到参数b,w,然后进行测试:
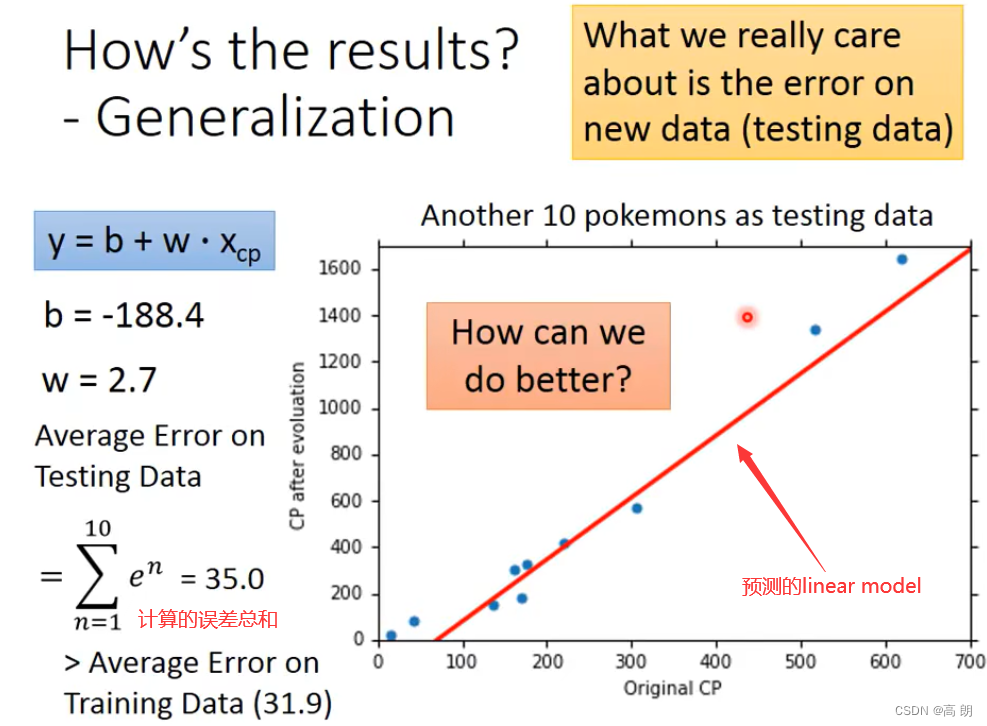
怎样获得更好的结果呢?怎样让预测更加准确呢?
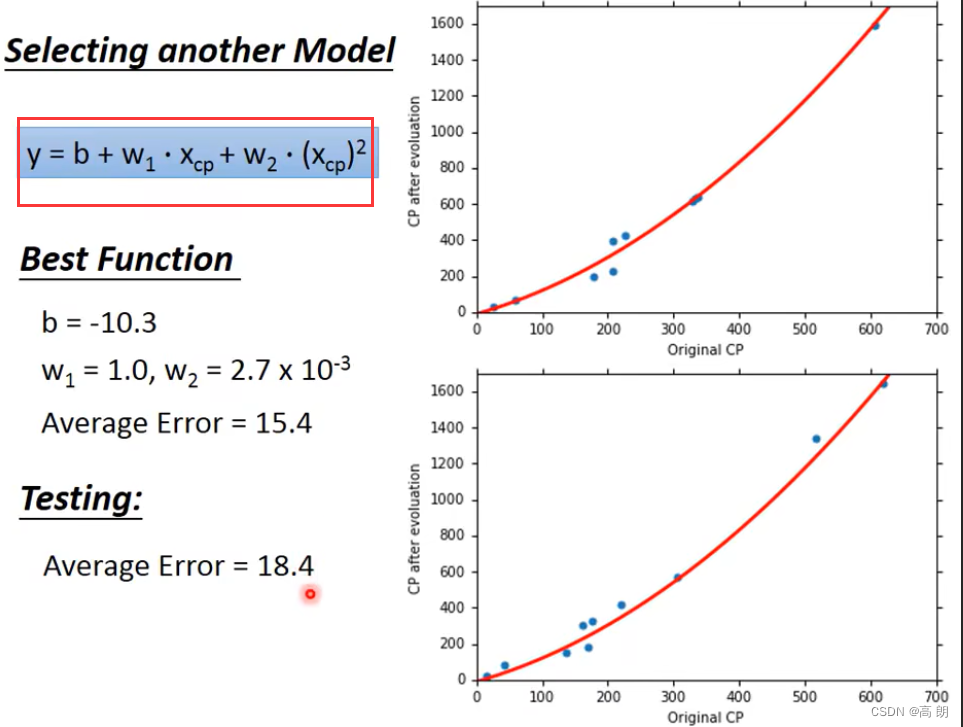
其实就是需要改变模型:(这里改成二次式)
多项式回归(Polynomial Regression), 多项式回归与线性回归的概念相同,只是它使用的是曲线而不是直线(线性回归使用的是直线)。多项式回归学习更多的参数来绘制非线性回归曲线。对于不能用直线概括的数据,它是有益的。多项式回归是将自变量x与因变量y之间的关系建模为n次多项式的一种线性回归形式。多项式回归拟合了x值与y相应条件均值之间的非线性关系,记为E(y |x)。
或者说还想更好,那么可以尝试从二次转化为三次
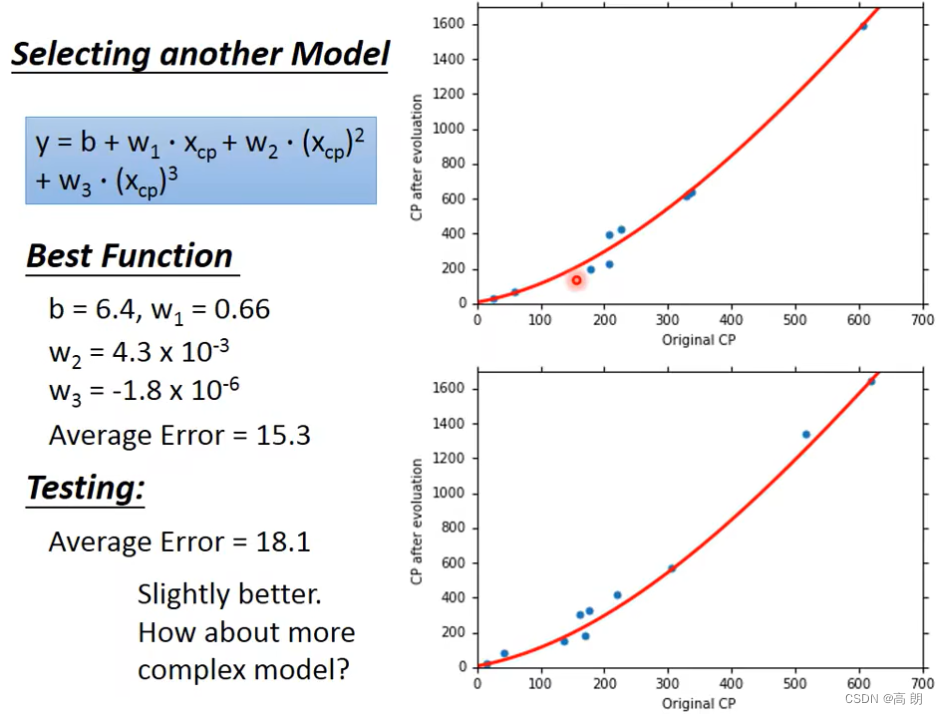 四次:
四次:
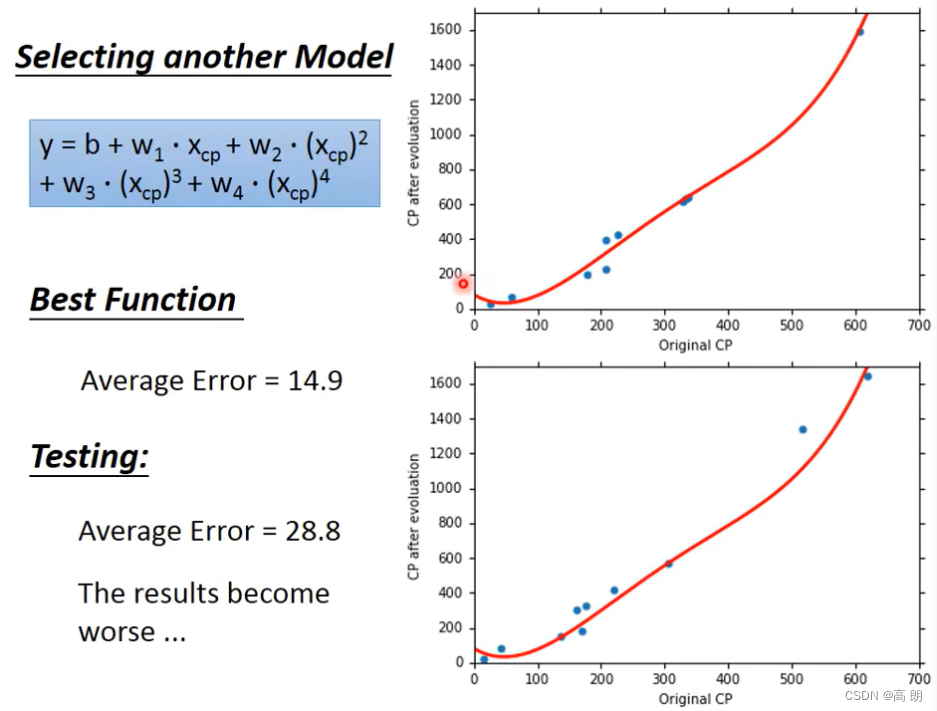 从这里开始,虽然换成了更复杂的Mode。但是测试的结果,average error变大了,results become worse…
从这里开始,虽然换成了更复杂的Mode。但是测试的结果,average error变大了,results become worse…
五次:
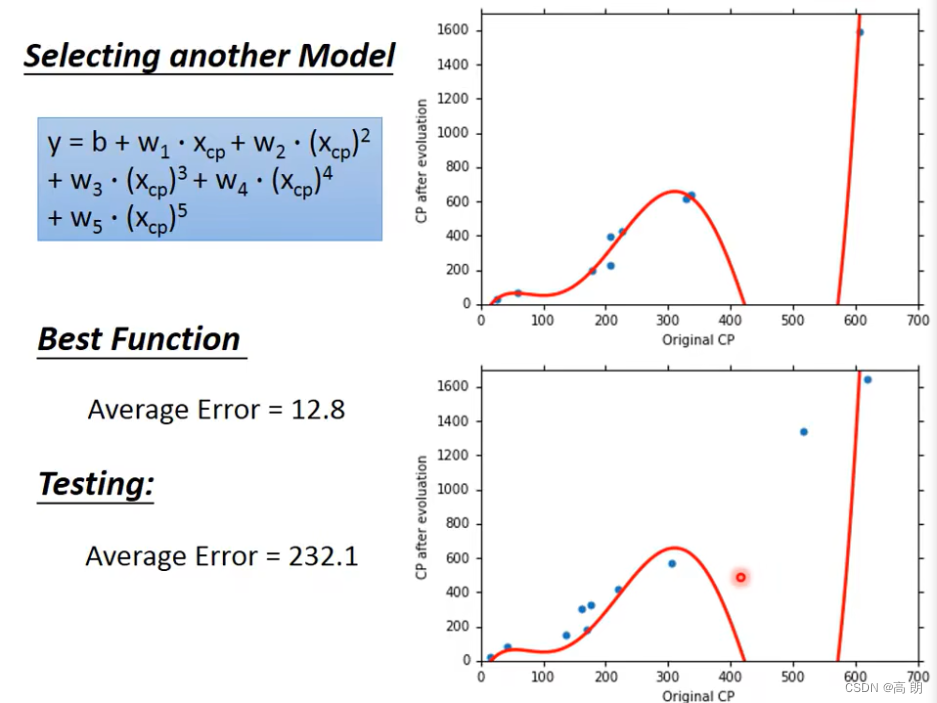 综上:
综上:
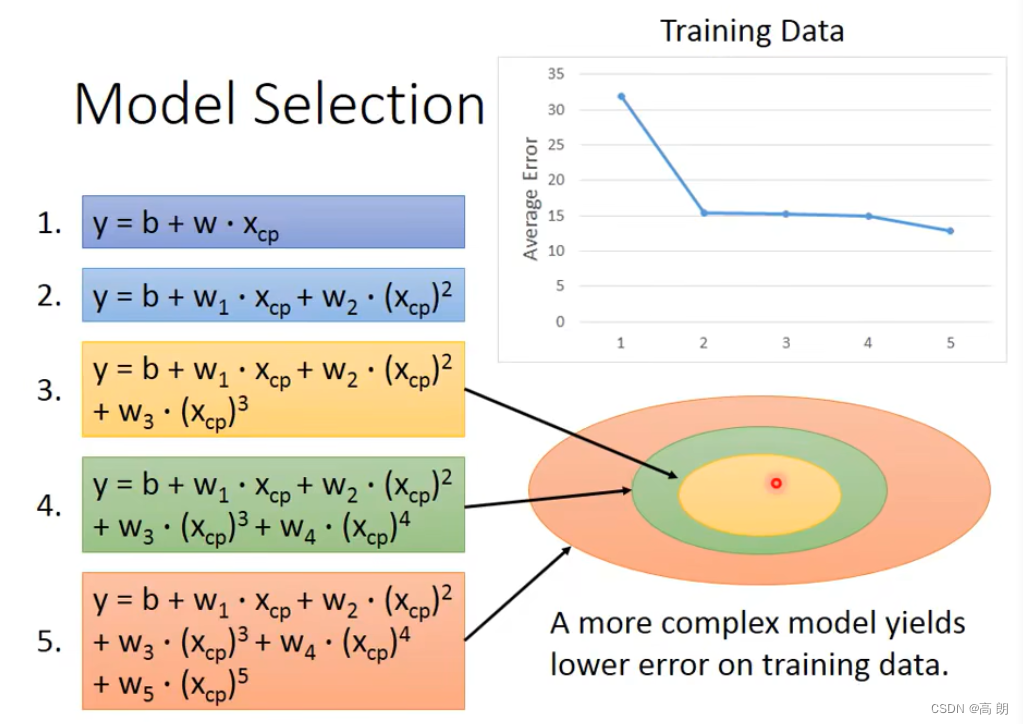 模型model越复杂,包含的train data越多,在训练集上的误差越小。
模型model越复杂,包含的train data越多,在训练集上的误差越小。
 但是更加复杂的模型不一定能在测试数据中带来更好的表现。会出现【过拟合】,所以,我们要选择一个最适合我们的model而不是最复杂的model。因为,可能会导致过拟合。上图中最好的model是三次式的。
但是更加复杂的模型不一定能在测试数据中带来更好的表现。会出现【过拟合】,所以,我们要选择一个最适合我们的model而不是最复杂的model。因为,可能会导致过拟合。上图中最好的model是三次式的。
当增加更多的宝可梦数据时,会发现不仅仅只有一个cp值的影响,还有物种的影响,所以需要重新设计我们的model

重新设计的model,增加了物种因素:
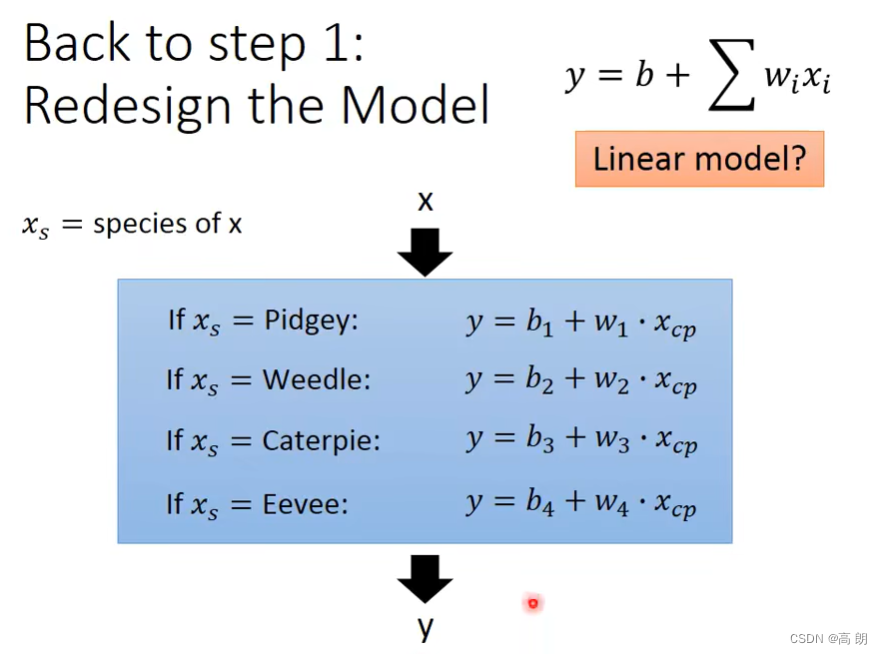 结果:
结果:
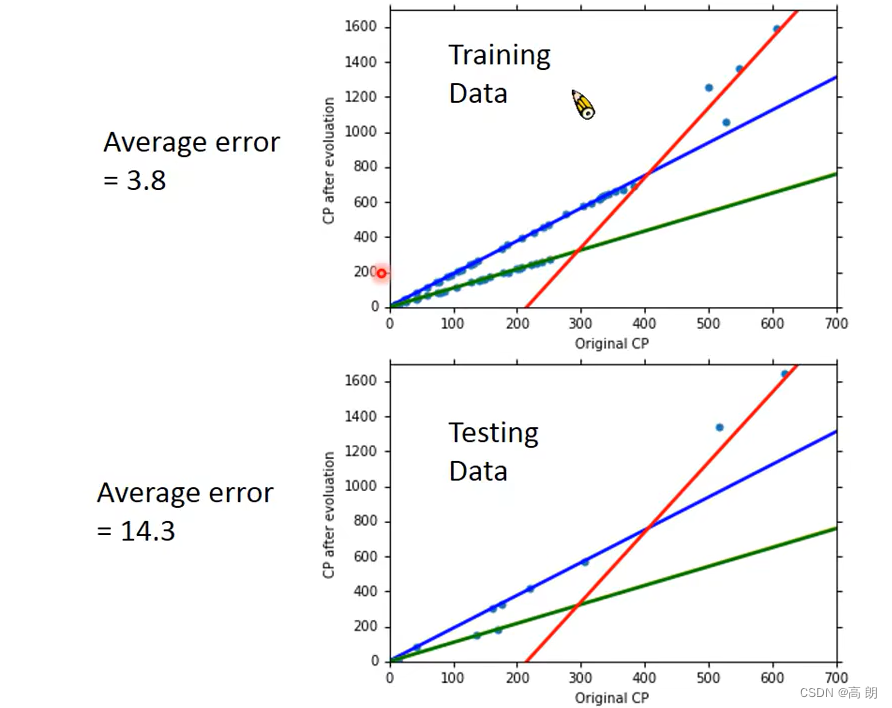 上分类后得到的linear model,结果明显比原来的没有分类的好太多了。尝试增加更多因素,修改model:(量,高度,HP值)
上分类后得到的linear model,结果明显比原来的没有分类的好太多了。尝试增加更多因素,修改model:(量,高度,HP值)
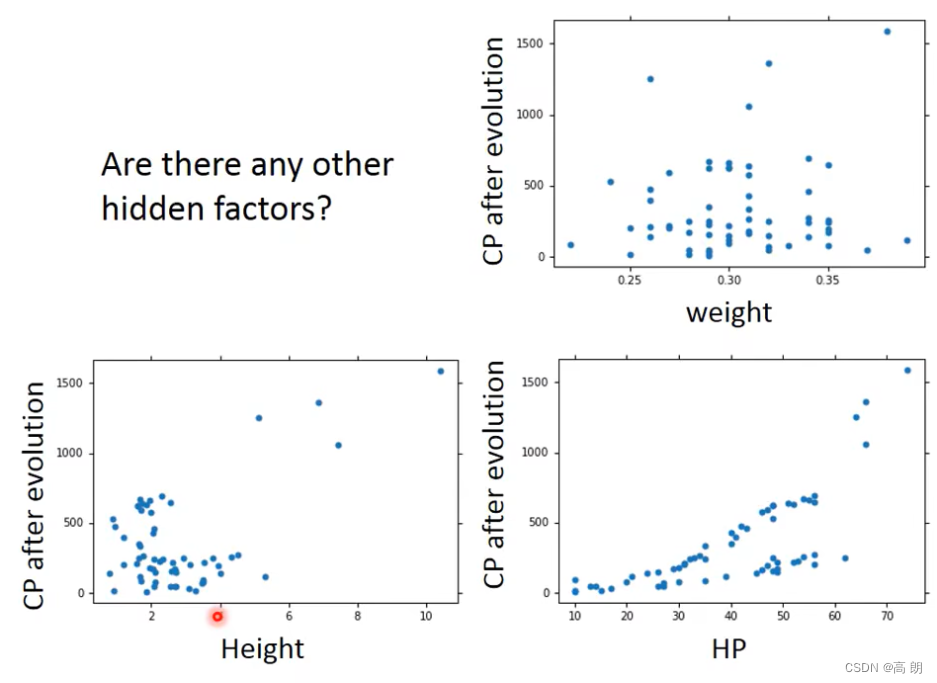 重新设计的model:
重新设计的model:
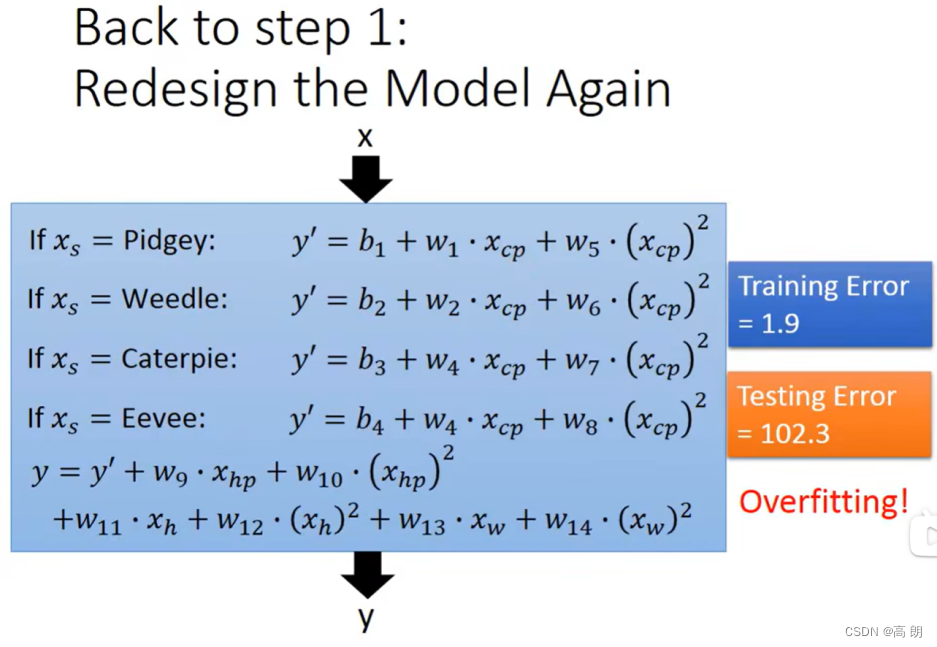 最终结果训练误差小了很多,但是测试误差太大了,过拟合了。遇到这个情况需要引出一个新的概念:正则化(Regularization)
最终结果训练误差小了很多,但是测试误差太大了,过拟合了。遇到这个情况需要引出一个新的概念:正则化(Regularization)
Back to step 2: Regularization(正则化) 正则化就是说给需要训练的目标函数加上一些规则(限制),让我们的函数尽量平缓,别过于膨胀,我们在梯度函数中加上 w e i g h t 2 weight^2 weight2这一项,这样就可以很好控制weight的大小。
 重新训练的结果:
重新训练的结果:
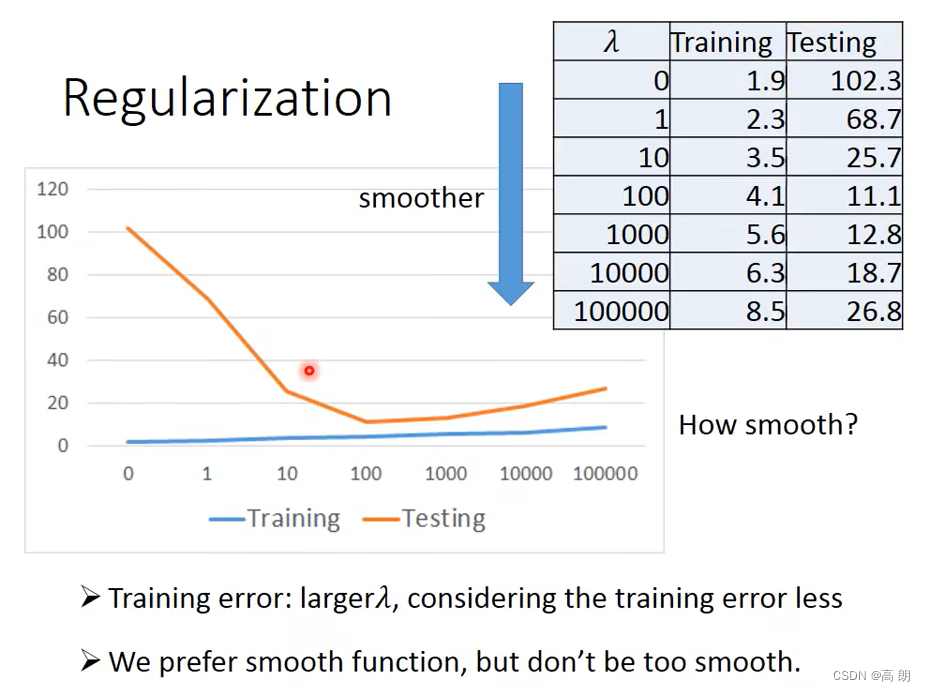 当λ=100时,达到这个模型的最佳测试Loss
当λ=100时,达到这个模型的最佳测试Loss
相关文章:

【机器学习】详解回归(Regression)
文章目录 是什么的问题案例说明 是什么的问题 回归分析(Regression Analysis) 是研究自变量与因变量之间数量变化关系的一种分析方法,它主要是通过因变量Y与影响它的自变量 X i ( i 1 , 2 , 3 … ) X_i(i1…...
mac 配置 httpd nginx php-fpm 详细记录 已解决
在日常mac电脑 开发php项目一直是 httpd 方式 运行,由于有 多版本 运行的需求,docker不想用,索性用 php-fpm进行 功能处理。上次配置 是好的,但是感觉马马虎虎,这次 配置底朝天。因为配置服务器,几乎也都是…...

Angular 项目升级需要注意什么?
升级Angular项目是一个重要的任务,因为它可以帮助你获得新的功能、性能改进和安全性增强。然而,Angular的版本升级可能会涉及到一些潜在的问题和挑战。以下是升级Angular项目时需要注意的一些重要事项: 备份项目:在升级之前&…...

开发高性能知识付费平台:关键技术策略
引言 在构建知识付费平台时,高性能是确保用户满意度和平台成功的关键因素之一。本文将探讨一些关键的技术策略,帮助开发者打造高性能的知识付费平台。 1. 前端性能优化 使用CDN加速资源加载 使用内容分发网络(CDN)来托管和加…...

python图像匹配:如何使用Python进行图像匹配
Python图像匹配是指使用Python编写的程序来进行图像匹配。它可以在两幅图像之间找到相似的部分,从而实现图像检索、图像比较、图像拼接等功能。 Python图像匹配是指使用Python编写的程序来进行图像匹配。它可以在两幅图像之间找到相似的部分,从而实现图…...
R语言绘制PCA双标图、碎石图、变量载荷图和变量贡献图
1、原论文数据双标图 代码: setwd("D:/Desktop/0000/R") #更改路径#导入数据 df <- read.table("Input data.csv", header T, sep ",")# ----------------------------------- #所需的包: packages <- c("ggplot2&quo…...
)
Jolokia 笔记 (Kafka/start/stop)
目录 1. Jolokia 笔记 (Kafka/start/stop) 1. Jolokia 笔记 (Kafka/start/stop) java -javaagent:agent.jarport8778,hostlocalhostJolokia 是作为 Kafka 的 Java agent, 基于 HTTP 协议提供了一个使用 JSON 作为数据格式的外部接口, 提供给 DataKit 使用。 Kafka 启动时, 先配…...
Qt5开发及实例V2.0-第十九章-Qt.QML编程基础
Qt5开发及实例V2.0-第十九章-Qt.QML编程基础 第19章 QML编程基础19.1 QML概述19.1.1 第一个QML程序19.1.2 QML文档构成19.1.3 QML基本语法 19.2 QML可视元素19.2.1 Rectangle(矩形)元素19.2.2 Image(图像)元素19.2.3 Text…...

固定开发板的ifconfig的IP地址
背景 由于我是使用vsocode的ssh插件远程连接我的开发板, 所以我每次开机就要重新连上屏幕看一下这个ifconfig的ip地址然后更改我的ssh config文件 这里提供一个使用nmcli设置静态IP的方法 请确保使用你的实际连接名称替换Wi-Fi connection 1 使用nmcli设置静态IP相对直接&a…...

停车场系统源码
源码下载地址(小程序开源地址):停车场系统小程序,新能源电动车充电系统,智慧社区物业人脸门禁小程序: 【涵盖内容】:城市智慧停车系统,汽车新能源充电,两轮电动车充电,物…...

R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例...
原文链接:http://tecdat.cn/?p23236 在频率学派中,观察样本是随机的,而参数是固定的、未知的数量(点击文末“阅读原文”获取完整代码数据)。 相关视频 什么是频率学派? 概率被解释为一个随机过程的许多观测…...
若依前后端分离如何解决匿名注解启动报错?
SpringBoot2.6.0默认是ant_path_matcher解析方式,但是2.6.0之后默认是path_pattern_parser解析方式。 所以导致读取注解类方法需要对应的调整,当前若依项目默认版本是2.5.x,如果使用大于2.6.x,需要将info.getPatternsCondition().getPatterns()修改为info.getPathPatterns…...

Spring面试题4:面试官:说一说Spring由哪些模块组成?说一说JDBC和DAO之间的联系和区别?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:说一说Spring由哪些模块组成? Spring是一个开源的Java框架,由多个模块组成,每个模块都提供不同的功能和特性。下面是Spring框架的主要模块: S…...
【再识C进阶3(上)】详细地认识字符串函数、进行模拟字符串函数以及拓展内容
小编在写这篇博客时,经过了九一八,回想起了祖国曾经的伤疤,勿忘国耻,振兴中华!加油,逐梦少年! 前言 💓作者简介: 加油,旭杏,目前大二,…...

docker启动mysql8目录挂载改动
5.7版本: 拉取mysql镜像 docker pull mysql:5.7启动 docker run -p 3306:3306 --name mysql5 \ -v /Users/zhaosichun/data/dockerData/log:/var/log/mysql \ -v /Users/zhaosichun/data/dockerData/data:/var/lib/mysql \ -v /Users/zhaosichun/data/dockerData…...
CHATGPT中国免费网页版有哪些-CHATGPT中文版网页
CHATGPT中国免费网页版,一个强大的人工智能聊天机器人。如果你曾经感到困惑、寻求答案,或者需要一些灵感,那么CHATGPT国内网页版可能会成为你的好朋友。 CHATGPT国内免费网页版:你的多面“好朋友” 随着人工智能技术的不断发展&a…...

docker network create命令
docker network create命令用于创建一个新的网络连接。 DRIVER接受内置网络驱动程序的桥接或覆盖。如果安装了第三方或自己的自定义网络驱动程序,则可以在此处指定DRIVER。 如果不指定--driver选项,该命令将为您自动创建一个桥接网络。 当安装Docker Eng…...
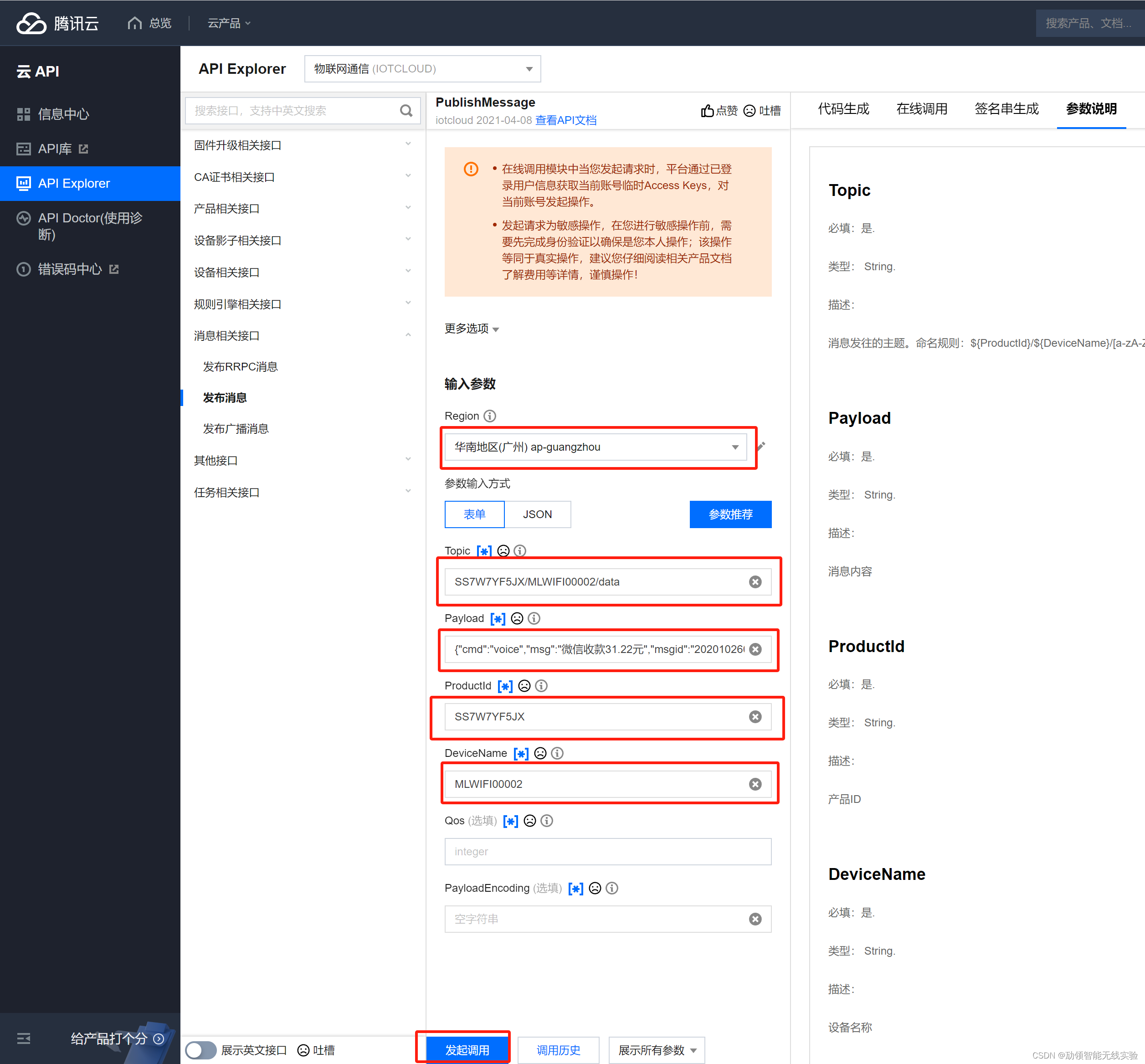
4G版本云音响设置教程腾讯云平台版本
文章目录 4G本云音响设置教程介绍一、申请设备三元素1.腾讯云物联网平台2.创建产品3.设置产品参数4.添加设备5.获取三元素 二、设置设备三元素1.打开MQTTConfigTools2.计算MQTT参数3.使用USB连接设备4.设置参数 三、腾讯云物联网套件协议使用说明1.推送协议信息2.topic规则说明…...
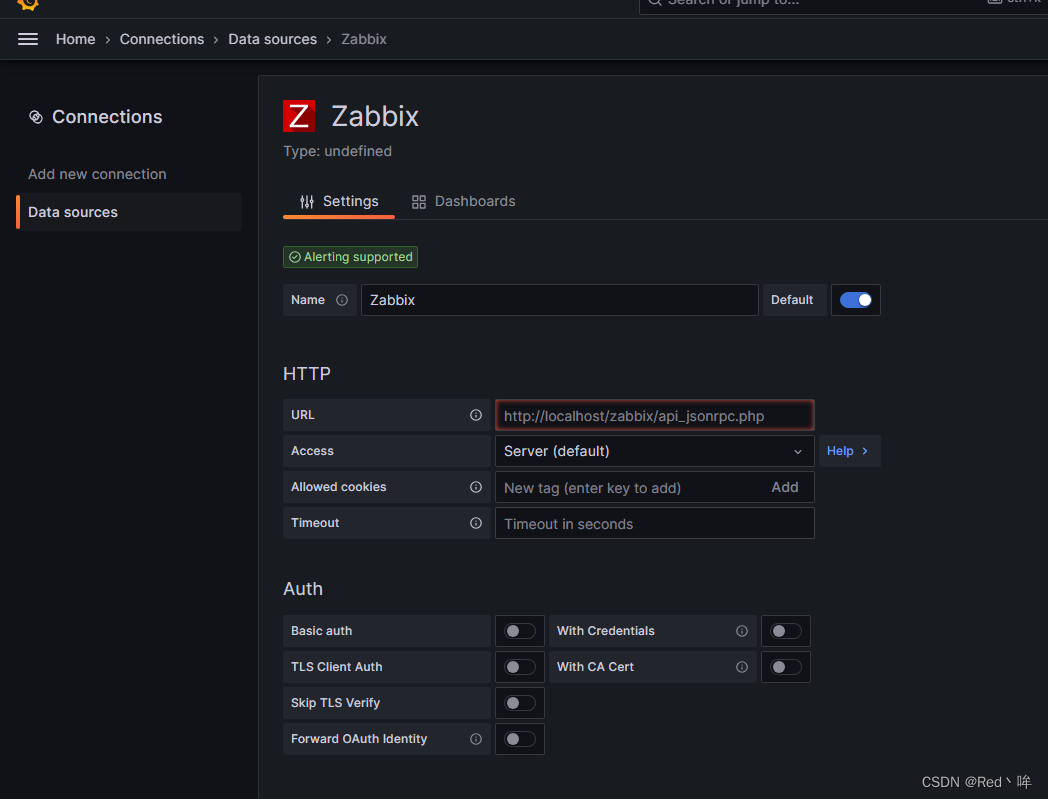
Grafana离线安装部署以及插件安装
Grafana是一个可视化面板(Dashboard),有着非常漂亮的图表和布局展示,功能齐全的度量仪表盘和图形编辑器,支持Graphite、zabbix、InfluxDB、Prometheus和OpenTSDB作为数据源。Grafana主要特性:灵活丰富的图形…...

非独立随机变量的概率上界估计
目前的概率论或者随机变量书籍过分强调对独立随机变量的大数定律,中心极限定理,遗憾上界的估计。而对于非独立随机变量的研究很少,在《概率论的极限定理》中曾给出过一般随机变量求和的渐进分布簇的具体形式,然而形式却太过复杂。…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
