【机组】计算机系统组成课程笔记 第二章 计算机中的信息表示
2.1 无符号数和有符号数
2.1.1 无符号数
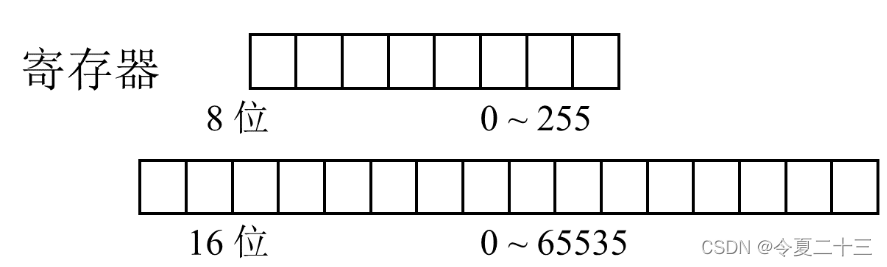
没有符号的数,其实就是非负数。在计算机中用字节码表示,目前最常用的是八位和十六位的。
2.1.2 有符号数
将正负符号数字化,0代表 + ,1代表 - ,并把代表符号的数字放在有效数字前,就组成了有符号数。
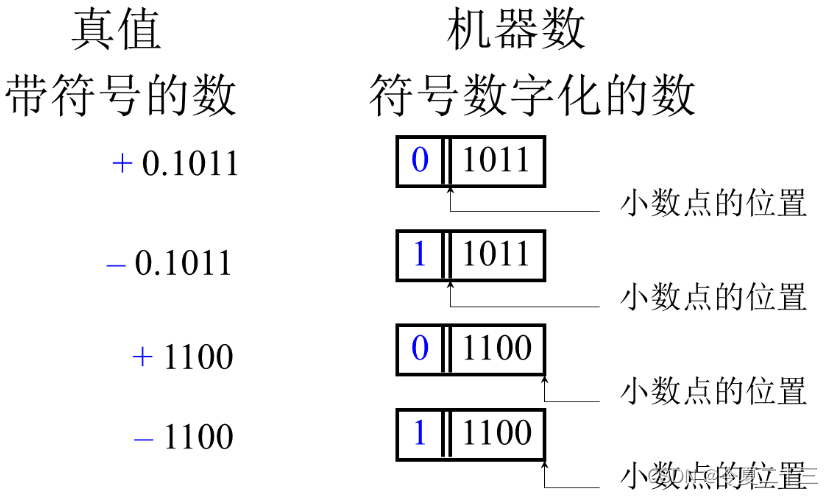
1. 机器数和真值
我们接下来要用到的真值都指的是带符号的二进制数。
机器数是相对于真值而言的,下面要讲的原码、补码、反码和移码都属于机器数。
2. 原码表示法
原码,顾名思义,是机器数最原本的表示方法,原码包括两个部分,符号位和数值位,符号位用0和1代表这个数的正负,数值位就是真值的绝对值。
为了区别用原码表示的整数和小数,整数的符号位和数值位用逗号隔开,小数的则用小数点隔开。
原码的优点:表示简单,易于和真值转换。
原码的定义 -- 整数

原码的定义 -- 小数
原码可以表示的小数范围在-1和1之间,其他带小数的数可以用整数+小数这样的组合来表示。

例题
注意,在由原码求真值的题目中,若结果为正,那也得加一个 + 号!


3. 补码表示法
补的概念
取模为12的时候,+2等价于-10,-4等价于+8,+3等价于+15等价于+27。
在上面的例子里,-10的补数为+2,-4的补数为+8。并且正数的补数是其本身。
由此可以知道,只要确定了模,就可以为任何一个负数找到与其对应的正数,也就是补数,这样就方便进行运算,在对含有负数的式子进行加法运算时,可以先将负数取补数,最后取模即可。
补的结论

补码的定义 -- 整数
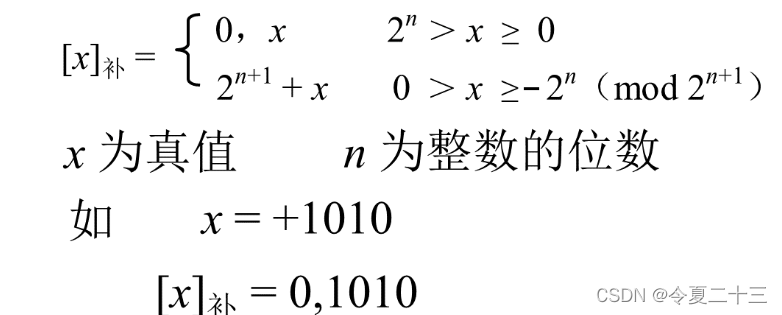
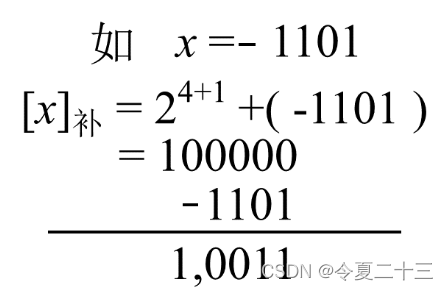
补码的定义 -- 小数
用补码表示负的小数时,因为符号位要为1,所以应该模2,也就是用2减去真值,这样得到的结果里,符号位一定为1,数值位即为真值的补数。
要注意,2也得用二进制来表示!
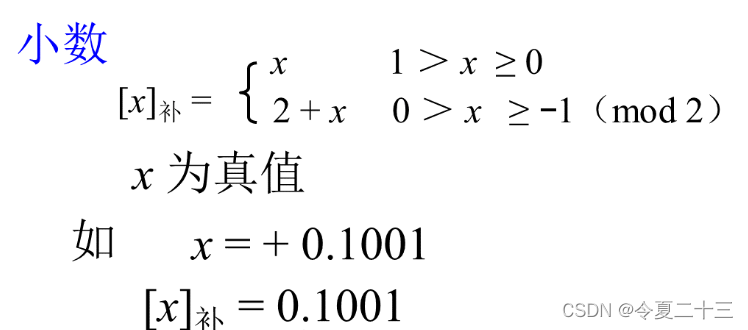

变形补码 -- 双符号位补码



求补码的快捷方式
对正数来说,补码就是符号位加上真值本身,简单易求;
对负数来说,求补码则有快捷方式:

总而言之,就是符号位不变,数值位取反,末尾加一。
4. 反码表示法
反码通常是基于上面原码与补码转换的快捷方式,所需要的中间过渡。
由于正数不需要快捷方式,所以反码还是和原码补码一样,只有符号位和真值不同。
只有负数需要将全体数值位转换为相反的数。
反码的定义 -- 整数

反码的定义 -- 小数
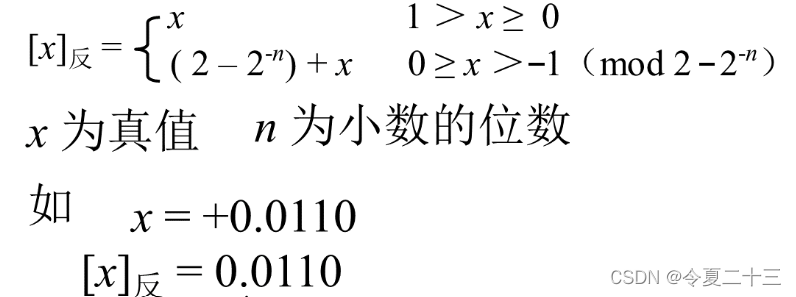

例题


5. 移码表示法
用原码和补码时很难一眼比出两个数的大小,这时候就需要使用移码了。
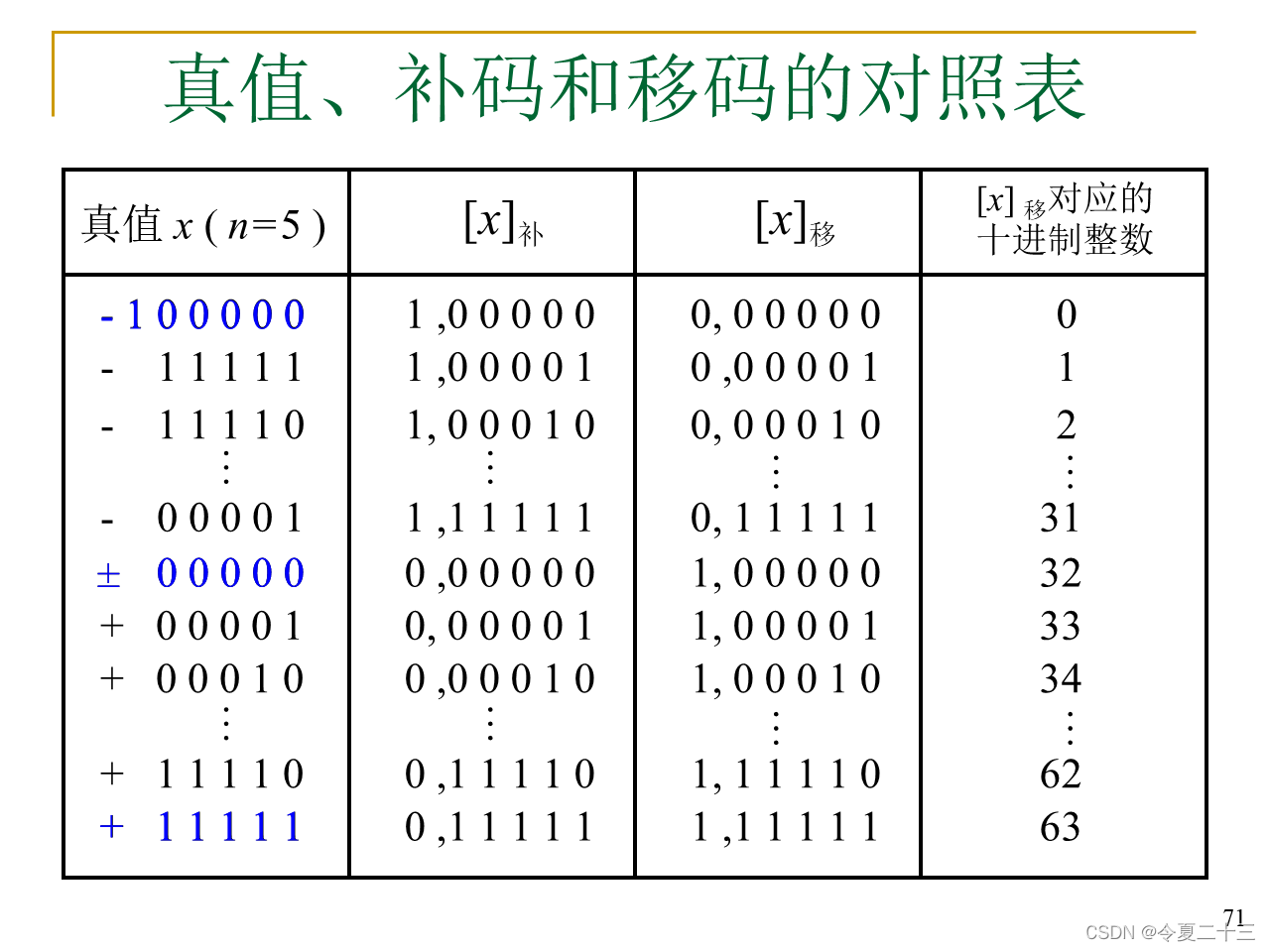
移码的定义

移码的特点

同一个真值的移码和补码只差一个符号位。
作业题知识点补充
1. 分数转换为二进制数
以 29/128 为例:
第一步
把分子和分母都转换为二进制,要表示为2的多少次。
那么分子表示为:2^4+2^3+2^2+2^0
那么分母呢:2^7
继续将他们写成分数形式:(2^4+2^3+2^2+2^0)/2^7。
接下来计算就好了,结果为:2^-3+2^-4+2^-5+2^-7。
第二步
讲一个小知识点:对于二进制数左移是放大2倍,右移是缩小2倍。
那么对于二进制1,我们右移得到0.1,缩小2倍。所以0.1代表1/2,即2-1。同理,0.01就是1/4,即2-2,以此类推。
有了这个基础,再看看上面的式子,不就是0.001+0.0001+0.000 01+0.000 0001。
用二进制加法计算出最后结果,即0.001 1101。
2. 无原码的特殊情况
补码为1.0000的真值为-1,但是没有原码,因为小数原码的范围如下:
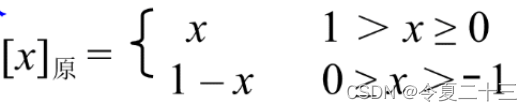
可知,小数1和-1都没有原码。
补码为1,0000的真值为-16,但也没有原码,因为整数原码的范围如下:
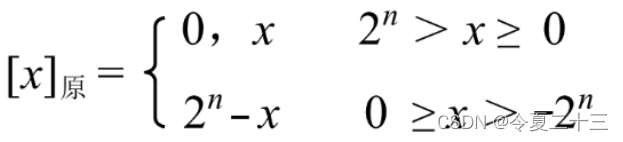
当数值位有四位时,原码的取值只能小于+16。
3. 十六进制转换为二进制
每个十六进制数都代表四位二进制数,所以直接按位置转换即可。
0 ~ 9 都可以当成十进制数化为二进制数,只是不足的要补足至四位,而剩下的则如下表所示:
| 十六进制 | 十进制 | 二进制 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
2.2 数的定点表示和浮点表示
2.1.1 定点表示

2.1.2 浮点表示

规格化数:浮点数的尾数以1开头,例如0.110101。
1. 浮点数的表示形式
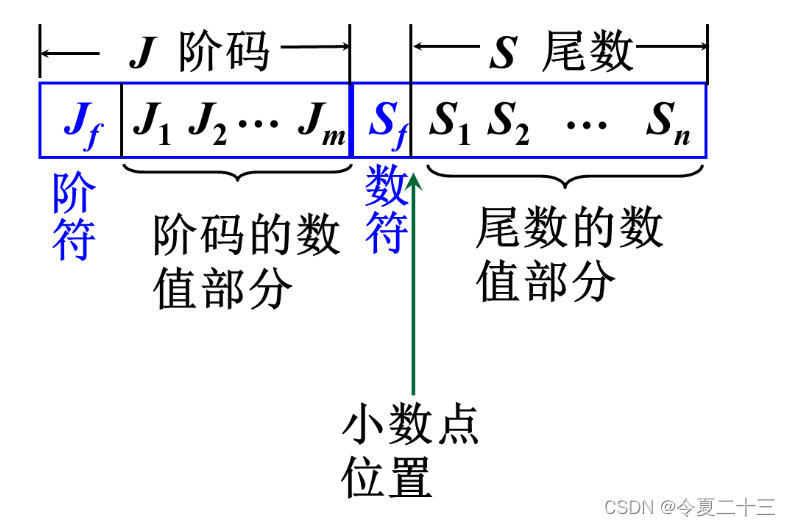

2. 浮点数的表示范围

3. 浮点数的规范化

2.2.3 定点数和浮点数的比较
- 当浮点机与定点机中的数其位数相同时,浮点数的表示范围比定点数大得多。(浮点机和定点记中的数都表示为机器数)
- 当浮点数为规格化数时,其精度远高于定点数。
- 浮点数运算分阶码和尾数部分,而且运算结果要求规格化。
- 在溢出的判断方法上,浮点数是对规格化的阶码进行判断,而定点数是对数值本身进行判断。
2.2.4 举例


机器零
- 当浮点数尾数为0时,不论其阶码是多少,按机器零处理;
- 当浮点数阶码等于或小于它能表示的最小数时,不论尾数是多少,按机器零处理
2.2.5 IEEE 754 标准
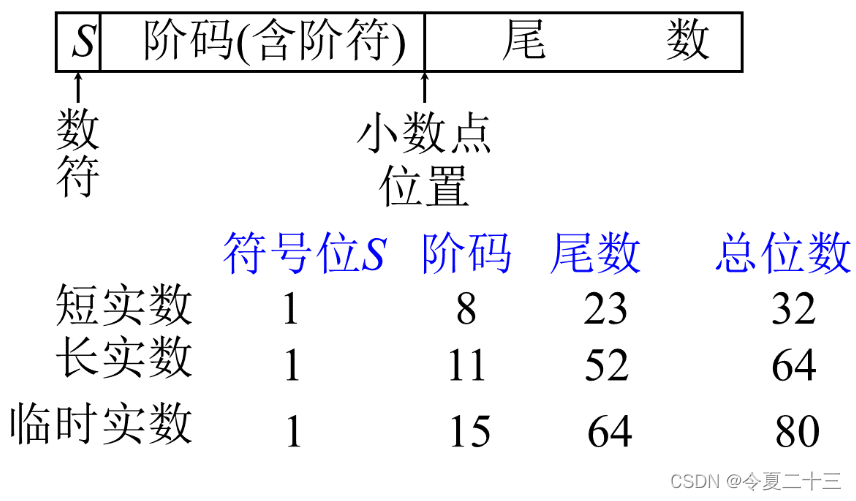
S:数符号,表示浮点数的正负,0为正,1为负;
阶码(含阶符):实际上是偏移阶码,求得阶码需要用原来的阶数加上不同长度实数对应的偏移量
偏移量:短实数(32位)127,长实数(64)1023
尾数:要先化为“1.xx……xx”的形式,再把最高位的“1”省略,只列出小数点后面的数,不足23位的要用0补齐


2.3 定点运算
2.3.1 移位运算
1. 移位的意义
定点移位,就是小数点的绝对位置不动,其余的数字全部向左或向右移动;
左移时,绝对值增大;右移时,绝对值减小。
在计算机中整移位运算很有用,让移位和加减配合就可以实现乘除运算。
算术移位:有符号数的移位,数值位在移位,符号位不变。
逻辑移位:无符号数的移位。
2. 算术移位规则
机器数移位后的空位添补规则
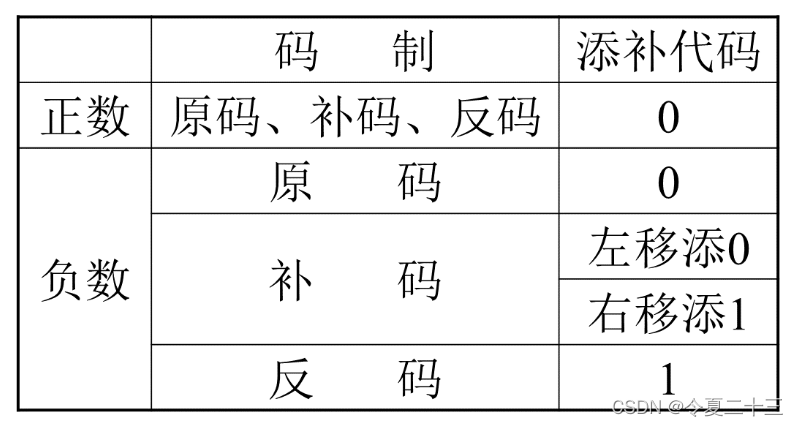
要注意,在算术移位中,移位前后符号位不变。
而逻辑移位中,左移时低位添0,高位丢弃;右移时高位添0,低位丢弃。
2.3.2 加减法运算
1. 补码加减运算公式


相关文章:

【机组】计算机系统组成课程笔记 第二章 计算机中的信息表示
2.1 无符号数和有符号数 2.1.1 无符号数 没有符号的数,其实就是非负数。在计算机中用字节码表示,目前最常用的是八位和十六位的。 2.1.2 有符号数 将正负符号数字化,0代表 ,1代表 - ,并把代表符号的数字放在有效数…...
指针笔试题详解
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.前言 2.指针题写出下列程序的结…...

MySQL 日志管理、备份与恢复
目录 1 数据备份的重要性 2 MySQL 日志管理 3 备份类型 3.1 数据备份的分类 3.2 备份方式比较 3.3 合理值区间 3.4 常见的备份方法 4 MySQL 完全备份与恢复 4.1 MySQL 完全备份 5 mysqldump 备份与恢复 5.1 MySQL 完全恢复 6 MySQL 增量备份与恢复 6.1 MySQL 增量…...
vtk- 数据类型(一) 三角链实例代码
三角链实例代码 #include <iostream> #include <string> #include <regex> #include "tuex.h" #include "vtkCylinderSource.h" #include "vtkPolyDataMapper.h" #include "vtkActor.h" #include "vtkRendere…...
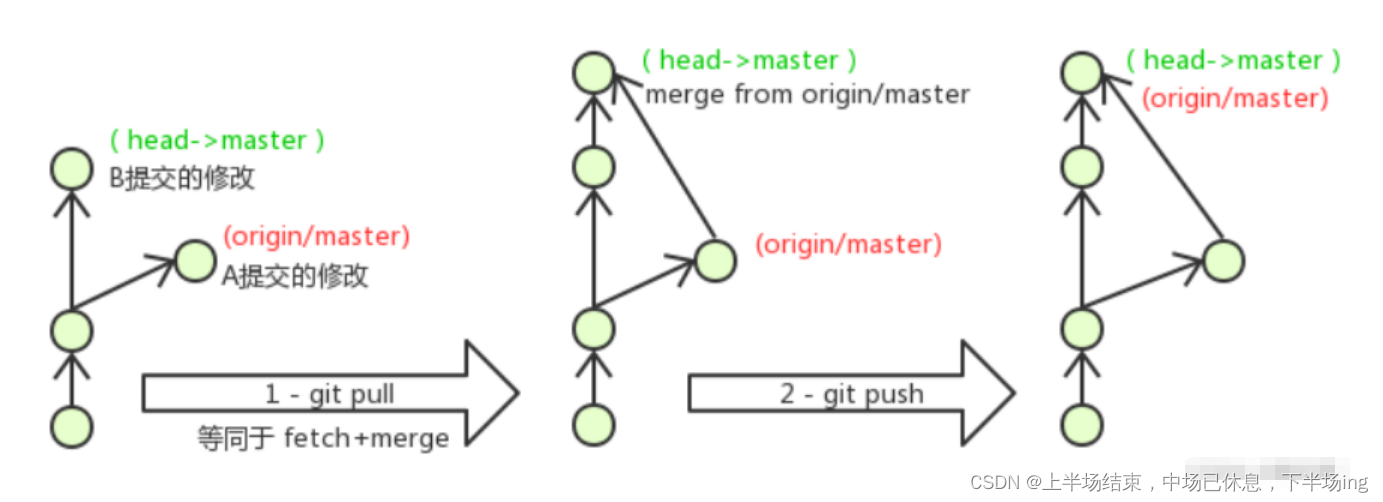
Git大全
目录 一、Git概述 1.1Git简介 1.2Git工作流程图 1.3查看Git的版本 1.4 Git 使用前配置 1.5为常用指令配置别名(可选) 1.5.1打开用户目录,创建 .bashrc 文件 1.5.2在 .bashrc 文件中输入如下内容: 1.5.3打开gitBash,执行…...

Touch命令使用指南:创建、更新和修改文件时间戳
文章目录 教程:touch命令的使用指南一、介绍1.1 什么是touch命令?1.2 touch命令的作用1.3 touch命令的语法 二、基本用法2.1 创建新文件2.2 更新文件时间戳2.3 创建多个文件2.4 修改文件访问时间2.5 修改文件修改时间2.6 修改文件创建时间 三、高级用法3…...

Windows开启 10 Telnet
在Windows 10中,Telnet客户端默认是不安装的。要在Windows 10上使用Telnet客户端,您需要手动启用它。以下是启用Telnet客户端的步骤: 打开控制面板。您可以通过在开始菜单中搜索"控制面板"来找到它。在控制面板中,选择…...

高教杯数学建模A题程序设计要点与思路
2023 年是我最后一次参加 高教杯大学生数学建模竞赛 以后不会再参加了(大四参加意义不太,研究生有研究生的数学建模大赛) 很遗憾 由于各种原因 我们没有能够完成赛题2022 年 美赛 2022年 Mathor Cup 2022 年国赛 2022 亚太杯 2023年 美赛 202…...

Spring Boot的新篇章:探索2.0版的创新功能
文章目录 引言1. Spring Boot 2.0的响应式编程2. 自动配置的改进3. Spring Boot 2.0的嵌入式Web服务器4. Spring Boot 2.0的Actuator端点5. Spring Boot 2.0的Spring Data改进6. Spring Boot 2.0的安全性增强7. Spring Boot 2.0的监控和追踪8. Spring Boot 2.0的测试改进结论 &…...
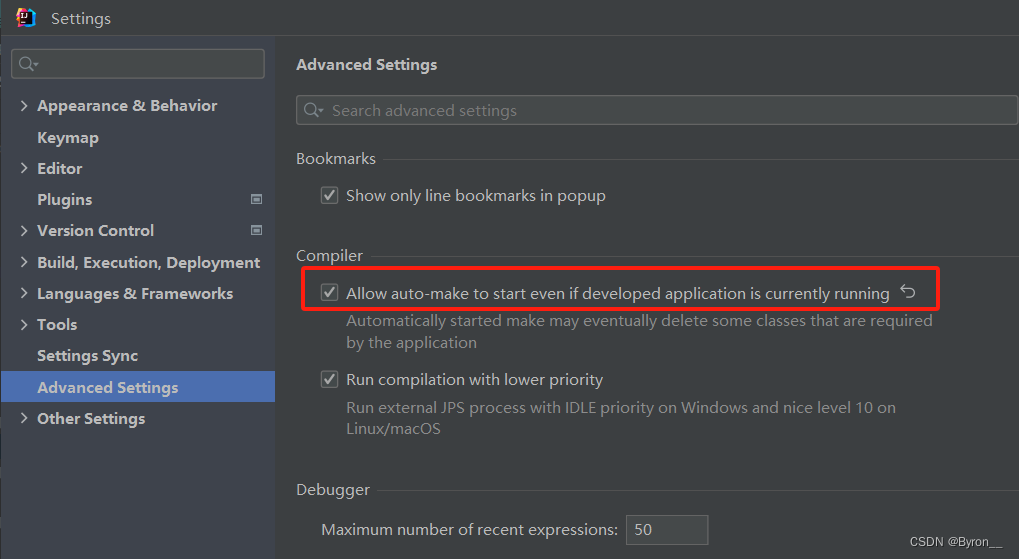
5、SpringBoot_热部署
六、热部署 1.热部署概述 概述:程序更改后,不需要重新启动服务器也能够实现动态更新 springboot 项目如何实现热部署? tomcat 已经内置到项目容器中了希望tomcat监听外部程序变化通过新建一个程序来监控你代码的变化 2.依赖导入 依赖 <…...
【kohya】训练自己的LoRA模型
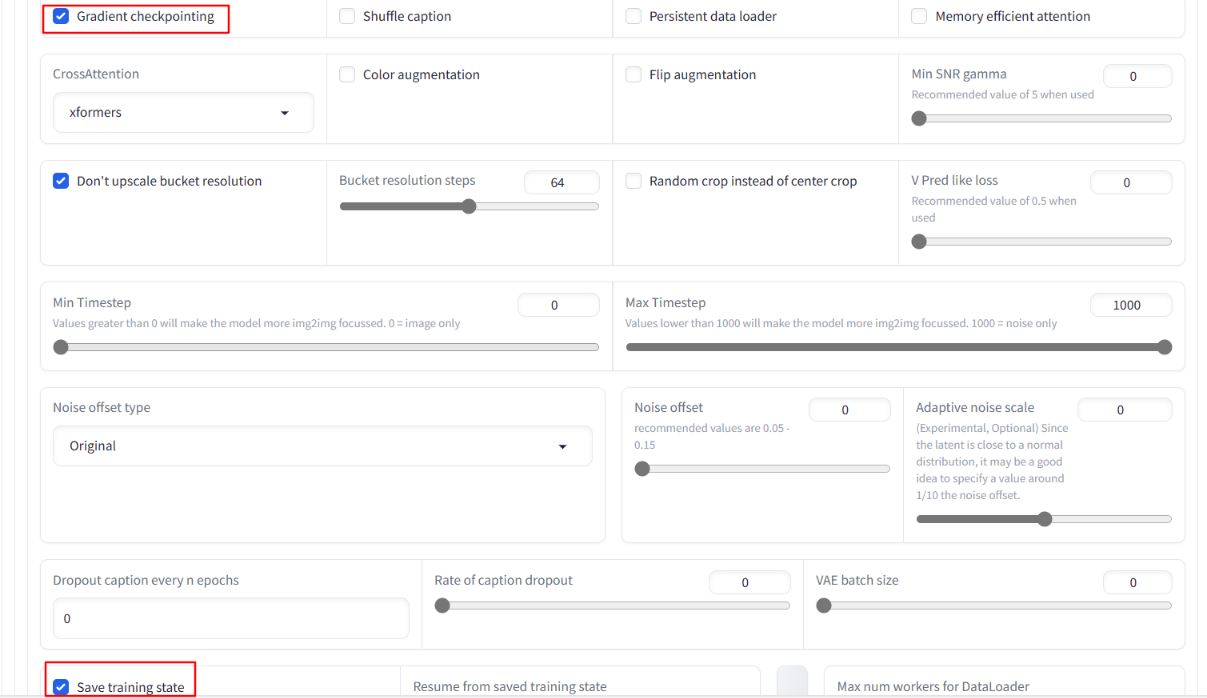
文章目录 序言准备环境准备图片处理图片下载kohya_ss代码修改pyvenv.cfg启动界面访问地址生成字幕准备训练的文件夹配置训练参数开始训练遇到的问题: 序言 在把玩stable diffusion的webUI和comfyUI后,思考着自己也微调一个个性化风格的checkpoint、LyCO…...
[尚硅谷React笔记]——第1章 React简介
目录: 第1章 React简介 React的基本使用:虚拟DOM的两种创建方式: 使用jsx创建虚拟DOM使用js创建虚拟DOM(一般不用)虚拟DOM与真实DOM:React JSX:JSX练习:模块与组件、模块化与组件化的理解 模块组件模块化组件化 第1章 React简介 中文官网: …...

Debezium系列之:快照参数详解
Debezium系列之:快照参数详解 一、snapshot.select.statement.overrides二、min.row.count.to.stream.results三、snapshot.delay.ms四、snapshot.fetch.size五、snapshot.lock.timeout.ms六、incremental.snapshot.allow.schema.changes七、incremental.snapshot.chunk.size八…...

redis单机版搭建
title: “Redis单机版搭建” createTime: 2022-01-04T20:43:1108:00 updateTime: 2022-01-04T20:43:1108:00 draft: false author: “name” tags: [“redis”] categories: [“install”] description: “测试的” redis单机版搭建 安装环境 redis版本redis-5.0.7虚拟机系统…...

物联网边缘网关
物联网边缘网关 边缘网关的定义边缘网关的分类边缘计算网关平台相关产品有哪些 百度边缘计算平台(BIE)华为边缘计算平台(IEF)产品应用拓扑图产品价格区间...

docker部署springboot程序时遇到的network问题
对应问题,因为刚开始接触docker,所以问题可能比较简单,但是做个记录 1、启动一个springboot项目获取本地ip的时候获取到的是172.17.0.x这个ip;在使用一些注册中心,mq的时候又要表明自己的本机器ip的时候会比较头疼&…...
RASP hook插桩原理解析
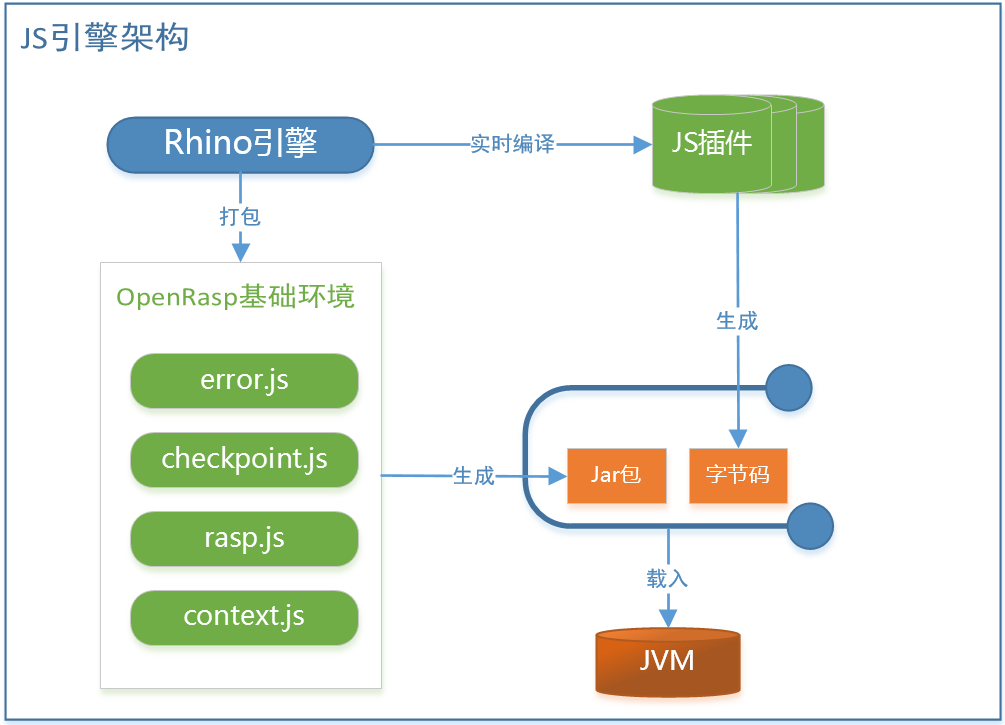
javaagent技术,实现提前加载类字节码实现hook,插桩技术 javassist技术ASM字节码技术 像加载jar,有两种方式 premain启动前加载:每次变动jar包内容,都需要进行重启服务器利用java的动态attch加载原理,采用pr…...
Pygame中Sprite的使用方法6-5
3 碰撞检测 蓝色方块会随着鼠标移动,当碰到绿色方块时,则当前分数加1,当碰到红色方块时,当前分数减1。因为要随时进行碰撞检测,因此需要在while True循环中实现以下功能。 3.1 蓝色方块随鼠标移动 将蓝色方块的位置…...

浅谈为什么多态只能是指针或引用
其实在很早之前,我一直没有注意到这个问题,直到今天碰见了一道题,顺便前面的博客中,继承写到,子类中不包含父类,子类只是继承了父类的成员变量和函数,由这一点,引发了我对切片以及赋…...

js看代码说输出
目录 原型 Function与Object new fn() 原型链 constructor function.length 默认参数:第一个具有默认值之前的参数个数 剩余参数:不算进length 闭包 循环中 函数工厂:形参传递 IIFE:匿名闭包 let:闭包 forEach()&am…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
