Leetcode 2866. Beautiful Towers II
- Leetcode 2866. Beautiful Towers II
- 1. 解题思路
- 2. 代码实现
- 题目链接:2866. Beautiful Towers II
1. 解题思路
这一题其实思路上还是比较明显的,就是一个单调数组的问题,问题在于说如果具体去设计这个单调数组。
我们从题目出发,具体来说,就是要构造一个山形数组,使得这个山形数组在给定的maxHeights的限制下能够面积最大,或者说累积和最大。
那么,我们不妨考察每一个位置作为山的山顶的情况下所能够构成的山形数组的面积,然后取出其中的最大值即可。
而这个问题又可以进一步拆解为,考察每一个位置作为山顶时,其左侧可以获得最大面积以及右侧可以获得的最大面积。此时,前者就是一个单调非减数组,而后者就是一个单调非增数组。而这两部分本质上又是相同的,因此,我们仅以左侧进行说明。
要求每一个位置作为山顶时左侧的这个最大的单调非增数组,那么对应可以采用的maxHeights一定也是一个单调递增的数组,因此,我们只需要构造一个数组,考察每一个位置的maxHeight[i]时,就弹出当前单调数组当中所有大于这个高度的值,直到剩下有一个更低的maxHeight[j]存在,此时能够获得的面积就是之前一个maxHeight[j]的面积加上maxHeight[i]*(i-j),也就是从第j+1到i的位置最多只能够取maxHeight[i],从而,我们就在 O ( N ) O(N) O(N)的时间复杂度上求得了所有位置作为山顶时,左侧可以取到的最大面积。
同样,我们反向即可求得右侧的最大面积,两者相加减去其本身(因为本身计算了两次)即为对应位置作为山顶时能够取到的最大面积。
最后,我们再从中获得最大值即可。
2. 代码实现
给出python代码实现如下:
class Solution:def maximumSumOfHeights(self, maxHeights: List[int]) -> int:n = len(maxHeights)left = [0 for _ in range(n)]s = []for i, h in enumerate(maxHeights):while s != [] and s[-1][0] >= h:s.pop()if s == []:s.append((h, i, h*(i+1)))else:_, j, r = s[-1]s.append((h, i, r + h*(i-j)))left[i] = s[-1][2]right = [0 for _ in range(n)]s = []for i in range(n-1, -1, -1):h = maxHeights[i]while s != [] and s[-1][0] >= h:s.pop()if s == []:s.append((h, i, h*(n-i)))else:_, j, r = s[-1]s.append((h, i, r + h*(j-i)))right[i] = s[-1][2]return max(left[i] + right[i] - maxHeights[i] for i in range(n))
提交代码评测得到:耗时862ms,占用内存42.5MB。
相关文章:

Leetcode 2866. Beautiful Towers II
Leetcode 2866. Beautiful Towers II 1. 解题思路2. 代码实现 题目链接:2866. Beautiful Towers II 1. 解题思路 这一题其实思路上还是比较明显的,就是一个单调数组的问题,问题在于说如果具体去设计这个单调数组。 我们从题目出发&#x…...

电脑C盘爆红怎么办?(小白篇)
文章目录 前言:1、清理临时和系统文件2、更改电脑默认软件安装位置3、微信、QQ文件存储路径放在其它盘4、卸载一些不常用的软件彩蛋 前言: C盘作为电脑的系统盘,如果出现爆满或者剩余空间很小整个C盘变红,这样会导致电脑系统运行…...

Office Xml 2003转XLSX
一、使用到的依赖包 1、xelem-3.1.jar 下载地址:管网下载地址 2、poi-3.17.jar 下载地址:https://mvnrepository.com/artifact/org.apache.poi/poi 二、实现方法 1、Xml2003公式转XLSX公式算法 (1)Xml2003函数格式 SUM(R[-1…...
)
skyWalking搭建(一)
title: “SkyWalking搭建(一)” createTime: 2021-07-27T14:34:2108:00 updateTime: 2021-07-27T14:34:2108:00 draft: false author: “name” tags: [“skywalking”] categories: [“java”] description: “测试的” 基于 docker 部署 skywalking 并实现 SpringBoot 全链路…...

Golang开发--sync.WaitGroup
sync.WaitGroup 是 Go 语言标准库中的一个并发原语,用于等待一组并发操作的完成。它提供了一种简单的方式来跟踪一组 goroutine 的执行状态,并在所有 goroutine 完成后恢复执行。 下面是关于 sync.WaitGroup 的实现细节的详细解释: 创建 Wa…...

Linux命令教程:使用cat命令查看和处理文件
文章目录 教程:使用cat命令在Linux中查看和处理文件1. 引言2. cat命令的基本概述3. 查看文件内容4. 创建文件5. 文件重定向和管道6. 格式化和编辑文件7. 实际应用示例7.1 使用cat命令浏览日志文件7.2 利用cat命令合并多个配置文件7.3 使用cat命令将文件内容发送到其…...
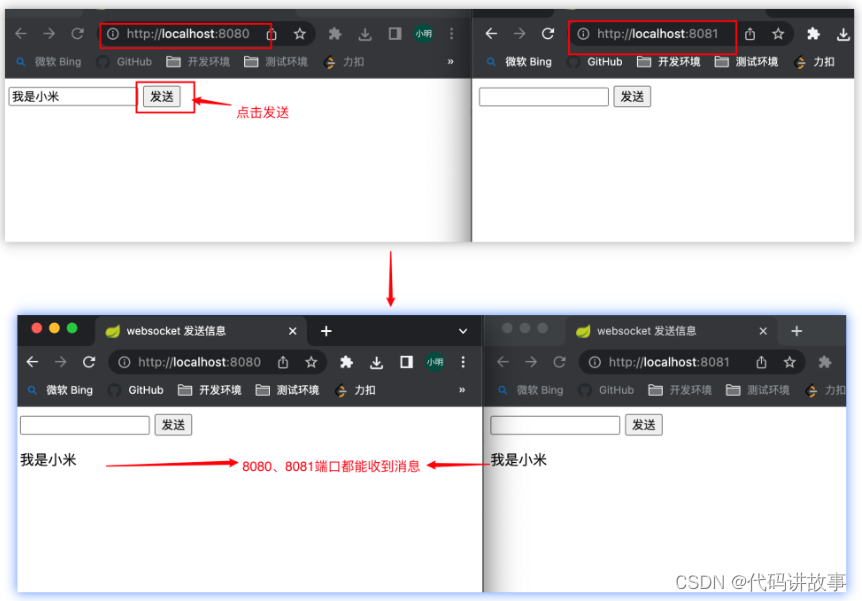
Websocket集群解决方案以及实战(附图文源码)
最近在项目中在做一个消息推送的功能,比如客户下单之后通知给给对应的客户发送系统通知,这种消息推送需要使用到全双工的websocket推送消息。 所谓的全双工表示客户端和服务端都能向对方发送消息。不使用同样是全双工的http是因为http只能由客户端主动发…...
)
科技的成就(五十一)
397、初等数论的不可解问题 1936 年 4 月,邱奇证明判定性问题不可解。33 岁的邱奇发表论文《初等数论的不可解问题》,运用λ演算给出了判定性问题一个否定的答案。λ演算是一套从数学逻辑中发展起来的形式系统,采用变量绑定和替换,…...
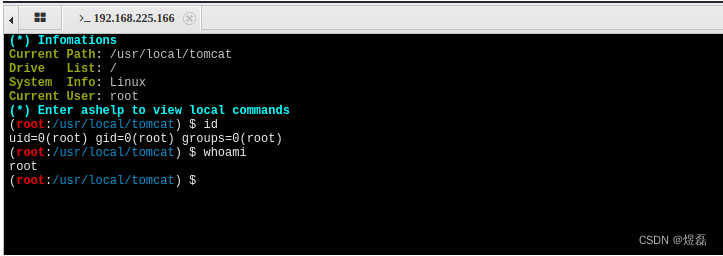
Tomcat8 任意写文件PUT方法 (CVE-2017-12615)
Tomcat 任意写文件PUT方法 (CVE-2017-12615) 文章目录 Tomcat 任意写文件PUT方法 (CVE-2017-12615)1 在线漏洞解读:2 版本影响3 环境搭建4 漏洞复现4.1 访问4.2 POC攻击点4.2.1 直接发送以下数据包,然后shell将被写入Web根目录。4.2.2 访问是否通,可以访…...

SAP服务器修改主机名操作手册
1、业务背景 SAP服务器P2V:虚拟化后的服务器主机名(或叫计算机名、设备名,hostname,下文同)会和原参照克隆的服务器主机名一样,若两台服务器处于同一网域,会出现域冲突,导致以下事故发生 (1)、使得原服务器出现掉域情况(DEV->CLN->PRD后台服务器访问失效) …...

【大数据】Doris 构建实时数仓落地方案详解(一):实时数据仓库概述
本系列包含: Doris 构建实时数仓落地方案详解(一):实时数据仓库概述Doris 构建实时数仓落地方案详解(二):Doris 核心功能解读Doris 构建实时数仓落地方案详解(三)&#…...
C++ list容器的实现及讲解
所需要的基础知识 对C类的基本了解 默认构造函数 操作符重载 this指针 引用 模板等知识具有一定的了解,阅读该文章会很轻松。 链表节点 template<class T>struct list_node{T _data;list_node<T>* _next;list_node<T>* _prev;list_node(const T&…...
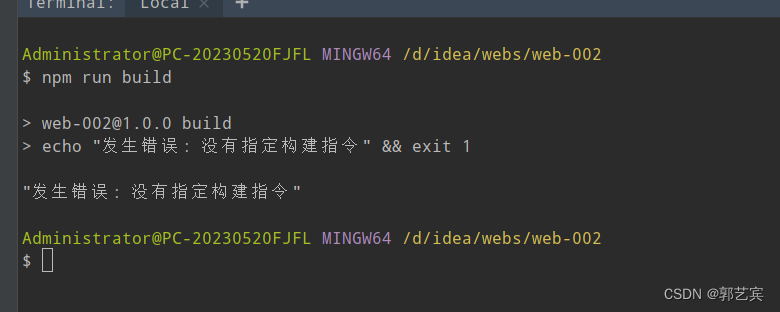
前端项目练习(练习-002-NodeJS项目初始化)
首先,创建一个web-002项目,内容和web-001一样。 下一步,规范一下项目结构,将html,js,css三个文件放到 src/view目录下面: 由于html引入css和js时,使用的是相对路径,所以…...
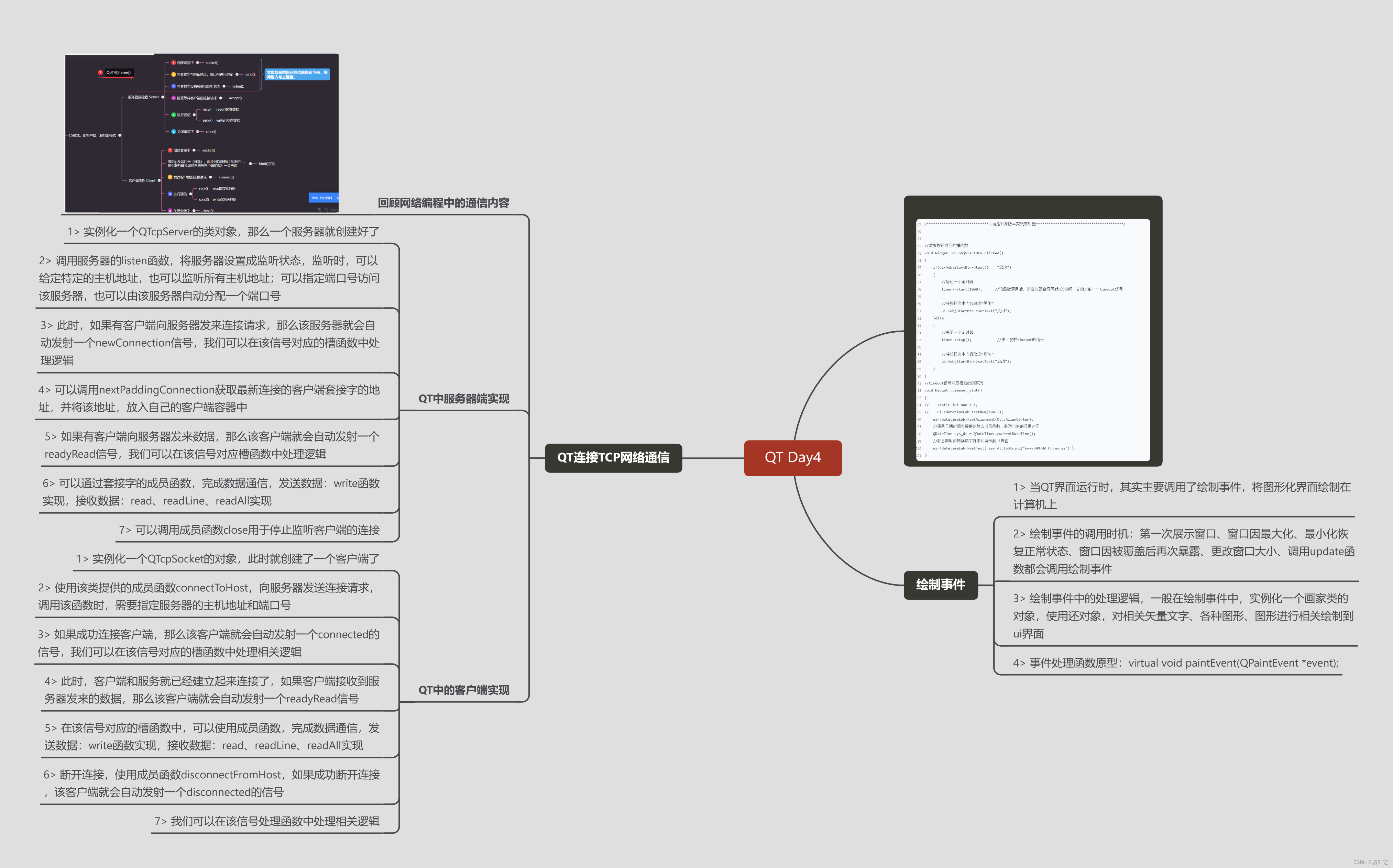
C++QT day11
绘制时钟 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPaintEvent>//绘制事件类 #include <QDebug>//信息调试类 #include <QPainter>//画家类 #include <QTimer>//定时器类 #include <QTime> #include &…...

Stable DIffusion 炫酷应用 | AI嵌入艺术字+光影光效
目录 1 生成AI艺术字基本流程 1.1 生成黑白图 1.2 启用ControlNet 参数设置 1.3 选择大模型 写提示词 2 不同效果组合 2.1 更改提示词 2.2 更改ControlNet 2.2.1 更改模型或者预处理器 2.2.2 更改参数 3. 其他应用 3.1 AI光影字 本节需要用到ControlNet,可…...

C#通过重写Panel改变边框颜色与宽度的方法
在C#中,Panel控件是一个容器控件,用于在窗体或用户控件中创建一个可用于容纳其他控件的面板。Panel提供了一种将相关控件组合在一起并进行布局的方式。以下是Panel控件的详细使用方法: 在窗体上放置 Panel 控件: 在 Visual Studio 的窗体设计器中,从工具箱中拖动并放置一…...
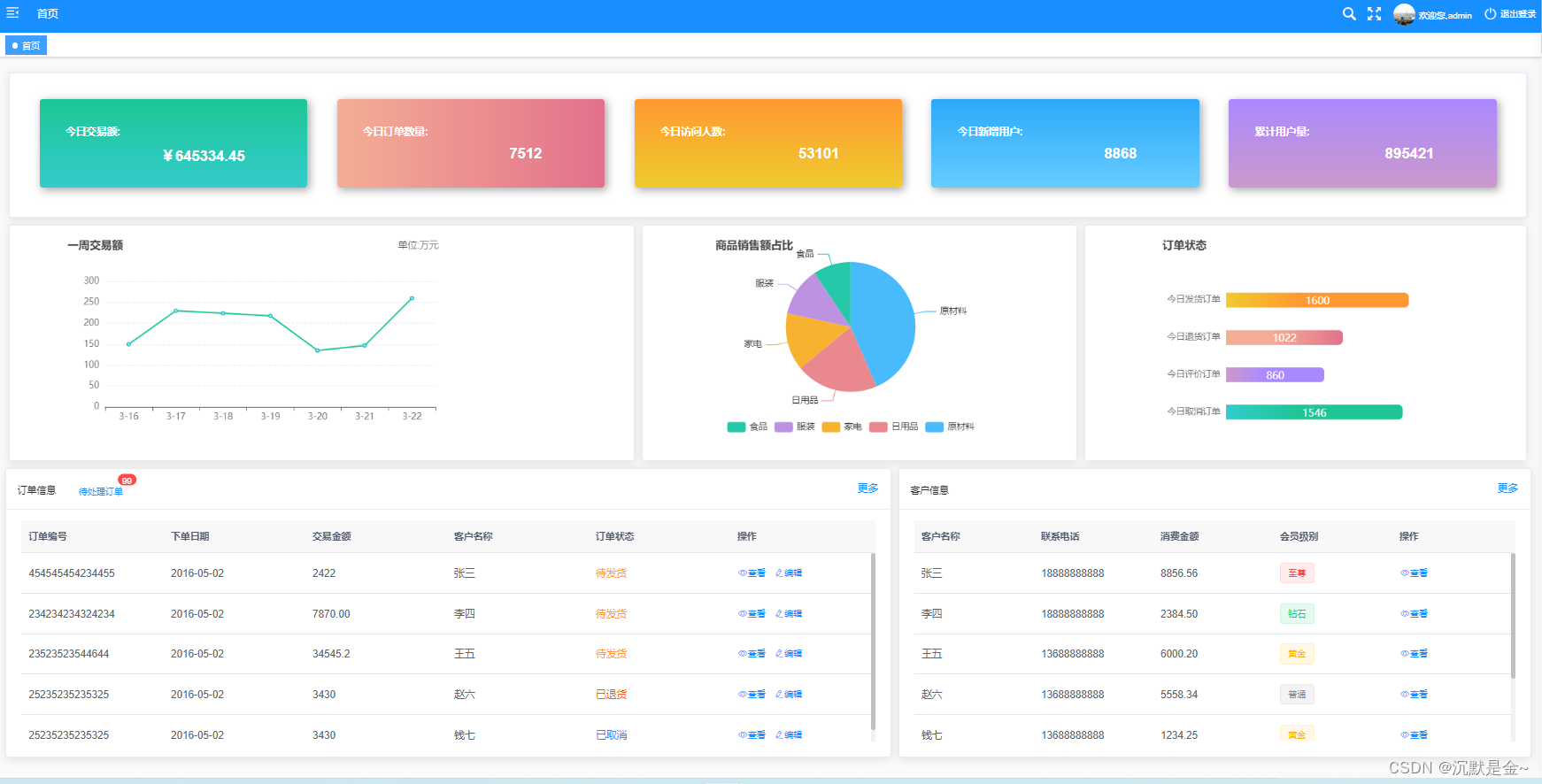
Vue2+ElementUI 静态首页案例
源码 <template><div class"app-container home"><el-row type"flex" justify"space-around" class"row-bg"><el-card class"box-card cardDiv1"><el-col :span"5"><div clas…...
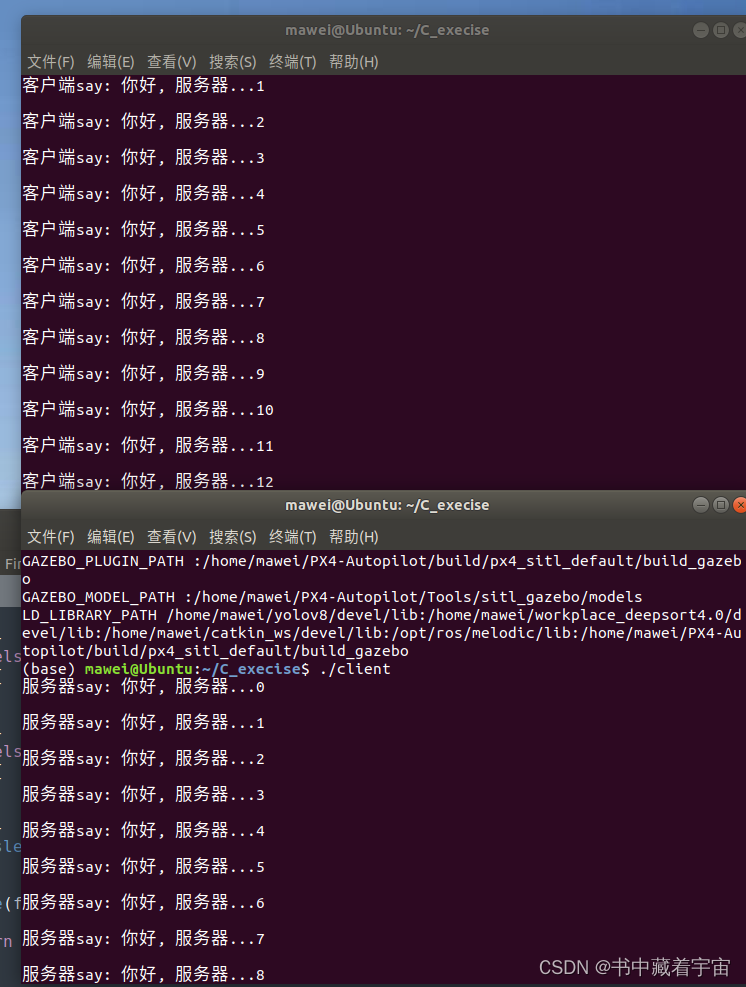
Linux的socket通信
关于套接字通信定义如下: 套接字对应程序猿来说就是一套网络通信的接口,使用这套接口就可以完成网络通信。网络通信的主体主要分为两部分:客户端和服务器端。在客户端和服务器通信的时候需要频繁提到三个概念:IP、端口、通信数据&…...

MySQL学习大纲
了解 MySQL 的基础知识和命令是使用此数据库的前提。以下是一些必须了解的 MySQL 概念和命令,包括基础的 CRUD(创建,读取,更新,删除)操作,以及一些高级功能: 1. 安装和启动 命令su…...

【Ambari】银河麒麟V10 ARM64架构_安装Ambari2.7.6HDP3.3.1(HiDataPlus)
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助🌸文…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
