堆的介绍与堆的实现和调整
个人主页:Lei宝啊
愿所有美好如期而遇
目录
堆的介绍:
关于堆的实现及相关的其他问题:
堆的初始化:
堆的销毁:
插入建堆:
堆向上调整:
交换两个节点的值:
堆向下调整:
删除根节点:
求堆顶数据:
打印堆的每一个节点的值:
堆排序:
堆的节点数量:
判断堆是否为空:
创建一个多数据文件:
TopK问题(综合):
向上/向下调整建堆哪个时间复杂度更优秀?
堆的介绍:
首先,堆是不完全二叉树。
不完全二叉树:除了最后一层外,其他层每一层都是满的,最后一层节点从左到右排。
再者,堆分为大堆和小堆。
大堆:父母节点的值大于等于孩子节点
小堆:父母节点的值小于等于孩子节点
关于堆的实现及相关的其他问题:
我们在主函数中将定义一个Heap hp;
typedef int Heaptype;
typedef struct Heap
{Heaptype* data;int size;int capacity;
}Heap;//堆的初始化
void HeapInit(Heap* php);
//堆的销毁
void HeapDestroy(Heap* php);
//插入建堆
void HeapPush(Heap* php, Heaptype num);
//堆向上调整
void Ajustup(Heaptype* a, int child);
//交换两个节点的值
void Swap(Heaptype* p1, Heaptype* p2);
//堆向下调整
void AjustDown(Heaptype* a, int n, int parent);
//删除根节点
void HeapPop(Heap* php);
//求得堆顶数据
Heaptype HeapTop(Heap* php);
//打印堆的每一个节点的值
void HeapPrint(Heaptype* arr, int size);
//堆排序
void HeapSort(Heaptype* arr, int size);
//堆的节点数量
void HeapSize(Heap* php);
//判读堆是否为空
void HeapEmpty(Heap* php);
//创建一个多数据文件
void CreateNDate();
//TopK问题
void PrintTopK(int k);堆的初始化:
void HeapInit(Heap* php)
{assert(php);php->data = NULL;php->size = 0;php->capacity = 0;
}
堆的销毁:
void HeapDestroy(Heap* php)
{assert(php);free(php->data);php->data = NULL;php->size = 0;php->capacity = 0;
}插入建堆:
void HeapPush(Heap* php, Heaptype num)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;Heaptype* temp = (Heaptype*)realloc(php->data, sizeof(Heaptype) * newcapacity);if (temp == NULL){perror("realloc fail");printf("\n%s", __LINE__);}php->data = temp;php->capacity = newcapacity;}php->data[php->size++] = num;//插入后当即向上调整,以保证还是个堆Ajustup(php->data, php->size - 1);
}堆向上调整:
//堆向上调整,调整一轮,建堆就循环插入去建
void Ajustup(Heaptype* a, int child)
{int parent = (child - 1) / 2;//当child == 0 的时候,parent也为0while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}交换两个节点的值:
void Swap(Heaptype* p1, Heaptype* p2)
{Heaptype temp = *p1;*p1 = *p2;*p2 = temp;}堆向下调整:
//堆向下调整
void AjustDown(Heaptype* a, int n, int parent)
{//从叶子节点开始int child = parent * 2 + 1;while (child < n){//找出最小孩子if (child + 1 < n && a[child] > a[child + 1]){child++;}else{if (a[parent] > a[child]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;} else{break;}}}}删除根节点:
void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);Swap(&php->data[0], &php->data[php->size - 1]);AjustDown(php->data, php->size - 1, 0);php->size--;
}求堆顶数据:
Heaptype HeapTop(Heap* php)
{assert(php);return php->data[0];
}打印堆的每一个节点的值:
void HeapPrint(Heaptype* arr, int size)
{assert(arr);for (int i = 0; i < size; i++){printf("%d ", arr[i]);}
}堆排序:
void HeapSort(Heaptype* arr, int size)
{assert(arr);//向上调整建堆(小堆)/*int num = size;for (int i = 0; i < num; i++){Ajustup(arr, i);}*///向下调整建堆int last = (size - 1 - 1) / 2;for (int i = last; i >= 0; i--){AjustDown(arr, size, i);}//排序int end = size - 1;while (end > 0){Swap(&arr[0], &arr[end]);AjustDown(arr, end, 0);end--;}
}堆的节点数量:
void HeapSize(Heap* php)
{assert(php);return php->size;
}判断堆是否为空:
void HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}创建一个多数据文件:
void CreateNDate()
{int n = 10000;srand((unsigned int)time(NULL));const char* file = "heap.txt";FILE* pf = fopen(file, "w");{if (pf == NULL){perror("fopen fail");return;}}for (int i = 0; i < n; i++){int num = rand() % 1000000;fprintf(pf, "%d\n", num);}fclose(pf);}
TopK问题(综合):
void PrintTopK(int k)
{Heaptype* arr = (Heaptype*)malloc(sizeof(Heaptype) * k); if (arr == NULL){perror("malloc fail");return;}FILE* pf = fopen("heap.txt", "r");if (pf == NULL){perror("fopen fail");return;}for (int i = 0; i < k; i++){fscanf(pf, "%d", &arr[i]);}//调整为小堆int n = (k - 1 - 1) / 2;for (int i = n; i >= 0; i--){AjustDown(arr, k, i);}//由于我们建1的是大小为k的堆,堆顶的数值最小,当新的数据大于堆//顶时,进堆,而堆顶的数据被替换,之后堆向下调整int a = 0;while (fscanf(pf, "%d", &a) != EOF){if (a > arr[0]){arr[0] = a;AjustDown(arr, k, 0);}}//此时堆里的数据是最大的k个数 for (int i = 0; i < k; i++){printf("%d ", arr[i]);}fclose(pf);free(arr);
}向上/向下调整建堆哪个时间复杂度更优秀?
答案是堆向下调整,时间复杂度为O(N),堆向上调整时间复杂度为O(N*logN)。

相关文章:

堆的介绍与堆的实现和调整
个人主页:Lei宝啊 愿所有美好如期而遇 目录 堆的介绍: 关于堆的实现及相关的其他问题: 堆的初始化: 堆的销毁: 插入建堆: 堆向上调整: 交换两个节点的值: 堆向下调整&a…...

【广州华锐互动】马属直肠检查3D虚拟仿真课件
随着科技的发展,医疗行业也在不断地进行创新。其中,广州华锐互动开发的马属直肠检查3D虚拟仿真课件,为医学教育和实践操作带来了新的可能性。它不仅可以帮助医生提高诊断准确率,还可以让医学生在没有真实病人的情况下进行实践操作…...

Nuxt 菜鸟入门学习笔记:路由
文章目录 路由 Routing页面 Pages导航 Navigation路由参数 Route Parameters路由中间件 Route Middleware路由验证 Route Validation Nuxt 官网地址: https://nuxt.com/ 路由 Routing Nuxt 的一个核心功能是文件系统路由器。pages/目录下的每个 Vue 文件都会创建一…...

C++基本语法和注释
C程序介绍 C 程序可以定义为对象的集合,这些对象通过调用彼此的方法进行交互。现在让我们简要地看一下什么是类、对象,方法、即时变量。 对象 - 对象具有状态和行为。例如:一只狗的状态 - 颜色、名称、品种,行为 - 摇动、叫唤、吃…...
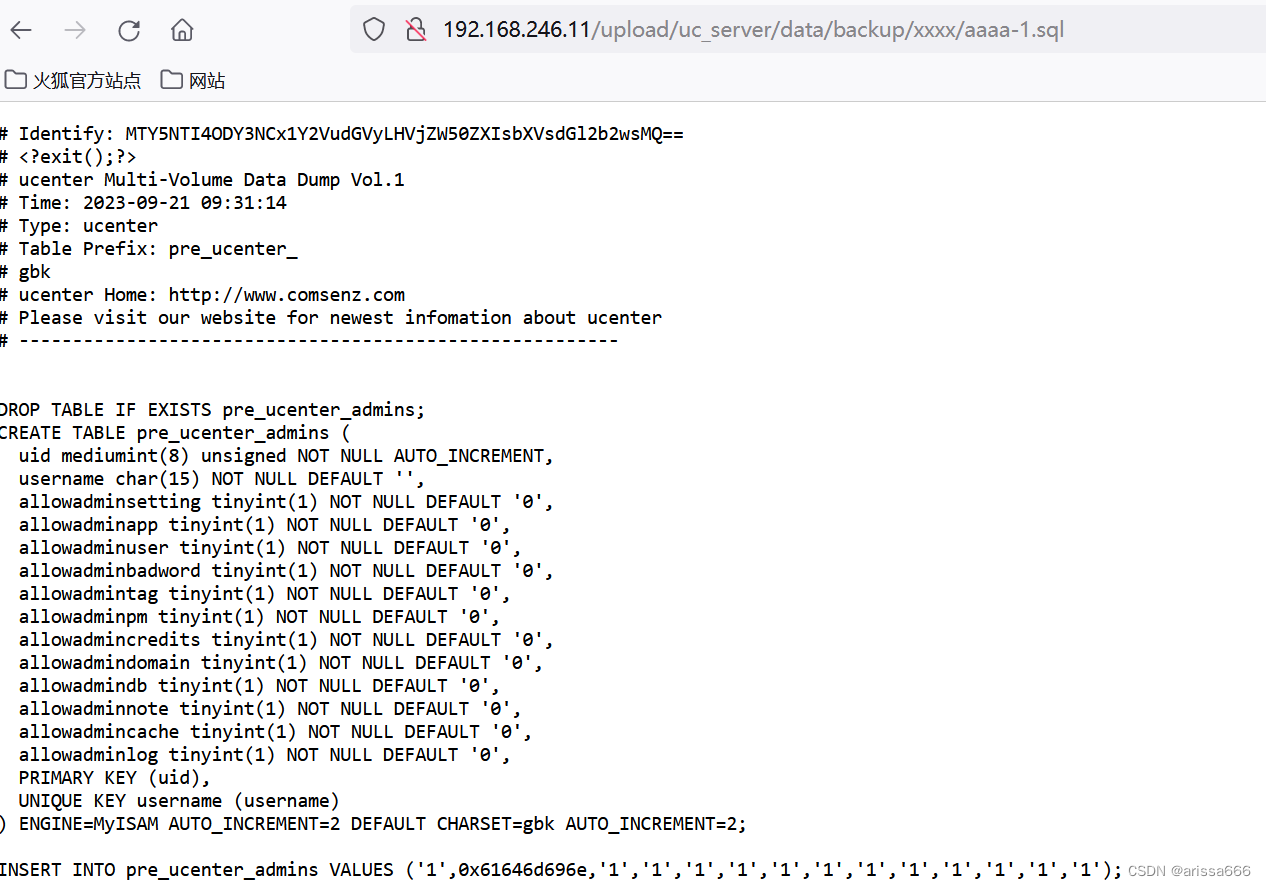
CSRF攻击
防御策略 过滤判断换referer头,添加tocken令牌验证,白名单 CSRF攻击和XSS比较 相同点:都是欺骗用户 不同点: XSS有攻击特征,所有输入点都要考虑代码,单引号过滤 CSRF没有攻击特征,利用的点…...

2023 “华为杯” 中国研究生数学建模竞赛(D题)深度剖析|数学建模完整代码+建模过程全解全析
问题一:区域碳排放量以及经济、人口、能源消费量的现状分析 思路: 定义碳排放量 Prediction 模型: CO2 P * (GDP/P) * (E/GDP) * (CO2/E) 其中: CO2:碳排放量 P:人口数量 GDP/P:人均GDP E/GDP:单位GDP能耗 CO2/E:单位能耗碳排放量 2.收集并统计相关…...
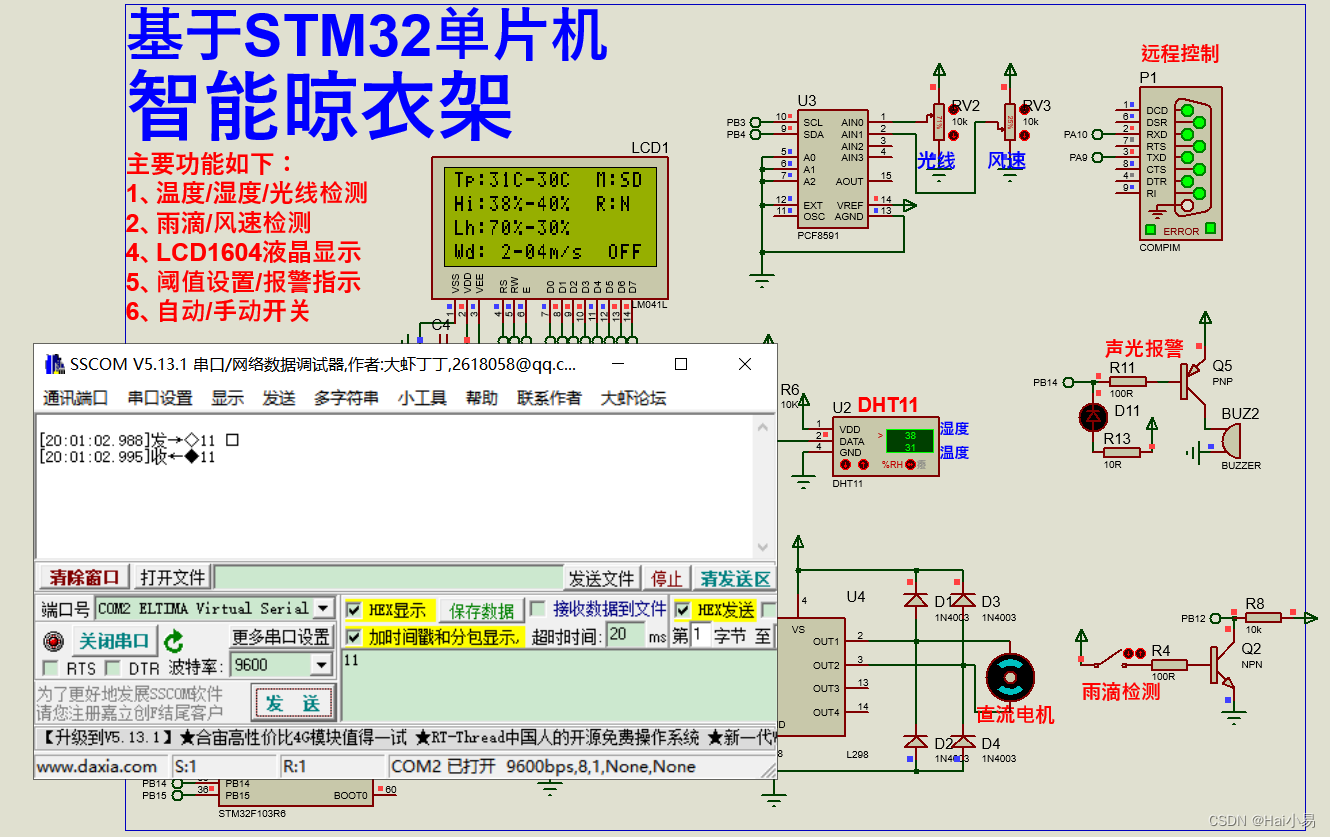
【Proteus仿真】【STM32单片机】基于单片机的智能晾衣架控制系统
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 系统运行后,LCD1604显示传感器检测的温湿度、光线强度和风速,工作模式,以及相应阈值,系统工作状态等;系统默认为自动模式, 可通过K4…...

C/C++代码静态检测工具PC-Lint常见错误总结
目录 1、PC-Lint 概述 2、PC-lint 常见错误列举 3、PC-Lint报告的语法错误 4、总结 VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到…...
概率深度学习建模数据不确定性
https://zhuanlan.zhihu.com/p/568912284理解论文 What uncertainties do we need in Bayesian deep learning for computer vision? (NeurIPS 2017) [1]中的数据不确定性建模,并给出公式推导。论文[1]指出不确定性uncertainty分为随机不确定性(aleator…...

Jenkins自动化部署前后端分离项目 (svn + Springboot + Vue + maven)有图详解
1. 准备工作 本文的前后端分离项目,技术框架是: Springboot Vue Maven SVN Redis Mysql Nginx JDK 所以首先需要安装以下: 在腾讯云服务器OpenCLoudOS系统中安装jdk(有图详解) 在腾讯云服务器OpenCLoudOS系统…...
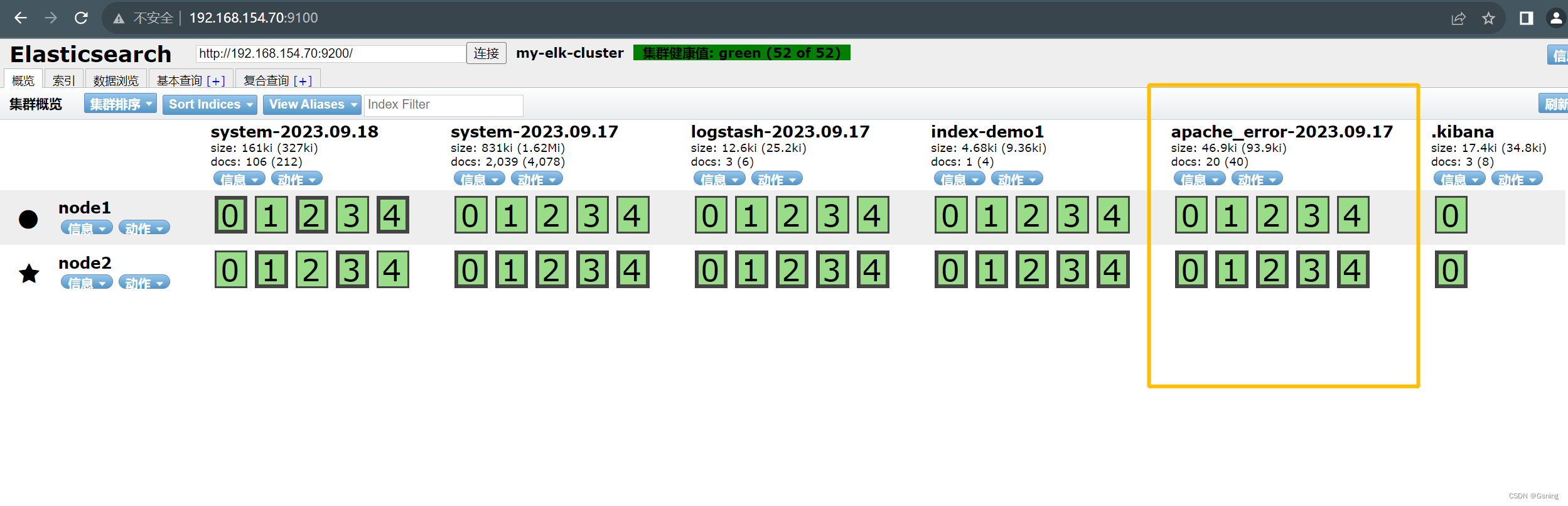
【ELK】日志系统部署
一、ELK日志分析系统 1、ELK的组成 ElasticSearchLogStashKibana ELK基于这三个开源日志的收集、存储、检索和可视化的解决方案;可帮助用户快速定位和分析应用程序的故障,监控应用程序性能和安全,以及提供丰富的数据分析和展示功能。 2、完…...

【算法挨揍日记】day08——30. 串联所有单词的子串、76. 最小覆盖子串
30. 串联所有单词的子串 30. 串联所有单词的子串 题目描述: 给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。 s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。 例如,如果 words ["…...
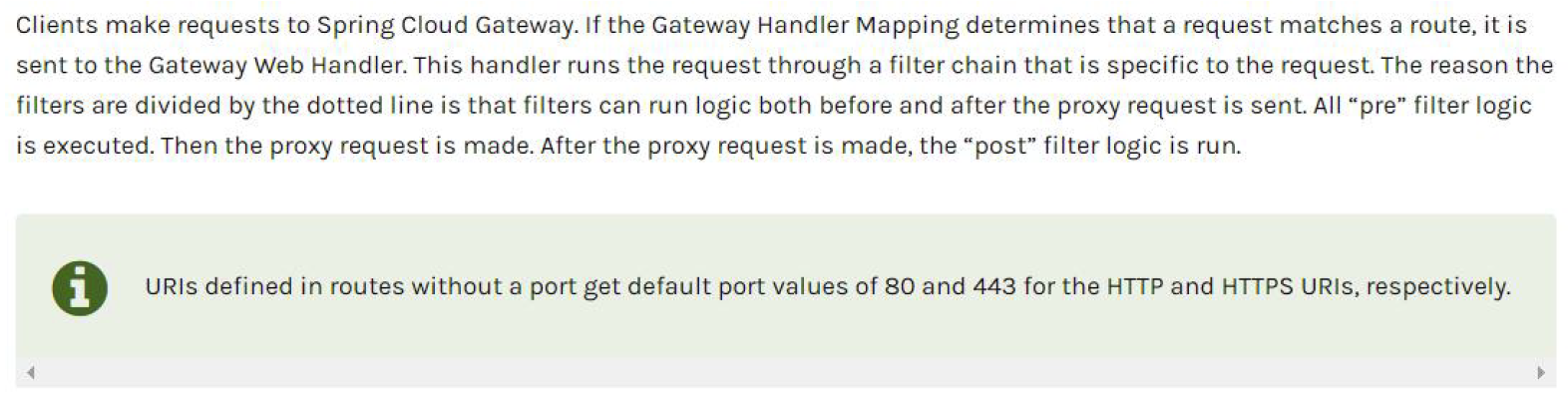
SpringCloud Gateway--网关服务基本介绍和基本原理
😀前言 本篇博文是关于SpringCloud Gateway的基本介绍,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以帮助到大家,您的满意是我的动力…...

使用Vue-cli构建spa项目及结构解析
一,Vue-cli是什么? 是一个官方发布的Vue脚手架工具,用于快速搭建Vue项目结构,提供了现代前端开发所需要的一些基础功能,例如:Webpack打包、ESLint语法检查、单元测试、自动化部署等等。同时,Vu…...
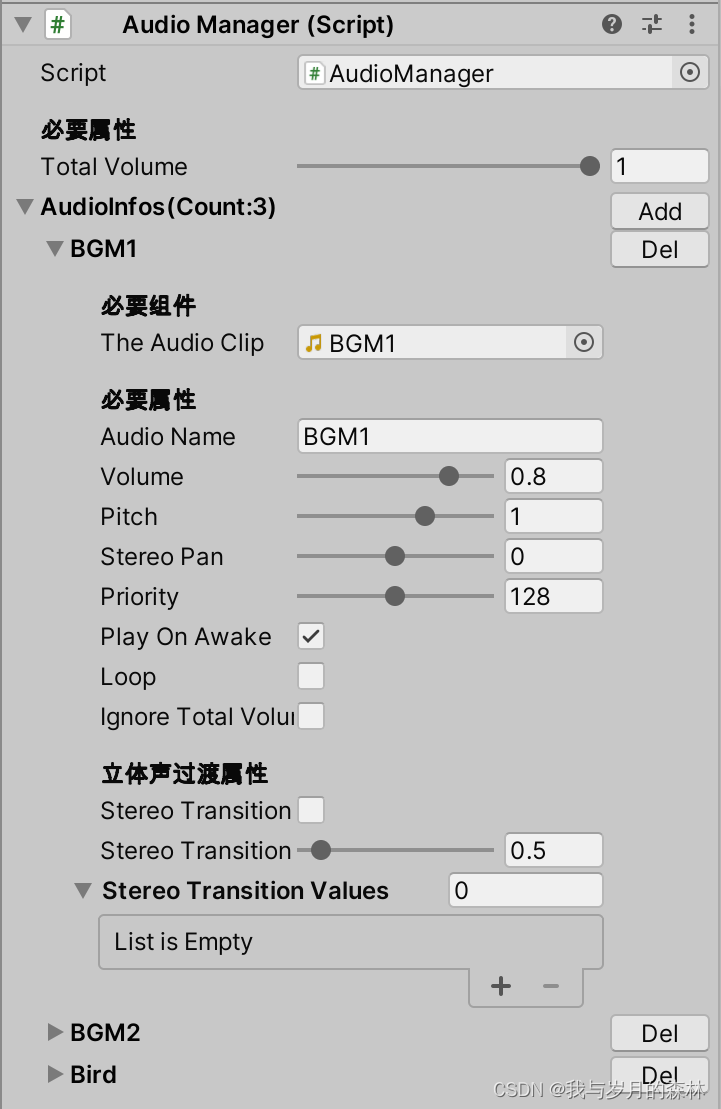
自定义Unity组件——AudioManager(音频管理器)
需求描述 在游戏开发中,音频资源是不可或缺的,通常情况下音频资源随机分布,各个音频的操作和管理都是各自负责,同时对于音频的很多操作逻辑都是大同小异的,这就造成了许多冗余代码的堆叠,除此之外在获取各类…...

leetcode 558 设计内存文件系统
题目 Design an in-memory file system to simulate the following functions: ls: Given a path in string format. If it is a file path, return a list that only contains this files name. If it is a directory path, return the list of file and directory namesin th…...
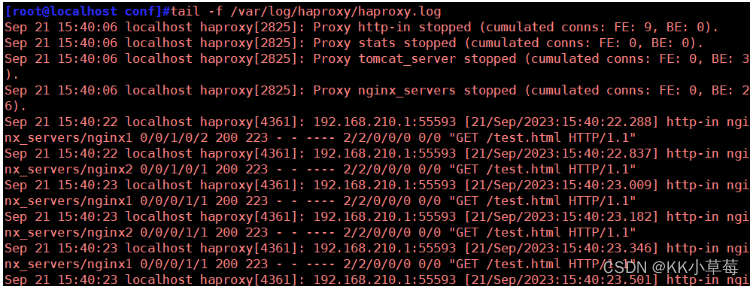
Haproxy负载均衡群集
HAproxy搭建Web群集一、Web集群调度器1、常见的Web集群调度器2、常用集群调度器的优缺点(LVS ,Nginx,Haproxy)2.1 Nginx2.2 LVS2.3 Haproxy 3、LVS、Nginx、HAproxy的区别 二、Haproxy1、简介2、Haproxy应用分析3、HAProxy的主要特性4、Haproxy调度算法(…...

什么是面包屑导航?
面包屑导航(Breadcrumb Navigation)这个概念来自童话故事“汉赛尔和格莱特”,当汉赛尔和格莱特穿过森林时,不小心迷路了,但是他们发现沿途走过的地方都撒下了面包屑,让这些面包屑来帮助他们找到回家的路。 在网站应用中࿰…...
VS2019创建GIt仓库时剔除文件或目录
假设本地有解决方案“SomeSolution” 1、首先”团队资源管理器“-“创建Git存储库”,选择“仅限本地”、“创建” VS会在解决方案目录下自动生成.gitattributes、.gitignore 2、编辑gitignore,直接拖到VS里或者用记事本打开。添加要剔除的文件或文件夹…...

计算机等级考试—信息安全三级真题六
目录 一、单选题 二、填空题 三、综合题 一、单选题...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
