【学习笔记】CF1103D Professional layer
首先分析不出啥性质,所以肯定是暴力优化😅
常见的暴力优化手段有均摊,剪枝,数据范围分治(points),答案值域分析之类的。
比较经典的题目是 CF1870E Another MEX Problem,可以用剪枝和分析值域两种方法通过
考虑剪枝,这个大佬 是剪枝高手,大家快去膜拜他🤩
首先,设 g = gcd 1 ≤ i ≤ n a i g=\gcd_{1\le i\le n} a_i g=gcd1≤i≤nai,然后对每个 a i a_i ai只保留 g g g中的质因数。发现此时本质不同的 a i a_i ai比较少,并且本质不同的质因数也比较少,考虑从这两方面入手
记质因数数目为 M M M, a i a_i ai的状态数为 m m m,显然 M ≤ 11 M\le 11 M≤11, m m m不太清楚,但是可以感性发现不会很大
发现对于相同的 a i a_i ai,只需要保留前 M M M个较小的 e i e_i ei即可,后面的都用不上。
同时注意到被操作的数不会超过 M M M,因此 D P DP DP复杂度为 O ( 3 M m M 2 ) O(3^MmM^2) O(3MmM2)
每次只加入一个 a i a_i ai太浪费了,可以考虑一次将相同的 a i a_i ai一起加进去,然后记录需要选择的 a i a_i ai数目的最小值。这样组外 D P DP DP的复杂度为 O ( 3 M m M ) O(3^MmM) O(3MmM),组内 D P DP DP的复杂度为 O ( 3 M m ) O(3^Mm) O(3Mm)。
当 M M M取遍所有值时,最大计算量在 1 0 8 10^8 108左右,可以通过。
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define ll long long
#define db double
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int N=1e6+5;
int n,cnt;
ll K,a[N],nums[N],e[N],g,res;
int M;
ll prime[15];
vector<ll>v[15005];
ll gcd(ll x,ll y){return y==0?x:gcd(y,x%y);
}
int get(ll x){return lower_bound(nums+1,nums+1+cnt,x)-nums;
}
void dfs(int u,ll mul){if(u==M){nums[++cnt]=mul;return;}while(mul<=1000000000000/prime[u]){mul*=prime[u],dfs(u+1,mul);}
}
ll now[1<<11][12],nxt[1<<11][12],sm[12];
int dp[1<<11],h[1<<11];
ll b[15];
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>K;for(int i=1;i<=n;i++)cin>>a[i],g=gcd(g,a[i]);for(int i=1;i<=n;i++)cin>>e[i];ll tmp=g;for(int i=2;i<=tmp/i;i++){if(tmp%i==0){prime[M++]=i;while(tmp%i==0)tmp/=i;}}if(tmp>1)prime[M++]=tmp;dfs(0,1),sort(nums+1,nums+1+cnt);for(int i=1;i<=n;i++){ll tmp2=1;for(int j=0;j<M;j++){while(a[i]%prime[j]==0)a[i]/=prime[j],tmp2*=prime[j];}v[get(tmp2)].pb(e[i]);}memset(now,0x3f,sizeof now),now[0][0]=0;for(int i=1;i<=cnt;i++){if(v[i].size()==0)continue;sort(v[i].begin(),v[i].end());if(v[i].size()>M)v[i].resize(M);for(int j=0;j<v[i].size();j++)sm[j+1]=sm[j]+v[i][j];ll tmp=nums[i];for(int j=0;j<M;j++){b[j]=1;while(tmp%prime[j]==0)b[j]*=prime[j],tmp/=prime[j];}for(int j=0;j<1<<M;j++){for(int k=0;k<=M;k++){nxt[j][k]=now[j][k];}}for(int j=1;j<1<<M;j++){h[j]=0,dp[j]=114514;ll mul=1;for(int k=0;k<M;k++){if(j>>k&1)mul*=b[k];}if(mul<=K)h[j]=1;for(int k=j;k;k=(k-1)&j){if(h[k])dp[j]=min(dp[j],dp[j-k]+1);}if(dp[j]<=v[i].size()){int s=(1<<M)-1-j;for(int k=s;;k=(k-1)&s){for(int l=0;l<=M;l++){if(now[k][l]!=inf){nxt[k+j][l+dp[j]]=min(nxt[k+j][l+dp[j]],now[k][l]+sm[dp[j]]);}}if(k==0)break;}}}for(int j=0;j<1<<M;j++){for(int k=0;k<=M;k++){now[j][k]=nxt[j][k];}}}ll res=inf;for(int i=0;i<=M;i++)if(now[(1<<M)-1][i]!=inf)res=min(res,now[(1<<M)-1][i]*i);cout<<(res==inf?-1:res);
}
相关文章:

【学习笔记】CF1103D Professional layer
首先分析不出啥性质,所以肯定是暴力优化😅 常见的暴力优化手段有均摊,剪枝,数据范围分治(points),答案值域分析之类的。 比较经典的题目是 CF1870E Another MEX Problem,可以用剪枝…...

vue之Pinia
定义 Store | Pinia 开发文档 1.什么是Pinaia Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。 2.理解Pinaia核心概念 定义Store 在深入研究核心概念之前,我们得知道 Store 是用 defineStore() 定义的,它的第一个参数要求是一…...
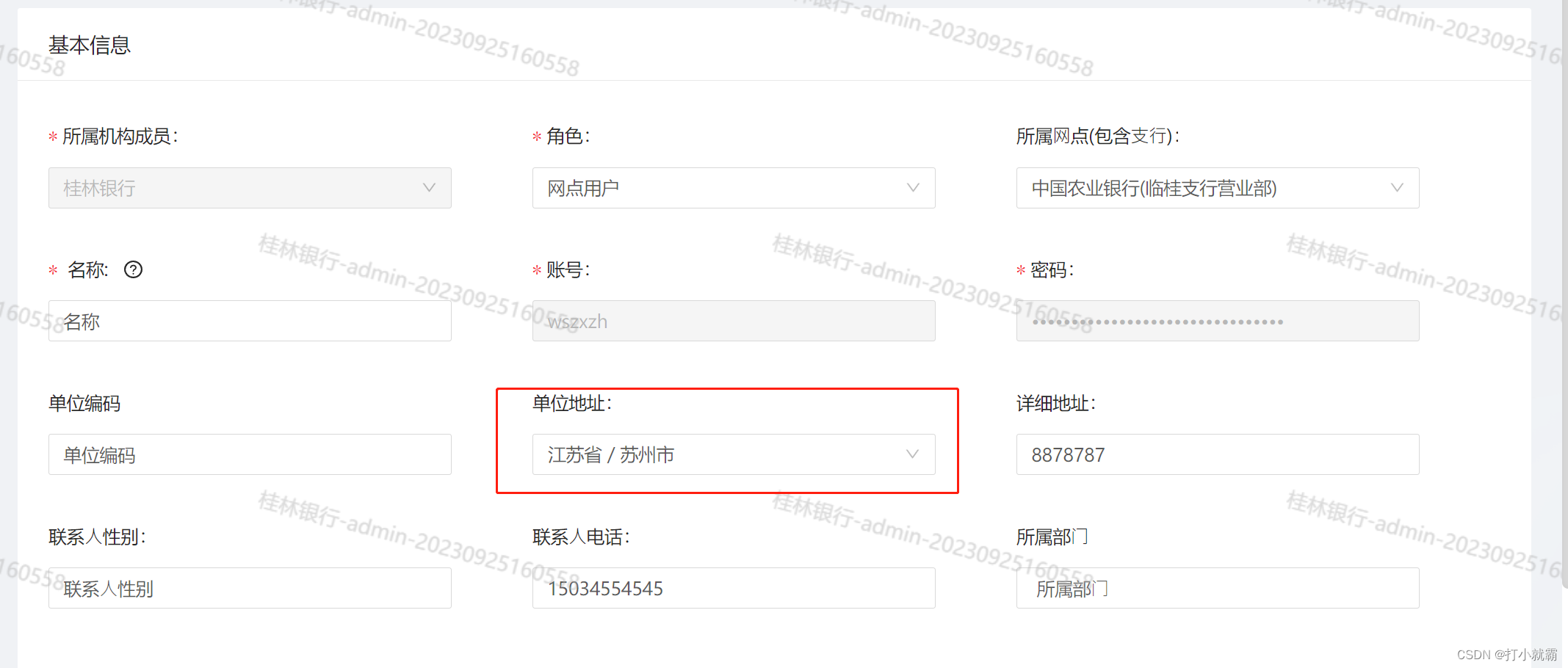
antd-vue 级联选择器默认值不生效解决方案
一、业务场景: 最近在使用Vue框架和antd-vue组件库的时候,发现在做编辑回显时** 级联选择器** 组件的默认值不生效。为了大家后面遇到和我一样的问题,给大家分享一下 二、bug信息: 三、问题原因: 确定不了唯一的值&a…...
分享53个Python源码源代码总有一个是你想要的
分享53个Python源码源代码总有一个是你想要的 链接:https://pan.baidu.com/s/1ew3w2_DXlSBrK7Mybx3Ttg?pwd8888 提取码:8888 项目名称 100-Python ControlXiaomiDevices DRF-ADMIN 后台管理系统 FishC-Python3小甲鱼 Flask框架的api项目脚手架 …...
【每日一题】658. 找到 K 个最接近的元素
658. 找到 K 个最接近的元素 - 力扣(LeetCode) 给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。 整数 a 比整数 b 更接近 …...
)
并发任务队列(字节青训测试题)
需求描述 封装一个并发任务队列类,用于对一些异步任务按指定的并发数量进行并发执行。 /*** 延迟函数* param {number} time - 延迟时间* return {Promise} delayFn - 延迟函数(异步封装)*/ function timeout(time) {return new Promise((resolve) > {setTimeo…...
Ubuntu 安装Nacos
1、官网下载最新版nacos https://github.com/alibaba/nacos/releases 本人环境JDK8,Maven3.6.3,启动Nacos2.2.1启动失败,故切换到2.1.0启动成功 2、放到服务器目录下,我的在/home/xxx/apps下 3、解压 $ tar -zxvf nacos-serve…...

CSS 小球随着椭圆移动
html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><…...
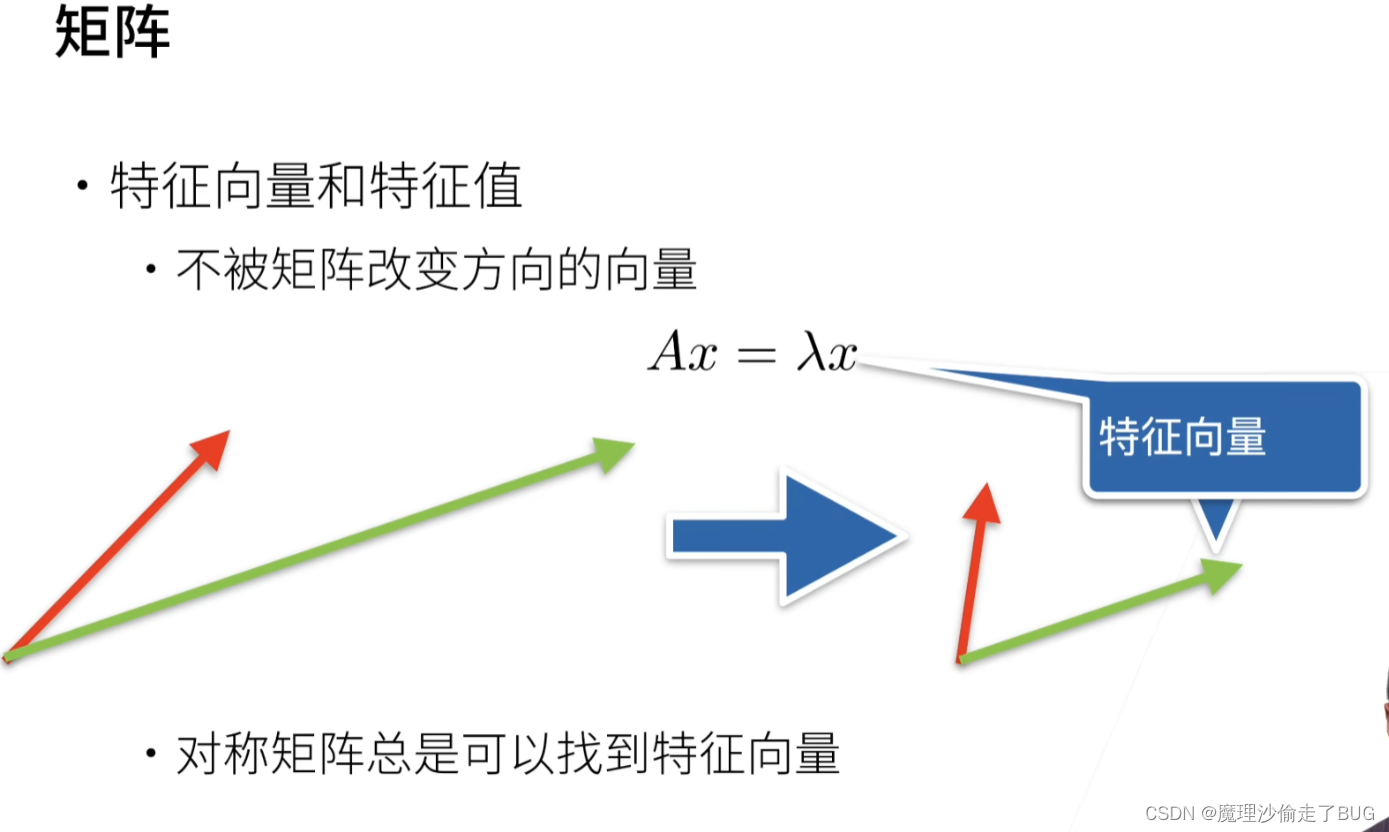
【李沐深度学习笔记】线性代数
课程地址和说明 线性代数p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性代数 标量 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,…...

vuejs - - - - - 递归组件的实现
递归组件的实现 1. 需求描述:2. 效果图:3. 代码3.1 封装组件代码3.2 父组件使用 1. 需求描述: 点击添加行,增加一级目录结构当类型为object or array时,点击右侧➕,增加子集点击右侧🚮&#x…...

精准对接促合作:飞讯受邀参加市工信局举办的企业供需对接会
2023年9月21日,由惠州市工业和信息化局主办的惠州市工业软件企业与制造业企业供需对接会成功举办,对接会旨在促进本地工业软件企业与制造业企业的紧密合作,推动数字化转型的深入发展。此次会议在市工业和信息化局16楼会议室举行,会…...

数学建模之遗传算法
文章目录 前言遗传算法算法思想生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配变异混合产生新种群 停止迭代的条件遗传算法在01背包中的应用01背包问题介绍01背包的其它解法01背包的遗传算法解法生物的表示初始种群的生成下一代种群的产生适应度函数轮盘赌交配…...

ISO9001认证常见的不符合项
今天,整理了一些关于ISO9001质量管理体系审核最常见的不合格项,以供大家参考。 一、质量管理体系 1、质量手册(标准条款4.2.2) (1)各部门执行的文件与手册的规定不一致。 (2)质量…...
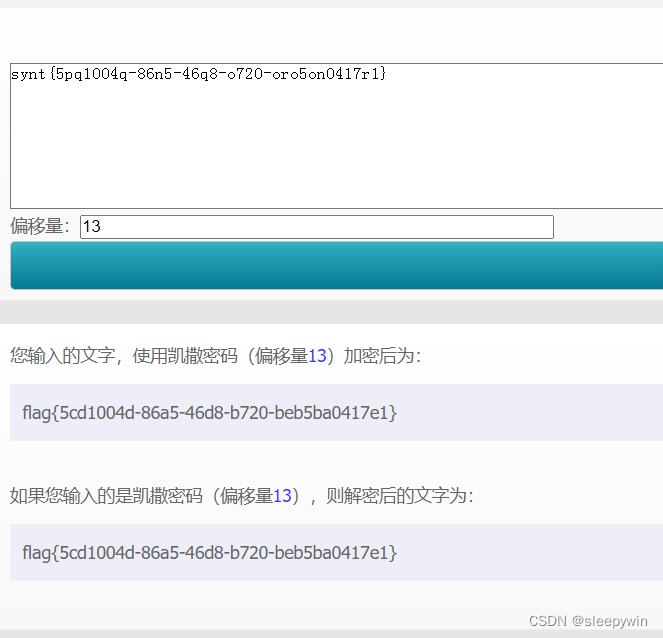
crypto:看我回旋踢
题目 下载压缩包后解压可得到提示文本 经过观察,synt{}这个提示与flag{}形式很像 由题目名中的回旋可以推测为凯撒密码,由凯撒密码的定义可知,需要先推出移位数,s->f数13次,因此移位数为13,解码可得...
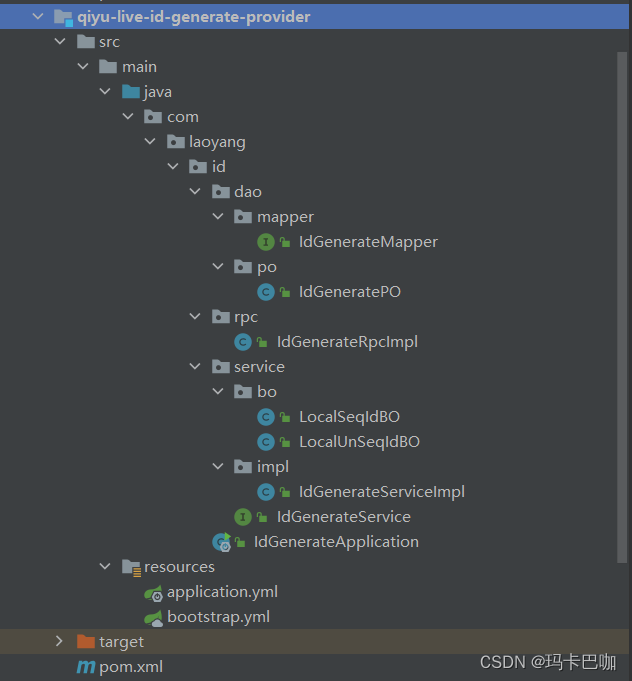
Springcloud实战之自研分布式id生成器
一,背景 日常开发中,我们需要对系统中的各种数据使用 ID 唯一表示,比如用户 ID 对应且仅对应一个人,商品 ID 对应且仅对应一件商品,订单 ID 对应且仅对应 一个订单。我们现实生活中也有各种 ID ,比如身…...
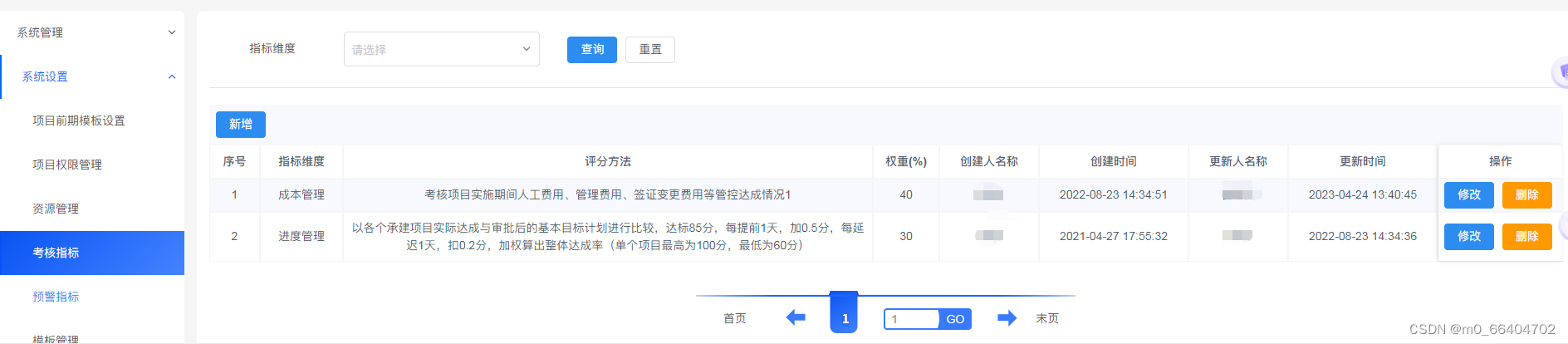
java 企业工程管理系统软件源码 自主研发 工程行业适用
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&am…...

Spring Cloud Alibaba Nacos 2.2.3 (4) - 本地源码编译 调试
下载nacos nacos在GitHub上有下载地址:https://github.com/alibaba/nacos/releases,可以选择任意版本下载。 我下载的是2.2.3 版本 导入idea mvn 安装包 1,切换到Terminal ,并且使用command prompt模式 2,执行 mvn -Prelease…...

WKB近似
WKB方法用于研究一种特定类型的微分方程的全局性质 很有用这种特定的微分方程形如: 经过一些不是特别复杂的推导,我们可以得到他的WKB近似解。 该近似解的选择取决于函数和参数的性质同时,我们默认函数的定义域为当恒大于零,时: 当…...
LeetCode算法二叉树—108. 将有序数组转换为二叉搜索树
目录 108. 将有序数组转换为二叉搜索树 代码: 运行结果: 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不…...

如何设置 Git 短命令
设置 Git 短命令 对喜欢敲命令而不用图形化工具的爱好者来说,设置短命令可以很好的提高效率。下面介绍两种设置短命令的方式。 方式一 git config --global alias.ps push方式二 打开全局配置文件 vim ~/.gitconfig写入内容 [alias] co checkoutps pushpl p…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
