C++ 2019-2022 CSP_J 复赛试题横向维度分析(中)
上文讲解了2019~2022年第一题和第二题。第一题偏数学认知,算法较简单,第二题考查基本数据结构,如队列、栈……和基础算法,如排序、模拟……。
本文继续讲解第三题和第四题。
1. 第三题
1.1 2022
题目:
逻辑表达式expr
问题描述:
逻辑表达式是计算机科学中的重要概念和工具,包含逻辑值、逻辑运算、逻辑运算优先级等内容。
在一个逻辑表达式中,元素的值只有两种可能:0(表示假)和1(表示真) 。元素之间有多种可能的逻辑运算,本题中只需考虑如下两种:“与”(符号为&)和“或"(符号为 |)。其运算规则如下 :
0 & 0 = 0 & 1 = 1 & 0 = 0,1&1=1;
0|0=0,0 | 1= 1 | 0 = 1 | 1=1。
在一个逻辑表达式中还可能有括号。规定在运算时,括号内的部分先运算;两种运算并列时,& 运算优先于|运算;同种运算并列时,从左向右运算。
比如,表达式0 | 1 & 0 的运算顺序等同于0 | ( 1 & 0 );表达式0 & 1 & 0 | 1的运算顺序等同于( ( 0 & 1 ) & 0 ) | 1。
此外,在 C++ 等语言的有些编译器中,对逻辑表达式的计算会采用一种“短路”的策略:在形如 a&b 的逻辑表达式中,会先计算a部分的值,如果a=0,那么整个逻辑表达式的值就一定为0,故无需再计算b部分的值;同理,在形如alb的逻辑表达式中,会先计算a部分的值如果a=1,那么整个逻辑表达式的值就一定为1,无需再计算b部分的值。
现在给你一个逻辑表达式,你需要计算出它的值,并且统计出在计算过程中,两种类型的“短路”各出现了多少次。需要注意的是,如某处“短路”包含在更外层被“短路”的部分内则不被统计,如表达式1 | ( 0 & 1 )中尽管0&1是一处“短路”,但由于外层的1 | ( 0 & 1 )本身就是一处“短路”,无需再计算0 & 1部分的值,因此不应当把这里的0 & 1计入一处“短路”。
分析问题:
此题考核前缀表达式、后缀表达式之间的关系。前缀表达式如何转换成后缀表达式,以及如何求解后缀表达式。如果对这两者很熟悉,此题拿下问题不大。问题除了需要得到最终结果,还需要求解短路的次数。所以结果是一个三元数组,当然也可以自定义结构体。
前缀表达式转后缀表达式时,需要使用栈,可以使用数组进行模拟或使用STL中的stack。
如果对此内容不是了解的,可以参考公众号里的相关文档。
编码实现:
#include <iostream>
#include <cmath>
using namespace std;
string s;
int stk1[1000005],stk2[1000005];//运算符栈和结果栈 (后缀表达式)
struct node {int v, cntand, cntor;
} stk3[1000005]; // 用来计算后缀表达式
int top1, top2, top3;
int priori(char x) { // 定义优先级if (x == '&') return 2;else if (x == '|') return 1;else if (x =='(') return 0;}
void makeSuf() { // 生成后缀表达式,即生成stk2数组for (int i = 0; i < s.size(); i ++) {if (s[i]=='(') {stk1[++top1] = s[i];} else if (s[i] ==')') {while (top1 > 0) {if (stk1[top1] =='(') break;stk2[++top2] = stk1[top1--];}top1--; // ( 自己也要出栈} else if (s[i] =='0' || s[i] =='1') {stk2[++top2] = s[i];} else {while (top1 > 0) {if (priori( stk1[top1]) >= priori(s[i])) {stk2[++top2] = stk1[top1--];} else break;}stk1[++top1] = s[i];}}while (top1 > 0)// 残留的运算符出栈stk2[++top2] = stk1[top1--];
}void calcSuf() {// 计算后缀表达式for (int i = 1; i <= top2; i++) {if (stk2[i] =='0' || stk2[i] =='1') { // 数字stk3[++top3] = (node) {stk2[i] -'0',0,0};} else if (stk2[i]=='&') { // &操作node y = stk3[top3--];node x = stk3[top3--]; // 注意x和y的顺序if (x.v == 0) { // 短路stk3[++top3] = (node) {0,x.cntand+1,x.cntor};} else {stk3[++top3] = (node) {y.v, x.cntand+y.cntand, x.cntor+y.cntor};}} else if (stk2[i] =='|') {// | 操作node y = stk3[top3--];node x = stk3[top3--];if (x.v == 1) { // 短路stk3[++top3] = (node) {1,x.cntand,x.cntor+1};} else {stk3[++top3] = (node) {y.v, x.cntand+y.cntand, x.cntor+y.cntor};}}}cout << stk3[1].v << endl;cout<< stk3[1].cntand <<" "<<stk3[1].cntor<< endl;
}int main() {cin >> s;makeSuf();// 生成后缀表达式calcSuf(); //计算后缀表达式return 0;
}
1.2 2021
题目:
网络连接
问题描述:
TCP/IP 协议是网络通信领域的一项重要协议。今天你的任务,就是尝试利用这个协议,还原一个简化后的网络连接场景。在本问题中,计算机分为两大类:服务机(Server)和客户机(client)。服务机负责建立连接,客户机负责加入连接。需要进行网络连接的计算机共有 n台,编号为 1~n,这些机器将按编号递增的顺 序,依次发起一条建立连接或加入连接的操作。每台机器在尝试建立或加入连接时需要提供一个地址串。服务机提供的地址串表示它尝试建立连接的地址,客户机提供的地址串表示它尝试加入连接的地址。 一个符合规范的地址串应当具有以下特征:
- 必须形如
a.b.c.d:e的格式,其中a,b,c,d,e均为非负整数; 0<a,b,cd<255,0<e65535;a,b,c,d,e均不能含有多余的前导0。
相应地,不符合规范的地址串可能具有以下特征:
- 不是形如
a.b.c.d:e格式的字符串,例如含有多于3个字符 . 或多于1个字符 : 等情况; - 整数
a,b,c, d,e中某一个或多个超出上述范围; - 整数
a,b,c,d,e中某一个或多个含有多余的前导0
例如,地址串 192.168.0.255:80 是符合规范的,但192.168.8.999:89 、192.168.0.1:1、192.168.0.1:088 、192:168::1.233 均是不符合规范的。
如果服务机或客户机在发起操作时提供的地址串不符合规范,这条操作将被直接忽略。在本问题中,我们假定凡是符合上述规范的地址串均可参与正常的连接,你无需考虑每个地址串的实际意义。 由于网络阻塞等原因,不允许两台服务机使用相同的地址串,如果此类现象发生, 后一台尝试建立连接的服务机将会无法成功建立连接,除此之外凡是提供符合规范的地址串的服务机均可成功建立连接。
如果某台提供符合规范的地址的客户机在尝试加入连接时,与先前某台已经成功建立连接的服务机提供的地址串相同,这台客户机就可以成功加入连接,并称其连接到这台服务机;如果找不到这样的服务机,则认为这台客户机无法成功加入连接。 请注意,尽管不允许两台不同的服务机使用相同的地址串,但多台客户机使用同样 的地址串,以及同一台服务机同时被多台客户机连接的情况是被允许的。 你的任务很简单:在给出每台计算机的类型以及地址串之后,判断这台计算机的连 接情况。
省略其它……
分析问题:
此题应该是史上最长文字描述了,如果对网络知识稍有一些认知的,其实题目很容易看性。服务机和客户机在建立连接时。服务机需要创建连接,监听连接。
客户机需要,发起连接,等待连接。需要此题篇幅较长,其实非常实现起来非常简单。
编码实现:
int n;int a[1005],b[1005],c[1005],d[1005],e[1005];
int good[1005]; // 服务器是否是好的
bool checkv(int i) { // 检查数值上合不合法
if (!(a[i] >= 0 && a[i] <= 255)) return false;
if (!(b[i]>= 0 && b[i] <= 255)) return false;
if (!(c[i] >= 0 && c[i] <= 255)) return false;
if (!(d[i] >= 0 && d[i] <= 255)) return false;
if (!(e[i] >= 0 && e[i] <= 65535)) return false;
return true;
}
bool deng(int i,int j) {//检查两个服务器是否完全重复
if (!(a[i] == a[j]))return false;
if (!(b[i] == b[j]))return false;
if (!(c[i]== c[j]))return false;
if (!(d[i]==d[j])) return false;
if (!(e[i] == e[j]))return false;
return true;
}
int main() {cin >> n;for (int i = 1; i <= n; i ++) {string type,,s;cin >> type >> s;int op;int err = 0;int cntdian = 0,cntmao = 0;for (int j = 0; j < s.size(); j ++) {if (s[j] =='.') cntdian ++;if (s[j]==':') cntmao ++;}if (cntdian == 3 && cntmao == 1) { S+=".";if (type == "Server") op = 1;else op = 2;string ss="";// 把.和: 之间的字符串记录下来 int cnt = 0;for(int j = 0;j<s.size();j++){if (s[j] =='.' || s[j] ==':'){if (cnt == 0 && (s[j]!='.')) err=1;if (cnt == 1 && (s[j] !='.')) err=1;if (cnt == 2 && (s[j] !='.')) err=1;if (cnt == 3 && (s[j] !='.')) err=1;if (ss == "") err = 1// 不能是空串if (ss[0] =='0'&& ss.size() != 1) {err = 1; // 检查有没有前导0}int v = 0; // 把ss字符串表示的数字计算出来for (int k = 0; k < ss.size(); k ++) {v = v * 10 + ss[k] -0';}cnt ++; // 第几个数字if (cnt == 1) a[i] = v;else if (cnt == 2) b[i] = v;else if (cnt == 3) c[i] = v;else if (cnt == 4)d[i] = v;else if(cnt == 5) e[i] = v;Ss ="";}else{ss += s[j];}}if (!checkv(i)) err = 1; // 检验合不合法}else{err = 1; // 如果不是有3个.以及1个: 也不合法}if (err == 1) {cout <<"ERR" << endl;continue;}if (op == 1){ // 服务器int ok = 1;for (int j= 1; j <= i-1; j ++) {if (good[j] == 1 & deng(i, j)) {ok = 0;break;}}if (ok == 0) {cout << "FAIL" << endl;} else{cout << "0k" << endl;good[i] = 1;}}else if (op == 2) // 客户机int ok = 0, id;for (int j= 1; j <= i-1; j ++) {if (good[j] == 1 && deng(i, j)) {ok = 1;id = j;break;}}if (ok == 0){cout << "FAIL" << endl;} else{cout << id << endl;}}
}
return 0;
}
1.3 2020
题目:
表达式(expr)
问题描述:
小C热衷于学习数理逻辑。有一天,他发现了一种特别的逻辑表达式。在这种逻辑表达式中,所有操作数都是变量,且它们的取值只能为0或1,运算从左往右进行。如果表达式中有括号,则先计算括号内的子表达式的值。特别的,这种表达式有且仅有以下几种运算:
与运算:a&b。当且仅当a和b的值都为1时,该表达式的值为1。其余情况该表达式的值为0。
或运算:a | b。当且仅当a和b的值都为0时,该表达式的值为0。其余情况该表达式的值为1。
取反运算:!a。当且仅当a的值为0时,该表达式的值为1。其余情况该表达式的值为0。
小C想知道,给定一个逻辑表达式和其中每一个操作数的初始取值后,再取反某一个操作数的值时,原表达式的值为多少。为了化简对表达式的处理,我们有如下约定:
表达式将采用后缓表达式的方式输入。
后缀表达式的定义如下:
如果E是一个操作数,则E的后缀表达式是它本身。
如果E是E1 op E2形式的表达式,其中op是任何二元操作符,且优先级不高于 E1、E2中括号外的操作符,则E的后缀式为E1'E2'op,其中E1'E2'分别为E1、E2的后缀式。
如果E是(E1)形式的表达式,则E1的后缀式就是E的后缀式。同时为了方便,输入中:
与运算符(&)、或运算符(|)、取反运算符(!)的左右均有一个空格,但表达式末尾没有空格。操作数由小写字母x与一个正整数拼接而成,正整数表示这个变量的下标。例如x10表示下标为10的变量x10。数据保证每个变量在表达式中出现恰好一次。
分析问题:
本质就是求解后缀表达式的结果,后缀表达式也是一棵二叉树,即可以按后缀表达式的特点求解,也可以构建一模二叉树后再求解。
编码实现:
#include <bits/stdc++.h> // c 头文件
#include <cstdio>
#include <algorithm>
using namespace std;int n,a[100],q;
int z[100],top;
int cnt;
struct tnode {int left,right,val;
};
tnode tree[100];
bool f[100];
bool change[100];bool dfs( int i ) {if( tree[i].val>=0 ) {f[i]=a[tree[i].val ];return f[i];}bool lval=dfs( tree[i].left );bool rval=dfs( tree[i].right );if( tree[i].val==-1 )f[i]=!lval;else if( tree[i].val==-2 )f[i]=lval & rval;else f[i]=lval | rval;return f[i];
}void result(int i) {if( tree[i].val>=0 ) {change[ tree[i].val ]=1;return;}if( tree[i].val==-1 )result( tree[i].left );else if( tree[ i ].val==-2 ) {if( f[tree[i].left]==1 && f[tree[i ].right]==1 ) {result( tree[i].left );result( tree[i].right );} else if( f[tree[i ].left]==0 && f[tree[i ].right]==1 ) {result( tree[i].left );} else if( f[tree[i ].left]==1 && f[tree[i ].right]==0 ) {result( tree[i].right );}} else {if( f[tree[i ].left]==0 && f[tree[i ].right]==0 ) {result( tree[i].left );result( tree[i].right );} else if( f[tree[i ].left]==0 && f[tree[i ].right]==1 ) {result( tree[i].right );} else if( f[tree[i ].left]==1 && f[tree[i ].right]==0 ) {result( tree[i].left );}}
}int main() {string s;getline(cin,s);int t=0;for(int i=0; s[i]; i++ ) {char ch=s[i];int val;if( ch=='x' ) {//数字++cnt;++t;tree[cnt].val=t;z[++top]=cnt;}//空格else if(ch==' ')continue;else {//运算符if( ch=='!' ) {++cnt;//一元运算符tree[cnt].left=z[top--];tree[cnt].val=-1;z[++top]=cnt;} else if(ch=='&') {++cnt;tree[cnt].left=z[top--];tree[cnt].right=z[top--];tree[cnt].val=-2;z[++top]=cnt;} else if(ch=='|') {++cnt;tree[cnt].left=z[top--];tree[cnt].right=z[top--];tree[cnt].val=-3;z[++top]=cnt;}}}cin>>n;for(int i=1; i<=n; i++) {cin>>a[i];}dfs(cnt );result(cnt);cin>>q;for(int i=1; i<=q; i++) {int x;cin>>x;if(change[x]) {cout<<!f[cnt]<<endl;} else {cout<<f[cnt]<<endl;}}return 0;
}
1.4 2019
题目:
纪念品
问题描述:
小伟突然获得一种超能力,他知道未米 T 天 N 种纪念品每天的价格。某个纪念品的价格是指购买一个该纪念品所需的金币数量,以及卖出一个该纪念品换回的金币数量。
每天,小伟可以进行以下两种交易无限次:
- 任选一个纪念品,若手上有足够金币,以当日价格购买该纪念品。
- 卖出持有的任意一个纪念品,以当日价格换回金币。
每天卖出纪念品换回的金币可以立即用于购买纪念品,当日购买的纪念品也可以当日卖出换回金币。当然,一直持有纪念品也是可以的。
T 天之后,小伟的超能力消失。因此他一定会在第 T 天卖出所有纪念品换回金币。
小伟现在有 M 枚金币,他想要在超能力消失后拥有尽可能多的金币。
分析问题:
这是一道完全背包的题,把今天手里的钱当做背包的容量,把商品今天的价格当成它的消耗,把商品明天的价格当做它的价值,
每一天结束后把总钱数加上今天赚的钱。
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j < bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
编码实现:
#include <iostream>
#include <memory.h>
using namespace std;
const int N = 101;
const int M = 10001;
int n, m, t, price[N][N], f[M];
int main() {cin >> t >> n >> m;//读入每种商品每天的价格for(int i = 1; i <= t; i++)for(int j = 1; j <= n; j++)cin >> price[j][i];//遍历天数for(int k = 1; k < t; k++) {memset(f, 0, sizeof f);//遍历物品for(int i = 1; i <= n; i++)//price[i][k] 第 i 件物品在第 k 天的价值for(int j = price[i][k]; j <= m; j++)//f[j] = max(f[j], f[j - price[i][k]] + price[i][k + 1] - price[i][k] );m += f[m];}cout << m;return 0;
}
1.5 小结
2021和2022的第三题是同性质的题,所以,认识前缀、后缀表达式,以及如何求解其表达式应该是重点也是难点知识。需要学生一定掌握。
3. 总结
从第三题开始,难度在逐步增加,需要有良好的算法和数据结构基础。
相关文章:
)
C++ 2019-2022 CSP_J 复赛试题横向维度分析(中)
上文讲解了2019~2022年第一题和第二题。第一题偏数学认知,算法较简单,第二题考查基本数据结构,如队列、栈……和基础算法,如排序、模拟……。 本文继续讲解第三题和第四题。 1. 第三题 1.1 2022 题目: 逻辑表达式…...
基于Spring Boot的IT技术交流和分享平台的设计与实现
目录 前言 一、技术栈 二、系统功能介绍 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 我国科学技术的不断发展,计算机的应用日渐成熟,其强大的功能给人们留下深刻的印象,它已经应用到了人类社会的各个层次的领域&#x…...

智算引领·创新未来 | 2023紫光展锐泛物联网终端生态论坛成功举办
9月21日,紫光展锐在深圳成功举办2023泛物联网终端生态论坛。论坛以“智算引领创新未来”为主题,吸引了来自信通院、中国联通、中国移动、中国电信、金融机构、终端厂商、模组厂商等行业各领域三百多位精英翘楚汇聚一堂,探讨在连接、算力驱动下…...

网络安全技术指南 103.91.209.X
网络安全技术指的是一系列防范网络攻击、保护网络安全的技术手段和措施,旨在保护网络的机密性、完整性和可用性。常见的网络安全技术包括: 防火墙:用于监控网络流量,过滤掉可能包括恶意软件的数据包。 加密技术:用于保…...
用flex实现grid布局
1. css代码 .flexColumn(columns, gutterSize) {display: flex;flex-flow: row wrap;margin: calc(gutterSize / -2);> div {flex: 0 0 calc(100% / columns);padding: calc(gutterSize / 2);box-sizing: border-box;} }2.用法 .grid-show-item3 {width: 100%;display: fl…...

东郊到家app小程序公众号软件开发预约同城服务系统成品源码部署
东郊到家app系统开发,东郊到家软件定制开发,东郊到家小程序APP开发,东郊到家源码定制开发,东郊到家模式系统定制开发 一、上门软件介绍 1、上门app是一家以推拿为主项,个人定制型的o2o平台,上门app平台提…...

kotlin的集合使用maxBy函数报NoSuchElementException
kotlin设定函数 fun test() {listOf<Int>().maxBy { it } } 查看java实现...
Python开发与应用实验2 | Python基础语法应用
*本文是博主对学校专业课Python各种实验的再整理与详解,除了代码部分和解析部分,一些题目还增加了拓展部分(⭐)。拓展部分不是实验报告中原有的内容,而是博主本人自己的补充,以方便大家额外学习、参考。 &a…...
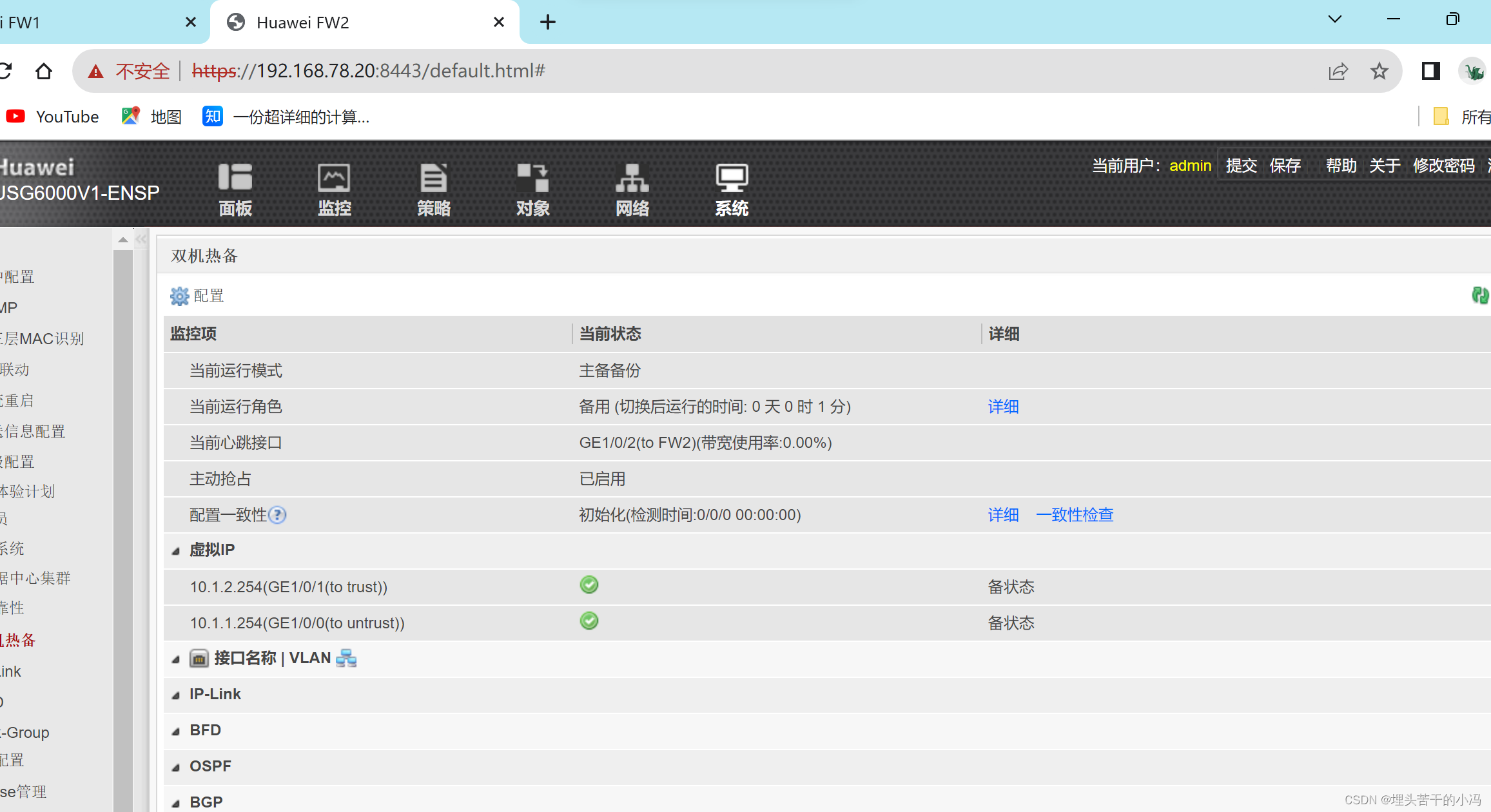
网络安全--防火墙旁挂部署方式和高可靠性技术
目录 一、防火墙 二、防火墙旁挂部署方式 使用策略路由实现 第一步、IP地址配置 第二步、配置路由 第三步、在防火墙上做策略 第四步、在R2上使用策略路由引流 三、防火墙高可靠性技术--HRP 拓扑图 第一步、配置SW1、SW2、FW1、FW2 第二步、进入防火墙Web页面进行配…...
)
c++最小步数模型(魔板)
C 最小步数模型通常用于寻找两个点之间的最短路径或最少步数。以下是一个基本的 C 最小步数模型的示例代码: #include<bits/stdc.h> using namespace std; const int N 1e5 5; vector<int> G[N]; int d[N]; bool vis[N];void bfs(int s) {queue<i…...

【每日一题Day337】LC460LFU 缓存 | 双链表+哈希表
LFU 缓存【LC460】 请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。 实现 LFUCache 类: LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象int get(int key) - 如果键 key 存在于缓存中,则获取键的值&#x…...
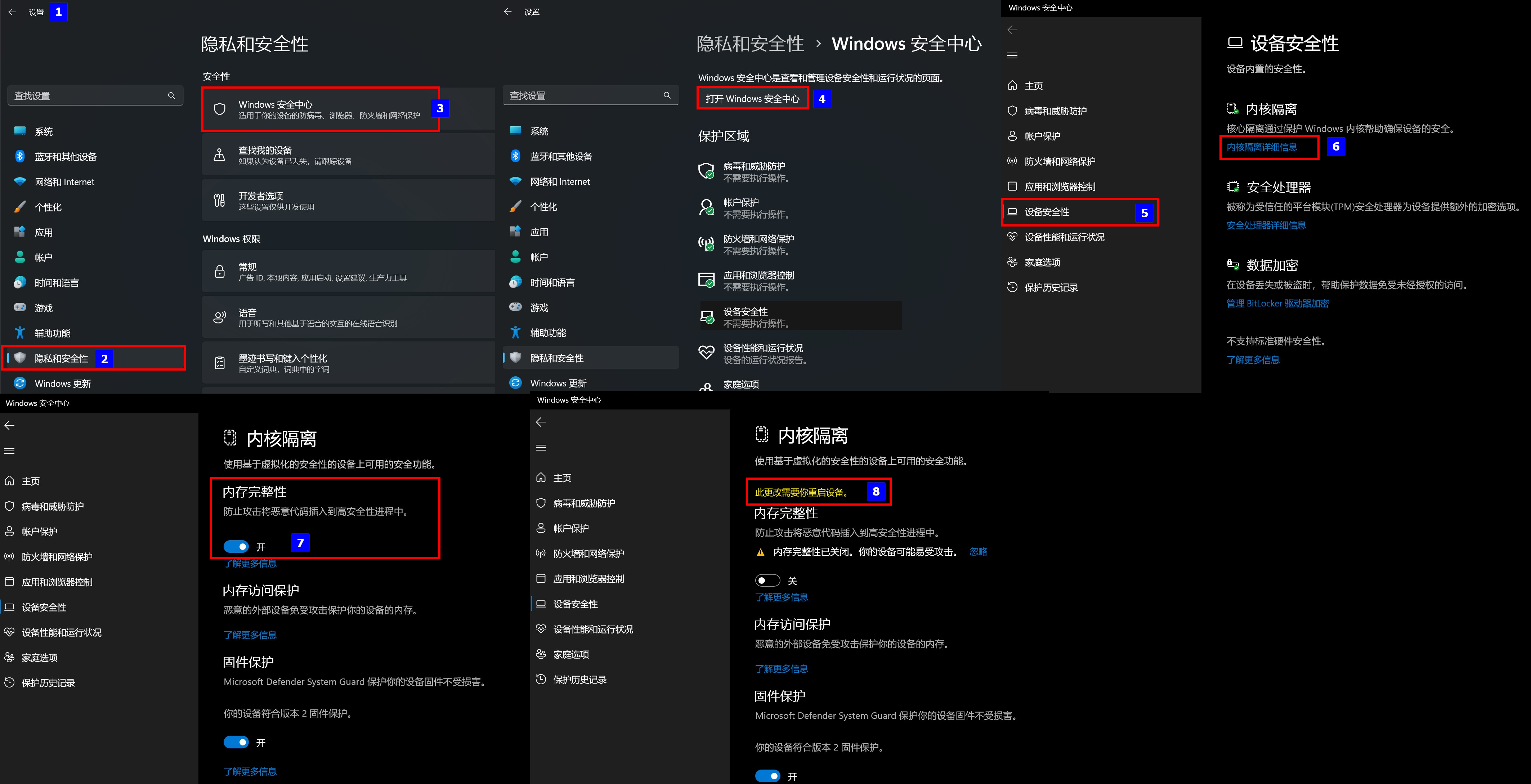
解决老版本Oracle VirtualBox 此应用无法在此设备上运行问题
问题现象 安装华为eNSP模拟器的时候,对应的Oracle VirtualBox-5.2.26安装的时候提示兼容性问题,无法进行安装,具体版本信息如下: 软件对应版本备注Windows 11专业工作站版22H222621eNSP1.3.00.100 V100R003C00 SPC100终结正式版…...

法规标准-UN R48标准解读
UN R48是做什么的? UN R48全名为关于安装照明和灯光标志装置的车辆认证的统一规定,主要描述了对各类灯具的布置要求及性能要求;其中涉及自动驾驶功能的仅有6.25章节【后方碰撞预警信号】,因此本文仅对此章节进行解读 功能要求 …...

自动化和数字化在 ERP 系统中意味着什么?
毋庸置疑,ERP系统的作用是让工作更轻松。它可以集成流程,提供关键分析,确保你的企业高效运营。这些信息可以提高你的运营效率,并将有限的人力资本重新部署到更有效、更重要的需求上。事实上,自动化和数字化是ERP系统最…...

python nvidia 显卡信息 格式数据
python nvidia 显卡信息 格式数据. def get_gpu_memory():result subprocess.check_output([nvidia-smi, --query-gpupci.bus_id,memory.used,memory.total,memory.free, --formatcsv])# 返回 GPU 的显存使用情况,单位为 Minfo []for t in csv.DictReader(result…...
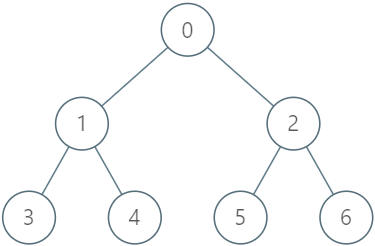
LeetCode每日一题:1993. 树上的操作(2023.9.23 C++)
目录 1993. 树上的操作 题目描述: 实现代码与解析: 模拟 dfs 原理思路: 1993. 树上的操作 题目描述: 给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 p…...

绿色计算产业发展白皮书:2022年OceanBase助力蚂蚁集团减排4392tCO2e
9 月 15 日,绿色计算产业联盟在 2023 世界计算大会期间重磅发布了《绿色计算产业发展白皮书(2023 版)》。蚂蚁集团作为指导单位之一,联合参与了该白皮书的撰写。 白皮书中指出,落实“双碳”战略,绿色计算已…...

阿里云通义千问14B模型开源!性能超越Llama2等同等尺寸模型
9月25日,阿里云开源通义千问140亿参数模型Qwen-14B及其对话模型Qwen-14B-Chat,免费可商用。Qwen-14B在多个权威评测中超越同等规模模型,部分指标甚至接近Llama2-70B。阿里云此前开源了70亿参数模型Qwen-7B等,一个多月下载量破100万࿰…...

两横一纵 | 寅家科技发布10年新征程战略
2023年9月22日,寅家科技“寅路向前”10年新征程战略发布会在上海举办,来自投资领域的东方富海、深创投、高新投等知名投资机构,一汽大众、一汽红旗、奇瑞汽车等主机厂,国家新能源汽车技术创新中心、梅克朗、芯驰科技、思特威等合作…...

二值贝叶斯滤波计算4d毫米波聚类目标动静属性
机器人学中有些问题是二值问题,对于这种二值问题的概率评估问题可以用二值贝叶斯滤波器binary Bayes filter来解决的。比如机器人前方有一个门,机器人想判断这个门是开是关。这个二值状态是固定的,并不会随着测量数据变量的改变而改变。就像门…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
