二叉树的存储
目录
1.使用孩子表示法创建二叉树
2.二叉树的遍历
2.1前中后序遍历
2.2 前中后序遍历的选择题
2.3实现前中后序遍历
2.3.1前序遍历
2.3.2中序遍历
2.3.3后序遍历
3.二叉树的基本操作
3.1获取叶子节点的个数
3.2获取树中节点的个数
3.3获取第K层节点的个数
3.4获取二叉树的高度
3.5检测值为value的元素是否存在
1.使用孩子表示法创建二叉树
这篇文章主讲的是链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式。
二叉表示:
// 孩子表示法class Node {int val ; // 数据域Node left ; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right ; // 右孩子的引用,常常代表右孩子为根的整棵右子树}
三叉表示:
// 孩子双亲表示法class Node {int val ; // 数据域Node left ; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right ; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent ; // 当前节点的根节点}
这篇文章使用的存储储存方式是孩子表示法
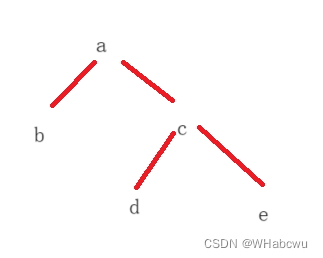
在学习二叉树的基本操作前,需先要手动快速创建一棵简单的二叉树,使用孩子表示法。创建如下(图1)二叉树。
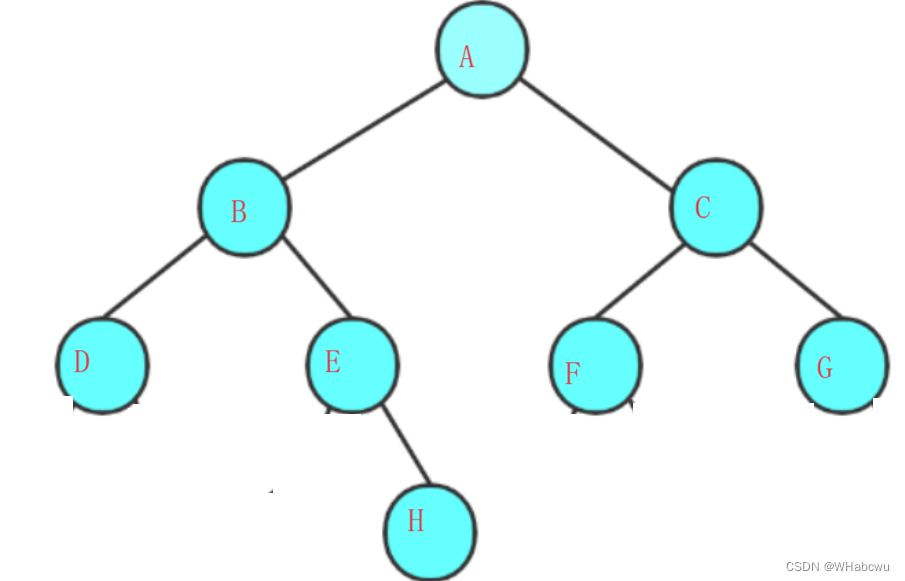
public class Tree {class TreeNode{char val;TreeNode left;TreeNode right;public TreeNode(char val){this.val=val;}}public TreeNode create(){TreeNode A=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode C=new TreeNode('C');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');TreeNode H=new TreeNode('H');A.left=B;A.right=C;B.left=D;B.right=E;C.left=F;C.right=G;E.right=H;return A;}
}
2.二叉树的遍历
2.1前中后序遍历
为什么要有前中后序遍历顺序?
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱, 如果按 照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的
NLR :前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点 ---> 根的左子树 ---> 根的右子树。LNR :中序遍历 (Inorder Traversal)—— 根的左子树 ---> 根节点 ---> 根的右子树。LRN :后序遍历 (Postorder Traversal)—— 根的左子树 ---> 根的右子树 ---> 根节点。
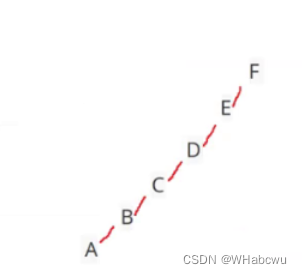
以图一为例:
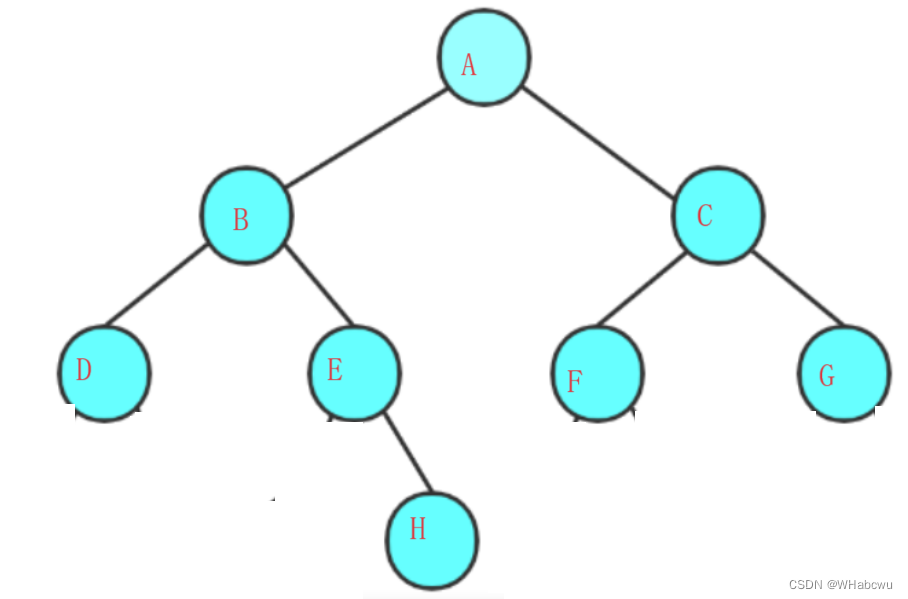
前序遍历结果:A B D E H C F G中序遍历结果:D B E H A F C G后序遍历结果:D H E B F G C A
2.2 前中后序遍历的选择题
(1)某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
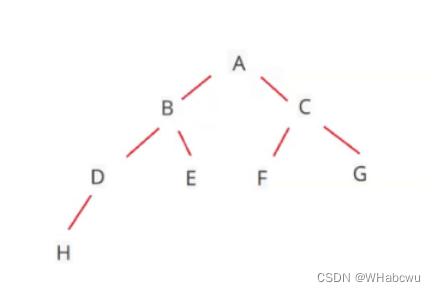
故选A
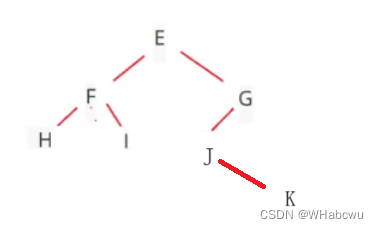
(2) 二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()

2.3实现前中后序遍历
2.3.1前序遍历
// 前序遍历void preOrder(TreeNode root){if(root==null){return;}System.out.println(root.val+" ");preOrder(root.left);preOrder(root.right);}2.3.2中序遍历
// 中序遍历void inOrder(TreeNode root){if(root==null){return;}preOrder(root.left);System.out.println(root.val+" ");preOrder(root.right);}2.3.3后序遍历
// 后序遍历void postOrder(TreeNode root){if(root==null){return;}preOrder(root.left);preOrder(root.right);System.out.println(root.val+" ");}
3.二叉树的基本操作
// 获取树中节点的个数int size ( Node root );// 获取叶子节点的个数int getLeafNodeCount ( Node root );// 获取第 K 层节点的个数int getKLevelNodeCount ( Node root , int k );// 获取二叉树的高度int getHeight ( Node root );// 检测值为 value 的元素是否存在Node fifind ( Node root , int val );
3.1获取叶子节点的个数
当前节点的左右子树若都为空,说明该节点为叶子结点,返回1
树的叶子节点的个数=左树叶子节点的个数+右树叶子节点的个数
int getLeafNodeCount(TreeNode root){if(root==null){return 0;}return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);}3.2获取树中节点的个数
若当前结点为空,返回0
先获取左节点个数,再获取右节点个数,然后返回两者相加再加上根节点的个数1
int size(TreeNode root){if(root==null){return 0;}return size(root.right)+size(root.left)+1;}3.3获取第K层节点的个数
本质是计算k=1时的节点数
树的叶子第K层节点的个数=左树叶子第K-1层节点的个数+右树第K-1层节点的个数
int getKLevelNodeCount(TreeNode root, int k) {if(root==null){return 0;}if(k==1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}3.4获取二叉树的高度
![]()
int getHeight(TreeNode root) {if(root==null){return 0;}int lefthight=getHeight(root.left);int rifhthight=getHeight(root.right);return lefthight>rifhthight?(lefthight+1):(rifhthight+1);}3.5检测值为value的元素是否存在
遍历左(右)子树,若没有找到,则返回null,若找到,则返回该结点
TreeNode fifind(TreeNode root, int val) {if (root==null){return null;}if(root.val==val){return root;}TreeNode lefttree=fifind(root.left, val);if(lefttree!=null){return lefttree;}TreeNode righttree=fifind(root.right, val);if(righttree!=null){return righttree;}return null;}以上为我个人的小分享,如有问题,欢迎讨论!!!
都看到这了,不如关注一下,给个免费的赞 ![]()

相关文章:

二叉树的存储
目录 1.使用孩子表示法创建二叉树 2.二叉树的遍历 2.1前中后序遍历 2.2 前中后序遍历的选择题 2.3实现前中后序遍历 2.3.1前序遍历 2.3.2中序遍历 2.3.3后序遍历 3.二叉树的基本操作 3.1获取叶子节点的个数 3.2获取树中节点的个数 3.3获取第K层节点的个数 3.4获取…...

List 去重的几种方法
🔔HashSet去重 import java.util.HashSet;HashSet<Integer> set new HashSet<>(); set.add(1); set.add(2); set.add(2); System.out.println(set); // [1, 2]🔔TreeSet去重 import java.util.TreeSet;TreeSet<Integer> set new T…...

UNet网络制作
UNet网络制作 代码参考UNet数据集制作及代码实现_哔哩哔哩_bilibili,根据该UP主的代码,加上我的个人整理和理解。(这个UP主的代码感觉很好,很规范 UNet网络由三部分组成:卷积块,下采样层,上采样…...

智能热水器丨打造智能家居新体验
随着科学技术的不断发展,智能电器越来越被大众所采纳,如智能扫地机,智能洗衣机,智能微波炉等等,越来越智能的电器为人们的生活带来了许多便利。以往的热水器一般都是只有按键/机械的控制方式,没有其他无线控…...
)
Python 十进制转化二进制1.0(简易版)
"""十进制转换二进制知识点:1、循环语句/跳转语句 while/break2、运算符 求余%、整除//3、字符串拼接4、字符串切片5、数据类型转换不足与改善:1、不能输入非正整数,否则报错或卡住"""# 倒序二进制存储 revers…...

WebGL 选中一个表面
目录 选中一个表面 示例程序(PickFace.js) 代码详解 gl.readPixels()见126行效果 gl.UNSIGNED_BYTE注意点 示例效果 选中一个表面 WebGL 选中物体_山楂树の的博客-CSDN博客可以使用同样的方法来选中物体的某一个表面。这一节在Pi…...
open ai chartgpt 安装插件 txyz.ai
1 chatgpt 页面 左下角 用户 -> setting 2 3...

【算法思想】贪心
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

freeswitch-01
文章目录 1. 电话实现技术2. 模拟信号与数字信号2.1 模拟信号2.2 数字信号 3. PCM4. 局间中继与电路复用技术5. 信令5.1 定义5.2 分类5.2.1 功能分类5.2.2 工作区域分类5.2.3 信道分类 5.3 用户线信令5.4 局间信令5.5 七号信令5.6 H.323与SIP信令 6. 媒体6.1 定义 7. 电路交换与…...
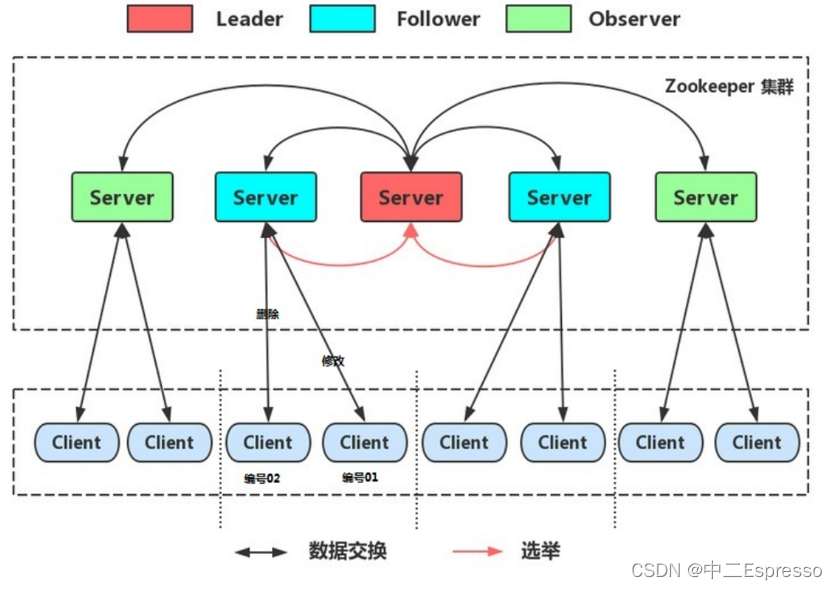
Zookeeper-集群介绍与核心理论
Zookeeper集群 4.Zookeeper集群4.1) 介绍4.2) 核心理论 4.Zookeeper集群 4.1) 介绍 Leader选举: Serverid:服务器ID。比如有三台服务器,编号分别是1,2,3。编号越大在选择算法中的权重越大。Zxid:数据ID。服务器中存放的最大数据…...

动态分配的内存位置在哪里?
在C++中,动态分配的内存位于称为堆(Heap)的内存区域。以下是一些关于堆和其他相关内存区域的基本信息: 堆(Heap): 这是一个用于动态内存分配的内存区域。使用new(C++)或malloc(C)等函数从堆中分配内存,并使用delete(C++)或free(C)释放这些内存。堆的大小通常受…...

Vue3中的Ref与Reactive:深入理解响应式编程
前言 Vue 3是一个功能强大的前端框架,它引入了一些令人兴奋的新特性,其中最引人注目的是ref和reactive。这两个API是Vue 3中响应式编程的核心,本文将深入探讨它们的用法和差异。 什么是响应式编程? 在Vue中,响应式编…...
Windows10/11显示文件扩展名 修改文件后缀名教程
前言 写这篇文章的原因是由于我分享的教程中的文件、安装包基本都是存在阿里云盘的,下载后需要改后缀名才能使用。 但是好多同学不会改。。 Windows 10 随便打开一个文件夹,在上方工具栏点击 “查看”点击 “查看” 后下方会显示更详细的工具栏然后点…...

【C++】手撕string(string的模拟实现)
手撕string目录: 一、 Member functions 1.1 constructor 1.2 Copy constructor(代码重构:传统写法和现代写法) 1.3 operator(代码重构:现代写法超级牛逼) 1.4 destructor 二、Other mem…...

用python3编译cv_bridge
文章目录 概要依赖工作空间编译可能遇到的问题error: option --install-layout not recognized概要 当我在编写一个使用传感器图像传输和OpenCV4的ROS包时,从构建到编译代码的一切都很顺利。当我开始运行节点本身时,问题出现了,它给出了以下错误: Assertion failed (tlsSl…...

招商信诺人寿基于 Apache Doris 统一 OLAP 技术栈实践
本文导读: 当前,大数据、人工智能、云计算等技术应用正在推动保险科技发展,加速保险行业数字化进程。在这一背景下,招商信诺不断探索如何将多元数据融合扩充,以赋能代理人掌握更加详实的用户线索,并将智能…...

我的python安装在哪儿了?python安装路径怎么查?
对于 Python 开发者来说,Windows 系统中的 Python 安装路径是非常重要的。在本文中,我们将从多个方面探究如何查看 Python 安装路径,并提供代码示例。 一、使用文件浏览器查看 Python 安装路径 在 Windows 系统中,我们可以使用文…...

视频汇聚/安防监控平台EasyCVR指定到新的硬盘进行存储录像,如何自动挂载该磁盘?
TSINGSEE青犀视频监控汇聚平台EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安防视频监控的能力&…...

读博时的建议或心得
https://www.zhihu.com/question/32210068/answer/264273093 读论文:一开始读论文,一定要读顶会顶刊的,以后也一直要这样。如此,一方面保持了研究的水准,时刻提醒自己:我就是混这个层次的。另一方面&#…...

3分钟,免费制作一个炫酷实用的数据可视化大屏!
在当前大数据时代背景下,数据已成为在工业革命中如同煤炭、石油一般宝贵的资源。但是由于数据越来越庞大、越来越复杂,导致数据的可读性也越来越低。因此,对数据可视化的需求也越来越高,需要解决的问题也越来越复杂,而…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
