想要精通算法和SQL的成长之路 - 最长递增子序列 II(线段树的运用)
想要精通算法和SQL的成长之路 - 最长递增子序列 II(线段树的运用)
- 前言
- 一. 最长递增子序列 II
- 1.1 向下递推
- 1.2 向上递推
- 1.3 更新操作
- 1.4 查询操作
- 1.5 完整代码:
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 最长递增子序列 II
原题链接

在做这个题目之前,先看一下:数据结构 - 线段树的运用 。
在线段树的基础上,思路如下:
- 首先,题目要求了子序列中,相邻的元素差不能超过
k值。我们假设线段树的val值,存储的就是最长递增子序列的长度。 - 我们定义
query函数的返回就是范围区间内的最长递增子序列长度。
那么伪代码就是:
public int lengthOfLIS(int[] nums, int k) {int ans = 0;for (int i = 0; i < nums.length; i++) {int tmp = query(nums[i]);ans = Math.max(ans, tmp);}return ans;
}
但是有一个问题:假设我们以num[i]作为最后一个元素,但是我并不知道它的前一个元素是谁。那咋办?
结合线段树的一个区间求值性质,我们只要求得区间 [num[i] - k, num[i] - 1] 之间的最长子序列长度,再加上1(当前子序列的最后一个元素num[i]),那么就可以求得以num[i]为结尾的最长子序列长度了。
同时我们还要更新各个子区间对应的最长长度,即伪代码:
for (int i = 0; i < nums.length; i++) {int tmp = query(nums[i]);update(tmp)ans = Math.max(ans, tmp);
}
1.1 向下递推
我们做更新操作的时候,求得不再是 数据结构 - 线段树的运用 里面的区间和,而是最大值。因此我们不能在原本值的基础上做加减法运算。而是做覆盖运算。
class Node {Node left, right;int val, add;
}private void pushDown(Node node) {if (node.left == null) {node.left = new Node();}if (node.right == null) {node.right = new Node();}if (node.add == 0) {return;}node.left.val = node.add; // 替换node.right.val = node.add; // 替换node.left.add = node.add; // 替换node.right.add = node.add; // 替换node.add = 0;
}
1.2 向上递推
求以当前节点作为最长子序列的最后一个元素时的序列长度时,我们可以拿到:
- 左子序列的最长递增长度。
- 右子序列的最长递增长度。
两者取最大,那么代码就是:
private void pushUp(Node node) {node.val = Math.max(node.left.val, node.right.val);
}
1.3 更新操作
public void update(Node node, int start, int end, int left, int right, int val) {// 如果线段树的区间完全在查询区间内,那么直接更新当前节点的 val 值即可if (start >= left && end <= right) {// 覆盖旧值node.val = val;// 覆盖需要传递的节点值node.add = val;return;}// 如果不在查询区间内,那么我们需要递归更新左右子树int mid = (start + end) >> 1;// 向下传递标记pushDown(node);if (left <= mid) {update(node.left, start, mid, left, right, val);}// [mid + 1, end] 和 [l, r] 可能有交集,遍历右孩子区间if (right > mid) {update(node.right, mid + 1, end, left, right, val);}// 计算当前节点的val值pushUp(node);
}
1.4 查询操作
public int query(Node node, int start, int end, int left, int right) {// 若当前区间完全在查询区间内,直接返回当前区间的最值if (left <= start && end <= right) {return node.val;}// 把当前区间 [start, end] 均分得到左右孩子的区间范围int mid = (start + end) >> 1, ans = 0;// 下推标记pushDown(node);// [start, mid] 和 [l, r] 可能有交集,遍历左孩子区间if (left <= mid) {ans = query(node.left, start, mid, left, right);}// [mid + 1, end] 和 [l, r] 可能有交集,遍历右孩子区间if (right > mid) {ans = Math.max(ans, query(node.right, mid + 1, end, left, right));}return ans;
}
1.5 完整代码:
有个问题就是:我们在遍历数组的每个元素num[i]的时候,我们的线段树区间应该设置为多少?
因为我们是以每个元素的 [num[i] - k, num[i] - 1]区间来做计算的,因此线段树的范围和num[i]的范围有关系。
题目有个提示:

那么确定好了线段树的区间范围,我们可以编写代码如下:
class Solution {public int lengthOfLIS(int[] nums, int k) {int ans = 0;Node root = new Node();for (int i = 0; i < nums.length; i++) {// 查询区间 [nums[i] - k, nums[i] - 1] 区间范围内的,以每个元素为末尾元素时的最长递增子序列长度。int cnt = query(root, 0, N, Math.max(0, nums[i] - k), nums[i] - 1) + 1;// 更新,注意这里是覆盖更新,对应的模版中覆盖更新不需要累加,已在下方代码中标注update(root, 0, N, nums[i], nums[i], cnt);ans = Math.max(ans, cnt);}return ans;}class Node {Node left, right;int val, add;}private int N = (int) 1e5;private Node root = new Node();public void update(Node node, int start, int end, int left, int right, int val) {// 如果线段树的区间完全在查询区间内,那么直接更新当前节点的 val 值即可if (start >= left && end <= right) {// 覆盖旧值node.val = val;// 覆盖需要传递的节点值node.add = val;return;}// 如果不在查询区间内,那么我们需要递归更新左右子树int mid = (start + end) >> 1;// 向下传递标记pushDown(node);if (left <= mid) {update(node.left, start, mid, left, right, val);}// [mid + 1, end] 和 [l, r] 可能有交集,遍历右孩子区间if (right > mid) {update(node.right, mid + 1, end, left, right, val);}// 计算当前节点的val值pushUp(node);}public int query(Node node, int start, int end, int left, int right) {// 若当前区间完全在查询区间内,直接返回当前区间的最值if (left <= start && end <= right) {return node.val;}// 把当前区间 [start, end] 均分得到左右孩子的区间范围int mid = (start + end) >> 1, ans = 0;// 下推标记pushDown(node);// [start, mid] 和 [l, r] 可能有交集,遍历左孩子区间if (left <= mid) {ans = query(node.left, start, mid, left, right);}// [mid + 1, end] 和 [l, r] 可能有交集,遍历右孩子区间if (right > mid) {ans = Math.max(ans, query(node.right, mid + 1, end, left, right));}return ans;}private void pushUp(Node node) {node.val = Math.max(node.left.val, node.right.val);}private void pushDown(Node node) {if (node.left == null) {node.left = new Node();}if (node.right == null) {node.right = new Node();}if (node.add == 0) {return;}node.left.add = node.add; // 不需要累加node.right.add = node.add; // 不需要累加node.left.val = node.add; // 不需要累加node.right.val = node.add; // 不需要累加node.add = 0;}
}
相关文章:

想要精通算法和SQL的成长之路 - 最长递增子序列 II(线段树的运用)
想要精通算法和SQL的成长之路 - 最长递增子序列 II(线段树的运用) 前言一. 最长递增子序列 II1.1 向下递推1.2 向上递推1.3 更新操作1.4 查询操作1.5 完整代码: 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长递增子序列 II 原题链接…...

java用easyexcel按模版导出
首先在项目的resources下面建一个template包,之后在下面创建一个模版,模版格式如下: 名称为 financeReportBillStandardTemplateExcel.xlsx: {.fee}类型的属性值,是下面实体类的属性,要注意这里面的格式&a…...
Servlet执行流程生命周期方法介绍体系结构、Request和Response的功能详解
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Servlet 一、 Servlet执行流程二、Servlet生…...
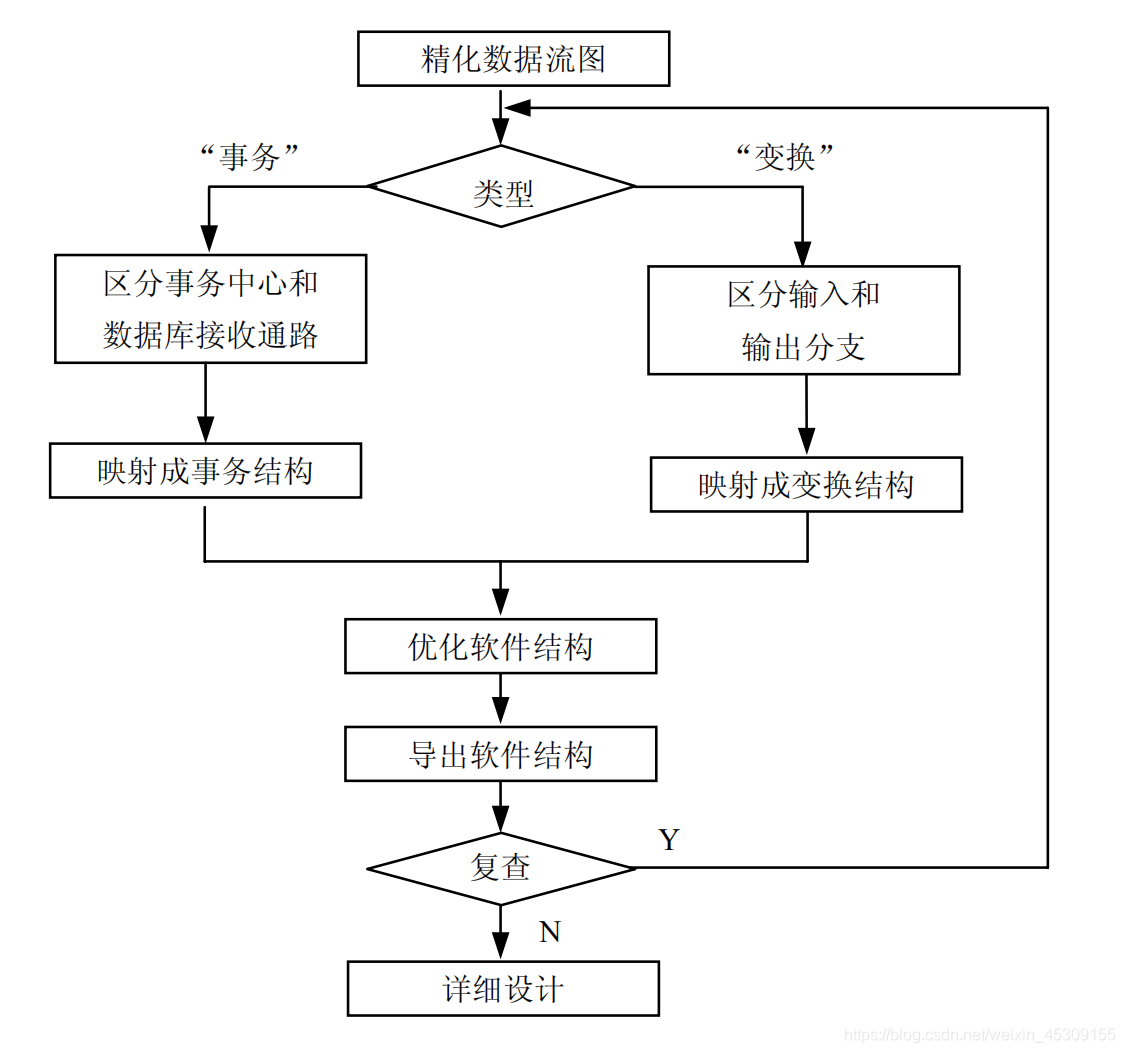
软件工程之总体设计
总体设计是软件工程中的一个重要阶段,它关注整个系统的结构和组织,旨在将系统需求转化为可执行的软件解决方案。总体设计决定了系统的架构、模块划分、功能组织以及数据流和控制流等关键方面。 可行性研究 具体方面:经济可行性、技术可行性…...

监控员工电脑文件拷贝记录:电脑怎么看员工复制文件的历史记录
在现代企业管理中,数据安全和保密是极其重要的一环。企业需要确保敏感信息不被泄露,以防止可能的法律纠纷和经济损失。为此,许多公司都采取了一些措施来监控员工的电脑使用行为。其中,监控文件拷贝记录是一种常见的方法。本文将详…...
文件通用下载方法封装)
vue中request.js中axios请求和(若依)文件通用下载方法封装
vue中request.js中axios请求和(若依)文件通用下载方法封装 1.request.js import axios from axios import { Message, Loading } from element-ui import { saveAs } from file-saver // 创建axios实例 const request axios.create({// 这里可以放一…...
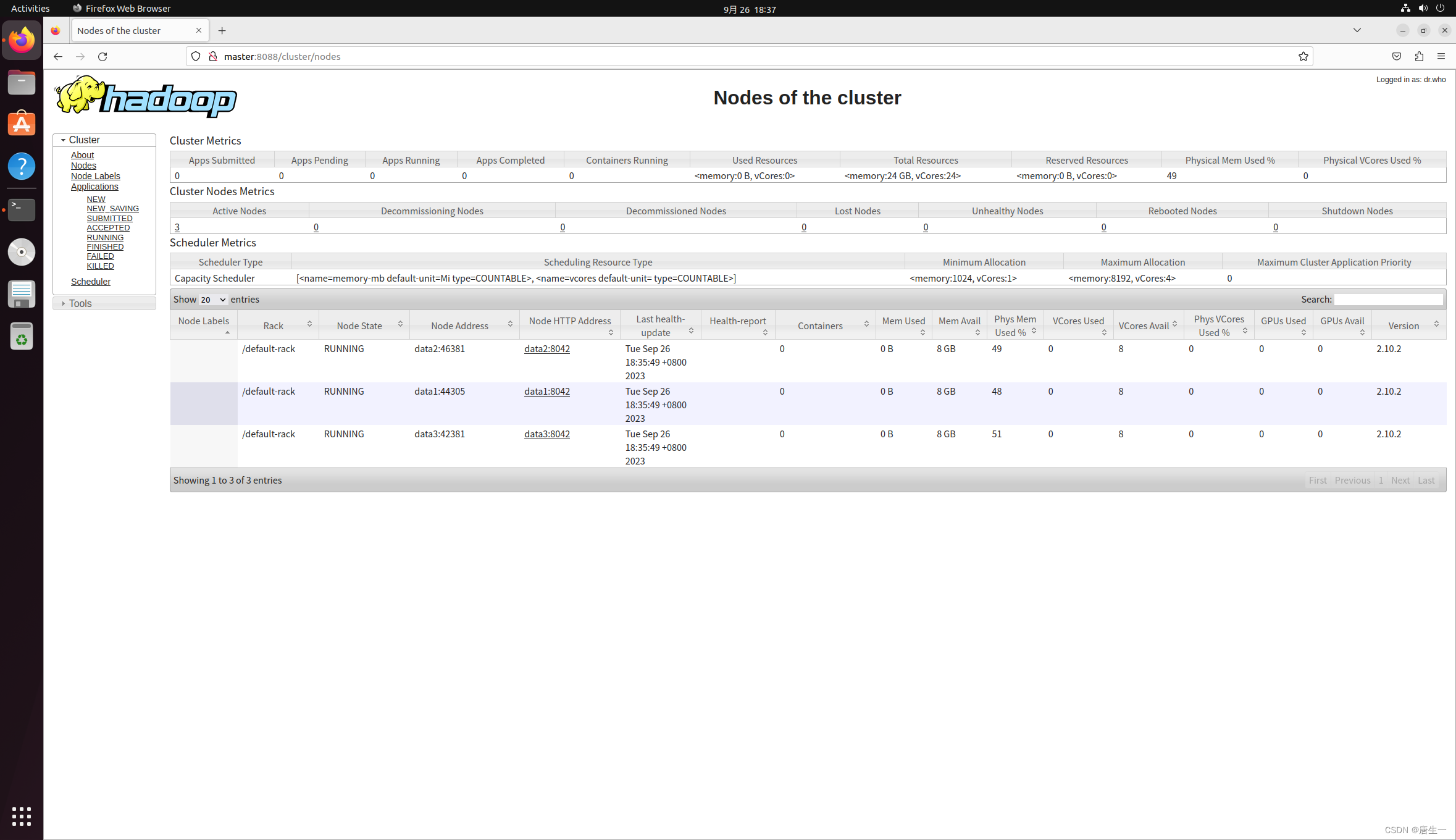
【大数据存储与处理】1. hadoop单机伪分布安装和集群安装
0. 写在前面 0.1 软件版本 hadoop2.10.2 ubuntu20.04 openjdk-8-jdk 0.2 hadoop介绍 Hadoop是一个由Apache基金会所开发的分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。充分利用集群的威力进行高速运算和存储。Hadoop实现了一个…...

linux通过time命令统计代码编译时间
首先编写一个编译脚本 build.sh 内容如下: 然后执行time sh build.sh 编译完成后输出三个时间 time sh xxx.sh # 会返回3个时间数据 (1) real:从进程 ls 开始执行到完成所耗费的 CPU 总时间。该时间包括 ls 进程执行时实际使用的 CPU 时间,…...

logback日志是怎么保证多线程输出日志线程安全的
logback中的单例模式 logback日志框架使用了单例设计模式来进行日志输出。在logback中,Logger类是一个关键的组件,它负责记录和输出日志消息。 Logger类使用了单例设计模式,确保在一个应用程序中只存在一个Logger实例。这样做的好处是可以确…...

2022年统计用区划代码表SQL 01
行政区划代码为国家公布的六位县级以上行政区划代码 行政区编码的用途: APP里做城市级联选择根据身份证前六位获取用户所在城市区县 370786 昌邑市 370800 济宁市 370811 任城区 370812 兖州区 百度高德等接口通常都会返回adcode字段 (行政区编码)根据 行政区编…...

EM@基本初等函数@幂和根式@指数函数
abstract 基本初等函数幂和根式指数函数 指数和幂 正整指数幂 a n a^{n} an a ⋯ a ⏟ n 个 \underbrace{a\cdots{a}}_{n个} n个 a⋯a, n ∈ N n\in\mathbb{N^{}} n∈N 其中 a n a^{n} an称为** a a a的 n n n次幂** a a a叫做幂的底数, n n n叫做幂的指数 正整指数…...

时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测
时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测 目录 时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测&#…...

element 二次确认框,内容自定义处理
上代码: async inspectionTypeOff(row) {console.log(row.id);let taskArray await this.getTaskList(row.id); // 查询关联的任务console.log("taskArray", taskArray);let messageTip taskArray.length > 0? <div><p>确认禁用巡检项&…...

【软件设计师-中级——刷题记录4(纯干货)】
目录 进度管理工具Grantt图:程序语言基础:高级语言源程序模式: 每日一言:持续更新中... 个人昵称:lxw-pro 个人主页:欢迎关注 我的主页 个人感悟: “失败乃成功之母”,这是不变的道理…...

9.24 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表 1、自动驾驶一周资讯 - 小马智行在京开展“车内无人”出行服务商业化试点,余承东将升任车BU董事长 自动驾驶一周资讯 - 小马智行在京开展“车内无人”出行服务商业化试点࿰…...
持续更新)
第二章:25+ Python 数据操作教程(第二十五节用 PYTHON 和 R 制作祝福圣诞节)持续更新
这篇文章献给所有 Python 和 R 编程爱好者...通过以下程序在同行中炫耀您的知识。作为一名数据科学专业人士,您希望自己的愿望在圣诞节前夕变得特别。如果您观察代码,您还可以学到 1-2 个技巧,您可以在以后的日常任务中使用这些技巧。 方法 1:运行以下程序,看看我的意思 R…...
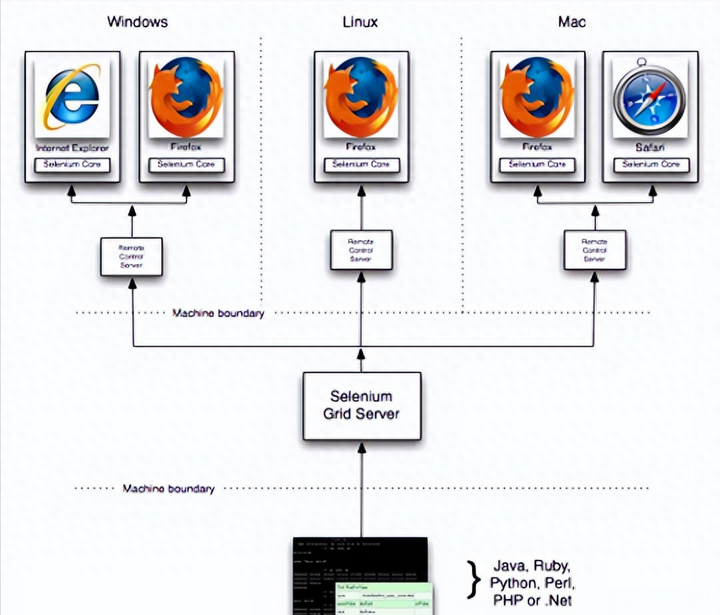
你是怎么理解自动化测试的?理解自动化测试的目的和本质
其实自动化测试很好理解,由两部分组成,“自动化”和“测试”,所以我们要理解自动化测试,就必须理解“自动化”和“测试”,只有理解了这些概念,才能更轻松的做好的自动化测试。其中“自动化”可以想象成通过…...

二十六、MySQL并发事务问题:脏读/不可重复读/幻读
1、事务的隔离级别 (1)隔离级别 Read uncommitted # 读,未提交 Read committed # 读,已提交 Repeatable Read(默认) # 可重复读 Serializable # 串读 (2)基础语法 set transaction isolation level 事…...

RK3588平台开发系列讲解(项目篇)视频监控之RTMP推流
文章目录 一、RTMP协议是什么二、RTMP 的原理三、Nginx 流媒体服务器四、FFmpeg 推流沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 目前常见的视频监控和视频直播都是使用了 RTMP、RTSP、HLS、MPEG-DASH、WebRTC流媒体传输协议等。 视频监控项目组成,分为三部分:…...
http基础教程(超详细)
HTTP HTTP 一 、基础概念 请求和响应报文URL 二、HTTP 方法 GETHEADPOSTPUTPATCHDELETEOPTIONSCONNECTTRACE 三、HTTP 状态码 1XX 信息2XX 成功3XX 重定向4XX 客户端错误5XX 服务器错误 四、HTTP 首部 通用首部字段请求首部字段响应首部字段实体首部字段 五、具体应用 连接管理…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
