【高阶数据结构】红黑树(C++实现)
⭐博客主页:️CS semi主页
⭐欢迎关注:点赞收藏+留言
⭐系列专栏:C++进阶
⭐代码仓库:C++进阶
家人们更新不易,你们的点赞和关注对我而言十分重要,友友们麻烦多多点赞+关注,你们的支持是我创作最大的动力,欢迎友友们私信提问,家人们不要忘记点赞收藏+关注哦!!!
【高阶数据结构】红黑树
- 一、红黑树的概念
- 二、红黑树的性质
- 三、红黑树结点的定义
- 四、红黑树结点的插入
- 对红黑树是否需要调整,怎么调整?
- 情况一、插入的叔叔结点存在且为红色
- 情况二、插入的叔叔结点存在且为黑色
- 一条直线型
- 折线
- 情况三、插入结点的叔叔结点不存在
- 一条直线型
- 折线
- 代码操作
- 五、验证是否是红黑树
- 六、红黑树的高度
- 七、红黑树的查找
- 八、红黑树的删除
- (一)情况一
- (二)情况二
- 1、brother为红色
- 2、brother为黑色,且其左右孩子都是黑色结点或为空
- 3、brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空
- 4、brother为黑色,且其右孩子是红色结点
- (三)右边子树
- (四)情况说明
- (五)删除操作
- 代码
- 九、红黑树与AVL树的比较
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。
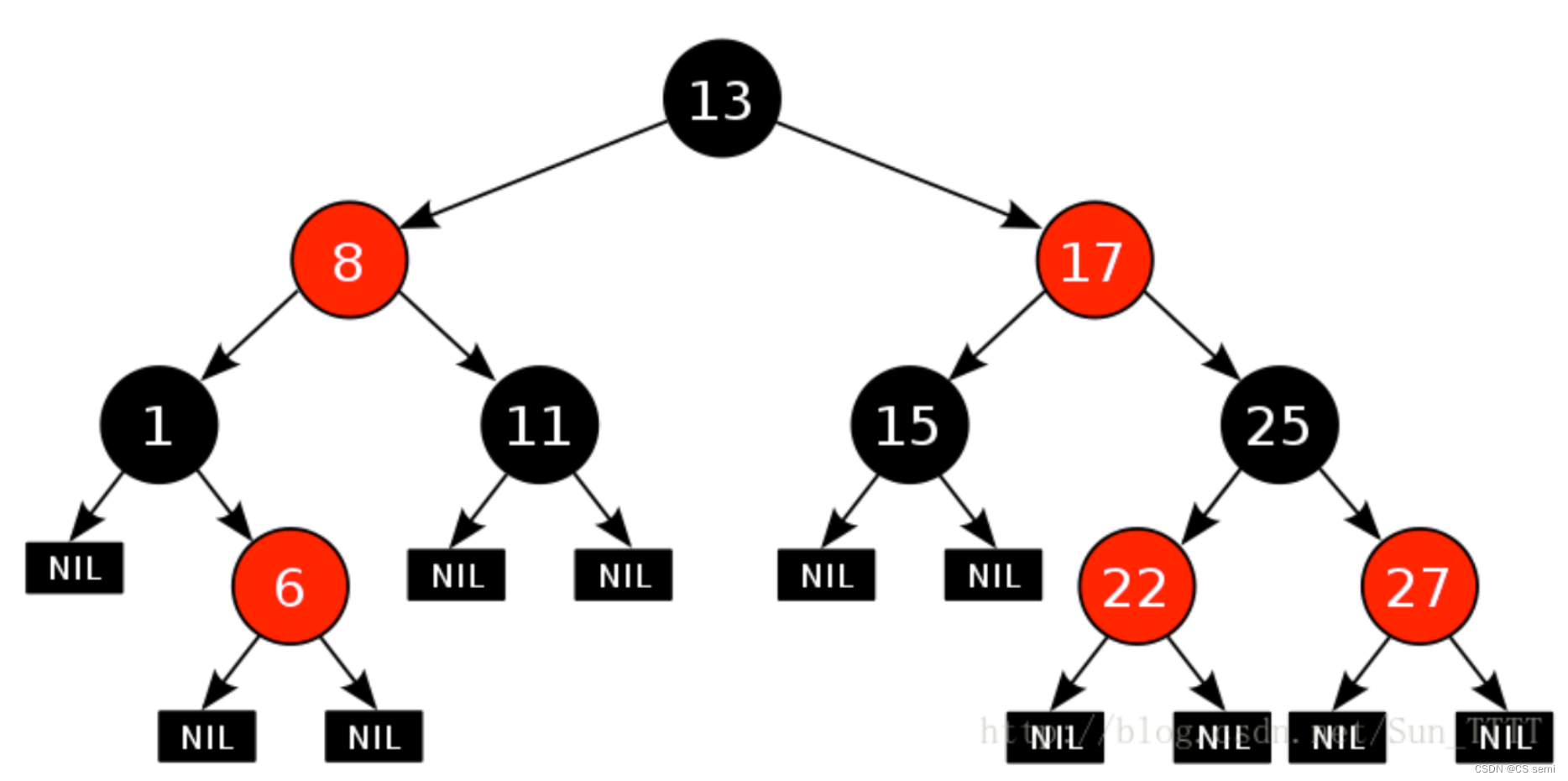
二、红黑树的性质
红黑树的五大性质:
1、每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
我们需要思考一个问题:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
根据性质三,说明红节点后必定是黑节点,红黑树中不可能出现连续的红色结点,再根据性质四,说明在每个结点的后代结点的简单路径上均包含相同数目的黑色结点。
假如我们假设有N个黑色结点,那么最短路径就是全部由黑色结点构成的路径,其长度为N。
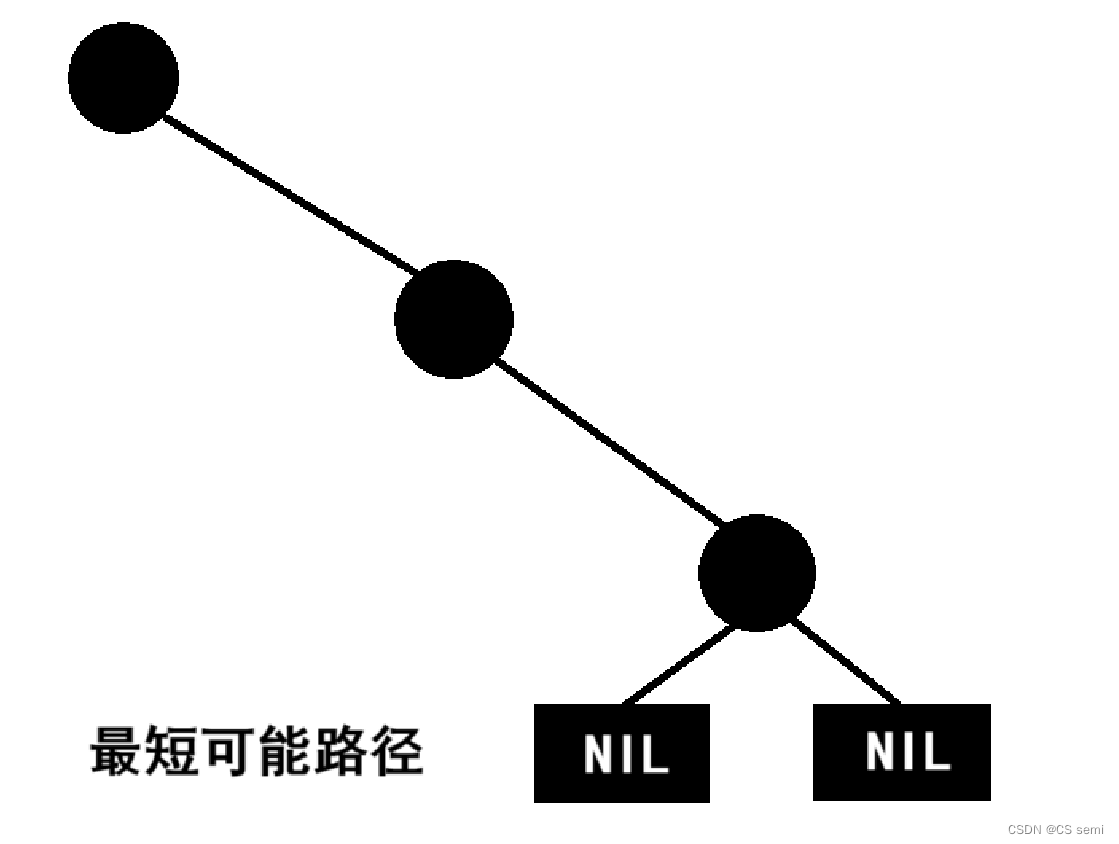
最长可能路径是一黑一红间隔往下排列,所以总长度为2N。

所以红黑树从根到叶子的最长可能路径不超过最短可能路径的2倍。
三、红黑树结点的定义
我们定义了一个K-V的模型的红黑树。为了方便后续的旋转操作,我们将红黑树的结点定义为三叉链的结构,我们还加入了一个定义结点颜色的枚举类型,表示结点的颜色。
// 定义结点颜色
enum Col
{RED,BLACK
};// 定义红黑树结点
template<class K, class V>
struct RBTreeNode
{// 构造函数RBTreeNode(const pair<K, V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED),_kv(kv){}// 三叉链RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;// 存储颜色int _col;// 存储键值对pair<K, V> _kv;
};
四、红黑树结点的插入
插入之前我们先思考一个简单的问题,每次插入插入什么颜色的结点呢?
答案是红色结点,为什么呢?
因为我们假如插入的是黑色结点,发现,这条路径下的黑色结点比别的路径下的黑色结点多了一个,就会违背性质四,所以就需要调整黑色结点和红色结点,调整的结点数有可能是全部,而加入说我们插入的是红色结点,这条路上的黑色结点是没有增加的,而且其他路的黑色结点也都是没有增加的,所以是平衡的,但有一种情况是其父节点是红色的,插入的是红色结点就会导致连续的红色结点,即违背了性质三,所以也是需要调整的,我们在下面进行总结:
1、插入黑色结点:失误点在于必然导致这一条路径下黑色结点增多,违背性质四,必须要调整颜色。
2、插入红色结点:失误点在于可能其父节点为红色,需要调整,但如果其父节点本来就是黑色那就不需要调整。
所以,我们在根据权衡利弊后,决定需要插入红色结点。
插入过程:(三段步骤,和AVL树的插入整体思路大致相同)
1、找:根据二叉搜索树的插入方法,找到待插入位置。
2、插:将待插入结点插入到树中。
3、调:若插入结点的父结点是红色的,则需要对红黑树进行调整。
对红黑树是否需要调整,怎么调整?
并不是所有的红黑树都需要调整,有一种情况是需要调整的结点的父节点为黑色结点,我们插入红色的结点并不会对本树有影响,所以这种情况是不需要进行调整的。
所以,只有插入结点的父节点为红色结点才需要进行调整的,因为这样会出现连续的红色结点,此时也说明了其父节点绝对不是根节点,因为性质二是根节点(root)是黑色的,所以其插入结点的祖父结点一定存在,此时,红黑树的调整需要判断父节点的兄弟结点,即叔叔结点,所以根据叔叔结点来判断一下不同的情况:
情况一、插入的叔叔结点存在且为红色
为了保持没有连续的红色结点,我们可以将父节点变黑,因为要保证每一条路径的黑色结点是一样的,所以就需要将叔叔节点也变成黑色的。同样也解决了红色结点连续的问题。
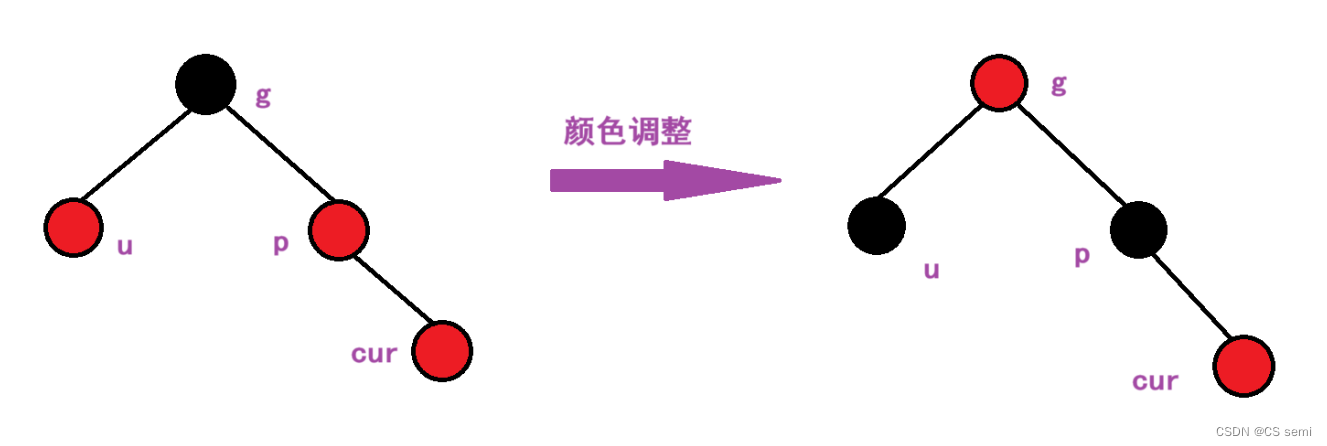
但此时调整并没有完,因为我们不确定祖父节点是不是整个红黑树的根节点,所以就需要进行判断:
如果祖父节点是根节点,我们仅需要将组父节点变成黑色的即可,也就是每条路上多增加了一个黑色结点,不影响。
而如果祖父节点不是根节点,我们就需要继续往上判断,判断祖父的父节点的颜色,再根据这些进行判断叔叔节点。
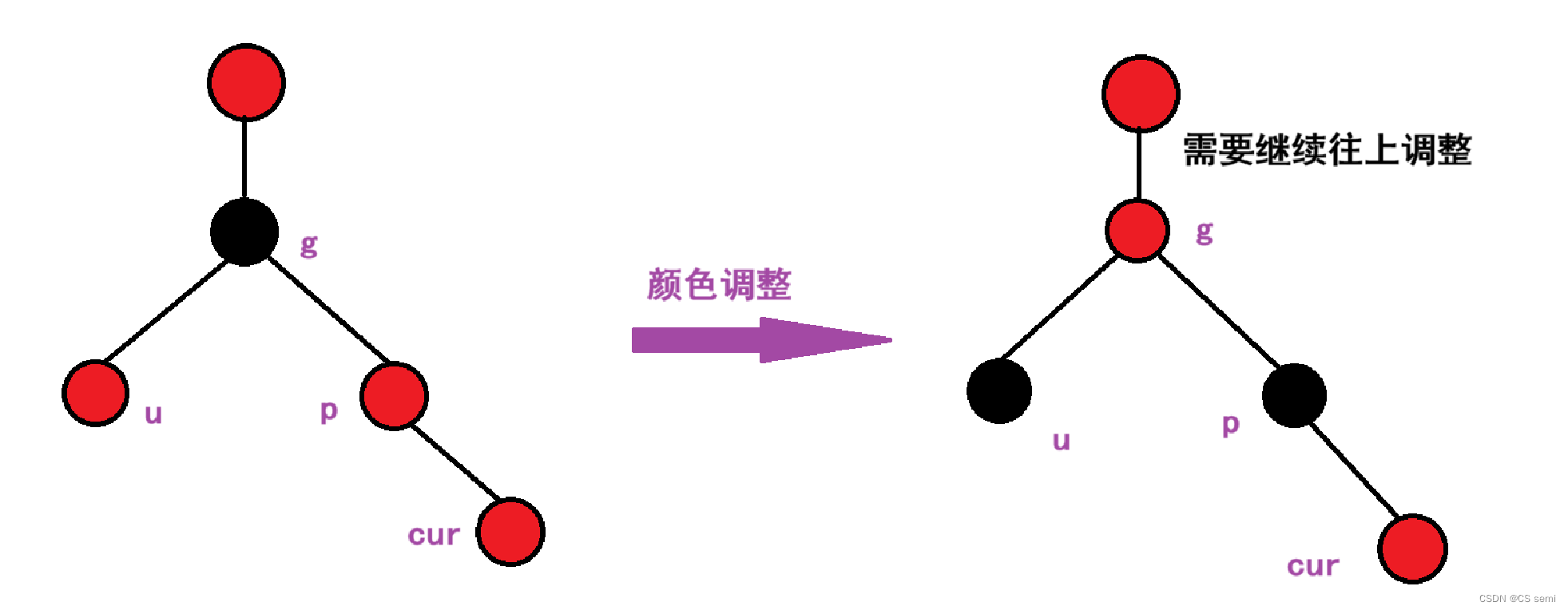
此时不管cur在父节点的左孩子还是右孩子,其调整都是一样的。
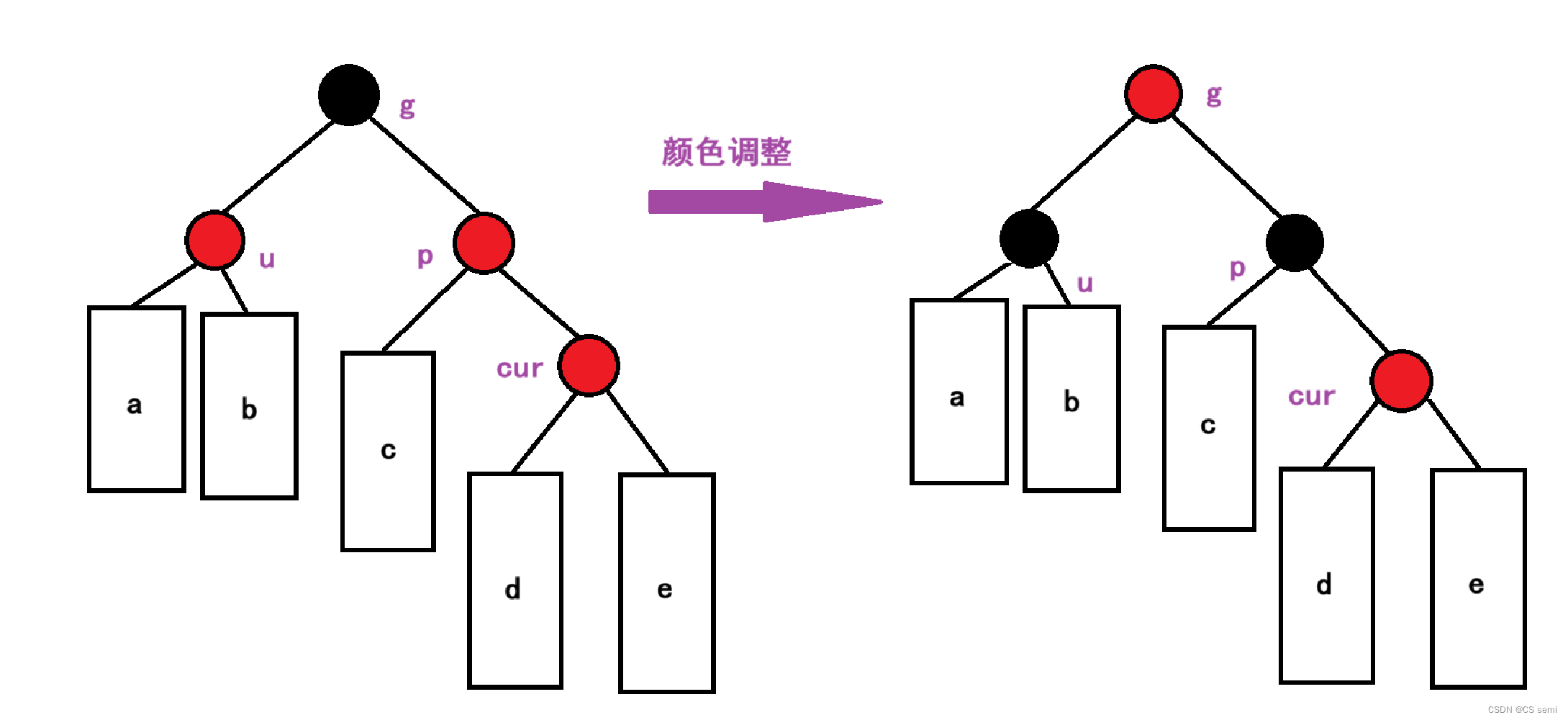
情况二、插入的叔叔结点存在且为黑色
这种情况我们可以进行具体的分析一下,我们画张图表示:
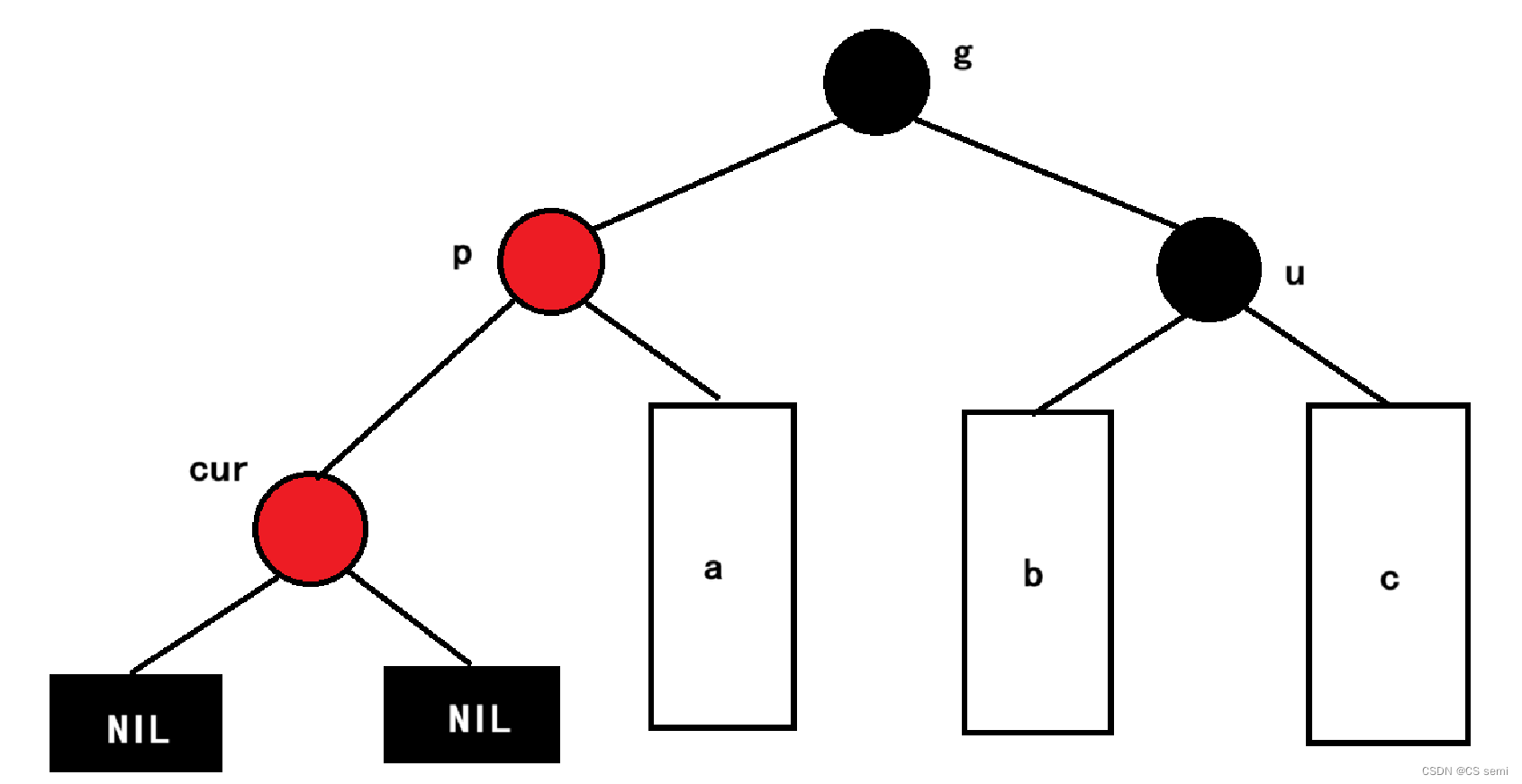
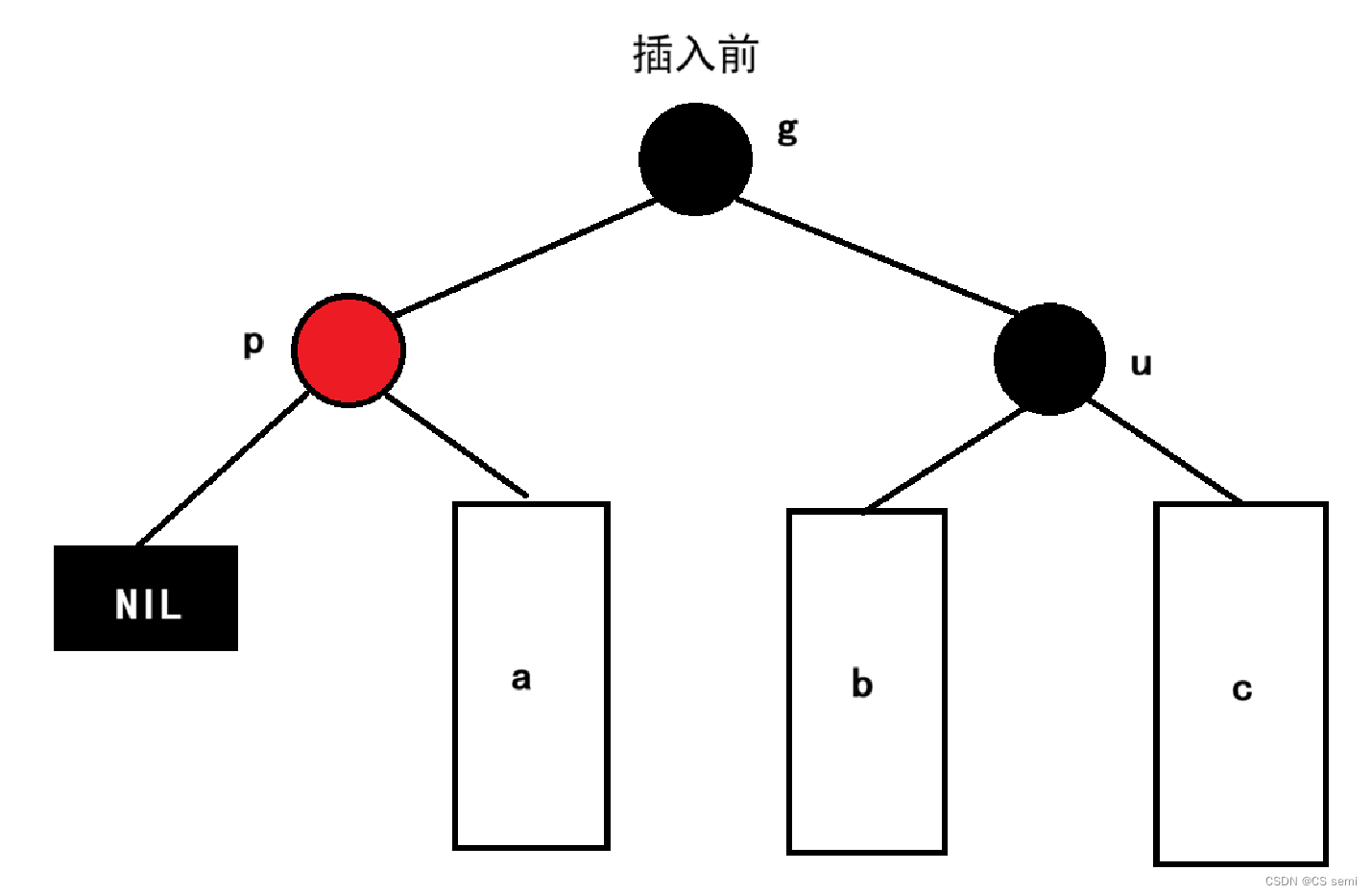
我们插入的话是这样的,但是不知道大家有没有发现一个错误,这我们不是说每条路径下黑色节点是一样的吗?我们假设组父节点g之上的黑色结点数为x个,叔叔结点之下的黑色节点为y个,则在插入cur之前,我们的左右两边的黑色结点数分别为:x+1(路径一直到NIL空结点)和x+y+2。明显右子树的黑色结点多,根本不满足红黑树的要求!所以这个插入情况肯定不是在新插入时候的情况,而是在情况一往上进行更新的过程中存在的。
注意小贴士:
1、我们算黑色结点是需要算到空的,也就是我们的NIL结点,不是到叶子结点结束,而是算到它下面的空结点。
2、出现这种情况我们单纯靠变色是肯定不行的,所以就需要我们进行像AVL树的旋转操作,而旋转操作以后是不需要继续往上调整了。
两种情况:
一条直线型
仅用单旋(左旋或者是右旋),我们这里列举一种情况(用右单旋–p在g的左孩子,cur在p的左孩子):
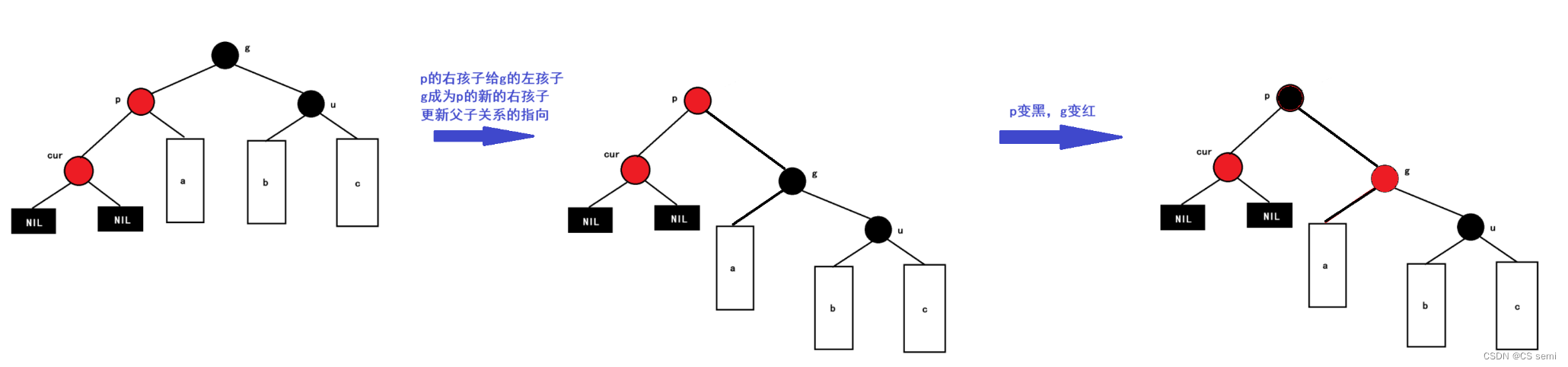
左单旋的情况是p在g的右孩子,cur在p的右孩子。
折线
若cur,p,g这三个结点成为一条折线的情况下,需要进行双旋操作再进行变色处理,我们这里讲解一下左右双旋,即先左单旋再右单旋,我们画个抽象图:
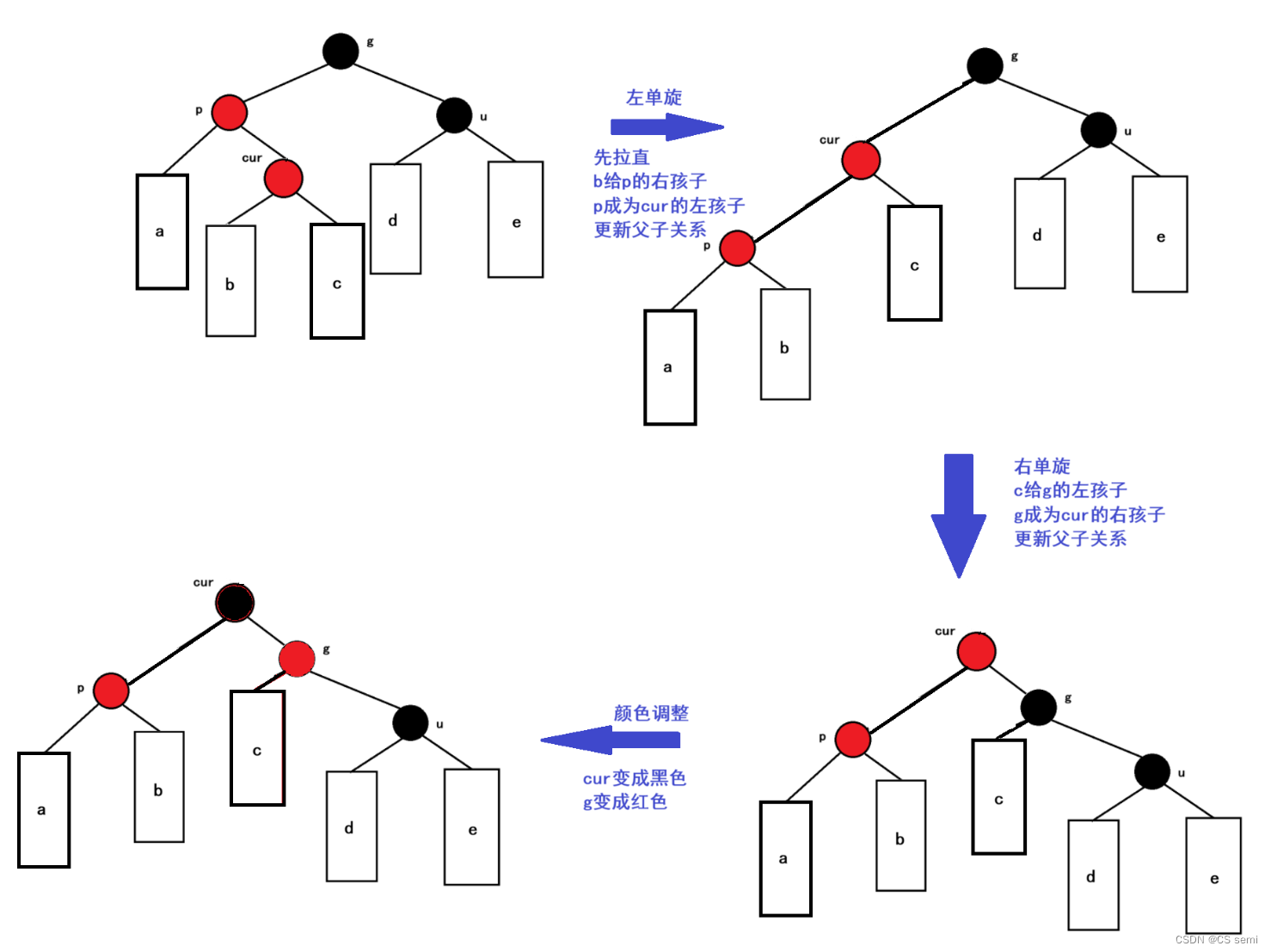
当p是g的右孩子,cur是p的左孩子的时候,用的是右左双旋。
情况三、插入结点的叔叔结点不存在
我们还是分析一下,这个结点cur是否是新插入的结点?我们先来画一张图来解决一下:
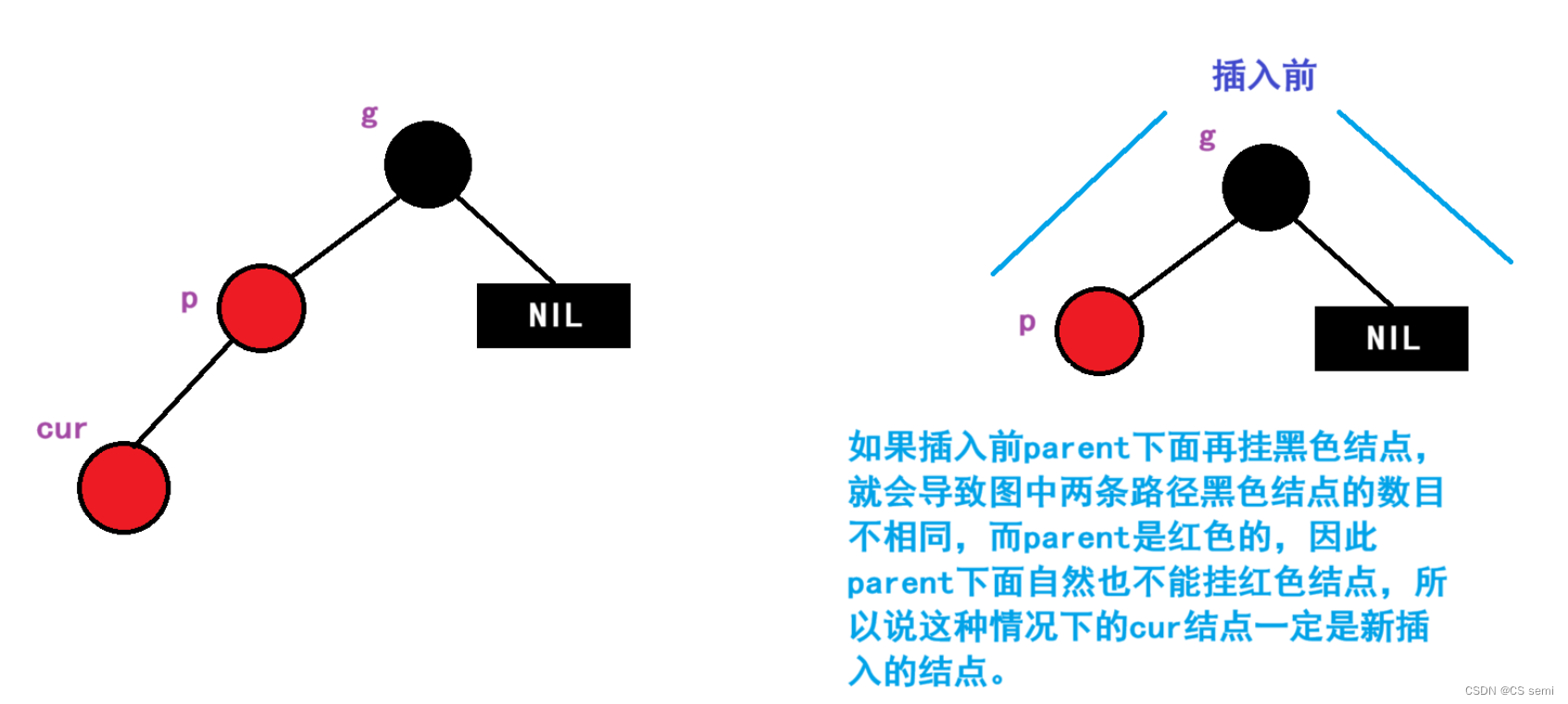
一条直线型
我们下面图是使用右单旋:
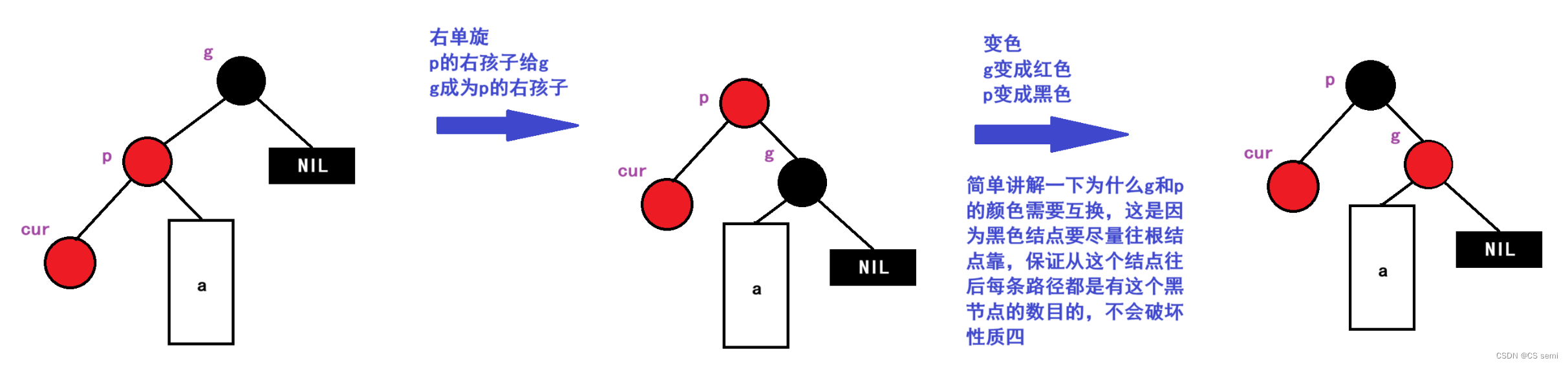
当p是g的右孩子,cur也是p的右孩子的时候,我们使用的是左单旋,之后再进行变色处理即可。
折线
当cur、p、g三个结点成为一条折线的时候,是需要进行双旋的,我们下面使用的是左右双旋:
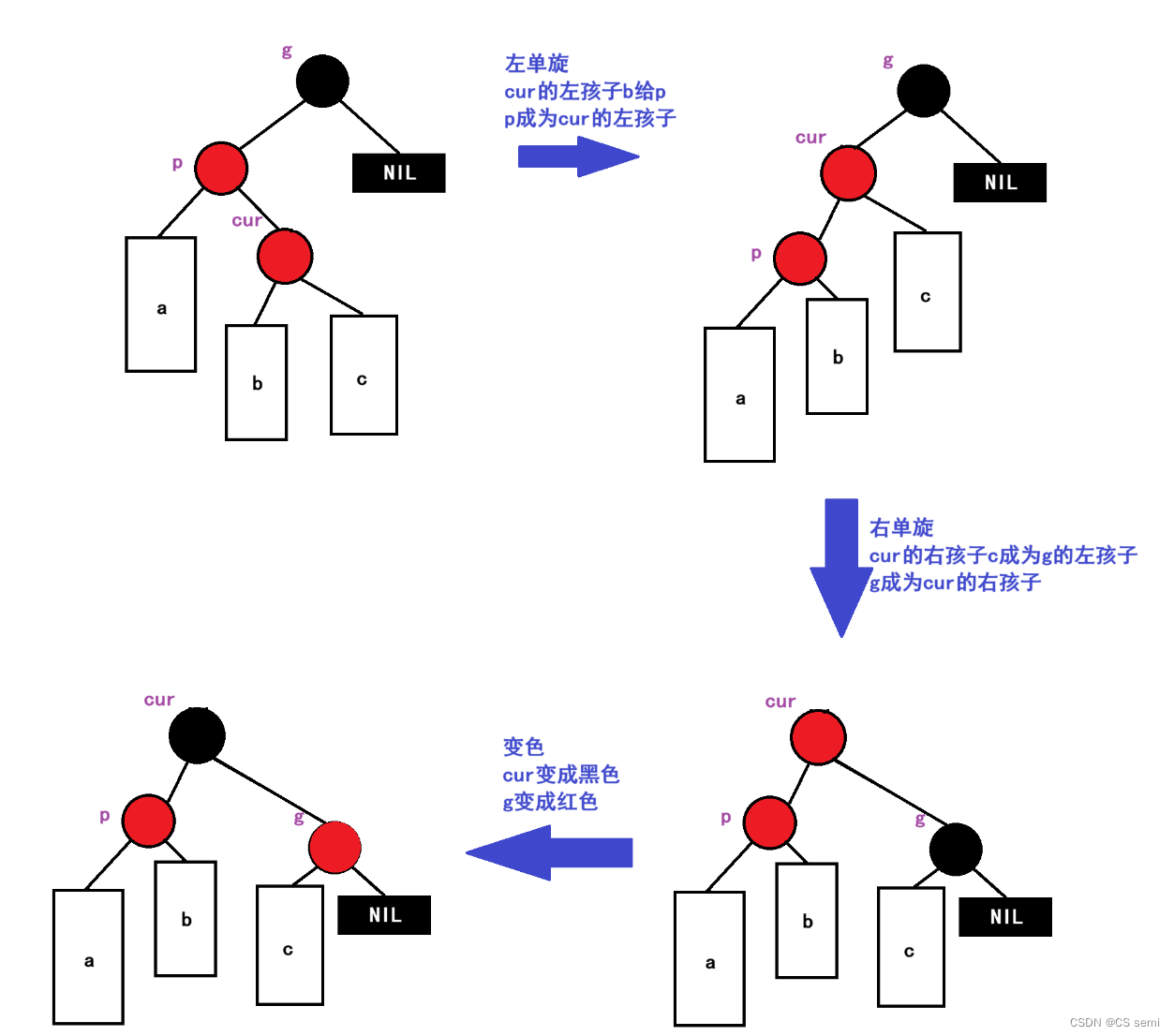
若p是g的右孩子,cur是p的左孩子的时候,是右左双旋,再进行改变颜色。
代码操作
我们在进行代码书写之前,我们需要了解一下pair中的尖括号有一个很奇妙的作用,也就是前面存储指针,后面存储bool值,显示是不是插入成功。我们可以简单了解一下:pair<Node*, true>和<Node*, false>,前面一个代表插入的指针,后面一个变量表明是否插入成功。
// 插入pair<Node*, bool> Insert(const pair<K, V>& kv){// 一棵空树if (_root == nullptr){// 创建新结点 + 颜色初始化为黑色_root = new Node(kv);_root->_col = BLACK; // 根节点得是黑的return make_pair(_root, true);}// 先找到 -- 利用二叉搜索树的方法进行查找Node* cur = _root;Node* parent = nullptr;// 左小右大while (cur){// 当前结点值大于待插入结点值,往左子树走if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}// 当前结点值小于待插入结点值,往右子树走else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}// 待插入结点的值和当前结点的值相等,插入失败else{return make_pair(cur, false);}}// 将当前结点的值插入进去cur = new Node(kv); // new一个新的结点cur->_col = RED;Node* newnode = cur; // 记录新插入的结点// 新插入的节点值小于父节点的节点值,插入到parent的左边if (kv.first < parent->_kv.first){parent->_left = cur;cur->_parent = parent;}// 新插入的节点值小于父节点的节点值,插入到parent的左边else{parent->_right = cur;cur->_parent = parent;}// 新插入结点的父节点是红色的,需要做出调整while (parent && parent->_col == RED){Node* grandfather = parent->_parent; // parent是红色,则其父结点一定存在// 以grandparent左右孩子为分界线,分成if和elseif (parent == grandfather->_left) // 左孩子{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)// 情况一:uncle存在且为红色{// 颜色调整grandfather->_col = RED;uncle->_col = parent->_col = BLACK;// 继续往上处理cur = grandfather;parent = cur->_parent;}else// 情况二:uncle存在且为黑色 / 情况三:uncle不存在{// 用左右孩子分为两半,一半是if用来表示在左孩子,一半是else用来表示在右孩子if (cur == parent->_left){// g// p// c// 右单旋RoateR(grandfather);// 颜色调整parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// c// 左右双旋RoateLR(grandfather);// 颜色调整cur->_col = BLACK;grandfather->_col = RED;}break;}}else // 右孩子{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)// 情况一:uncle存在且为红色{// 颜色调整grandfather->_col = RED;uncle->_col = parent->_col = BLACK;// 继续往上处理cur = grandfather;parent = cur->_parent;}else// 情况二:uncle存在且为黑色 / 情况三:uncle不存在{// 用左右孩子分为两半,一半是if用来表示在左孩子,一半是else用来表示在右孩子if (cur == parent->_right){// g// p// c// 左单旋RoateL(grandfather);// 颜色调整parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// c// 右左双旋RoateRL(grandfather);// 颜色调整cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}// 左单旋void RoateL(Node* parent){// 三叉链Node* subr = parent->_right;Node* subrl = subr->_left;Node* ppnode = parent->_parent;// subrl与parent的关系parent->_right = subrl;if (subrl)subrl->_parent = parent;// subl和parent的关系subr->_left = parent;parent->_parent = subr;// ppnode和subr的关系if (ppnode == nullptr){_root = subr;subr->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subr;}else{ppnode->_right = subr;}subr->_parent = ppnode;}}// 右单旋void RoateR(Node* parent){// 三叉链Node* subl = parent->_left;Node* sublr = subl->_right;Node* ppnode = parent->_parent;//sublr和parent之间的关系parent->_left = sublr;if (sublr)sublr->_parent = parent;//subl和parent的关系subl->_right = parent;parent->_parent = subl;//ppnode 和 subl的关系if (ppnode == nullptr){_root = subl;subl->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subl;}else{ppnode->_right = subl;}subl->_parent = ppnode;}}// 左右双旋void RoateLR(Node* parent){RoateL(parent->_left);RoateR(parent);}// 右左双旋void RoateRL(Node* parent){RoateR(parent->_right);RoateL(parent);}
五、验证是否是红黑树
先验证一下是否是平衡二叉树。
// 中序遍历void InOrder(){return _InOrder(_root);}void _InOrder(Node* root){if (root == nullptr)return;// 中序_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}
// 验证是否平衡// 先检查检查颜色bool CheckColour(Node* root, int blacknum, int blenchnum) // 基准值{if (root == nullptr){// 每个路径黑色不相等if (blacknum != blenchnum){return false;}return true;}// 黑色增加if (root->_col == BLACK){++blacknum;}// 连续红色结点情况if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续的红色结点" << endl;return false;}// 递归return CheckColour(root->_left, blacknum, blenchnum)&& CheckColour(root->_right, blacknum, blenchnum);}// 再检查是否平衡bool IsRBTree(){return _IsRBTree(_root);}bool _IsRBTree(Node* root){if (root == nullptr){return true;}if (root->_col == RED){return false;}// 找最左路径作为黑色结点数目的参考值int blenchnum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++blenchnum;cur = cur->_left;}return CheckColour(root, 0, blenchnum);}
六、红黑树的高度
其实很简单,红黑树的高度算的是左右子树中最高的那个树的层数的高度,所以我们仅仅需要计算一下左右子树中最高的那棵子树即可。
// 计算树的高度int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr){return 0;}int leftcount = _Height(root->_left);int rightcount = _Height(root->_right);return leftcount > rightcount ? leftcount + 1 : rightcount + 1;}
七、红黑树的查找
与搜索二叉树的查找方式是一模一样的:
1、要找的值比当前结点小,往左子树走
2、要找的值比当前结点大,往右子树走
3、要找的值等于当前结点,找到了
4、找到空都没找到,则返回空
// 红黑树的查找Node* Find(const pair<K, V>& kv){Node* cur = _root;while (cur){// 当前结点的值大于寻找的结点的值if (cur->_kv.first > kv.first){cur = cur->_left;}else if(cur->_kv.first < kv.first){cur = cur->_right;}else{// 找到了return cur;}}return nullptr;}
八、红黑树的删除
第一步:先找待删除的结点
与搜索二叉树大致相同,如果我们找到待删除的结点的左右子树不为空,则需使用替换法进行删除,所以我们最终需要删除的都是左右子树至少有一个为空的结点。
第二步:调整红黑树
同样跟AVL树一样,先需要判断是否对红黑树的颜色有影响,如果破坏了红黑树的四条性质那就需要调整红黑树。
如果本次删除结点为红色结点的话,那么本次删除操作不会破坏红黑树的性质,因此我们不需要对红黑树进行调整。然而如果本次删除的结点为黑色结点的话,那么本次删除操作必然会破坏红黑树的性质,因为黑色结点的减少必然会破坏性质四,所以就需要对红黑树做出调整。
(一)情况一
待删除的结点只有一个孩子,左孩子/右孩子,即待删除的结点是只有一个孩子为空的情况。
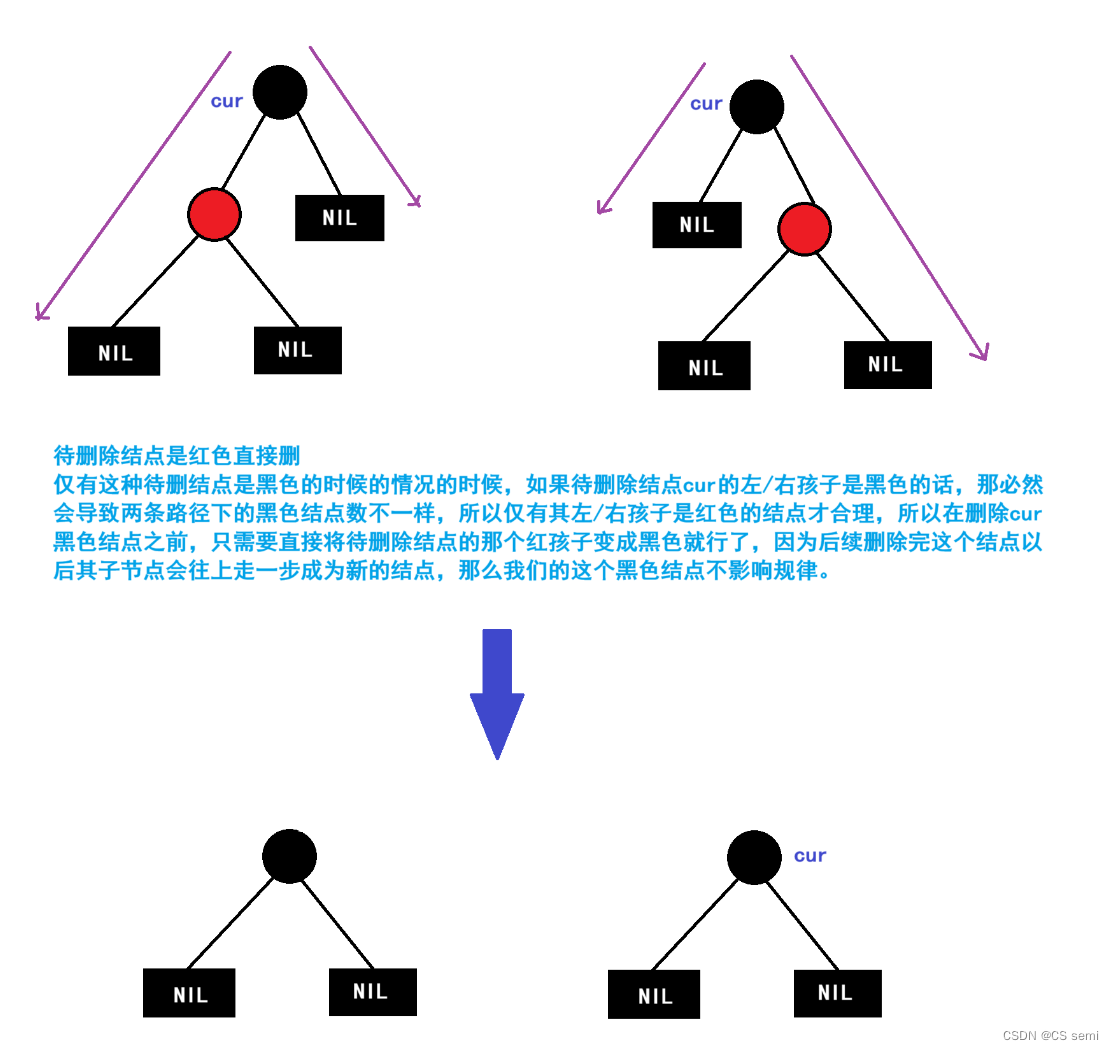
(二)情况二
待删除结点的左右孩子的结点都是空的。
我们以待删除结点是其父结点的左孩子为例,分为以下四种情况:
1、brother为红色

当待删结点的brother为红色的情况下,先以parent为旋转点进行左单旋,将brother当老大,再进行颜色的调整,brother变成黑色,parent变成红色,我们再对cur做分析,这样就是下面三种情况了。
2、brother为黑色,且其左右孩子都是黑色结点或为空
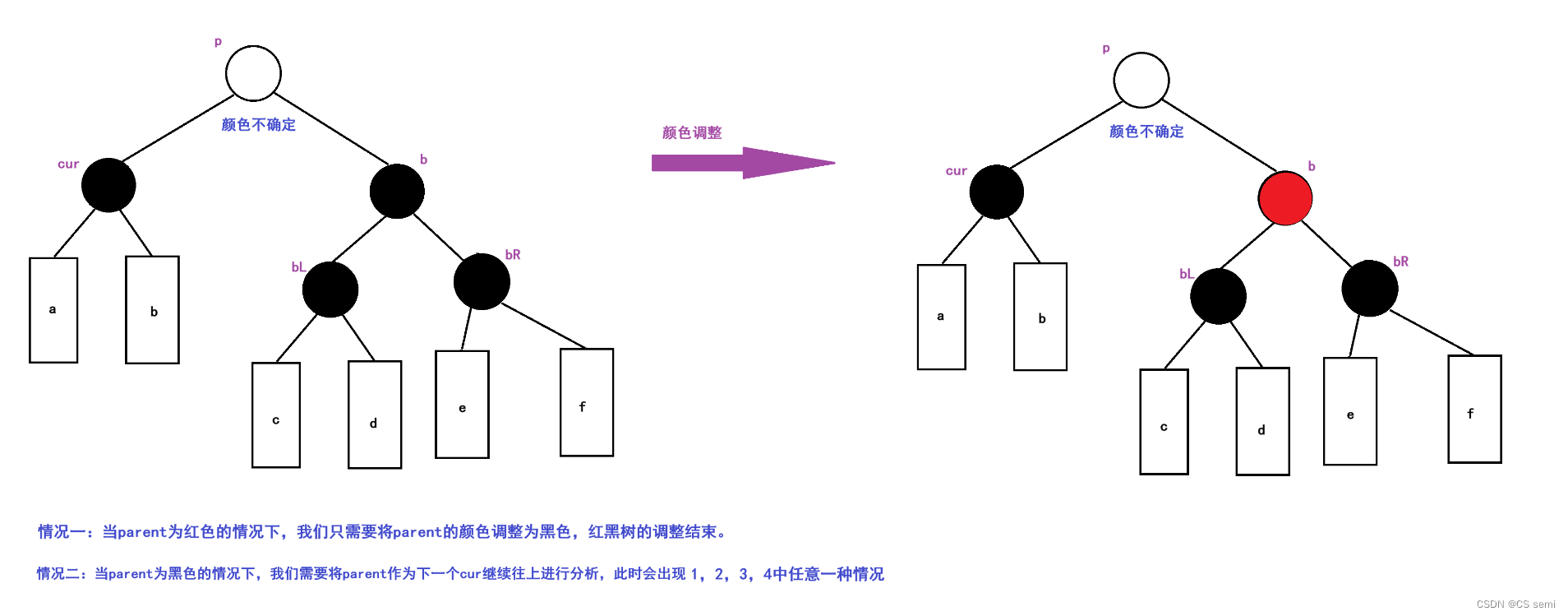
3、brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空
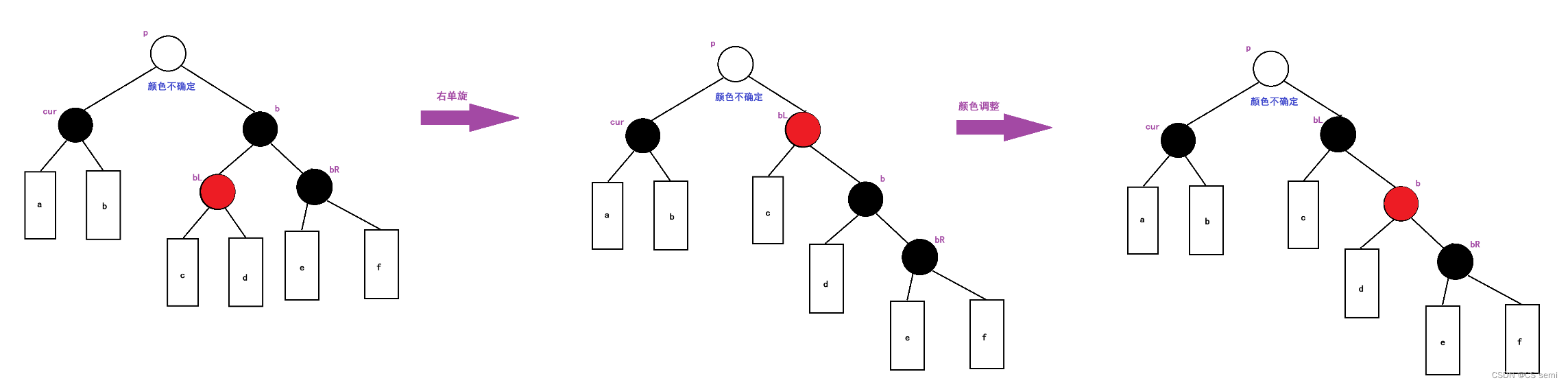
我们先以brother为旋转点进行右单旋,再将brother颜色变红,brotherleft颜色变黑,再需要根据情况变成情况四的情况。
4、brother为黑色,且其右孩子是红色结点
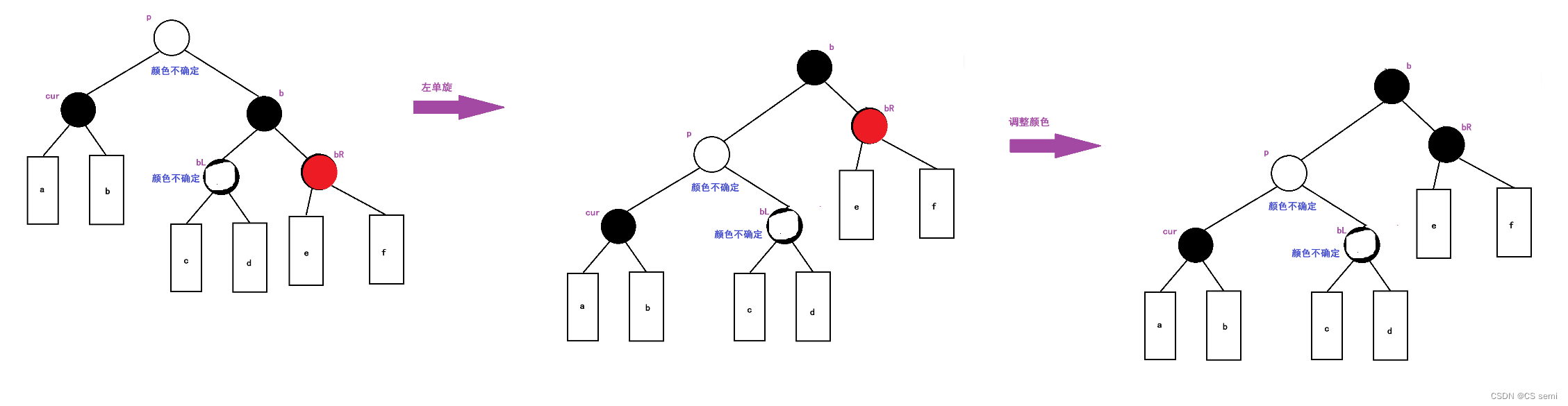
我们进入到第四种情况时候,就结束了调整,以parent为旋转点进行一次左单旋,然后将parent的颜色赋值给brother,再将parent的颜色变为黑色,最后将brotherRight变为黑色。
(三)右边子树
右边子树和左边子树是大同小异的。
(四)情况说明
我们总共有四种情况,最重要的是我们需要走到第四种情况,这样红黑树的调整才是好了,所以,我们有下面的关系:
1->2,3,4
2->1,2,3,4
3->4
4->结束
我们知道了关系,所以,4是一定能退出的,3能够转化到4然后退出的,1能够转化为2,3,4也是有办法退出的,而只有2这种情况最纠结了,因为刚进入2这种情况parent的颜色是个迷,不管是黑色还是红色都是没有问题的!
(五)删除操作
根据搜索二叉树的删除规则,连接这个结点的左/右孩子即可。
代码
// 删除bool Erase(const K& key){// 用于遍历二叉树找结点Node* parent = nullptr;Node* cur = _root;// 用于标记实际的删除结点及其父结点Node* delparentpos = nullptr;Node* delpos = nullptr;// 先找到while (cur){// 所给key值小于当前节点的值 -- 往左树走if (key < cur->_kv.first){parent = cur;cur = cur->_left;}// 所给key值大于当前结点的值 -- 往右树走else if (key > cur->_kv.first){parent = cur;cur = cur->_right;}// 找到了else{// 左子树为空if (cur->_left == nullptr){// 待删除结点是根节点if (cur == _root){// 让根节点的右子树作为新的结点_root = _root->_right;if (_root)_root->_parent = nullptr;delete cur; // 删除原节点return true;}else // 不是根节点{delparentpos = parent; // 标记当前待删除结点的父节点delpos = cur; // 标记当前待删除的结点}break; // 删除结点有祖先的结点,需要更新平衡因子}// 右子树为空else if (cur->_right == nullptr){// 待删除结点是根节点if (cur == _root){// 让根节点的左子树作为新的结点_root = _root->_left;if (_root)_root->_parent = nullptr;delete cur; // 删除原节点return true;}else // 不是根节点{delparentpos = parent; // 标记当前待删除结点的父节点delpos = cur; // 标记当前待删除的结点}break; // 删除结点有祖先的结点,需要更新平衡因子}// 左右子树都不为空else{// 替换法// 寻找待删除结点的右子树中的最小值Node* minparent = cur;Node* minright = cur->_right;while (minright->_left){minparent = minright; // 记录一下父节点minright = minright->_left; // 往左子树走}cur->_kv.first = minright->_kv.first;// 将待删除结点first替换为右子树的最小值cur->_kv.second = minparent->_kv.second;// 将待删除结点second替换为右子树的最小值// 记录一下要删除的父节点delparentpos = minparent;// 记录一下实际要删除的结点delpos = minright;break; // 祖先结点的平衡因子需要改变}}}// 没有被修改过,说明没找到当前要删除的结点if (delparentpos == nullptr)return false;// 记录当前要删除结点和当前要删除结点的父节点Node* del = delpos;Node* delP = delparentpos;// 调整红黑树if (delpos->_col == BLACK){if (delpos->_left && delpos->_left->_col == RED) //待删除结点有一个红色的左孩子{// delpos// _leftdelpos->_left->_col = BLACK; //将这个红色的左孩子变黑}else if (delpos->_right && delpos->_right->_col == RED) //待删除结点有一个红色的右孩子{// delpos// _rightdelpos->_right->_col = BLACK; //将这个红色的右孩子变黑}else // 待删除结点的左右均为空{while (delpos != _root){// 待删除的结点是其父节点的左孩子if (delpos == delparentpos->_left){// delparentpos// delpos brotherNode* brother = delparentpos->_right; // 兄弟结点是其父结点的右孩子// 情况1:brother为红色if (brother->_col){// 先左旋再调颜色RoateL(delparentpos);delparentpos->_col = RED;brother->_col = BLACK;// 继续向上调整brother = delparentpos->_right;}// 情况2:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;// 分情况if (delparentpos->_col == RED){delparentpos->_col = BLACK;break;}// 向上调整delpos = delparentpos;delparentpos = delpos->_parent;}else{// 情况3:brother为黑色,且其右孩子是红色结点// 左旋RoateL(delparentpos);brother->_col = delparentpos->_col;delparentpos->_col = BLACK;brother->_right->_col = BLACK;break;// 情况4:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空if ((brother->_right == nullptr) || (brother->_right->_col == BLACK)){brother->_left->_col = BLACK;brother->_col = RED;RoateR(brother);brother = delparentpos->_right; }}}// 待删除的结点是其父节点的右孩子else{Node* brother = delparentpos->_right; // 兄弟结点是其父结点的右孩子// 情况1:brother为红色if (brother->_col == RED){RoateR(delparentpos);delparentpos->_col = RED;brother->_col = BLACK;// 继续向上调整brother = delparentpos->_left;}// 情况2:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delparentpos->_col == RED){delparentpos->_col = BLACK;break;}delpos = delparentpos;delparentpos = delpos->_parent;}else{// 情况3:brother为黑色,且其右孩子是红色结点RoateR(delparentpos);brother->_col = delparentpos->_col;delparentpos->_col = BLACK;brother->_left->_col = BLACK;break;// 情况4:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空if ((brother->_left == nullptr) || (brother->_left->_col == BLACK)){brother->_right->_col = BLACK;brother->_col = RED;RoateL(brother);brother = delparentpos->_left;}}}}}}// 进行删除// 删除的结点的左子树是空树if (del->_left == nullptr){if (del == delP->_left) //删除结点是其父结点的左孩子{delP->_left = del->_right;if (del->_right)del->_right->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_right;if (del->_right)del->_right->_parent = delP;}}else // 删除的结点的右子树是空树// del->_right == nullptr {if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_left;if (del->_left)del->_left->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_left;if (del->_left)del->_left->_parent = delP;}}delete del;return true;}
九、红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
相关文章:

【高阶数据结构】红黑树(C++实现)
⭐博客主页:️CS semi主页 ⭐欢迎关注:点赞收藏留言 ⭐系列专栏:C进阶 ⭐代码仓库:C进阶 家人们更新不易,你们的点赞和关注对我而言十分重要,友友们麻烦多多点赞+关注,你们的支持是我…...

算力百川汇蓝海,商海荡漾绘宏图
算力百川汇蓝海 01 新兴技术呼唤算力 崭新时代逐浪前,科技浪潮涌向天。 人工智能、数字孪生、元宇宙等新兴技术的迅速发展,引爆全球算力需求的规模式增长。尤其,以ChatGPT为代表的人工智能技术发展,引发了全球算力需求的进一步增长…...
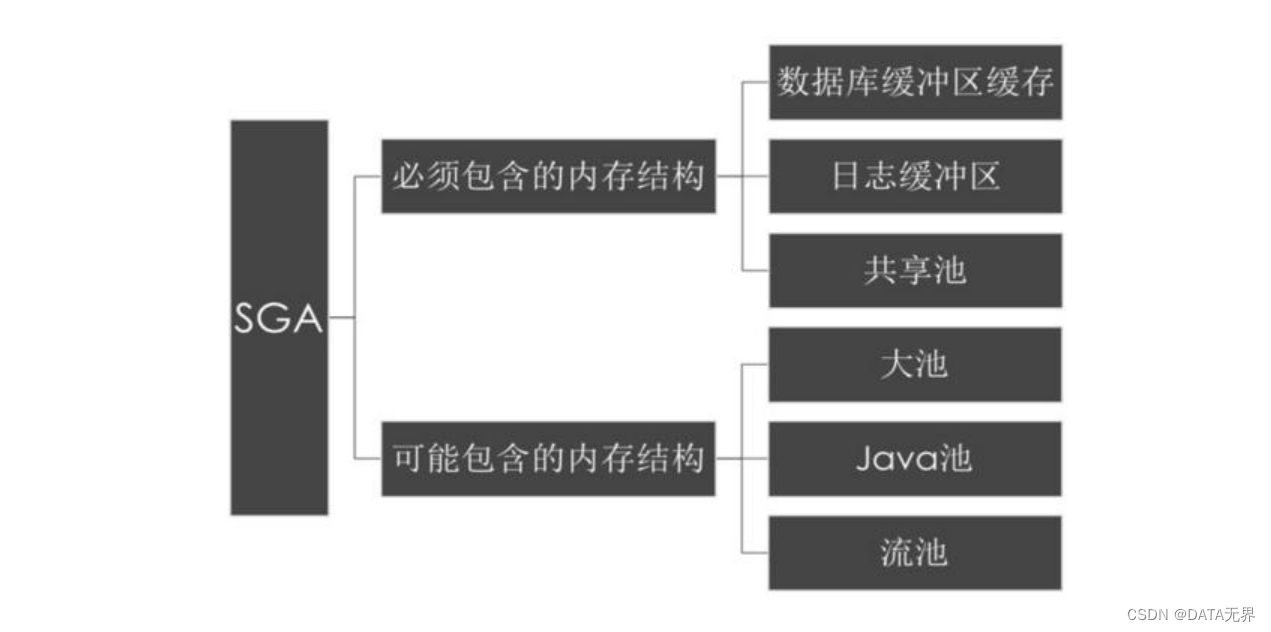
ORACLE 内存结构之系统全局区(SGA)
每个 Oracle 数据库实例都会在内存中分配一个很大的内存结构, 称为系统全局区(System Global Area), 这是一个大型的共享内存结构,每个Oracle进程都会访问它。 在Linux/Unix操作系统上,SGA是一个物理实体,使用操作系统命令能“看到它”。 它被操作系…...

主要文档分享网站一览
136****0621的全部文档-第1页-原创力文档 目前能提供上传文档并付费的网站: 1、得利文库 www.deliwenku.com 先说我自已的吧!见笑了 2、百度文库 wenku.baidu.com 这个算头部了、有流量倾斜、但资源多、用户现在上传的大部份为重复的,…...

CPU访问一个虚拟地址的整体流程
一、虚拟地址转换成物理地址 涉及到的部件: MMU:虚拟地址—MMU—>物理地址。MMU会控制整个流程(查快表、查慢表等等)TLB快表:组号(若为组相联TLB)、TLB标记、有效位、页框号页表(…...
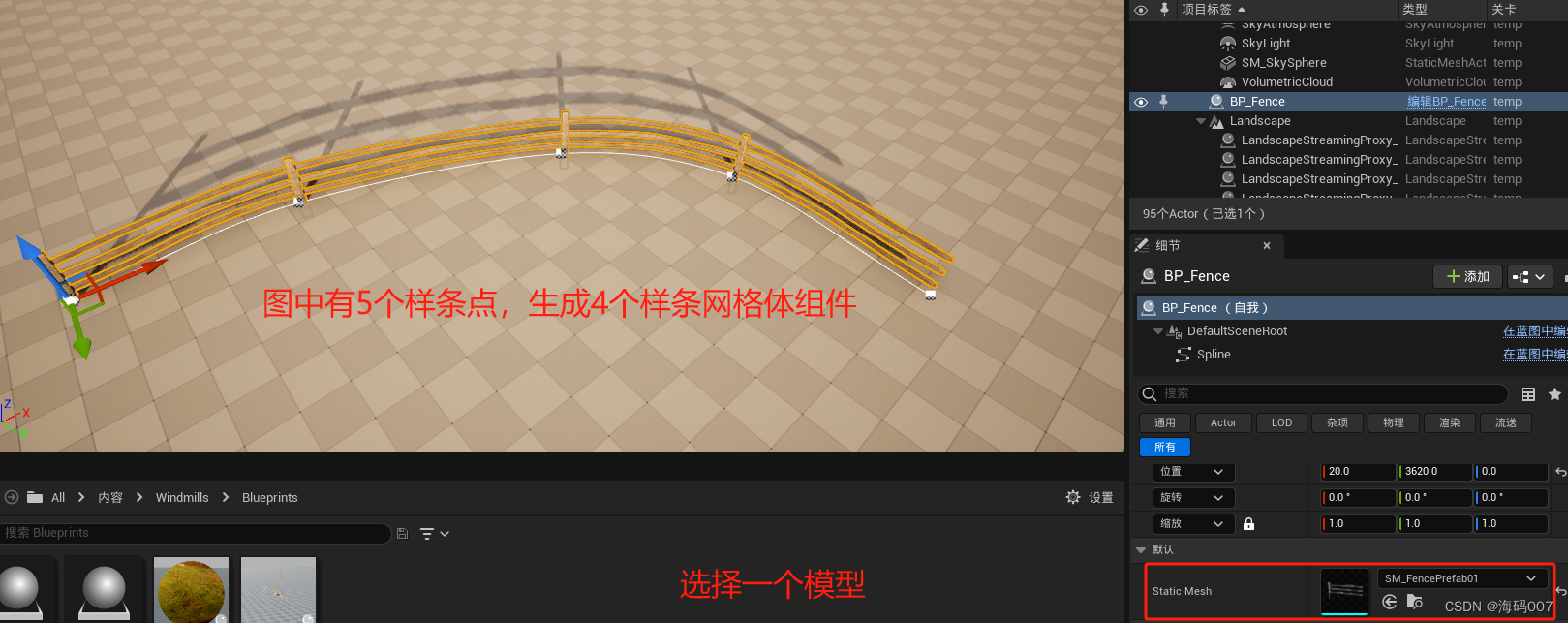
UE5 虚幻引擎 如何使用构造脚本(Construction Script)? 构造脚本的奥秘!
目录 1 构造脚本(Construction Script)1.1 介绍1.2 案例1:利用样条组件程序化生成树木1.2 案例2:利用样条组件和样条网格体组件程序化生成道路 1 构造脚本(Construction Script) 1.1 介绍 问题:…...
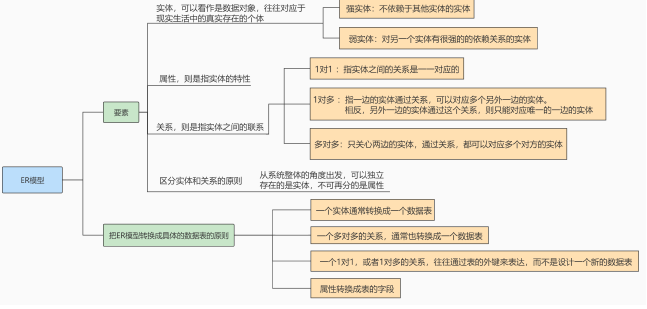
Mysql高级——数据库设计规范(2)
8. ER模型 ER 模型中有三个要素,分别是实体、属性和关系。 实体,可以看做是数据对象,往往对应于现实生活中的真实存在的个体。在 ER 模型中,用矩形来表示。实体分为两类,分别是强实体和弱实体。强实体是指不依赖于其…...
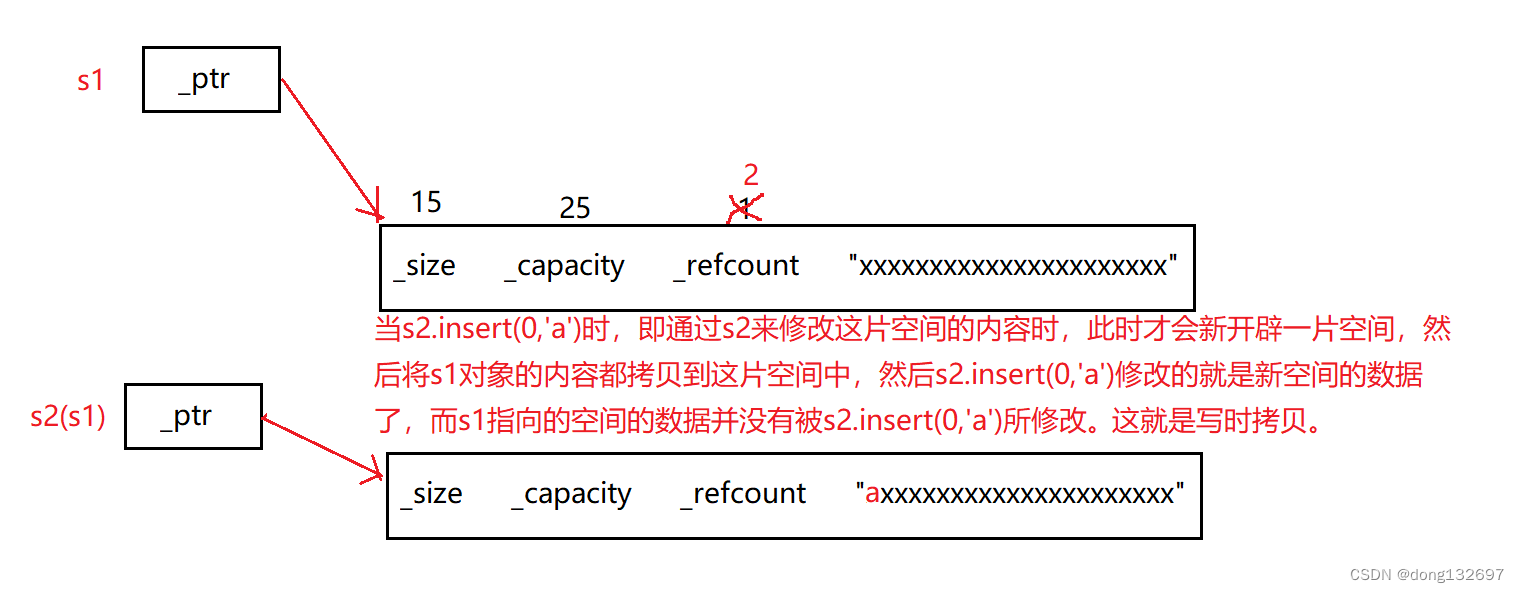
c++-string
文章目录 前言一、STL库介绍二、标准库中的string类1、string类介绍2、string类使用3.1 string类的构造函数3.2 string类对象的容量操作3.3 string类对象的遍历操作3.4 string类对象的访问操作3.5 string类对象的修改操作3.6 string类对象的字符串操作 三、模拟实现string类四、…...

KNN-K近邻算法(K-Nearest Neighbors)
k近邻算法的特点 思想极度简单应用数学知识少(近乎为零)效果好(缺点?)可以解释机器学习算法使用过程中的很多细节问题更完整的刻画机器学习应用的流程 k近邻算法 k近邻算法整体是这样的一个算法,我们已经知道的这些数据点其实是…...

ChatGPT:理解HTTP请求数据格式:JSON、x-www-form-urlencoded和form-data
ChatGPT:理解HTTP请求数据格式:JSON、x-www-form-urlencoded和form-data 使用postman发送一个post请求,在body里面加上了form-data数据,namexxx,age23,为什么输出request.body()得到的是这样的结果 -------…...

字符集、IO流(一)
字符集、IO流(一) 各位同学,前面我们已经学习了File类,通过File类的对象可以对文件进行操作,但是不能操作文件中的内容。要想操作文件中的内容,我们还得学习IO流。但是在正式学习IO流之前,我们还需要学习一个前置知识叫做字符集,只有我们把字符集搞明白了,再学习IO流…...
)
相乘(蓝桥杯)
相乘 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小蓝发现,他将 1 至 1000000007 之间的不同的数与 2021 相乘后再求除以 1000000007 的余数,会得到不同的数。 小蓝想知道,能不能在 1 …...
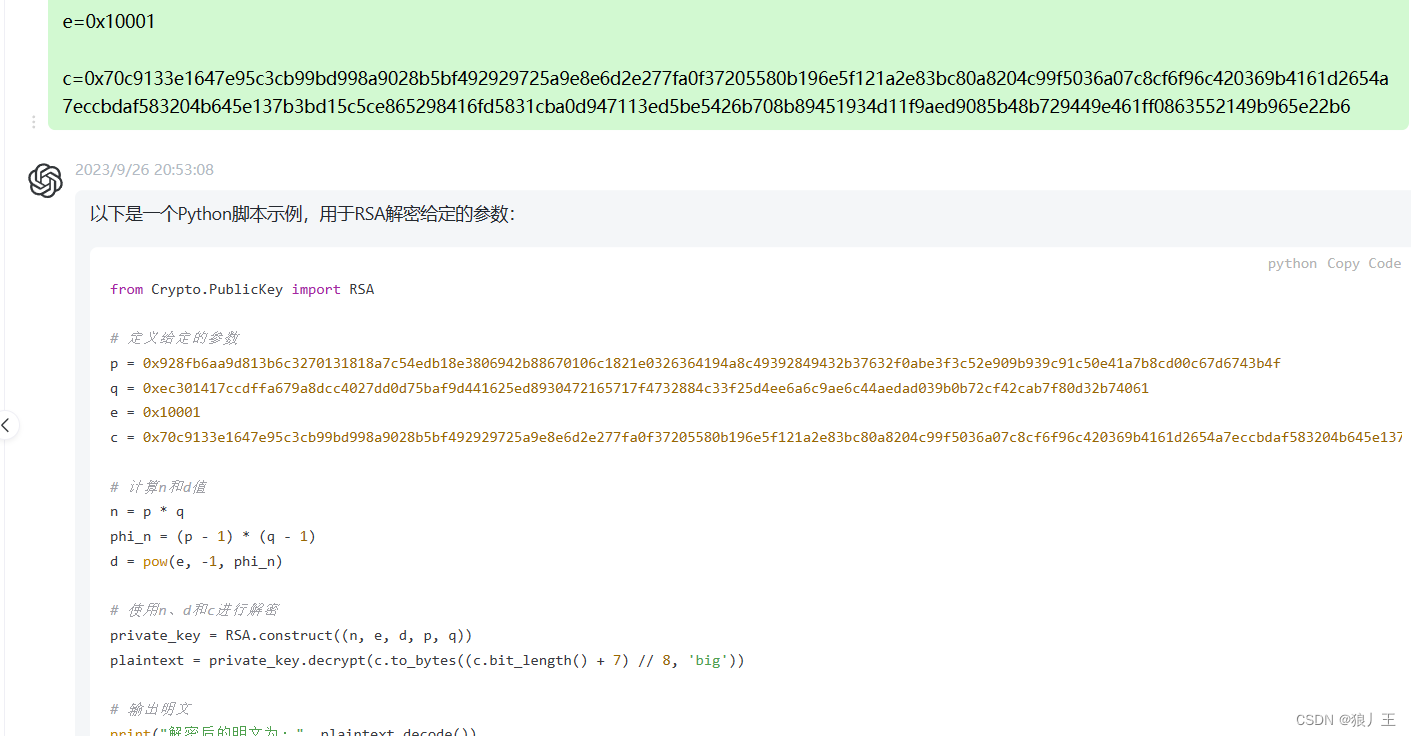
[AFCTF 2018]你能看出这是什么加密么
最开始是我对rsa的小小的理解 rsa也就是非对称加密算法,拥有公开的加密密钥和解密密钥,这也是我们写脚本的基础 选取素数p和q,计算乘积npq,以及(n)(p-1)(q-1)。(欧拉函数) 选择一个e值作为密钥…...
基于springboot+vue的重庆旅游网(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

pymysql执行delete删除操作
视频版教程 Python操作Mysql数据库之pymysql模块技术 执行delete操作,雷同前面的update操作 from pymysql import Connectioncon Nonetry:# 创建数据库连接con Connection(host"localhost", # 主机名port3306, # 端口user"root", # 账户…...

25862-2010 制冷与空调用同轴套管式换热器
声明 本文是学习GB-T 25862-2010 制冷与空调用同轴套管式换热器. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了制冷与空调用同轴套管式换热器(以下简称"换热器")的术语和定义、基本参数、要 求、试验、检验规则、标…...

JetBrains 产品安装插件(plugins)的两种方式
安装分为在线、离线两种方式: 在线方式: File > Settings > Plugins 搜索插件 Install 即可 离线方式: 官网:https://plugins.jetbrains.com/ 搜索到插件后,点击 "Get",选择自己安装的…...
SOLIDWORKS二次开发
SOLIDWORKS是一套三维设计软件, 采用特征建模、变量化驱动可方便地实现三维建模、装配和生成工程图。SOLIDWORKS软件本身所具有的交互方式,可以使用户对已生成模型的尺寸、几何轮廓和相互约束关系随时进行修改, 而不需要编程。SOLIDWORKS软件本身的方程式可以实现简…...

Linux下压缩和解压缩
在Linux下,您可以使用多种命令来进行文件和目录的压缩和解压缩操作。以下是一些常见的压缩和解压缩命令: tar:tar命令可用于创建和提取tar压缩文件。例如,要创建一个名为archive.tar的.tar文件,可以使用以下命令&#…...

爬虫入门基础-HTTP协议过程
在进行网络爬虫开发之前,了解HTTP协议的基本过程是非常重要的。HTTP协议是Web通信的基础,也是爬取网页数据的核心。本文将为您详细介绍HTTP协议的过程,帮助您理解爬虫背后的网络通信机制。让我们一起来探索吧! 一、什么是HTTP协议…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
