debug过程中,矩阵左乘右乘相关概念梳理
1. 变换点或者变换向量
1.1左乘
矩阵左乘通常是指对”目标点“进行左乘,即:
A ′ = R ∗ A A'=R*A A′=R∗A
其中,A为原始3维点,表示一个3*1的列向量,R为33的旋转矩阵,A‘为变换后的点
B ′ = T ∗ B B'=T*B B′=T∗B
其中,B为原始点3维点,表示一个4*1的齐次化列向量,T为44的旋转矩阵R|t,B‘为变换后的点
以此类推,
如果是点云 c l o u d s r c = { X s r c ∣ X s r c = A 1 , A 2 … … A n } cloud_{src}=\{X_{src}|X_{src}=A_1,A_2……A_n\} cloudsrc={Xsrc∣Xsrc=A1,A2……An},A表示一个3*1的列向量
此时 X s r c X_{src} Xsrc为一个3*n的矩阵,那么变换可以表示为
X A ′ = R ∗ X A X_A'=R*X_A XA′=R∗XA
X B ′ = T ∗ X B X_B'=T*X_B XB′=T∗XB
1.1.1矩阵与旋转角
上面为3维点的变换,为了方便画图解释下面以2维点进行描述:
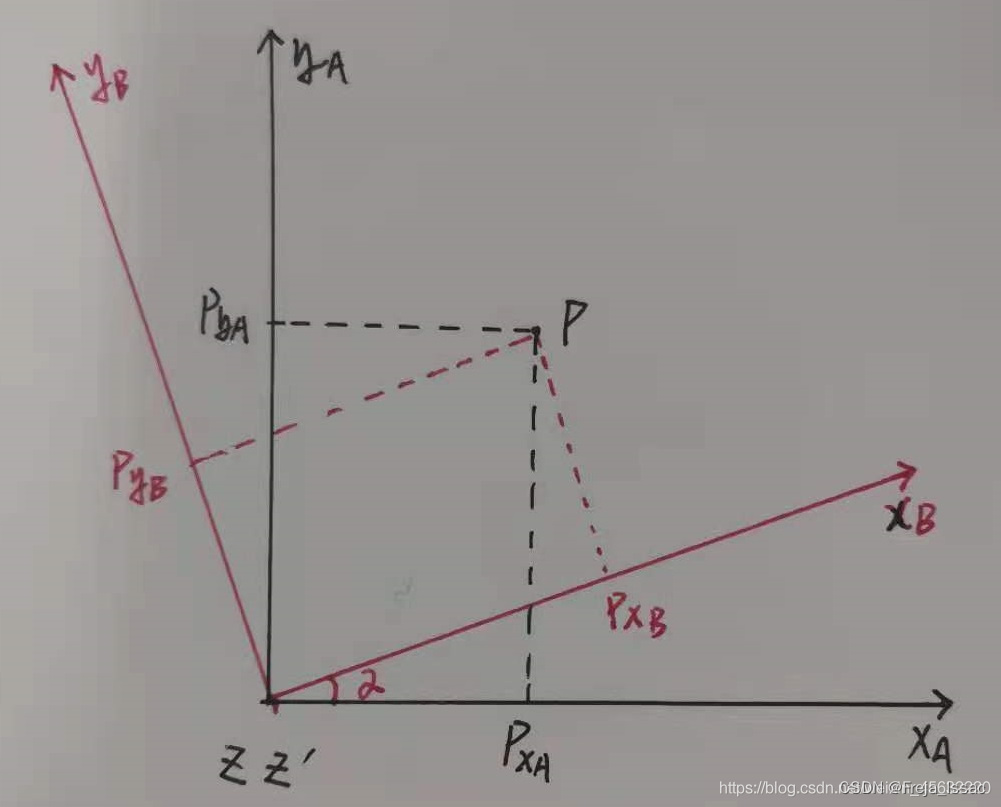
P A = R ∗ P B P_A = R*P_B PA=R∗PB
将矩阵乘法展开可以写为:
[ P x A P y A P z A ] = [ c o s ( α ) − s i n ( α ) 0 s i n ( α ) c o s ( α ) 0 0 0 1 ] ∗ [ P x B P y B P z B ] \begin{bmatrix} P_{xA}\\P_{yA}\\P_{zA} \end{bmatrix} = \begin{bmatrix} cos(\alpha) & -sin(\alpha) & 0 \\ sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{bmatrix}*\begin{bmatrix} P_{xB}\\P_{yB}\\P_{zB} \end{bmatrix} PxAPyAPzA = cos(α)sin(α)0−sin(α)cos(α)0001 ∗ PxBPyBPzB
上面图片表示的是一个矩阵的左乘,其中旋转矩阵R表达的是B点绕z轴逆时针旋转 α \alpha α度,得到A点。
如果是旋转一个坐标系的话,那么上面的矩阵表示的就是坐标B系绕Z轴顺时针旋转 α \alpha α度,得到A坐标系。
PS:此处顺逆时针都是Z轴朝上的,如果Z轴朝下,表达方式会有所不同。
这两个的表达是一个意思,矩阵表达也是一样的。(原因在于:虽然都是左乘,顺逆时针虽然相反,但是旋转矩阵R的选择是等价的,因此,从方程表达上是一样的。)
Z轴逆时针旋转点的R矩阵<==>Z轴顺时针旋转坐标系的R矩阵
[ c o s ( α ) − s i n ( α ) 0 s i n ( α ) c o s ( α ) 0 0 0 1 ] \begin{bmatrix} cos(\alpha) & -sin(\alpha) & 0 \\ sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{bmatrix} cos(α)sin(α)0−sin(α)cos(α)0001
Z轴顺时针旋转点的R矩阵<==>Z轴逆时针旋转坐标系的R矩阵
[ c o s ( α ) s i n ( α ) 0 − s i n ( α ) c o s ( α ) 0 0 0 1 ] \begin{bmatrix} cos(\alpha) & sin(\alpha) & 0 \\ -sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{bmatrix} cos(α)−sin(α)0sin(α)cos(α)0001
1.2右乘
没有具体例子:
1.3 左乘右乘同时存在的场景
针对transform增量(例如A坐标系下的R|t),变换坐标系的场景
求:点云 X A w o r l d X_A^{world} XAworld与点云 X B w o r l d X_B^{world} XBworld进行icp匹配,得到A点云到B点云的相对位姿 T A − > B w o r l d T_{A->B}^{world} TA−>Bworld
已知,
lidar是一个在移动车辆上的sensor,输出A时刻,相对lidar坐标系的点云为 X A l i d a r X_A^{lidar} XAlidar;输出B时刻,相对lidar坐标系的点云为 X B l i d a r X_B^{lidar} XBlidar
imu是一个在移动车辆上的sensor,输出结果为mct坐标系下的结果,把mct坐标系下第一帧的时刻定义为固定坐标系:世界坐标系
P P i m u A w o r l d PP_{imu_A}^{world} PPimuAworldimu在A时刻的世界坐标系下,位姿矩阵PPa
P P i m u B w o r l d PP_{imu_B}^{world} PPimuBworldimu在B时刻的世界坐标系下,位姿矩阵PPb
imu到lidar的外参可以表述为 T i m u l i d a r = T m c t l i d a r T_{imu}^{lidar}=T_{mct}^{lidar} Timulidar=Tmctlidar,因为imu输出结果是在mct系下,所以外参可以看作是mct坐标系到lidar坐标系的变换
求解:
lidar的A时刻在世界坐标系(mct系)下的位姿矩阵为: P P l i d a r A w o r l d = P P i m u A w o r l d ∗ T i m u l i d a r = P P i m u A w o r l d ∗ T m c t l i d a r PP_{lidar_A}^{world}=PP_{imu_A}^{world}*T_{imu}^{lidar}=PP_{imu_A}^{world}*T_{mct}^{lidar} PPlidarAworld=PPimuAworld∗Timulidar=PPimuAworld∗Tmctlidar
lidar的B时刻在世界坐标系(mct系)下的位姿矩阵为: P P l i d a r B w o r l d = P P i m u B w o r l d ∗ T i m u l i d a r = P P i m u B w o r l d ∗ T m c t l i d a r PP_{lidar_B}^{world}=PP_{imu_B}^{world}*T_{imu}^{lidar}=PP_{imu_B}^{world}*T_{mct}^{lidar} PPlidarBworld=PPimuBworld∗Timulidar=PPimuBworld∗Tmctlidar
A时刻,相对世界坐标系(mct系)的点云为 X A w o r l d = P P l i d a r A w o r l d ∗ X A l i d a r X_A^{world} = PP_{lidar_A}^{world}*X_A^{lidar} XAworld=PPlidarAworld∗XAlidar,
可展开为: X A w o r l d = P P i m u A w o r l d ∗ T m c t l i d a r ∗ X A l i d a r X_A^{world} = PP_{imu_A}^{world}*T_{mct}^{lidar}*X_A^{lidar} XAworld=PPimuAworld∗Tmctlidar∗XAlidar
B时刻,相对世界坐标系(mct系)的点云为 X B w o r l d = P P l i d a r B w o r l d ∗ X B l i d a r X_B^{world} = PP_{lidar_B}^{world}*X_B^{lidar} XBworld=PPlidarBworld∗XBlidar
可展开为: X B w o r l d = P P i m u B w o r l d ∗ T m c t l i d a r ∗ X B l i d a r X_B^{world} = PP_{imu_B}^{world}*T_{mct}^{lidar}*X_B^{lidar} XBworld=PPimuBworld∗Tmctlidar∗XBlidar
经过icp匹配 X A w o r l d X_A^{world} XAworld和 X B w o r l d X_B^{world} XBworld可以得到 T A − > B w o r l d T_{A->B}^{world} TA−>Bworld
但是因为imu和lidar时间戳不同步,因此对应时刻imu的位姿矩阵不可信,因此只能得到mct系下AB时刻的点云 X A m c t X_A^{mct} XAmct和 X B m c t X_B^{mct} XBmct
经过icp匹配 X A l i d a r X_A^{lidar} XAlidar和 X B l i d a r X_B^{lidar} XBlidar可以得到变换矩阵 T A − > B l i d a r T_{A->B}^{lidar} TA−>Blidar
经过icp匹配 X A m c t X_A^{mct} XAmct和 X B m c t X_B^{mct} XBmct可以得到变换矩阵 T A − > B m c t T_{A->B}^{mct} TA−>Bmct
其中,
X A m c t = T m c t l i d a r ∗ X A l i d a r X_A^{mct}=T_{mct}^{lidar}*X_A^{lidar} XAmct=Tmctlidar∗XAlidar,
X B m c t = T m c t l i d a r ∗ X B l i d a r X_B^{mct}=T_{mct}^{lidar}*X_B^{lidar} XBmct=Tmctlidar∗XBlidar
那么这个 T A − > B l i d a r T_{A->B}^{lidar} TA−>Blidar和 T A − > B m c t T_{A->B}^{mct} TA−>Bmct表示的是在不同坐标系下的同一个位姿变换矩阵(位姿变换增量矩阵)T=R|t,
这二者之间存在一个固定关系
X A l i d a r X_A^{lidar} XAlidar和 X B l i d a r X_B^{lidar} XBlidar内同一个特征点的坐标为 x A l i d a r x_A^{lidar} xAlidar和 x B l i d a r x_B^{lidar} xBlidar
x A m c t = T l i d a r m c t ∗ x A l i d a r x_A^{mct}=T_{lidar}^{mct}*x_A^{lidar} xAmct=Tlidarmct∗xAlidar,
x B m c t = T l i d a r m c t ∗ x B l i d a r x_B^{mct}=T_{lidar}^{mct}*x_B^{lidar} xBmct=Tlidarmct∗xBlidar
x B m c t = T A − > B m c t ∗ x A m c t x_B^{mct} = T_{A->B}^{mct}*x_A^{mct} xBmct=TA−>Bmct∗xAmct
T l i d a r m c t ∗ x B l i d a r = T A − > B m c t ∗ T l i d a r m c t ∗ x A l i d a r T_{lidar}^{mct}*x_B^{lidar} = T_{A->B}^{mct}*T_{lidar}^{mct}*x_A^{lidar} Tlidarmct∗xBlidar=TA−>Bmct∗Tlidarmct∗xAlidar
x B l i d a r = T A − > B l i d a r ∗ x A l i d a r x_B^{lidar} = T_{A->B}^{lidar}*x_A^{lidar} xBlidar=TA−>Blidar∗xAlidar
T l i d a r m c t ∗ T A − > B l i d a r ∗ x A l i d a r = T A − > B m c t ∗ T l i d a r m c t ∗ x A l i d a r T_{lidar}^{mct}*T_{A->B}^{lidar}*x_A^{lidar} = T_{A->B}^{mct}*T_{lidar}^{mct}*x_A^{lidar} Tlidarmct∗TA−>Blidar∗xAlidar=TA−>Bmct∗Tlidarmct∗xAlidar
T l i d a r m c t ∗ T A − > B l i d a r = T A − > B m c t ∗ T l i d a r m c t T_{lidar}^{mct}*T_{A->B}^{lidar} = T_{A->B}^{mct}*T_{lidar}^{mct} Tlidarmct∗TA−>Blidar=TA−>Bmct∗Tlidarmct
T A − > B l i d a r = ( T l i d a r m c t ) − 1 ∗ T A − > B m c t ∗ T l i d a r m c t T_{A->B}^{lidar} = (T_{lidar}^{mct})^{-1}*T_{A->B}^{mct}*T_{lidar}^{mct} TA−>Blidar=(Tlidarmct)−1∗TA−>Bmct∗Tlidarmct
对应代码:np.dot(np.dot(np.linalg.inv(lidar2mct),delta_mat_mct),lidar2mct)
#验证lidar系下的icp匹配结果与mct系下的icp匹配结果相同
# mct系下的icp匹配结果 表达向量
delta_mat_mct = np.array([[0.999725 , -0.023439 , -0.00130324 , -0.127499] ,
[0.0234409 , 0.999724 , 0.00193209 , 0.0205244] ,
[0.00125752 , -0.0019622 , 0.999999 , -0.00368067] ,
[0.0 , 0.0 , 0.0 , 1]])
# lidar系下的icp匹配结果 表达向量
delta_mat_lidar = np.array([[0.999726 , -0.0234405 , 0.00044465 , -0.0937921] ,
[0.0234395 , 0.999723 , 0.00228773 , 0.140559] ,
[-0.000498197 , -0.00227667 , 0.999998 , -0.00616882] ,
[0 , 0 , 0 , 1]])mct2lidar = np.array([[0.70710678, 0.70710678, 0.0, -1.477],[-0.70710678, 0.70710678, 0.0, -0.77],[0.0, 0.0, 1.0, -0.66],[0.0, 0.0, 0.0, 1.0]])lidar2mct = np.linalg.inv(mct2lidar)
print("mct2lidar : ")
print(mct2lidar)
print("lidar2mct : ")
print(lidar2mct)
print("delta_mat_mct:")
print(delta_mat_mct)
print("delta_mat_lidar -> delta_mat_mct:")
print(np.dot(np.dot(np.linalg.inv(mct2lidar),delta_mat_lidar),mct2lidar))
print("delta_mat_lidar")
print(delta_mat_lidar)
print("delta_mat_mct -> delta_mat_lidar")
#对应公式$T_{A->B}^{lidar} = (T_{lidar}^{mct})^{-1}*T_{A->B}^{mct}*T_{lidar}^{mct}$
print(np.dot(np.dot(np.linalg.inv(lidar2mct),delta_mat_mct),lidar2mct))
运行结果如下:
mct2lidar :
[[ 0.70710678 0.70710678 0. -1.477 ][-0.70710678 0.70710678 0. -0.77 ][ 0. 0. 1. -0.66 ][ 0. 0. 0. 1. ]]
lidar2mct :
[[ 0.70710678 -0.70710678 0. 0.4999245 ][ 0.70710678 0.70710678 0. 1.58886894][ 0. 0. 1. 0.66 ][ 0. 0. 0. 1. ]]
delta_mat_mct:
[[ 0.999725 -0.023439 -0.00130324 -0.127499 ][ 0.0234409 0.999724 0.00193209 0.0205244 ][ 0.00125752 -0.0019622 0.999999 -0.00368067][ 0. 0. 0. 1. ]]
delta_mat_lidar -> delta_mat_mct:
[[ 0.999725 -0.0234385 -0.00130325 -0.12747292][ 0.0234415 0.999724 0.00193208 0.02051356][ 0.00125757 -0.00196213 0.999998 -0.00367863][ 0. 0. 0. 1. ]]
delta_mat_lidar
[[ 9.99726e-01 -2.34405e-02 4.44650e-04 -9.37921e-02][ 2.34395e-02 9.99723e-01 2.28773e-03 1.40559e-01][-4.98197e-04 -2.27667e-03 9.99998e-01 -6.16882e-03][ 0.00000e+00 0.00000e+00 0.00000e+00 1.00000e+00]]
delta_mat_mct -> delta_mat_lidar
[[ 9.99725450e-01 -2.34404500e-02 4.44664099e-04 -9.38036435e-02][ 2.34394500e-02 9.99723550e-01 2.28772378e-03 1.40585449e-01][-4.98284007e-04 -2.27668585e-03 9.99999000e-01 -6.17034358e-03][ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
2.变换矩阵左右乘/旋转矩阵左右乘
与变换某个目标不同,当一个坐标系发生连续变化时,如何描述这个坐标系的最终变换。
例如,先绕x轴顺时针转180度,然后绕z轴顺时针转45,最后绕y轴转30°
这个时候就会出现两种情况:
1.原始坐标系称为a0,先绕x轴(a0的x轴)顺时针转180度得到坐标系a1,然后绕z轴(这个z轴是a0的z轴)顺时针转45得到坐标系a2,最后绕y轴(这个y轴是a0的y轴)转30°
2.原始坐标系称为a0,先绕x轴(a0的x轴)顺时针转180度得到坐标系a1,然后绕z轴(这个z轴是a1的z轴)顺时针转45得到坐标系a2,最后绕y轴(这个y轴是a2的y轴)转30°
也就是,绕固定坐标系旋转还是绕自身坐标系旋转
此时有个口诀
!!!左乘旋转矩阵绕固定坐标系旋转,右乘旋转矩阵绕自身坐标系旋转!!!
在泊车项目中,一般都是按照平面处理的,也就是旋转的变化都是绕Z轴,因为无论是固定为初始坐标系还是自身坐标系Z轴都是不变的,因此,左乘右乘都可以。
但是上述仅仅是理想情况。
一般情况下都不是纯z轴变化,此时,就要区分是左乘还是右乘。
2.1右乘
2.1.1例如:求取外参【imu到lidar的外参】
已知:
前后左右上下,分别表示车体的前后左右上下
imu坐标系:X朝前,Y朝右,Z朝下
lidar坐标系:X朝右前45度,Y朝左前45度,Z朝上
lidar坐标系中心到imu坐标系中心在车体系下的相对位置关系为:
t X l i d a r − i m u c a r = 1.59 tX_{lidar-imu}^{car}=1.59 tXlidar−imucar=1.59
t Y l i d a r − i m u c a r = − 0.5 tY_{lidar-imu}^{car}=-0.5 tYlidar−imucar=−0.5
t Z l i d a r − i m u c a r = 0.66 tZ_{lidar-imu}^{car}=0.66 tZlidar−imucar=0.66
从imu系到lidar系的变化可以归结为以下几步:
- 绕x轴顺时针旋转180度 =R1
- 绕z轴顺时针旋转45度 =R2
- 计算旋转矩阵R3=R2*R1
(此处计算R1*R2的结果是不一样的,虽然绕x轴顺时针旋转180度,z轴与原始z轴重合,但是这两个z轴朝向不同,因此在顺逆时针的旋转向量表达也会不同) - 计算车体系下的偏移量T{tX,tY,tZ}到lidar系的分量
t X l i d a r − i m u l i d a r = 1.47 tX_{lidar-imu}^{lidar}=1.47 tXlidar−imulidar=1.47
t Y l i d a r − i m u l i d a r = 0.77 tY_{lidar-imu}^{lidar}=0.77 tYlidar−imulidar=0.77
t Z l i d a r − i m u l i d a r = 0.66 tZ_{lidar-imu}^{lidar}=0.66 tZlidar−imulidar=0.66 - 将旋转R3和t结合得到T
过程如下:
R 3 = R 2 ∗ R 1 R_3=R_2*R_1 R3=R2∗R1
R 3 = [ c o s ( 45 ∗ π / 180 ) − s i n ( 45 ∗ π / 180 ) 0 s i n ( 45 ∗ π / 180 ) c o s ( 45 ∗ π / 180 ) 0 0 0 1 ] [ 1 0 0 0 c o s ( 180 ∗ π / 180 ) − s i n ( 180 ∗ π / 180 ) 0 s i n ( 180 ∗ π / 180 ) c o s ( 180 ∗ π / 180 ) ] R_3=\begin{bmatrix} cos(45*\pi/180) & -sin(45*\pi/180) & 0 \\ sin(45*\pi/180) & cos(45*\pi/180) & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(180*\pi/180) & -sin(180*\pi/180) \\ 0 & sin(180*\pi/180) & cos(180*\pi/180) \end{bmatrix} R3= cos(45∗π/180)sin(45∗π/180)0−sin(45∗π/180)cos(45∗π/180)0001 1000cos(180∗π/180)sin(180∗π/180)0−sin(180∗π/180)cos(180∗π/180)
R 3 = [ ( 2 ) / 2 − ( 2 ) / 2 0 ( 2 ) / 2 ( 2 ) / 2 0 0 0 1 ] [ 1 0 0 0 − 1 0 0 0 − 1 ] R_3=\begin{bmatrix} \sqrt(2)/2 & -\sqrt(2)/2 & 0 \\ \sqrt(2)/2 & \sqrt(2)/2 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix} R3= (2)/2(2)/20−(2)/2(2)/20001 1000−1000−1
R 3 = [ ( 2 ) / 2 ( 2 ) / 2 0 ( 2 ) / 2 − ( 2 ) / 2 0 0 0 1 ] R_3=\begin{bmatrix} \sqrt(2)/2 & \sqrt(2)/2 & 0 \\ \sqrt(2)/2 &-\sqrt(2)/2 & 0 \\ 0 & 0 & 1 \end{bmatrix} R3= (2)/2(2)/20(2)/2−(2)/20001
PS:有的时候是从imu+gnss得到的结果,此时结果为经纬度+高程+航向角的结果,如果是按照经纬度是无法直接使用的需要转到mct(墨卡托)坐标系下,此时外参就不是从imu到lidar了,而是从mct到lidar。因为从gnss的坐标系到mct坐标系已经经历过一轮变换了,此时需要注意的是gnss坐标系输出的航向角heading是顺时针还是逆时针,这个heading(yaw)角需要与mct坐标系下的heading保持一致。
2.1.2例如: 累计 δ P o s e \delta Pose δPose得到每一个时刻的Pose
T 1 = T 0 ∗ δ T 0 1 T_1=T_0*\delta T_0^1 T1=T0∗δT01
T 2 = T 1 ∗ δ T 1 2 T_2=T_1*\delta T_1^2 T2=T1∗δT12
T n = T n − 1 ∗ δ T n − 1 n T_n=T_{n-1}*\delta T_{n-1}^n Tn=Tn−1∗δTn−1n
T n = T 0 ∗ δ T 0 1 ∗ δ T 1 2 … … ∗ δ T n − 1 n T_n=T_0*\delta T_0^1*\delta T_1^2……*\delta T_{n-1}^n Tn=T0∗δT01∗δT12……∗δTn−1n
2.1.3例如: 从imuPP(pose&postion)得到lidarPP(pose&postion)
已知外参:
E x t r i n s i c = T i m u l i d a r Extrinsic=T_{imu}^{lidar} Extrinsic=Timulidar
P P l i d a r = P P i m u ∗ T i m u l i d a r PP_{lidar}=PP_{imu}*T_{imu}^{lidar} PPlidar=PPimu∗Timulidar
PS:一般情况下imu的位姿矩阵会被理解为用多个空间3维点组成的轨迹,但其实不然,这个PP是有方向的,所以不能当成点/点云处理,而是当作变换矩阵处理(当前PP与世界初始坐标系原点的变换矩阵)。
又因为外参是相对自己坐标系的变换而不是相对世界初始坐标系(固定坐标系),所以外参也是用的右乘。
PS:
虽然此处的imupose可以看作是一个旋转位移增量矩阵,但是!!此处不是坐标系发生变换,与1.3的例子不同。此处是同一个坐标系下,imu轨迹和lidar轨迹存在一个刚性变换关系。同一个mct坐标系下,imupose和lidarpose的变换关系。
2.2左乘
暂时没有例子
相关文章:

debug过程中,矩阵左乘右乘相关概念梳理
1. 变换点或者变换向量 1.1左乘 矩阵左乘通常是指对”目标点“进行左乘,即: A ′ R ∗ A AR*A A′R∗A 其中,A为原始3维点,表示一个3*1的列向量,R为33的旋转矩阵,A‘为变换后的点 B ′ T ∗ B BT*B B′T∗B 其中…...
Ubuntu 安装Kafka
在本指南中,我们将逐步演示如何在 Ubuntu 22.04 上安装 Apache Kafka。 在大数据中,数以百万计的数据源生成了大量的数据记录流,这些数据源包括社交媒体平台、企业系统、移动应用程序和物联网设备等。如此庞大的数据带来的主要挑战有两个方面…...

洗地机性价比高的是哪款?高性价比洗地机排名
洗地机已成为当下备受欢迎的智能家电之一,但在挑选合适的洗地机时,面对各种新词汇和功能选择,可能会让人感到困惑。因此,为了帮助大家在购买洗地机时不踩坑,我们基于市面上主流品牌的综合分析对比,总结出来…...

安装konga
创建konga数据库 docker run --rm pantsel/konga:latest -c prepare -a postgres -u postgresql://kong:kong{IP}:5432/konga这里要注意docker部署时IP不能直接访问localhost 安装konga docker run -p 1337:1337 \--network kong-net \--name konga \-e "NODE_ENVprodu…...

算法基础之高精度总结
目录 高精度算法分类 高精度加减乘除的异同点 加和乘 相同点 减和除 相同点 不同点 处理前导0的方式 高精度算法分类 分类:加、减、乘、除 其中加减乘都适用于两个数都是高精度,除法因为除数是高精度的话不好用整除的方法,所以除法时…...
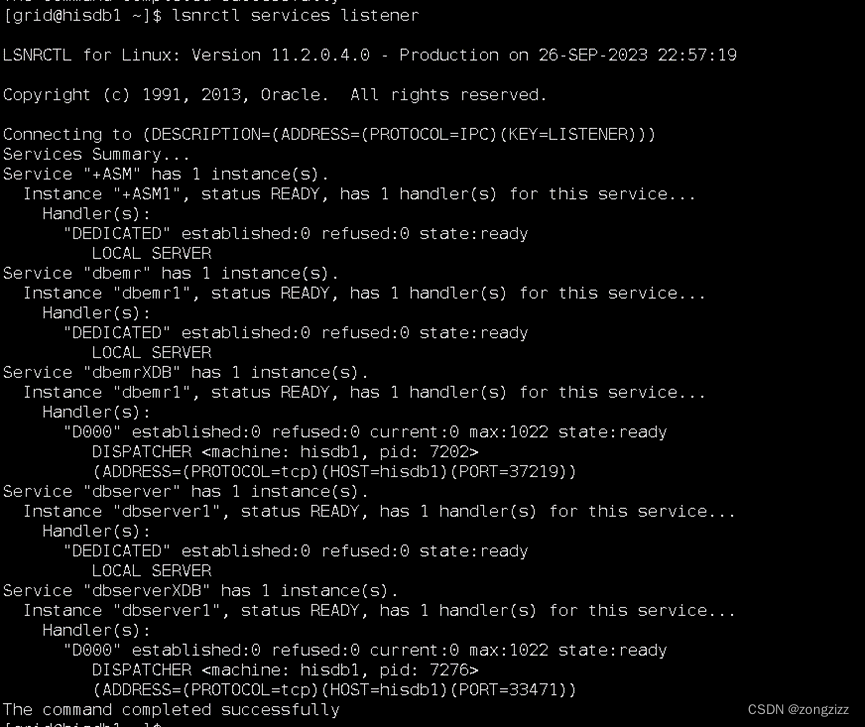
oracle TNS Listener 远程投毒漏洞修复
有个客户在等保测评过程,测评公司扫出一个关于oracle的漏洞如下: 客户是RAC环境11.2.0.4,在生产修复漏洞前我做了如下测试验证: 测试环境准备: RAC一套11.2.0.4 实例名dbserver [oraclehisdb1 ~]$ cat /etc/hosts …...
)
第二章:最新版零基础学习 PYTHON 教程(第一节 - Python 输入/输出–在 Python 中获取输入)
开发人员经常需要与用户交互,以获取数据或提供某种结果。如今,大多数程序都使用对话框来要求用户提供某种类型的输入。而Python为我们提供了两个内置函数来读取键盘输入。 目录 输入(提示) raw_input(提示) 输入函数在 Python 中的工作原理:...
react create-react-app v5 从零搭建项目
前言: 好久没用 create-react-app做项目了,这次为了个h5项目,就几个页面,决定自己搭建一个(ps:mmp 好久没用,搭建的时候遇到一堆问题)。 我之前都是使用 umi 。后台管理系统的项目 使用 antd-…...
2023软件测试八股文,涵盖所有面试题
Part1 1、你的测试职业发展是什么? 测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前3年积累测试经验,按如何做好测试工程师的要点去要求自…...

性能压力测试的定义及步骤是什么
在今天的数字化时代,软件系统的性能和稳定性对于企业的成功至关重要。为了确保软件在高负载和压力情况下的正常运行,性能压力测试成为了不可或缺的环节。本文将介绍性能压力测试的定义、步骤。 一、性能压力测试的定义和目标 性能压力测试是通过模拟实际…...

Selenium自动化中处理鼠标悬停并操作的方法
因为测试中遇到要鼠标悬停显示Tooltip,并操作tip上的内容,现记录如下。 方法一:通过鼠标链式操作 from selenium.webdriver.common.action_chains import ActionChains as ACac AC(self.driver)lst self.driver.find_element_by_xpath(//…...

python socket 编程实现猜数字
项目地址 https://gitee.com/lmk73444/learn_spring/tree/master/doc/1_x%E5%AD%A6%E4%B9%A0/002_py_socket python socket试验 mkdir /root/git_proj cd /root/git_proj# 首次 clone 项目 git clone https://gitee.com/lmk73444/learn_spring.git# 非首次 # 更新项目 cd /ro…...
20个提升效率的JS简写技巧,告别屎山!
JavaScript 中有很多简写技巧,可以缩短代码长度、减少冗余,并且提高代码的可读性和可维护性。本文将介绍 20 个提升效率的 JS 简写技巧,助你告别屎山,轻松编写优雅的代码! 移除数组假值 可以使用 filter() 结合 Bool…...
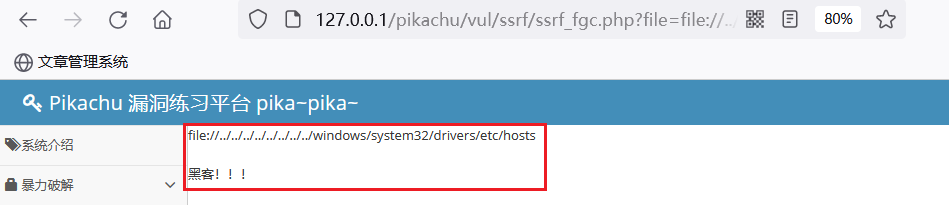
Pikachu靶场——SSRF 服务端请求伪造
文章目录 1 SSRF 服务端请求伪造1.1 SSRF(curl)1.1.1 漏洞防御 1.2 SSRF(file_get_content)1.2.1 漏洞防御1.2.3 SSRF 防御 1 SSRF 服务端请求伪造 SSRF(Server-Side Request Forgery:服务器端请求伪造) 其形成的原因大都是由于服务端提供了从其他服务器应用获取数据的功能&a…...

Android file
写文件——FileOutputStream openFileOutput 读文件——FileInputStream openFileInput openFileOutput写文件时当文件不存在,Android自动创建。 通过BufferedWriter直接写入字符串 public void writeFile(String inputText) {FileOutputStream outputStream nul…...

【计算机网络】计网常见面试题总结
目录 一、谈一谈对OSI七层模型和TCP/IP四层模型的理解? 二、谈一谈TCP协议的三次握手过程? 三、TCP协议为什么要三次握手?两次、四次不行吗? 四、谈一谈TCP协议的四次挥手过程? 五、什么是流量控制? …...

SpringMVC 学习(七)JSON
9. JSON 9.1 简介 JSON(JavaScript Object Notation,JS 对象标记)是一种轻量级数据交换格式,采用独立于编程语言的文本格式储存和表示数据,易于机器解析和生成,提升网络传输效率。 任何 JavaScript 支持…...
重学C++ | std::set 的原理
std::set 是C标准库中的容器之一,它基于红黑树实现。std::set 利用红黑树的特性来实现有序的插入、查找和删除操作,并且具有较好的平均和最坏情况下的时间复杂度。 当向 std::set 插入元素时,它会按照特定的比较函数(bool less<…...

AnV-X6使用及总结
目录 1 简介2 安装3 基础概念3.1 画布Graph3.2 基类Cell3.3 节点Node3.4 边Edge 4 使用4.1 创建节点4.2 节点连线4.3 事件系统 5 总结 1 简介 AntV是一个数据可视化(https://x6.antv.antgroup.com/)的工具(https://antv.vision/zh/ …...

Go 围炉札记
文章目录 一、安装二、文档三、使用 一、安装 VSCode 和 CLion 为 Go 开发配置Visual Studio Code | Microsoft Learn VScode下配置Go语言开发环境【2023最新】 基础篇:新手使用vs code新建go项目 vscode里安装Go插件和配置Go环境 GO 笔记 Golang 配置代理 golang…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
