Spring Boot 集成 MinIO 实现文件上传、下载和删除
MinIO 是一种开源的对象存储服务,它基于云原生架构构建,并提供了高性能、易于扩展和安全的存储解决方案。
一.安装和配置 MinIO 服务器
为了演示方便,本文采用Windows安装
1.在官方网站下载MinIO 安装文件,地址:https://dl.minio.org.cn/server/minio/release/windows-amd64/minio.exe;
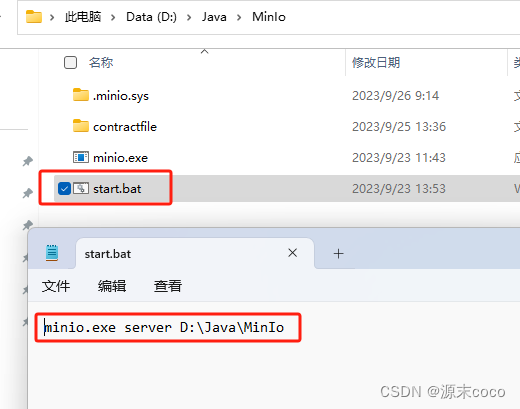
2.在minio.exe目录下创建start.bat配置启动文件:"D:\Java\MinIo"是服务启动时文件存放的位置
minio.exe server D:\Java\MinIo3.双击minio.exe文件启动
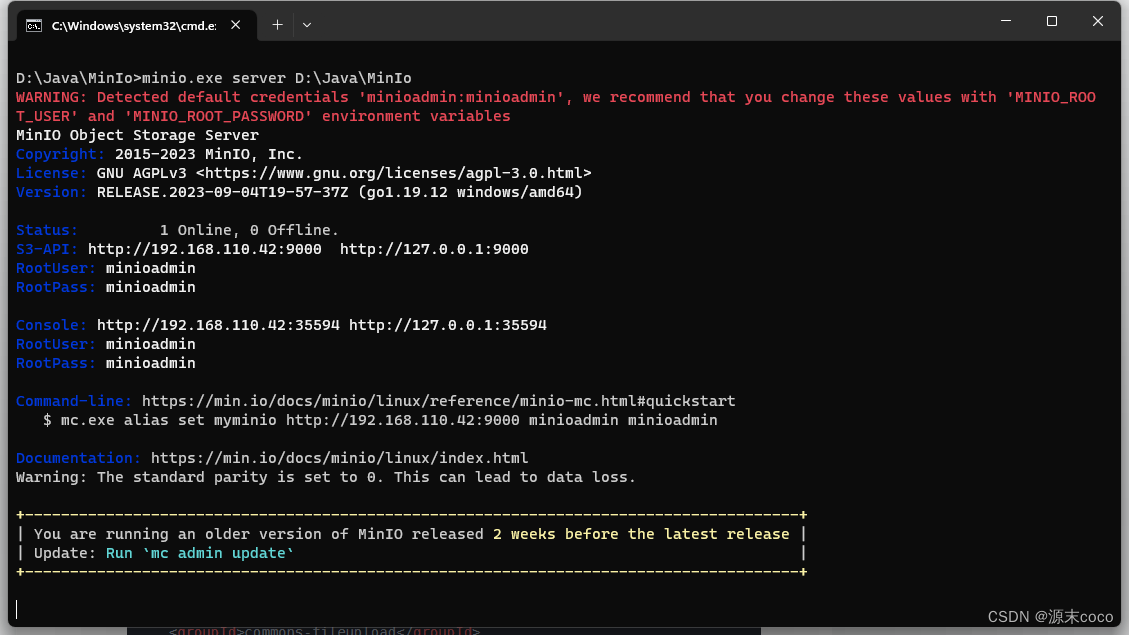
4.创建一个 Spring Boot 项目
1.创建一个 Spring Boot 项目
2.添加依赖,注意依赖版本
<!--文件上传-->
<dependency><groupId>commons-io</groupId><artifactId>commons-io</artifactId><version>2.4</version>
</dependency>
<dependency><groupId>commons-fileupload</groupId><artifactId>commons-fileupload</artifactId><version>1.4</version>
</dependency><!--MinIO对象存储-->
<dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.4.3</version>
</dependency>
<dependency><groupId>com.squareup.okhttp3</groupId><artifactId>okhttp</artifactId><version>4.8.1</version>
</dependency>二.配置文件
1.yaml配置文件
#MinIO配置
minio:endpoint: http://127.0.0.01:9000 #连接地址accessKey: minioadmin#账号 默认minioadminsecretKey: minioadmin#密码 默认minioadminbucketName: contractfile #桶名 存放合同文件 桶名校验规则:!name.matches("^[a-z0-9][a-z0-9\\.\\-]+[a-z0-9]$")2.配置类,用来连接Minio
@Data
@Configuration
@ConfigurationProperties(prefix = "minio")
public class MinioConfig {//连接地址private String endpoint;//账号 默认minioadminprivate String accessKey;//密码 默认minioadminprivate String secretKey;@Beanpublic MinioClient minioClient() {MinioClient minioClient = MinioClient.builder().endpoint(endpoint).credentials(accessKey, secretKey).build();return minioClient;}}3.工具类,用来操作文件
@Slf4j
@Component
public class MinioUtils {@Autowiredprivate MinioClient minioClient;@Value("${minio.bucketName}")private String bucketName;/*** 操作文件时先创建Bucket* 如果没有Bucket则创建** @param bucketName*/@SneakyThrows(Exception.class)public void createBucket(String bucketName) {if (!bucketExists(bucketName)) {minioClient.makeBucket(MakeBucketArgs.builder().bucket(bucketName).build());}}/*** 判断Bucket是否存在,true:存在,false:不存在** @param bucketName* @return*/@SneakyThrows(Exception.class)public boolean bucketExists(String bucketName) {return minioClient.bucketExists(BucketExistsArgs.builder().bucket(bucketName).build());}/*** 判断文件是否存在** @param bucketName* @param fileRealName* @return*/public boolean isObjectExist(String bucketName, String fileRealName) {boolean exist = true;try {minioClient.statObject(StatObjectArgs.builder().bucket(bucketName).object(fileRealName).build());} catch (Exception e) {log.error("[Minio工具类]>>>> 判断文件是否存在, 异常:", e);exist = false;}return exist;}/*** 使用MultipartFile进行文件上传** @param bucketName 存储桶* @param file 文件* @param fileRealName 文件名* @return 文件下载外链*/@SneakyThrows(Exception.class)public String uploadFile(String bucketName, MultipartFile file, String fileRealName) {createBucket(bucketName);InputStream inputStream = file.getInputStream();minioClient.putObject(PutObjectArgs.builder().bucket(bucketName).object(fileRealName).contentType(file.getContentType()).stream(inputStream, inputStream.available(), -1).build());GetPresignedObjectUrlArgs args = GetPresignedObjectUrlArgs.builder().bucket(bucketName).object(fileRealName).method(Method.GET).build();return minioClient.getPresignedObjectUrl(args);}/*** 删除文件** @param bucketName 存储桶* @param fileRealName 文件名称*/@SneakyThrows(Exception.class)public void removeFile(String bucketName, String fileRealName) {createBucket(bucketName);minioClient.removeObject(RemoveObjectArgs.builder().bucket(bucketName).object(fileRealName).build());}/*** 下载文件** @param httpServletResponse httpServletResponse* @param fileRealName 文件存储名称* @param fileName 文件下载名称* @throws IOException IOException*/public void downloadFile(String bucketName, String fileRealName, String fileName, HttpServletResponse httpServletResponse) throws Exception {createBucket(bucketName);//获取文件流InputStream inputStream = minioClient.getObject(GetObjectArgs.builder().bucket(bucketName).object(fileRealName).build());//设置响应头信息,告诉前端浏览器下载文件httpServletResponse.setContentType("application/octet-stream;charset=UTF-8");httpServletResponse.setCharacterEncoding("UTF-8");httpServletResponse.setHeader("Content-Disposition", "attachment;filename=" + URLEncoder.encode(fileName, "UTF-8"));//获取输出流进行写入数据OutputStream outputStream = httpServletResponse.getOutputStream();// 将输入流复制到输出流byte[] buffer = new byte[4096];int bytesRead = -1;while ((bytesRead = inputStream.read(buffer)) != -1) {outputStream.write(buffer, 0, bytesRead);}// 关闭流资源inputStream.close();outputStream.close();}
}相关文章:

Spring Boot 集成 MinIO 实现文件上传、下载和删除
MinIO 是一种开源的对象存储服务,它基于云原生架构构建,并提供了高性能、易于扩展和安全的存储解决方案。 一.安装和配置 MinIO 服务器 为了演示方便,本文采用Windows安装 1.在官方网站下载MinIO 安装文件,地址:ht…...
Polygon Miden交易模型:Actor模式 + ZKP => 并行 + 隐私
1. 引言 前序博客: Polygon Miden:扩展以太坊功能集的ZK-optimized rollupPolygon Miden zkRollup中的UTXO账户混合状态模型 Polygon Miden为: ZK-optimized rollup由客户端生成证明完善Polygon ZK系列解决方案,致力于成为网络…...
)
Java流的体系结构(二)
文章目录 一、对象流的使用1.概念2.序列化机制3.代码案例:序列化过程:将内存中的java对象保存到磁盘中或通过通络传输出去4.反序列化,将磁盘文件中的对象还原为内存中的一个java对象 二、RandomAccessFile的使用1.说明2.代码案例 提示&#x…...

python计算阶层
阶层(Factorial)是指从1到一个正整数n的所有整数相乘,即n! 1 2 3 … n。下面是Python代码计算阶层: def factorial(n):"""计算阶层:param n: 正整数:return: n的阶层"""if n 1 or n 0:retu…...

前端架构师之01_ES6_基础
1 初识ES6 简单来说,ECMAScript是JavaScript语言的国际标准,JavaScript是实现ECMAScript标准的脚本语言。 2011年,ECMA国际标准化组织在发布ECMAScript 5.1版本之后,就开始着手制定第6版规范。 存在的问题:这个版本…...

银行卡号识别
# 导入工具包 from imutils import contours import numpy as np import argparse import cv2 import myutils# 设置参数 # ap = argparse.ArgumentParser() # ap.add_argument("-i", "--image", required=True, # help="path to input image")…...
【Idea】idea、datagrip设置输入法
https://github.com/RikudouPatrickstar/JetBrainsRuntime-for-Linux-x64/releases/tag/jbr-release-17.0.6b829.5https://github.com/RikudouPatrickstar/JetBrainsRuntime-for-Linux-x64/releases/tag/jbr-release-17.0.6b829.5 下载后解压并重命名为 jbr, 然后替换对应 ide…...

回归预测 | MATLAB实现基于RF-Adaboost随机森林结合AdaBoost多输入单输出回归预测
回归预测 | MATLAB实现基于RF-Adaboost随机森林结合AdaBoost多输入单输出回归预测 目录 回归预测 | MATLAB实现基于RF-Adaboost随机森林结合AdaBoost多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现基于RF-Adaboost随机森林结合…...
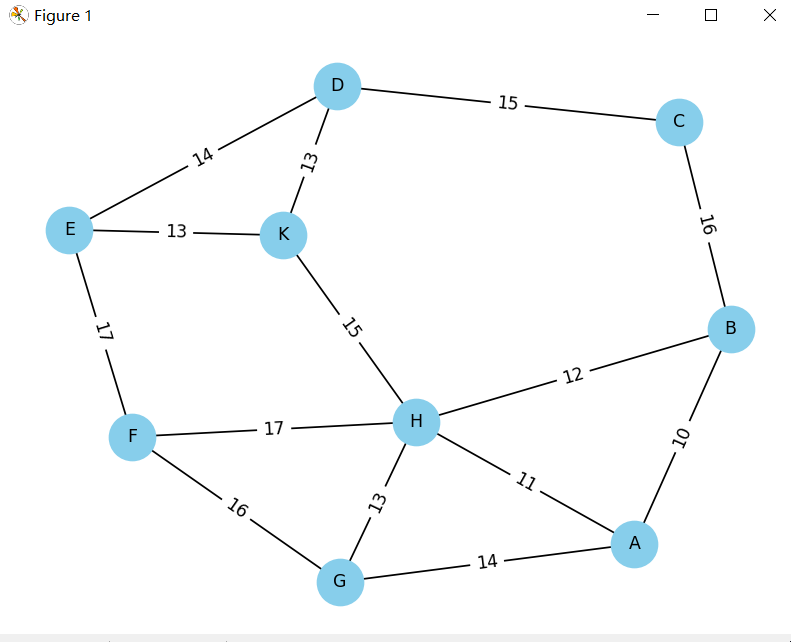
最小生成树 | 市政道路拓宽预算的优化 (Minimum Spanning Tree)
任务描述: 市政投资拓宽市区道路,本着执政为民,节省纳税人钱的目的,论证是否有必要对每一条路都施工拓宽? 这是一个连问带答的好问题。项目制学习可以上下半场,上半场头脑风暴节省投资的所有可行的思路&a…...
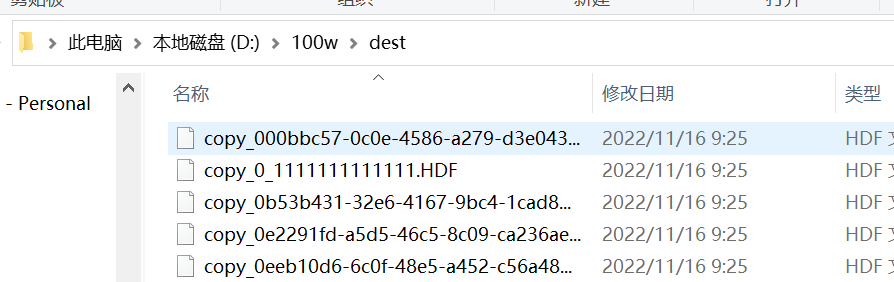
Java实现使用多线程,实现复制文件到另一个目录,起不一样的名字,创建100万个数据
目录 1 需求2 实现 1 需求 我现在有一个300MB 的文件,想要根据这个文件,创建100万个大小一样的,名称不一样,如何实现,如何比较快点实现 2 实现 1 先准备好这个文件 2 准备好目录 3 写代码 private static void crea…...
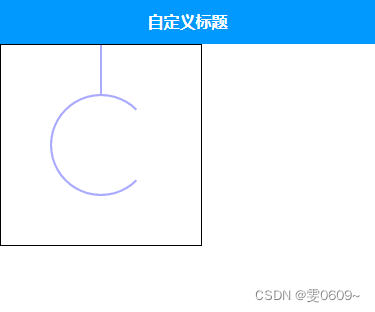
uni-app:canvas-图形实现1
效果 代码 <template><view><!-- 创建了一个宽度为300像素,高度为200像素的canvas元素。canvas-id属性被设置为"firstCanvas",可以用来在JavaScript中获取该canvas元素的上下文对象。 --><canvas style"width:200p…...
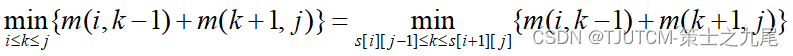
【算法分析与设计】动态规划(下)
目录 一、最长公共子序列1.1 最长公共子序列的结构1.2 子问题的递归结构1.3 计算最优值1.4 举例说明1.5 算法的改进 二、最大子段和2.1 代码2.2 最大子段和问题的分治算法2.3 代码2.4 分治算法的时间复杂度2.5 最大子段和问题的动态规划算法 三、凸多边形最优三角剖分3.1 三角剖…...
计算机图像处理-均值滤波
均值滤波 线性滤波器的原始数据与滤波结果是一种算术运算,即用加减乘除等运算实现,如均值滤波器(模板内像素灰度值的平均值)、高斯滤波器(高斯加权平均值)等。由于线性滤波器是算术运算,有固定…...
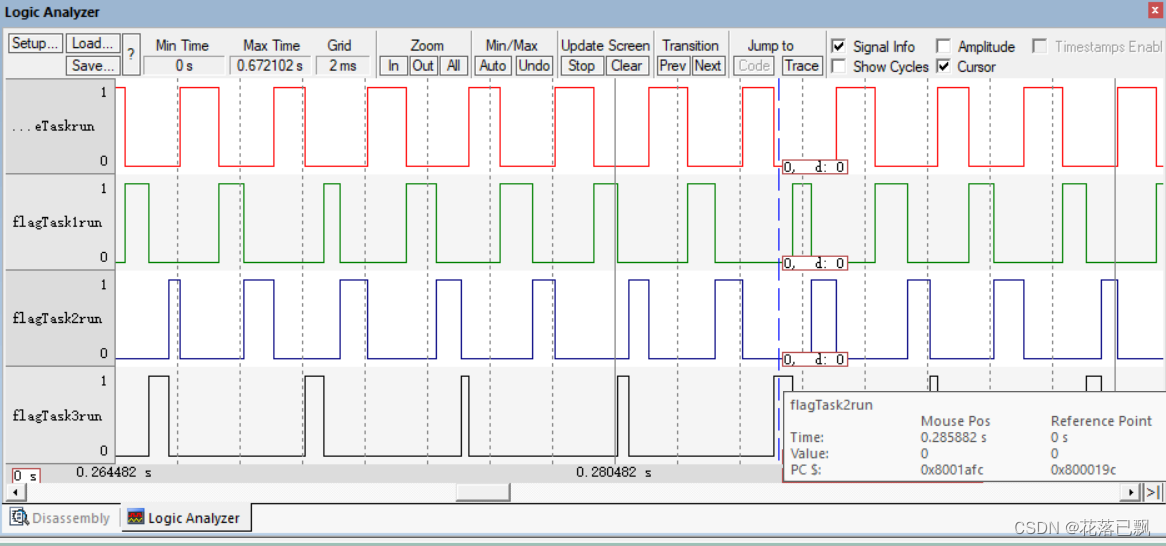
FreeRTOS入门教程(空闲任务和钩子函数及任务调度算法)
文章目录 前言一、空闲任务概念二、钩子函数概念三、任务调度算法四、任务调度算法实验1.实验代码2.是否抢占3.时间片是否轮转4.空闲任务让步 总结 前言 本篇文章将带大家学习一下什么是空闲任务以及钩子函数,以及学习FreeRTOS中的任务调度算法,了解在F…...

Javascript真的是10天内做出来的吗?
我曾听说,Javascript 之所以有这么多缺点,是因为它的第一个版本是在短短十天内完成的。我很好奇:1)这是否属实;2)这是否能解释这种语言的缺陷。 经过一番研究,我可以不自信地说:是的…...

picoctf_2018_got_shell
picoctf_2018_got_shell Arch: i386-32-little RELRO: Partial RELRO Stack: No canary found NX: NX enabled PIE: No PIE (0x8048000)32位,只开了NX int __cdecl __noreturn main(int argc, const char **argv, const char **envp) {_DWOR…...

作用域 CSS 回来了
几年前,消失的作用域 CSS,如今它回来了,而且比以前的版本要好得多。 更好的是,W3C规范基本稳定,现在Chrome中已经有一个工作原型。我们只需要社区稍微关注一下,引诱其他浏览器构建它们的实现,并…...
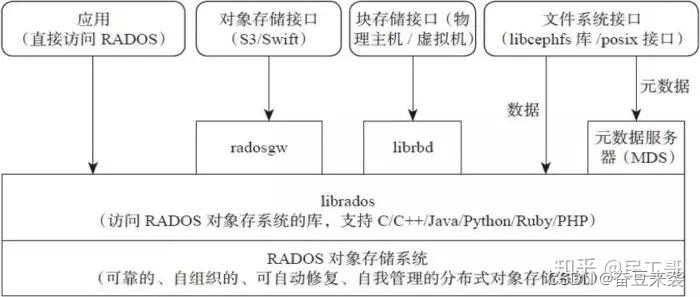
简述ceph文件储存系统
Ceph 是一个统一的分布式存储系统和共享机制,它定义了数据如何存储在一个或多个节点上并呈现给其他机器以供文件访问。 Ceph特点 高性能 a. 摒弃了传统的集中式存储元数据寻址的方案,采用CRUSH算法,数据分布均衡,并行度高。 b.考…...

计算机图像处理:椒盐噪声和高斯噪声
图像滤波 图像滤波,即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,同时会造成图像一定程度上的模糊,这也叫做平滑或者低通滤波。无论是均衡化直方图和图像滤波,都一定程度上降低了图像阈值分割的难度,直…...

SQL SELECT 子查询与正则表达式
在之前的文章中已经探讨了 SQL SELECT 语句的基础和进阶用法,以及如何通过高级技巧来进行更复杂的数据查询和分析。本文将介绍 SQL SELECT 语句中的子查询和正则表达式的使用。这些是 SQL 中非常强大的工具,能让您进行更复杂和精细的数据操作。 文章目录 子查询基础与应用子…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
