统计模型----决策树
决策树
(1)决策树是一种基本分类与回归方法。它的关键在于如何构建这样一棵树。决策树的建立过程中,使用基尼系数来评估节点的纯度和划分的效果。基尼系数是用来度量一个数据集的不确定性的指标,其数值越小表示数据集的纯度越高。决策树的节点划分方式可以根据不同的算法和参数设置而不同。节点划分方式不同,但是基尼系数的下降效果却是一样的,只是具体数值不同。决策树的深度可以根据需求进行设置,如果不限制决策树的深度,它将一直延伸下去,直到所有叶子节点的均方误差为0。
模型特点:优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配的问题
适用数据类型:数值型和标称型
(3)决策树通常有三个步骤:特征选择、决策树的生成、决策树的修剪。
(4)决策树的构造
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分,也对应着决策树的构建。
1)开始:构建根节点,将所有训练数据都放在根节点,选择一个最优特征,按着这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下最好的分类。
2)如果这些子集已经能够被基本正确分类,那么构建叶节点,并将这些子集分到所对应的叶节点去。
3)如果还有子集不能够被正确的分类,那么就对这些子集选择新的最优特征,继续对其进行分割,构建相应的节点,如果递归进行,直至所有训练数据子集被基本正确的分类,或者没有合适的特征为止。
4)每个子集都被分到叶节点上,即都有了明确的类,这样就生成了一颗决策树。
(5)决策树分析举例(理解)
例如:小熊毕业了来到一家银行工作,刚刚入行的小熊仔细整理了客户的基本信息。如下图
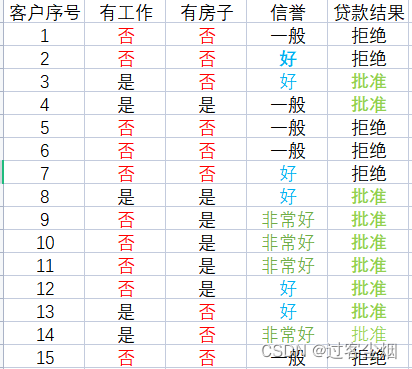

小熊根据以上信息得出基本结论:
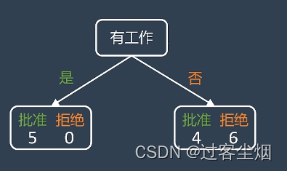
(1)按有工作分类:
(2)按信誉分类的话:
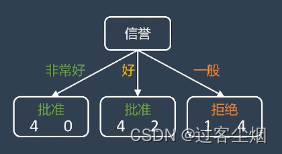
以上样本结果好像与数据结果相悖
那如果按有工作和信誉因素分类的话:
如果客户有工作那就可以批准贷款,如果客户没有工作的话,我们再考虑他的信誉情况做出判断,这就是利用决策树进行分类的过程。
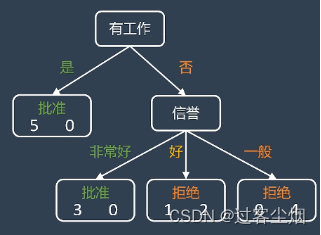
标准可以用一个基尼系数来定义:
采用基尼系数进行运算的决策树也称为CART决策树。
基尼系数(gini)用于计算一个系统中的失序现象,即系统的混乱程度(纯度)。基尼系数越高,系统的混乱程度就越高(不纯),建立决策树模型的目的就是降低系统的混乱程度(体高纯度),从而得到合适的数据分类效果。
基尼系数的计算公式如下:
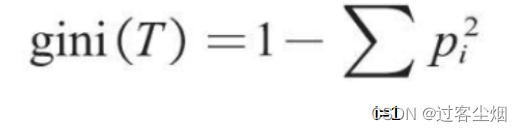
选择基尼数最小的来作为决策树下一级的标准。
Gini= 1-p(批准)2-p(拒绝)2
当p(批准)=1 p(拒绝)=0 Gini=1-1=0
当p(批准)=0 p(拒绝)=1 Gini=1-0-1=0
当p(批准)=0.5 p(拒绝)=0.5 Gini=1-0.25-0.25=0.5
以以上例子可以得出
Gini= 1-p(9/15)2-p(6/15)2=0.48
Gini(工作,是)=1-(5/5)-0=0
Gini(工作,否)=1-(4/10)-(6/10)=0.48
Gini(工作)=5/15Gini(工作,是)+10/15Gini(工作,否)=0.32
依次算出:Gini(房子)=0.27 Gini(信誉)=0.28
以上可知有房子的基尼系数最小,所以依此为下一次分类的依据:
相关文章:
统计模型----决策树
决策树 (1)决策树是一种基本分类与回归方法。它的关键在于如何构建这样一棵树。决策树的建立过程中,使用基尼系数来评估节点的纯度和划分的效果。基尼系数是用来度量一个数据集的不确定性的指标,其数值越小表示数据集的纯度越高。…...

C# List 复制之深浅拷贝
C# List 复制 之深浅拷贝 声明类 public class TestStu{public int Number{get;set; }public string Name{get;set; }}public static async Task<int> Main(string[] args){var stu1 new TestStu(){Number 1,Name "1"};var stu2 new TestStu(){Numbe…...
)
论<script> 标签可以直接写在 HTML 文件中的哪些位置?(可以将 <script> 标签直接插入到 HTML 文件的任何位置)
可以将 <script> 标签直接插入到 HTML 文件的任何位置,以在相应位置执行 JavaScript 代码。 以下是几个示例: 1.<head> 元素内部:在 <head> 元素内部放置 <script> 标签时,脚本将在页面加载过程中被下载和…...
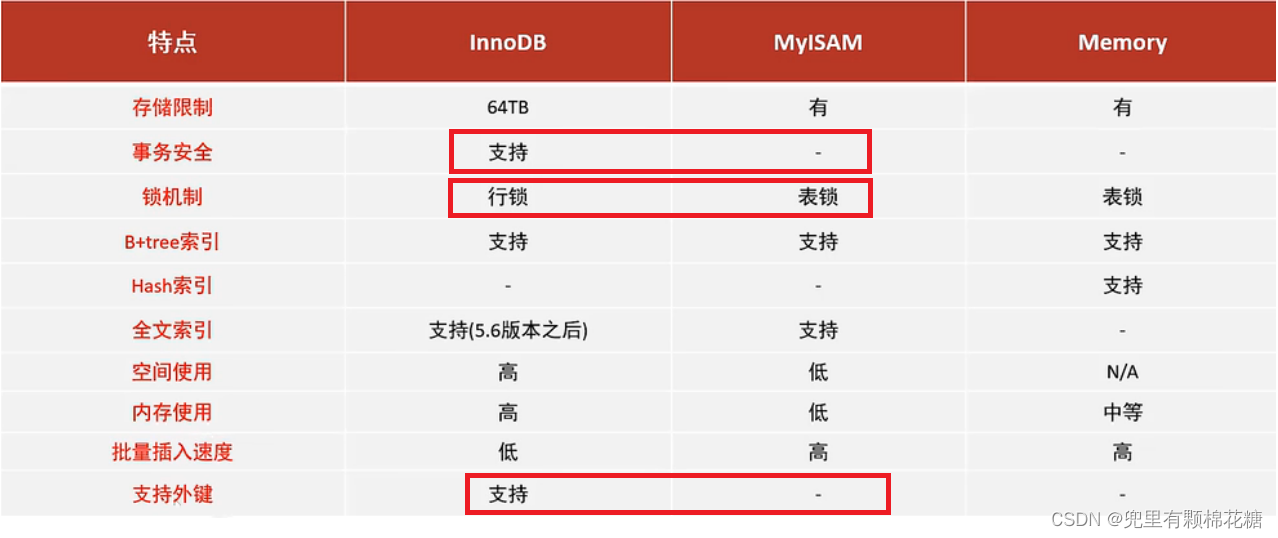
【MySQL进阶】--- 存储引擎的介绍
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【MySQL学习专栏】🎈 本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌 目录 一、什么…...
self-XSS漏洞SRC挖掘
本文由掌控安全学院 - 一朵花花酱 投稿 Markdown是一种轻量级标记语言,创始人为约翰格鲁伯(John Gruber)。它允许人们使用易读易写的纯文本格式编写文档,然后转换成有效的 XHTML(或者HTML)文档。这种语言吸…...

1859. 将句子排序
目录 一、题目 二、代码 一、题目 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 二、代码 定义了一个vector<vector<string>> v(MAX);采用const string& word : v[k] word 就会依次取得 v[k] 中的每个元素(v[k][0],…...
普通学校,普通背景,普通公司,不普通总结。
作者:阿秀 InterviewGuide大厂面试真题网站:https://top.interviewguide.cn 这是阿秀的第「313」篇原创 小伙伴们大家好,我是阿秀。 可能很多人点开牛客、知乎、B站,一看帖子的标题都是"某985xxxx"、"不入流211xxx…...
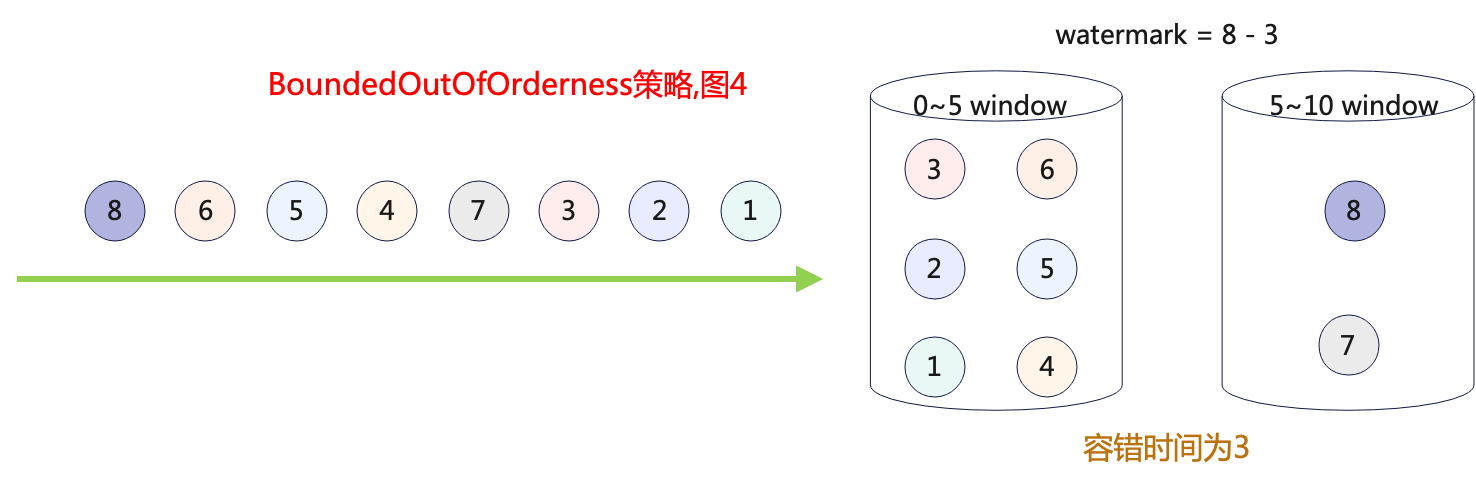
Flink之Watermark生成策略
在Flink1.12以后,watermark默认是按固定频率周期性的产生. 在Flink1.12版本以前是有两种生成策略的: AssignerWithPeriodicWatermarks周期性生成watermarkAssignerWithPunctuatedWatermarks[已过时] 按照指定标记性事件生成watermark 新版本API内置的watermark策略 单调递增的…...

提升API文档编写效率,Dash for Mac是你的不二之选
在编写和开发API文档的过程中,你是否经常遇到查找困难、管理混乱、效率低下等问题?这些都是让人头疼的问题,但现在有了Dash for Mac,一切都将变得简单而高效。 Dash for Mac是一款专为API文档编写和管理设计的工具,它…...

无人注意,新安装的 Ubuntu 23.04 不支持安装 32 位应用
导读新安装的 Ubuntu 23.04 不支持安装 32 位应用。 无人注意,新安装的 Ubuntu 23.04 不支持安装 32 位应用 有用户报告,在新安装的 Ubuntu 23.04 上从 Ubuntu 仓库安装的 Steam 客户端是不工作的。在 Ubuntu 23.04 中使用了基于 Flutter 的新安装程序…...
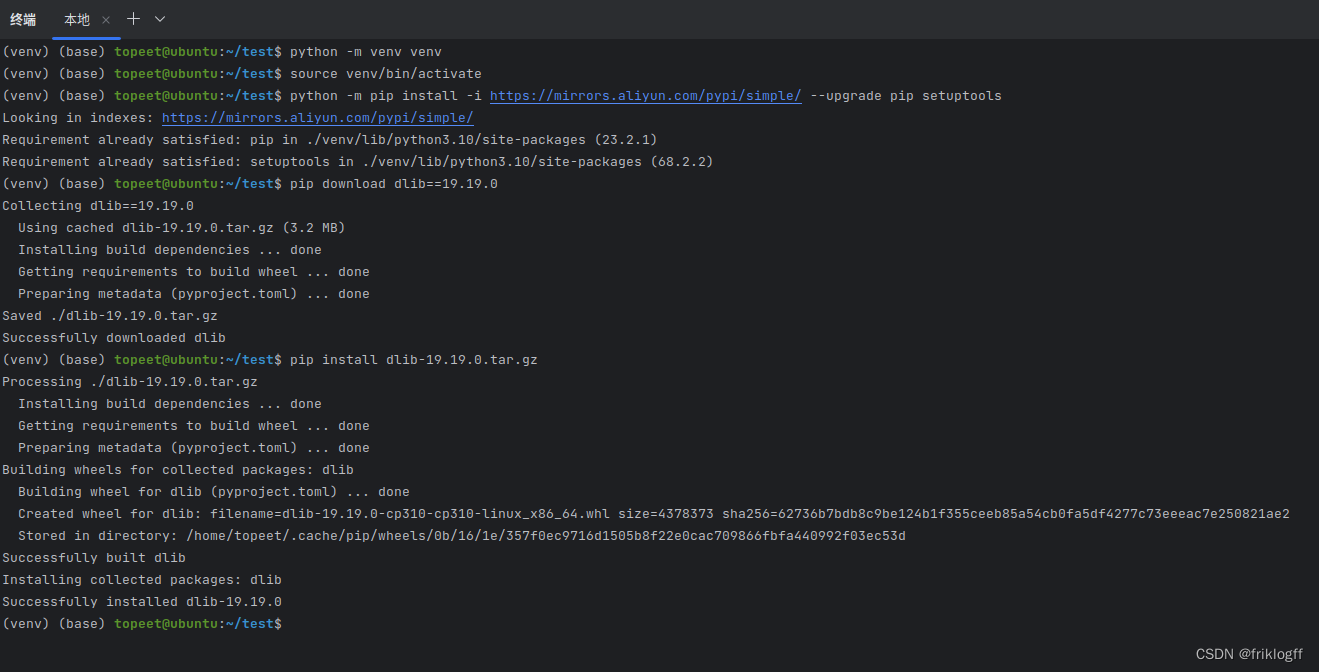
全面横扫:dlib Python API在Linux和Windows的配置方案
前言 在计算机视觉和人工智能领域,dlib是一个备受推崇的工具库。它为开发者提供了强大的图像处理、机器学习和深度学习功能。在计算机视觉项目中,配置dlib Python API是一个重要的初始步骤。本文将引导读者详细了解在Linux和Windows系统上安装和配置dli…...

30种编程语言写国庆节快乐,收藏后改改留着拜年用
文章目录 核心代码版多行代码单行代码 核心代码版 Python:print(“国庆节快乐!!!”)C:printf(“国庆节快乐!!!”);C:cout<<“国庆节快乐!!…...

SpringBoot2.7.9 配置文件加载方式
ConfigDataLocationResolver接口方法说明 isResolvable: 判断是否是需要转换的资源 resolve: 将单个ConfigDataLocation转换为ConfigDataResource集合,在激活环境配置之前加载,也就是profile文件加载之前加载 resolveProfileSpecific: 将单个ConfigDataL…...
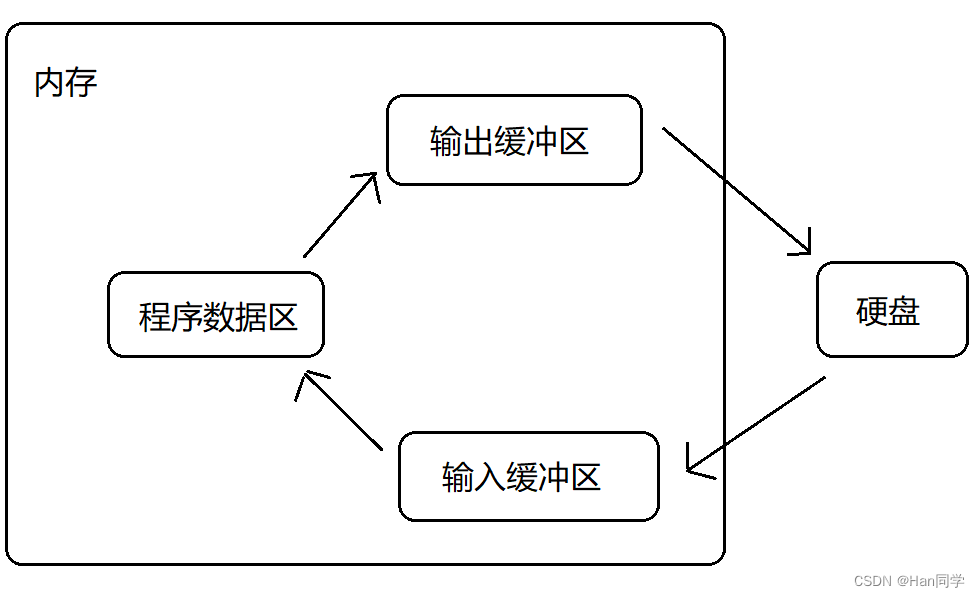
详解C语言—文件操作
目录 1. 为什么使用文件 2. 什么是文件 3. 文件的使用 文件指针 文件的打开和关闭 三个标准的输入/输出流: 4. 文件的顺序读写 对字符操作: fputc: fgetc: 练习复制整个文件: 对字符串操作:…...

IntelliJ IDEA 常用快捷键一览表
目录 1-IDEA的日常快捷键 第1组:通用型 第2组:提高编写速度(上) 第3组:提高编写速度(下) 第4组:类结构、查找和查看源码 第5组:查找、替换与关闭 第6组:…...
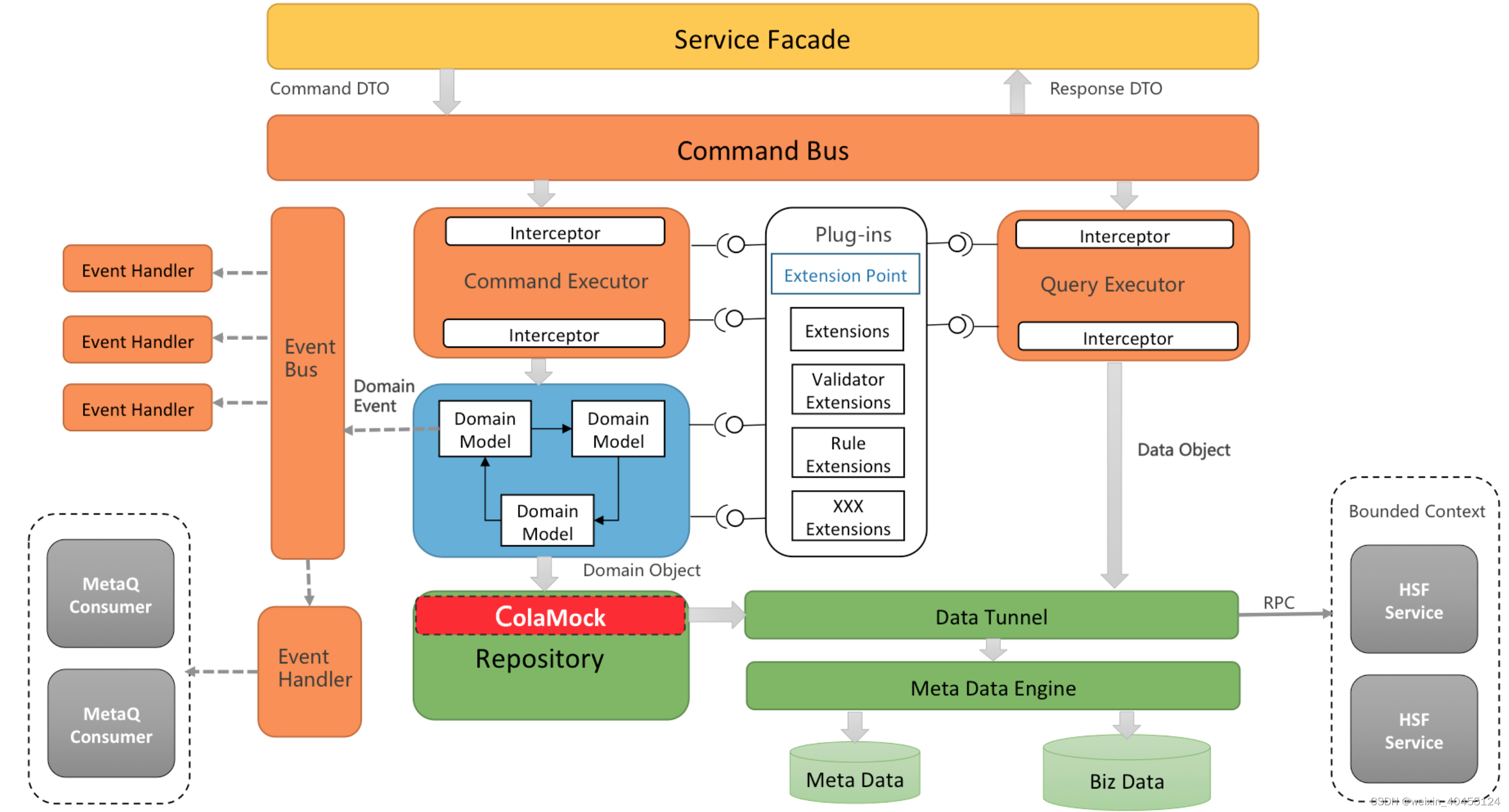
cola 架构简单记录
cola 是来自张建飞(Frank)的偏实现的技术架构,里面的业务身份和扩展点也被MEAF引用,cola本身由java 实现、但其实可以是一种企业通用的技术架构。 业务身份来源 https://blog.csdn.net/significantfrank/article/details/8578556…...

FFmpeg常用结构体分析
目录 1.AVFormatConext 2.AVInputFormat 3.AVStream 4.AVCodecContext 5.AVPacket 6.AVCodec 7.AVFrame 8.AVIOContext 9.URLProtocol 10.URLContext 1.AVFormatConext AVFormatConext是一个贯穿全局地数据结构,AVFormatConext结构包含很多信息,…...

ChatGPT 学习笔记 | 什么是 Prompt-tuning?
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 Prompt-tuning is an efficient, low-cost way of adapting an AI foundation model to new downstream tasks without retraining the model and upd…...

[红明谷CTF 2021]write_shell %09绕过过滤空格 ``执行
目录 1.正常短标签 2.短标签配合内联执行 看看代码 <?php error_reporting(0); highlight_file(__FILE__); function check($input){if(preg_match("/| |_|php|;|~|\\^|\\|eval|{|}/i",$input)){ 过滤了 木马类型的东西// if(preg_match("/| |_||php/&quo…...

JVM学习笔记
JVM学习笔记 复习之前学的内容,同时补充以下知识点:JVM的双亲委派机制、伊甸区与老年代相关知识; 双亲委派机制 首先介绍Java中的类加载器 Java中的类加载器 Bootstrap ClassLoader(启动类加载器),默认…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
