【动态规划】动态规划经典例题 力扣牛客
文章目录
- 跳台阶 BM63 简单
- 跳台阶扩展 JZ71 简单
- 打家结舍 LC198 中等
- 打家劫舍2 LC213中等
- 最长连续递增序列 LC674 简单
- 乘积最大子数组LC152 中等
- 最长递增子序列LC300 中等
- 最长重复子数组LC718
- 最长公共子串NC BM66
- 最长公共子序列LC1143 中等
- 完全平方数LC279
- 零钱兑换 LC322 中等
- 单词拆分LC139 中等
- 编辑距离LC72 困难
- 买卖股票的最佳时机LC121 简单
- 买卖股票的最佳时机2 LC122中等
- 不同路径LC62 中等
- 最小路径和LC64 中等
- 分割等和子集LC416 中等
跳台阶 BM63 简单
题目链接

代码:
public class Solution {public int jumpFloor (int number) {if(number==1||number==2)return number;// 跳一步或两步else return jumpFloor(number-1) + jumpFloor(number-2);}
}
跳台阶扩展 JZ71 简单
题目链接
描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶(n为正整数)总共有多少种跳法。

思路:
- F(n) = F(n-1)+F(n-2)+F(n-3)+…F(1)+1=F(n-1)+F(n-1) = 2*F(n-1)
- F(3)=F(2)+F(1)+1
跳上第3阶台阶,可以从第2阶、第1阶跳上去,也可以从第0阶直接1步跳上第3阶。
代码1:
public class Solution {// 当前无优化,可添加记忆数组优化时间复杂度public int jumpFloorII (int number) {if(number == 1) return 1;int count = 1;for(int i = 1;i < number;i++){count+=jumpFloorII(number-i);}return count;}
}
代码2:
public class Solution {public int jumpFloorII (int number) {if(number == 1) return 1;return 2*jumpFloorII(number-1);}
}
打家结舍 LC198 中等
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
代码:
class Solution {int[] memory;// 备忘录public int rob(int[] nums) {int len = nums.length;memory = new int[len];Arrays.fill(memory,-1);// 注意填充-1return DP(nums,0,len-1,0);}// 能打劫的范围[start,end],从i家开始选择是否打劫public int DP(int[] nums,int start,int end,int i){if(i==end)return nums[i];if(i>end)return 0;if(memory[i]!=-1)return memory[i];// 查找备忘录memory[i] = Math.max(DP(nums,start,end,i+1),// 不选nums[i]+DP(nums,start,end,i+2) // 选 隔一家在决定选择);return memory[i];}
}
打家劫舍2 LC213中等
题目链接
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:输入:nums = [1,2,3]
输出:3
思路:1 2 3 4 5围成一圈,即1与5不能同时选,则可看作是从1 2 3 4里选以及从2 3 4 5里选,取两者最大即可。
代码:
class Solution {int[] memory;// 备忘录public int rob(int[] nums) {int len = nums.length;if(len==1)return nums[0];//base case memory = new int[len];Arrays.fill(memory,-1);// 注意填充-1int r1 = DP(nums,0,len-2,0);Arrays.fill(memory,-1);// 注意填充-1int r2 = DP(nums,1,len-1,1);return Math.max(r1,r2);}// 能打劫的范围[start,end],从i家开始选择是否打劫public int DP(int[] nums,int start,int end,int i){if(i==end)return nums[i];//baseif(i>end)return 0;//baseif(memory[i]!=-1)return memory[i];// 查找备忘录memory[i] = Math.max(DP(nums,start,end,i+1),// 不选nums[i]+DP(nums,start,end,i+2) // 选 隔一家在决定选择);return memory[i];}
}
最长连续递增序列 LC674 简单
题目链接
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。代码:
class Solution {public int findLengthOfLCIS(int[] nums) {if(nums.length==1)return 1;int finalresult = 0;// 以下标 i为结尾的数组的连续递增的子序列长度为 dp[i]int[] dp = new int[nums.length]; Arrays.fill(dp,1);for(int i = 1; i < nums.length;i++){if(nums[i-1]<nums[i]){dp[i] = dp[i-1]+1;}finalresult = Math.max(finalresult, dp[i]);}return finalresult;}
}
或
class Solution {public int findLengthOfLCIS(int[] nums) {if(nums.length==1)return 1;int finalresult = 0;int temresult = 1;for(int i = 0; i < nums.length-1;i++){if(nums[i]<nums[i+1]){temresult++;}else{temresult=1;}finalresult = Math.max(finalresult,temresult);}return finalresult;}
}
乘积最大子数组LC152 中等
题目链接
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
代码:
class Solution {public int maxProduct(int[] nums) {int len = nums.length;// 因为nums中存在负数,乘积最小的值乘以-1可能变为乘积最大int[] dpmin = new int[len];// 以i结尾的乘积最小子数组的乘积int[] dpmax = new int[len];// 以i结尾的乘积最大子数组的乘积dpmin[0] = nums[0];dpmax[0] = nums[0];for(int i = 1; i < len; i++){dpmin[i] = min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i]);dpmax[i] = max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i]);}int result = dpmax[0];for(int r1:dpmax){result = result<r1?r1:result;} return result;}int max(int i,int j,int k){return Math.max(i,Math.max(j,k));}int min(int i,int j,int k){return Math.min(i,Math.min(j,k));}
}
最长递增子序列LC300 中等
题目链接
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
代码:
class Solution {public int lengthOfLIS(int[] nums) {int len = nums.length;int res = 1;// 以下标 i为结尾的数组的递增的子序列长度为 dp[i]int[] dp = new int[len];Arrays.fill(dp,1);for(int i = 0; i < len;i++){for(int j = 0;j < i;j++){if(nums[i]>nums[j]){dp[i] = Math.max(dp[i],dp[j]+1);}}}for(int i = 0; i < len;i++){res = Math.max(res,dp[i]);}return res;}
}
最长重复子数组LC718
题目链接
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
class Solution {public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length+1][nums2.length+1];int finalresult = 0;// 两个数组,就是两个forfor(int i = 1; i <= nums1.length; i++){ // 从nums1的第1个数字开始for(int j = 1; j <= nums2.length; j++){// 从nums2的第1个数字开始if(nums1[i-1]==nums2[j-1]){// 如果相同dp[i][j] = dp[i-1][j-1]+1;}finalresult = Math.max(dp[i][j],finalresult);}}return finalresult;}
}
最长公共子串NC BM66
题目链接

题目与LC718相似
public class Solution {/*** @param str1 string字符串 the string* @param str2 string字符串 the string* @return string字符串*/public String LCS (String str1, String str2) {// write code hereif(str1.length()==0||str2.length()==0)return "";int[][] dp = new int[str1.length()+1][str2.length()+1];for(int i = 0;i < str1.length();i++){dp[i][0] = 0;}for(int i = 0;i < str2.length();i++){dp[0][i] = 0;}String str = "";int maxlen = 0;for(int i = 0; i < str1.length();i++){for(int j = 0; j < str2.length();j++){if(str1.charAt(i)==str2.charAt(j)){dp[i+1][j+1] = dp[i][j]+1;if(maxlen<dp[i+1][j+1]){maxlen = dp[i+1][j+1];str = str1.substring(i-maxlen+1,i+1);}}}}return str;}
}
最长公共子序列LC1143 中等
题目链接
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
代码:
class Solution {public int longestCommonSubsequence(String text1, String text2) {int len1 = text1.length();int len2 = text2.length();int[][] dp = new int[len1+1][len2+1];for(int i = 0;i <= len1;i++){dp[i][0] = 0;}for(int i = 0;i <= len2;i++){dp[0][i] = 0;}for(int i = 1; i <= len1;i++){for(int j = 1;j <= len2;j++){if(text1.charAt(i-1)==text2.charAt(j-1)){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[len1][len2];}
}
完全平方数LC279
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
代码:
class Solution {public int numSquares(int n) {int[] dp = new int[n+1];Arrays.fill(dp,Integer.MAX_VALUE);dp[0] = 0;for(int i = 1; i <= n;i++){for(int j = 1; j*j <= i;j++){dp[i] = Math.min(dp[i],dp[i-j*j]+1);}}return dp[n];}
}
零钱兑换 LC322 中等
题目链接
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1示例 2:
输入:coins = [2], amount = 3
输出:-1示例 3:
输入:coins = [1], amount = 0
输出:0
代码:
class Solution {Map<Integer,Integer> memory = new HashMap<>();public int coinChange(int[] coins, int amount) {return DP(coins,amount);}public int DP(int[] coins,int target){if(target==0)return 0;if(target<0) return -1;// 查询备忘录if(memory.containsKey(target))return memory.get(target);int result = Integer.MAX_VALUE; // 注意此行位置for(int coin:coins){int n = DP(coins,target-coin);// 存储备忘录memory.put(target-coin,n);if(n == -1) continue; // 注意此行result = Math.min(result,n+1);}return result == Integer.MAX_VALUE?-1:result; // 注意此行}
}
单词拆分LC139 中等
题目链接
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。注意,你可以重复使用字典中的单词。示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅由小写英文字母组成
wordDict 中的所有字符串 互不相同
方法1:遍历所有单词的长度查看是否匹配
class Solution {List<String> wordDict;int[] memory ;public boolean wordBreak(String s, List<String> wordDict1) {wordDict = wordDict1;memory = new int[s.length()+1];Arrays.fill(memory,-2);return DP(s,0);}boolean DP(String s,int i){if(i==s.length()){return true;}if(i>s.length()){return false;}if(memory[i]!=-2)return memory[i]==1?true:false;for(String word:wordDict){int len = word.length();if(i+len>s.length())continue;if(s.substring(i,i+len).equals(word)){boolean r1 = DP(s,i+len);if(r1==true){memory[i]=1;return true;}}}memory[i]=0;return false;}
}
方法2:遍历所有长度查看是否匹配
class Solution {List<String> wordDict1;int[] memory;public boolean wordBreak(String s, List<String> wordDict) {wordDict1 = wordDict;memory = new int[s.length()];Arrays.fill(memory,-1);return DP(s,0);}public boolean DP(String s,int i ){if(i == s.length())return true;if(memory[i]!=-1)return memory[i]==1?true:false;for (int slen = 1; slen + i <= s.length(); slen++) {String s1 = s.substring(i,i + slen);if(wordDict1.contains(s1)){boolean b = DP(s, i + slen);if(b == true){memory[i] = 1;return true;}}}memory[i] = 0;return false;}
}
编辑距离LC72 困难
题目链接
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
思路:

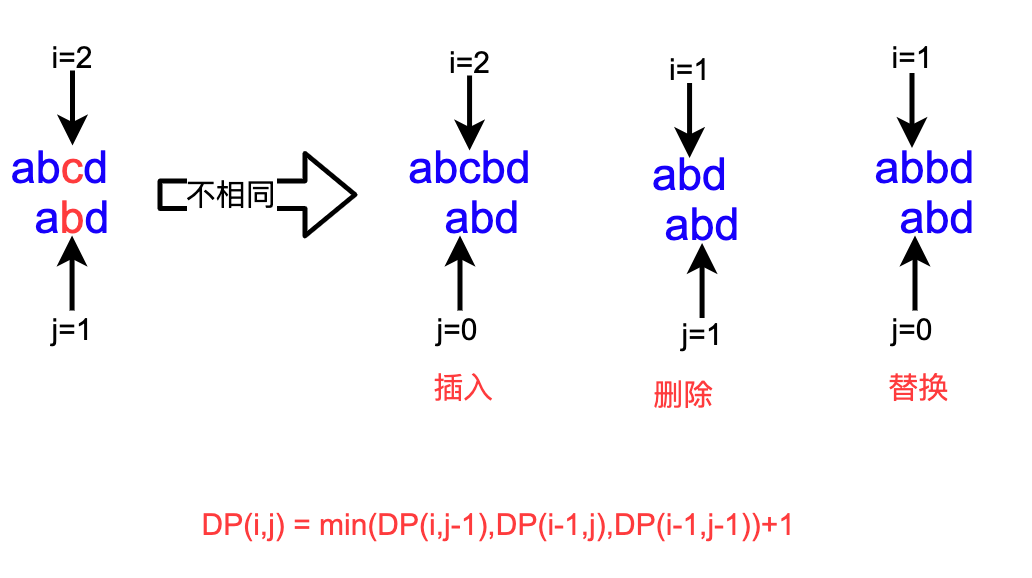
代码:
class Solution {int[][] memory;public int minDistance(String word1, String word2) {memory = new int[word1.length()][word2.length()];for(int[] m:memory){Arrays.fill(m,-1);}return DP(word1,word1.length()-1,word2,word2.length()-1);}public int DP(String w1,int i,String w2,int j){if(i == -1) return j+1;if(j == -1) return i+1;if(memory[i][j]!=-1)return memory[i][j];if(w1.charAt(i) == w2.charAt(j)){int r = DP(w1,i-1,w2,j-1);memory[i][j] = r;return r;}else{int r = min(DP(w1,i ,w2,j-1), // 插入:在w1的i的位置插入,j被匹配,j-1DP(w1,i-1,w2,j ), // 删除:对w1的i的位置删除,i-1,j未匹配DP(w1,i-1,w2,j-1) // 替换:对w1的i的位置替换,j被匹配,i替换后被匹配) + 1;memory[i][j] = r;return r;}}int min(int i,int j,int x){return Math.min(i,Math.min(j,x));}
}
买卖股票的最佳时机LC121 简单
题目链接
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
设置一个二期数组dp[][],第一维表示天数,第二维表示是否持有股票。
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][2]; // dp[i][1/0]:第i天持有1/不持有0for(int i = 0; i < prices.length;i++){if(i-1==-1){dp[i][0] = 0;dp[i][1] = -prices[0];continue;}// 未持有股票=max(昨天未持有股票,昨天持有股票今天卖出)dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);// 持有股票=max(昨天持有股票,昨天未股票今天买入)dp[i][1] = Math.max(dp[i-1][1],-prices[i]);// 只能买一次,所以第一次买时所赚利润为0-price。}return dp[prices.length-1][0];}
}
买卖股票的最佳时机2 LC122中等
题目链接
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 。示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。代码:
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][2];for(int i = 0; i < prices.length;i++){if(i-1==-1){dp[i][0] = 0;dp[i][1] = -prices[0];continue;}dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);}return dp[prices.length-1][0];}
}
不同路径LC62 中等
题目链接
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
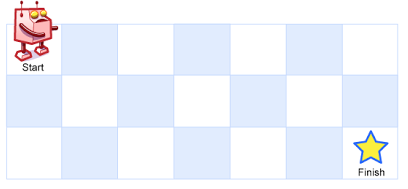
示例 1:
输入:m = 3, n = 7
输出:28示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3
输出:28示例 4:
输入:m = 3, n = 3
输出:6
代码:
class Solution {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];for(int i = 0;i < m; i++){for(int j = 0; j < n; j++){if(i==0||j==0){dp[i][j] = 1;continue;}dp[i][j] = dp[i][j-1] + dp[i-1][j];}}return dp[m-1][n-1];}
最小路径和LC64 中等
题目链接
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
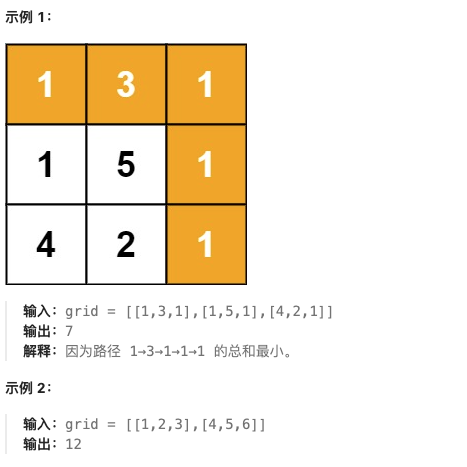
代码:
class Solution {public int minPathSum(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] dp = new int[m][n];// base case dp[0][0] = grid[0][0];for(int i = 1;i < m;i++){dp[i][0] = dp[i-1][0]+grid[i][0];}for(int i = 1;i < n;i++){dp[0][i] = dp[0][i-1]+grid[0][i];}for(int i = 1;i < m; i++){for(int j = 1; j < n; j++){dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1]) + grid[i][j];}}return dp[m-1][n-1];}
}
分割等和子集LC416 中等
题目链接
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
题解:labuladong的算法笔记
/**引用:Labuladong《算法小抄》 的第 192 页。对于这个问题,我们可以先对集合求和,得出 sum,然后把问题转化为背包问题:
给一个可装载重量为 sum / 2 的背包和 N 个物品,每个物品的重量为 nums[i]。现在让你装物品,是否存在一种装法,能够恰好将背包装满?
第一步要明确两点,「状态」和「选择」,状态就是「背包的容量」和「可选择的物品」,选择就是「装进背包」或者「不装进背包」。
dp 数组的定义:dp[i][j] = x 表示,对于前 i 个物品,当前背包的容量为 j 时,若 x 为 true,则说明可以恰好将背包装满,若 x 为 false,则说明不能恰好将背包装满。
根据 dp 数组含义,可以根据「选择」对 dp[i][j] 得到以下状态转移:
如果不把 nums[i] 算入子集,或者说你不把这第 i 个物品装入背包,那么是否能够恰好装满背包,取决于上一个状态 dp[i-1][j],继承之前的结果。
如果把 nums[i] 算入子集,或者说你把这第 i 个物品装入了背包,那么是否能够恰好装满背包,取决于状态 dp[i-1][j-nums[i-1]]*/class Solution {public boolean canPartition(int[] nums) {int sum = 0; // 数组一半的大小for(int n:nums){sum+=n;}if(sum%2!=0)return false;sum = sum/2;boolean[][] dp = new boolean[nums.length+1][sum+1];// dp[i][j] 前i个物品,j大小的包,恰好能装满即为true// base casefor(int i = 0;i < nums.length;i++){dp[i][0] = true;}for(int i = 1; i <= nums.length;i++){for(int j = 1; j <= sum; j++){if(j-nums[i-1]<0){ // 第i个物品装不下dp[i][j] = dp[i-1][j];}else{ // 能装下dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]]; // 装 or 不装}}}return dp[nums.length][sum];}
}
参考:
Labuladong
代码随想录
力扣DP题库
牛客面试必刷
相关文章:

【动态规划】动态规划经典例题 力扣牛客
文章目录 跳台阶 BM63 简单跳台阶扩展 JZ71 简单打家结舍 LC198 中等打家劫舍2 LC213中等最长连续递增序列 LC674 简单乘积最大子数组LC152 中等最长递增子序列LC300 中等最长重复子数组LC718最长公共子串NC BM66最长公共子序列LC1143 中等完全平方数LC279零钱兑换 LC322 中等单…...
统计模型----决策树
决策树 (1)决策树是一种基本分类与回归方法。它的关键在于如何构建这样一棵树。决策树的建立过程中,使用基尼系数来评估节点的纯度和划分的效果。基尼系数是用来度量一个数据集的不确定性的指标,其数值越小表示数据集的纯度越高。…...

C# List 复制之深浅拷贝
C# List 复制 之深浅拷贝 声明类 public class TestStu{public int Number{get;set; }public string Name{get;set; }}public static async Task<int> Main(string[] args){var stu1 new TestStu(){Number 1,Name "1"};var stu2 new TestStu(){Numbe…...
)
论<script> 标签可以直接写在 HTML 文件中的哪些位置?(可以将 <script> 标签直接插入到 HTML 文件的任何位置)
可以将 <script> 标签直接插入到 HTML 文件的任何位置,以在相应位置执行 JavaScript 代码。 以下是几个示例: 1.<head> 元素内部:在 <head> 元素内部放置 <script> 标签时,脚本将在页面加载过程中被下载和…...
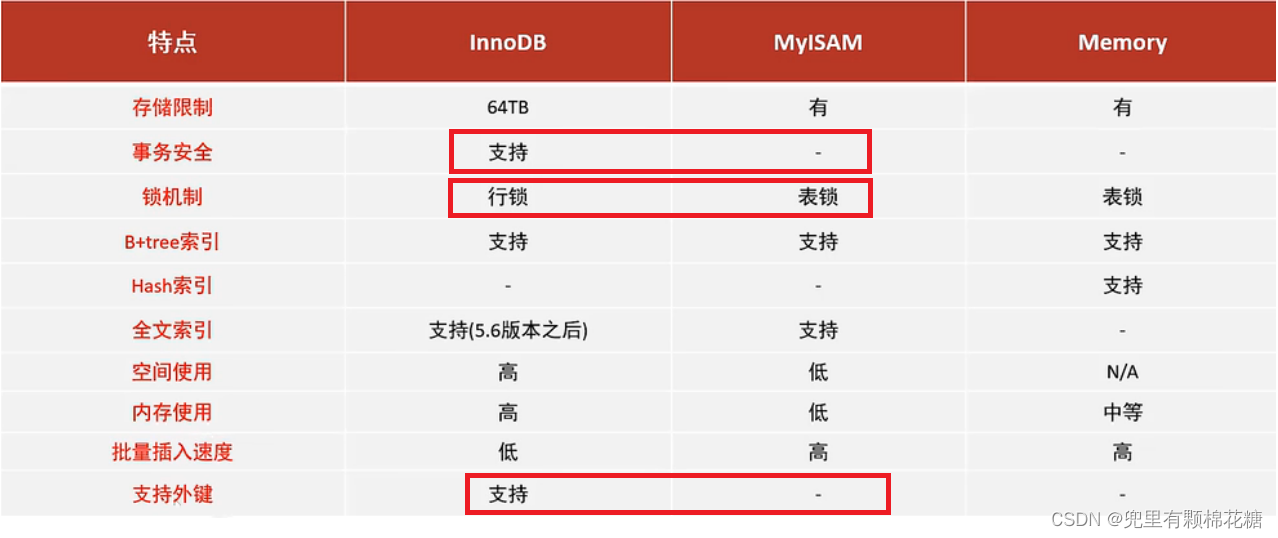
【MySQL进阶】--- 存储引擎的介绍
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【MySQL学习专栏】🎈 本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌 目录 一、什么…...
self-XSS漏洞SRC挖掘
本文由掌控安全学院 - 一朵花花酱 投稿 Markdown是一种轻量级标记语言,创始人为约翰格鲁伯(John Gruber)。它允许人们使用易读易写的纯文本格式编写文档,然后转换成有效的 XHTML(或者HTML)文档。这种语言吸…...

1859. 将句子排序
目录 一、题目 二、代码 一、题目 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 二、代码 定义了一个vector<vector<string>> v(MAX);采用const string& word : v[k] word 就会依次取得 v[k] 中的每个元素(v[k][0],…...
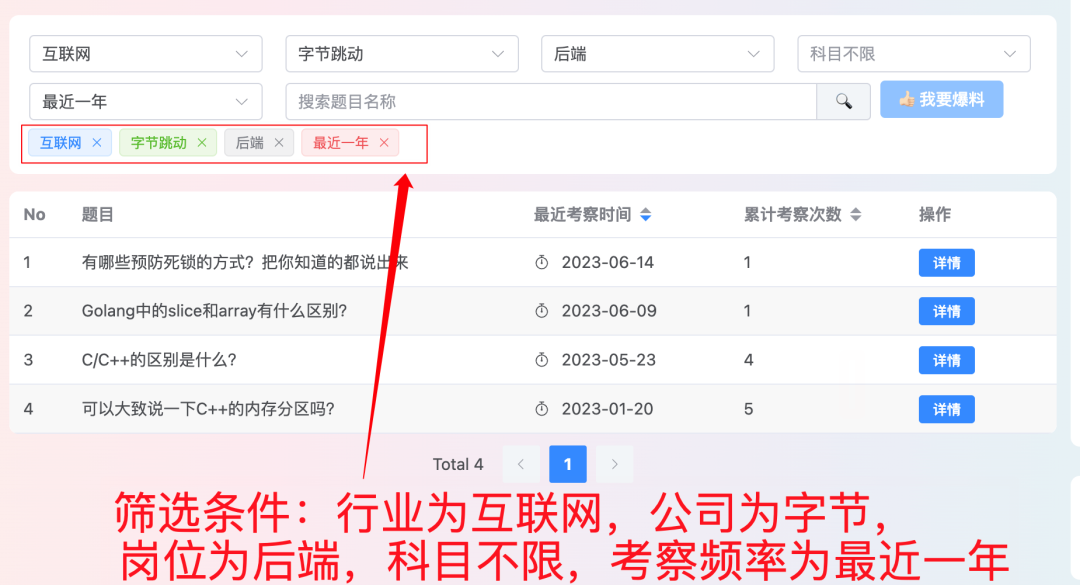
普通学校,普通背景,普通公司,不普通总结。
作者:阿秀 InterviewGuide大厂面试真题网站:https://top.interviewguide.cn 这是阿秀的第「313」篇原创 小伙伴们大家好,我是阿秀。 可能很多人点开牛客、知乎、B站,一看帖子的标题都是"某985xxxx"、"不入流211xxx…...
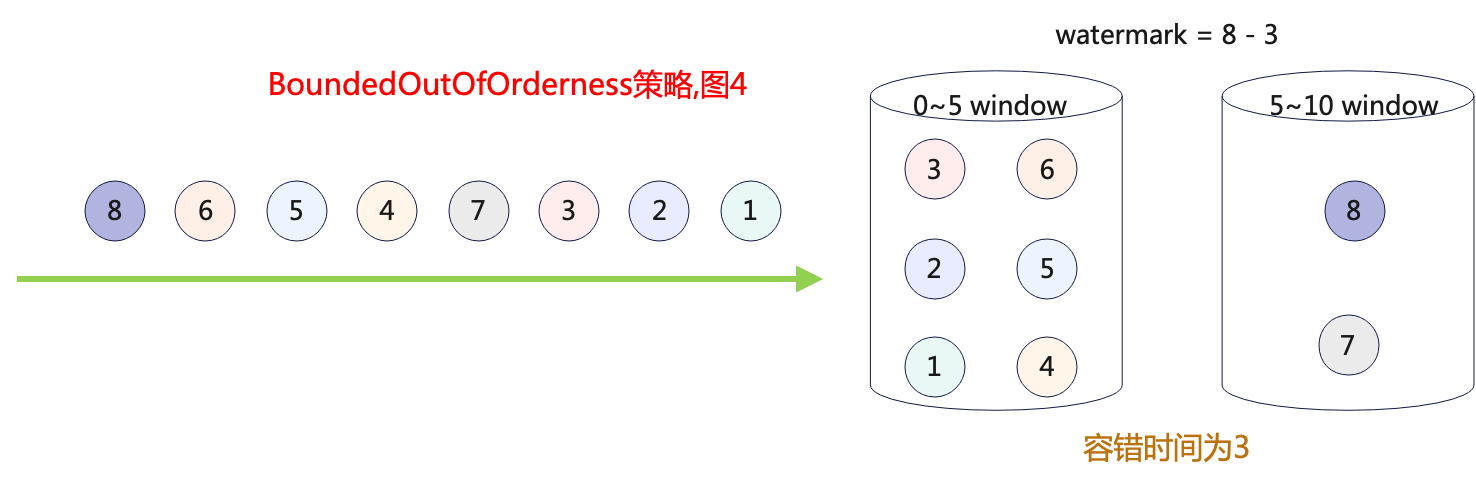
Flink之Watermark生成策略
在Flink1.12以后,watermark默认是按固定频率周期性的产生. 在Flink1.12版本以前是有两种生成策略的: AssignerWithPeriodicWatermarks周期性生成watermarkAssignerWithPunctuatedWatermarks[已过时] 按照指定标记性事件生成watermark 新版本API内置的watermark策略 单调递增的…...

提升API文档编写效率,Dash for Mac是你的不二之选
在编写和开发API文档的过程中,你是否经常遇到查找困难、管理混乱、效率低下等问题?这些都是让人头疼的问题,但现在有了Dash for Mac,一切都将变得简单而高效。 Dash for Mac是一款专为API文档编写和管理设计的工具,它…...

无人注意,新安装的 Ubuntu 23.04 不支持安装 32 位应用
导读新安装的 Ubuntu 23.04 不支持安装 32 位应用。 无人注意,新安装的 Ubuntu 23.04 不支持安装 32 位应用 有用户报告,在新安装的 Ubuntu 23.04 上从 Ubuntu 仓库安装的 Steam 客户端是不工作的。在 Ubuntu 23.04 中使用了基于 Flutter 的新安装程序…...
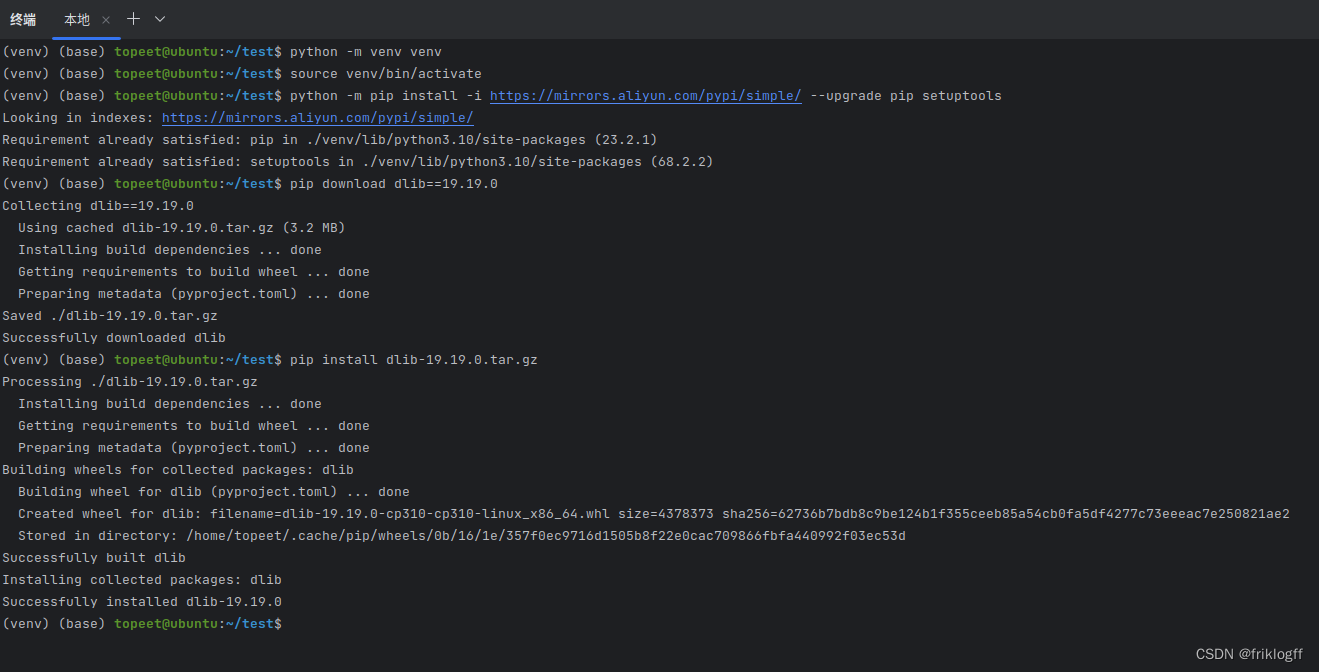
全面横扫:dlib Python API在Linux和Windows的配置方案
前言 在计算机视觉和人工智能领域,dlib是一个备受推崇的工具库。它为开发者提供了强大的图像处理、机器学习和深度学习功能。在计算机视觉项目中,配置dlib Python API是一个重要的初始步骤。本文将引导读者详细了解在Linux和Windows系统上安装和配置dli…...

30种编程语言写国庆节快乐,收藏后改改留着拜年用
文章目录 核心代码版多行代码单行代码 核心代码版 Python:print(“国庆节快乐!!!”)C:printf(“国庆节快乐!!!”);C:cout<<“国庆节快乐!!…...

SpringBoot2.7.9 配置文件加载方式
ConfigDataLocationResolver接口方法说明 isResolvable: 判断是否是需要转换的资源 resolve: 将单个ConfigDataLocation转换为ConfigDataResource集合,在激活环境配置之前加载,也就是profile文件加载之前加载 resolveProfileSpecific: 将单个ConfigDataL…...
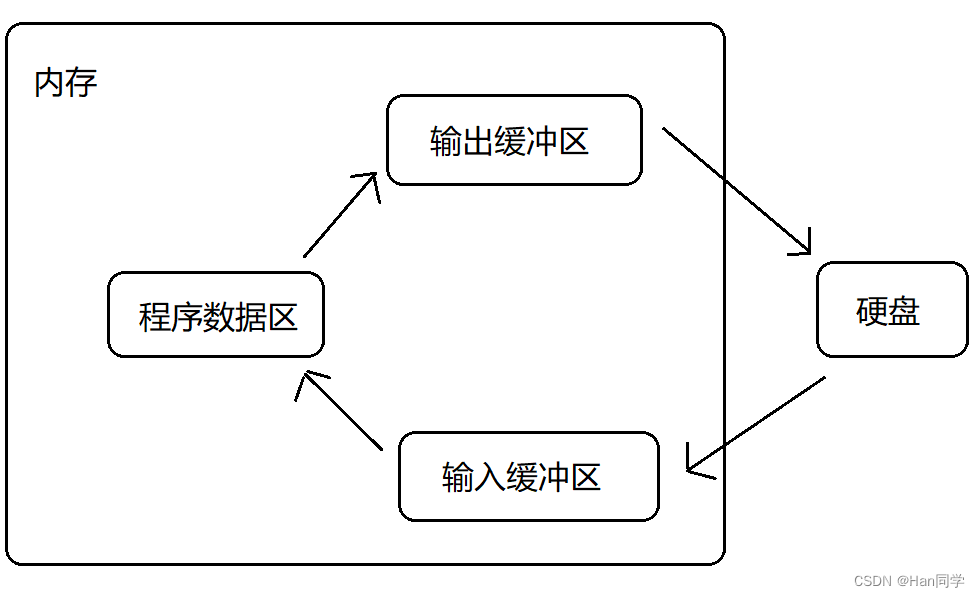
详解C语言—文件操作
目录 1. 为什么使用文件 2. 什么是文件 3. 文件的使用 文件指针 文件的打开和关闭 三个标准的输入/输出流: 4. 文件的顺序读写 对字符操作: fputc: fgetc: 练习复制整个文件: 对字符串操作:…...

IntelliJ IDEA 常用快捷键一览表
目录 1-IDEA的日常快捷键 第1组:通用型 第2组:提高编写速度(上) 第3组:提高编写速度(下) 第4组:类结构、查找和查看源码 第5组:查找、替换与关闭 第6组:…...
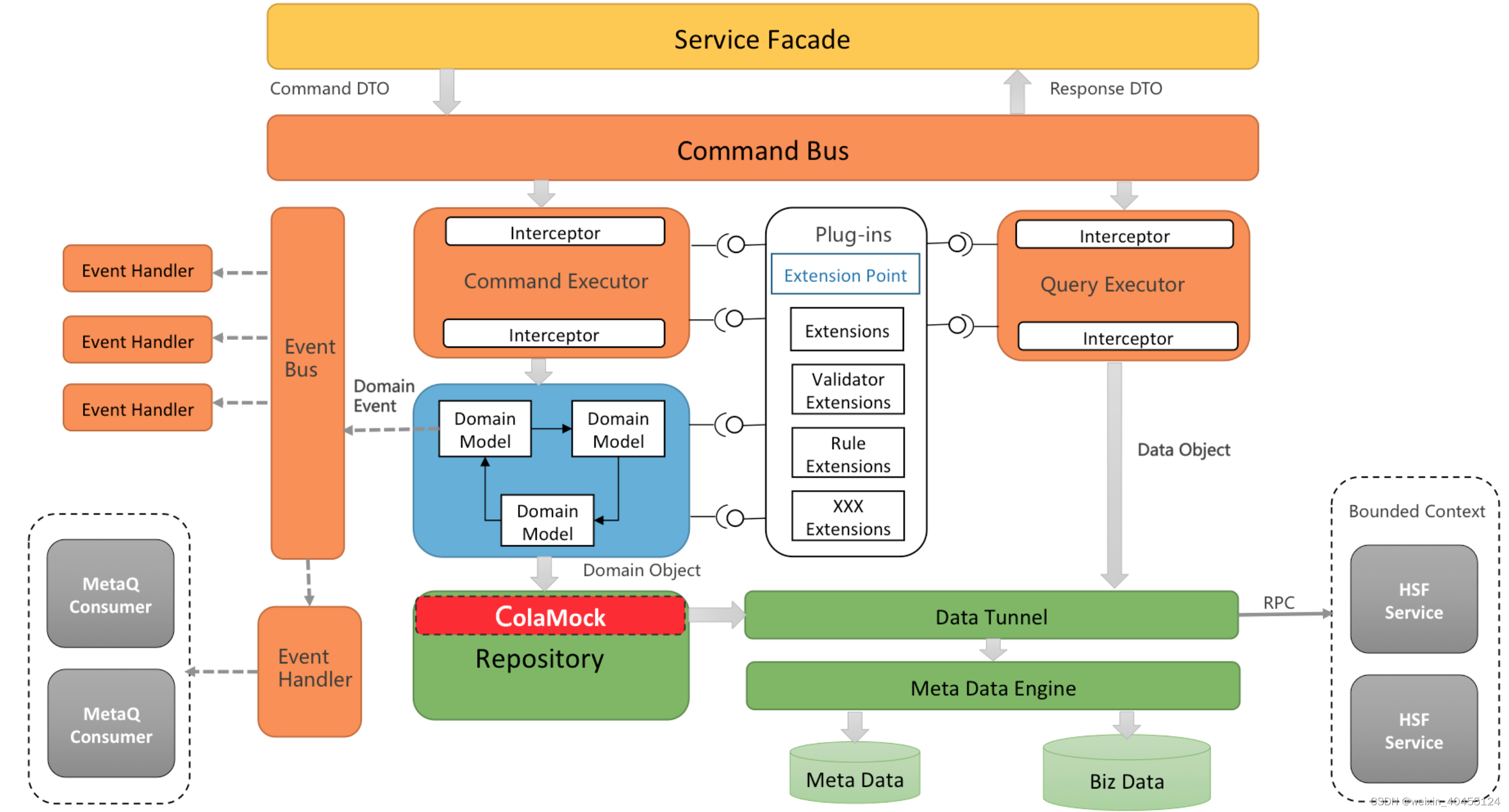
cola 架构简单记录
cola 是来自张建飞(Frank)的偏实现的技术架构,里面的业务身份和扩展点也被MEAF引用,cola本身由java 实现、但其实可以是一种企业通用的技术架构。 业务身份来源 https://blog.csdn.net/significantfrank/article/details/8578556…...

FFmpeg常用结构体分析
目录 1.AVFormatConext 2.AVInputFormat 3.AVStream 4.AVCodecContext 5.AVPacket 6.AVCodec 7.AVFrame 8.AVIOContext 9.URLProtocol 10.URLContext 1.AVFormatConext AVFormatConext是一个贯穿全局地数据结构,AVFormatConext结构包含很多信息,…...

ChatGPT 学习笔记 | 什么是 Prompt-tuning?
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 Prompt-tuning is an efficient, low-cost way of adapting an AI foundation model to new downstream tasks without retraining the model and upd…...

[红明谷CTF 2021]write_shell %09绕过过滤空格 ``执行
目录 1.正常短标签 2.短标签配合内联执行 看看代码 <?php error_reporting(0); highlight_file(__FILE__); function check($input){if(preg_match("/| |_|php|;|~|\\^|\\|eval|{|}/i",$input)){ 过滤了 木马类型的东西// if(preg_match("/| |_||php/&quo…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
